转子由于设计、结构方面的因素,以及制造安装误差等因素,实际转子的中心惯性主轴将或多或少地偏离其旋转轴线,这时称转子具有不平衡。转子不平衡在工作的时候会使机器产生振动和噪声,加速轴承等零件的磨损,对于大型转子甚至会引起重大事故,造成经济损失和人员伤亡。因此动平衡是很有必要的,动平衡的优劣程度直接影响着旋转机械设备的安全性、可靠性,寿命等。
转子根据其工作转速的大小是否远低于其一阶弯曲临界转速分为刚性转子和挠性转子两类。挠性转子的动平衡方法从理论上分为:振型平衡法和影响系数平衡法[1],以及它们的改进变形方法。当前现场动平衡中使用最多的是加试重的影响系数法,它对于挠性转子和刚性转子都适用,根据加试重的校正面的数量的不同可分为单面平衡、双面平衡,多面平衡等[2]。这些传统的动平衡的方法都需要加试重,且需多次启停转子,从而增加了动平衡的时间和成本。为了解决这个问题,P.Gniellka和G.Morton等以模态振型法为基础提出了无试重的平衡法[3],只需启停转子一次,但受到建模中轴承油膜系数准确度的影响,造成建模误差,平衡效果欠佳。浙江大学的顾晃老师提出了减少动平衡启停次数的优化方法,在已知轴承转子系统的近似影响系数的基础上,大大的降低了启停次数,但对于新设计的转子轴承系统仍需多次启停来获得其影响系数。
对于刚性转子,根据转子的动平衡理论,只需根据其转子的直径与长度的比例,采用单面加重或双面加重的方法对其进行平衡就可以达到满意的平衡效果。刚性转子加试重影响系数法由于启停次数不多,而且技术成熟,理论上容易理解,操作简单,平衡效果好,所以目前一般采用此方法进行刚性转子的动平衡[4-7]。转子动平衡的过程中,转子不平衡量的提取有传统的硬件滤波、离散傅里叶变化和互相关分析等,硬件滤波容易受到干扰,离散傅里叶变化依赖于频谱校正的好坏。随着小波分析技术的成熟,小波分析也被应用到动平衡中不平衡量的提取。在非线性转子系统不平衡量的分析中,基于全息谱的分析方法也得到了一定的应用[8]。
1 影响系数动平衡方法刚性转子的现场平衡方法主要有单面加重影响系数法、双平面加重的影响系数法等。设矢量A0、B0是在转子系统两测点测得的振动量,包含了振动的幅值和相位信息。在校正面Ⅰ加试重Q1,在相同条件下由测点测得振动为A1、B1,则平面Ⅰ加重对A、B两轴承振动的影响系数α1、β1为
| $ {\mathit{\boldsymbol{\alpha }}_1} = \frac{{{\mathit{\boldsymbol{A}}_1} - {\mathit{\boldsymbol{A}}_0}}}{{{\mathit{\boldsymbol{Q}}_1}}}, {\mathit{\boldsymbol{\beta }}_1} = \frac{{{\mathit{\boldsymbol{B}}_1} - {\mathit{\boldsymbol{B}}_0}}}{{{\mathit{\boldsymbol{Q}}_1}}}, $ | (1) |
取走试重Q1,在平面Ⅱ上加试重Q2,以同样的方式求出在平面Ⅱ上加重对两轴承振动的影响系数
| $ {\mathit{\boldsymbol{\alpha }}_2} = \frac{{{\mathit{\boldsymbol{A}}_2} - {\mathit{\boldsymbol{A}}_0}}}{{{\mathit{\boldsymbol{Q}}_2}}}, {\mathit{\boldsymbol{\beta }}_2} = \frac{{{\mathit{\boldsymbol{B}}_2} - {\mathit{\boldsymbol{B}}_0}}}{{{\mathit{\boldsymbol{Q}}_2}}}, $ | (2) |
于是,两校正平面Ⅰ、Ⅱ上实际所需的配重P1、P2可由下式线性方程组求得
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\alpha }}_1}{\mathit{\boldsymbol{P}}_1} + {\mathit{\boldsymbol{\alpha }}_2}{\mathit{\boldsymbol{P}}_2} = - {\mathit{\boldsymbol{A}}_0};\\ {\mathit{\boldsymbol{\beta }}_1}{\mathit{\boldsymbol{P}}_1} + {\mathit{\boldsymbol{\beta }}_2}{\mathit{\boldsymbol{P}}_2} = - {\mathit{\boldsymbol{B}}_0}, \end{array} \right. $ | (3) |
其模为需要加重质量的大小,相位角反映了所加重质量的位置(角度)。
在这一过程中,如何准确的求取振动的幅值和相位是校正的关键[9]。幅值和相位的求取方法主要有传统的硬件滤波、离散傅里叶变化、互相关分析和相敏分析法等[10-11],以及新近提出的离散小波分析、数字跟踪滤波法等[12-14]。
2 互相关法提取幅值和相位的基本原理相关函数描述的是2个信号(或1个信号不同时刻)之间的线性关系或相似程度。2个相同频率的周期信号,其互相关函数中保留了这2个信号的频率信息,以及2个信号的相位差信息。
将实际振动信号与标准同周期信号进行互相关即得到振动的幅值和相位。设实际振动信号为
| $ \begin{array}{l} x\left( n \right) = A\sin \left( {2{\rm{ \mathsf{ π} }}\mathit{fn + }\beta } \right) + \\ \;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^m {{\alpha _i}\sin \left( {2{\rm{ \mathsf{ π} }}{\lambda _{{i}}}n + {\theta _i}} \right) + s\left( n \right)}, \end{array} $ | (4) |
式中:A为基频振动信号的振幅;f为基频信号的频率;β基频振动信号的相位;αi其他频率振动信号的振幅;λi为对应信号的频率;θi为对应信号的相位;s(n)干扰信号[15-16]。
定义幅值为1初始相位为0的标准正、余弦函数z(n)和v(n)
| $ \left\{ \begin{array}{l} z\left( n \right) = \sin \left( {2{\rm{ \mathsf{ π} }}\mathit{fn}} \right), \\ v\left( n \right) = \cos \left( {2{\rm{ \mathsf{ π} }}\mathit{fn}} \right)。\end{array} \right. $ | (5) |
将振动信号x(n)分别与z(n)和v(n)分别做相关函数运算。根据相关函数的性质,z(n)、v(n)与其他非同频分量的互相关函数值为0,与噪音分量的相关函数值随着n的增加,很快的衰减到0,于是有
| $ \begin{array}{l} {\rm{Rxz}}\left( r \right) = \frac{1}{{N - r}}\sum\limits_{n = 0}^{N - 1 - r} {A\sin } (2{\rm{ \mathsf{ π} }}\mathit{fn }+\\ \;\;\;\;\;\;\;\;\;\;\;\beta )\sin \left[{2{\rm{ \mathsf{ π} }}\mathit{f}\left( {n + r} \right)} \right] = \\ \;\;\;\;\;\;\;\;\;\;\frac{A}{2}\cos \left( {\beta + 2{\rm{ \mathsf{ π} }}\mathit{f}r} \right);\\ {\rm{Rxv}}\left( r \right) = \frac{1}{{N - r}}\sum\limits_{n = 0}^{N - 1 - r} {A\sin } (2{\rm{ \mathsf{ π} }}\mathit{fn }+\\ \;\;\;\;\;\;\;\;\;\;\;\beta )\cos\left[{2{\rm{ \mathsf{ π} }}\mathit{f}\left( {n + r} \right)} \right] = \\ \;\;\;\;\;\;\;\;\;\;\frac{A}{2}\sin \left( {\beta + 2{\rm{ \mathsf{ π} }}\mathit{f}r} \right), \end{array} $ | (6) |
根据式(6),振动信号基频的幅值和相位分别为
| $ \begin{array}{l} A = 2\sqrt {{\rm{Rxz}}\left( 0 \right) + Rxv\left( 0 \right)} ;\\ \beta = \arctan \frac{{{\rm{Rxz}}\left( 0 \right)}}{{Rxv\left( 0 \right)}}, \beta \in [0, 2{\rm{ \mathsf{ π} }}]。\end{array} $ | (7) |
幅值和相位是通过Rxz(0)和Rxv(0)来计算的,而根据互相关的特性,信号与随机信号的相关函数,是随着点数N的增大而逐渐衰减为0的,因此Rxz(0)和Rxv(0)中包含了与随机信号的相关值,使得求取的幅值和相位存在一些偏差,影响平衡效果。
3.2 3σ准则等精度测量序列xi(i=1,2,…,n),设其样本均值为x,偏差为vi=xi-x,标准差为σ。当某值对应的偏差大于3倍标准差时,被认为是粗差,该值为坏值,予以舍弃。这一原则称为3σ准则,即
| $ \left| {{v_b}} \right| = \left| {{x_b} - \bar x} \right| > 3\sigma, $ | (8) |
式中,xb是应被舍弃的测量值,即坏值(1≤b≤n),予以舍弃,从而形成新的序列xk(k=1,2,…,m),m≤n。
对xk(k=1,2,…,m)再用3σ准则鉴别,若有坏值则舍弃,重复进行直到没有坏值为止,此时所有测量值的残差均在3σ范围内[17]。
3.3 基于3σ准则的幅值相位提取由式(6)可知,互相关之后的函数为一正弦波形函数,函数的峰值为,设互相关函数的峰值序列为Ai(i=1,2,3,…),对Ai序列运用3σ准则进行误差处理,去除坏值后求取峰值的均值,即为振动信号的准确幅值。
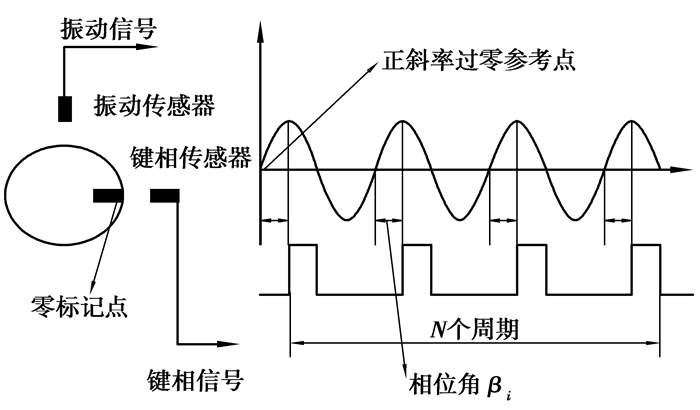
利用式(7)计算出的β值为振动信号与基频信号的相位差。基频信号是有一定宽度的脉冲信号,如图 1所示。用基准脉冲信号上升沿对振动信号截断,然后求出β值,即为正弦信号与基准信号的相位差。通过这个相位差,就可以在转子上标定出转子的不平衡量所在的角度。利用多个基准脉冲信号对振动信号进行多处截断,可以求出多个相位βi(i=1,2,3,…),这些相位值理论上相等,都是正弦信号与基准信号的相位差。最后利用3σ准则对相位序列进行误差处理,去除坏值,然后求出相位的均值,即为准确的振动信号相位角。
|
图 1 脉冲法测相法原理图 |
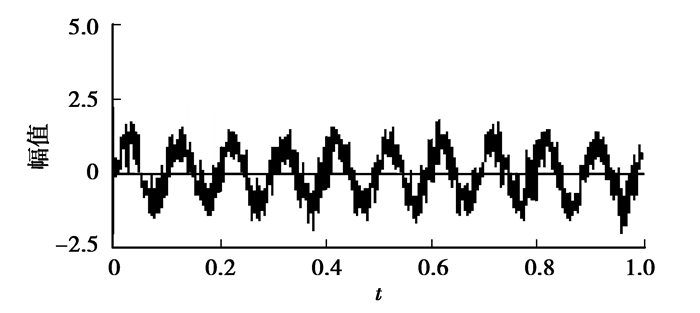
幅值为1,频率为10 Hz的正弦信号与标准差为0.4的高斯白噪声叠加,仿真信号如图 2所示。图中模拟脉冲信号的幅值为2.5,偏移量为2.5,频率为10,2信号的相位差为30°。
|
图 2 仿真信号 |
用传统的互相关技术和基于3σ的改进互相关技术分别对信号进行幅值和相位的提取,结果如表 1所示。通过仿真实验的数据可以看出,改进后的互相关技术有效的抑制了噪声分量的影响,更为准确的求取出了幅值和相位。
| 表 1 幅值相位提取对比 |
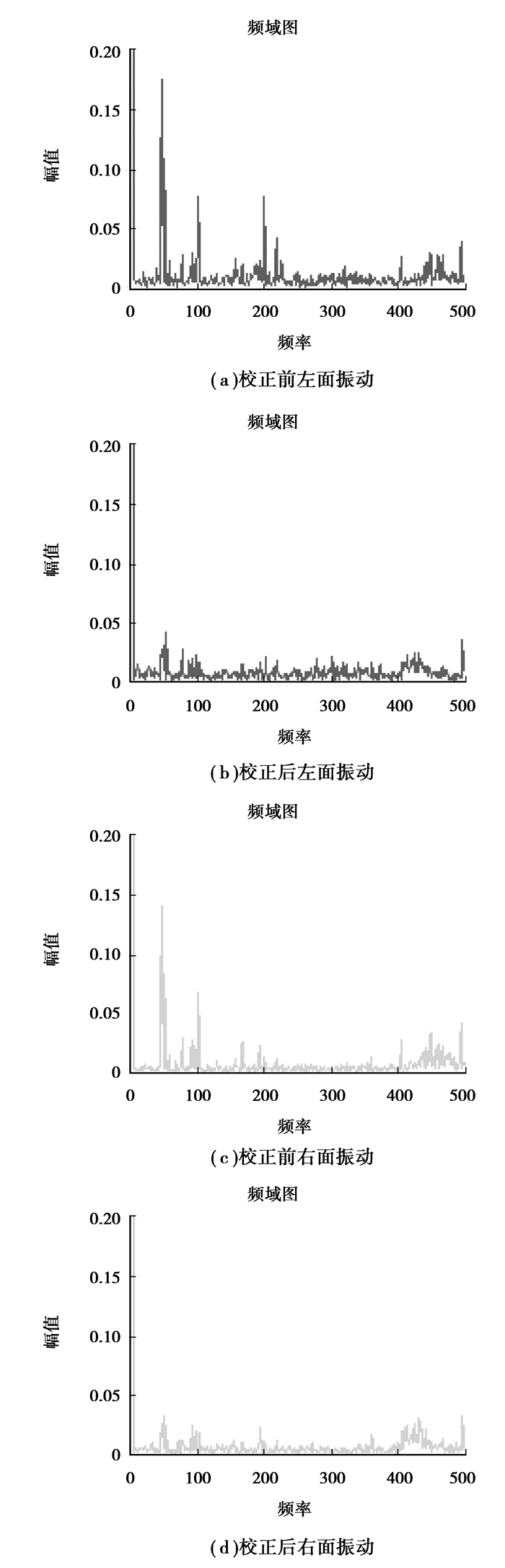
在转子动平衡实验平台上利用改进的互相关技术进行动平衡实验,如图 3所示。转子在2 700 rad/min的转速下进行双面动平衡,平衡的效果如图 4所示。改进的互相关方法准确的提取了振动信号的幅值和相位,获得了较好的平衡效果。

|
图 3 动平衡实验 |
|
图 4 校正前后振动情况 |
| 表 2 转子平衡效果 |
影响系数法因其原理清晰、操作简单等优点,广泛应用于旋转机械的动平衡分析中。而如何准确的提取信号的幅值和相位是校正的关键。
基于3σ统计处理方法的改进互相关技术可以准确的提取信号幅值和相位,减少噪声的干扰,从而更为准确的计算出转子的不平衡量。现场实验表明,该方法在转子动平衡校正中取得了很好的平衡效果。
| [1] |
黄金平, 任兴民, 邓旺群, 等.
混合平衡法的改进及其在柔性转子平衡中的应用[J]. 振动与冲击, 2008, 27(12): 47–51.
HUANG Jinping, REN Xingmin, DENG Wangqun, et al. The improvement of mixed balancing method and the application of it in flexible rotor balancing[J]. Journal of Vibration and Shoc, 2008, 27(12): 47–51. DOI:10.3969/j.issn.1000-3835.2008.12.011 (in Chinese) |
| [2] | Moon J D, Kim B S, Lee S H. Development of the active balancing device for high-speed spindle system using influence coefficients[J]. International Journal of Machine Tools&Manufacture, 2006, 9(46): 978–987. |
| [3] | El Shafei A, El Kabbany A, Younan A. Rotor balancing without trial weights[J]. Journal of Engineering for Gas Turbines and Power, 2004, 6(126): 604–609. |
| [4] | Pennacchi P, Chatterton S, Ricci R. Rotor balancing using high breakdown-point and bounded-influence estimators[J]. Mechanical systems and signal processing, 2010, 24: 860–872. DOI:10.1016/j.ymssp.2009.10.004 |
| [5] |
李斌, 张贵田, 李锋, 等.
液体火发动机涡轮泵转子的新型动平衡方法研究[J]. 振动与冲击, 2011, 30(6): 158–161.
LI Bin, ZHANG Guitian, LI Feng, et al. Novel dynamic balancing methods for turbo pump rotor in liquid rocket engine[J]. Journal of Vibration and Shock, 2011, 30(6): 158–161. (in Chinese) |
| [6] | Li C, Qin Z, Zhang Z et al. A novel design of a hard-bearing dynamic balancing machine[C]//15th International conference on Mechatronics and Machine Vision in Practice (M2VIP08). Auckland, New-Zealand:IEEE, 2008, 12(2):408-411. |
| [7] | Sethunadh R, Mohanlal P. Virtual instrument based dynamic balancing system for rockets and payloads[C]//IEEE 42nd Annual IEEE Autotestcon Conference 2007. Baltimore, MD, United states:Institute of Electrical and Electronics Engineers Inc, 2007, 9:291-296. |
| [8] |
刘淑莲, 李强, 郑水英.
基于全息谱分析的非线性转子系统不平衡量识别[J]. 机械工程学报, 2010, 46(17): 78–82.
LIU Shulian, LI Qiang, ZHENG Shuiying. Unbalance identification of nonlinear rotor system based on holospectrum analysis[J]. Journal of Mechanical Engineering, 2010, 46(17): 78–82. (in Chinese) |
| [9] | Yuan S X, Guan Z L. The identification of amplitude and phase in imbalance mass of grinding wheel[C]//6th Conference of Abrasive Technology in China. Urumqi, China:Key Engineering Materials, 2011, 487(8):391-395. |
| [10] |
秦鹏, 蔡萍.
改进经验模态分解在动平衡信号提取中的应用[J]. 仪器仪表学报, 2007, 28(1): 103–107.
QIN Peng, CAI Ping. Extracting dynamic balancing signal based on improved empirical mode decomposition[J]. Chinese Journal of Scientific Instrument, 2007, 28(1): 103–107. (in Chinese) |
| [11] |
刘健, 潘双夏, 杨克己, 等.
动平衡机用数字跟踪滤波器实现方法研究[J]. 仪器仪表学报, 2005, 26(4): 433–436.
LIU Jian, PAN Shuangxia, YANG Keji, et al. Research on digital tracking filter method of balancing machines[J]. Chinese Journal of Scientific Instrument, 2005, 26(4): 433–436. (in Chinese) |
| [12] |
郑建彬.
基于DWT和DFT的动平衡机不平衡量提取原理及实现[J]. 系统工程与电子技术, 2003, 25(4): 501–504.
ZHENG Jianbin. Principle and implementation of unbalanced signal extraction from a dynamic balancing machine based on DWT & DFT[J]. Systems Engineering and Electronic, 2003, 25(4): 501–504. (in Chinese) |
| [13] | Su H, Choi H S, Chong K T. Imbalance rotating machine balancing[C]//ICMIT 2005:Information Systems and Signal Processing, Changchun, China:Proc. of SPIE, 2005, 6041(9):20-23. |
| [14] | Wang Z S, Wang X, Luo B P. Early fault feature extraction of rotor imbalance and self-healing monitoring[C]//20094th International Conference on Innovative Computing, Information and Control. Kaohsiung, Taiwan. IEEE Computer Society, 2009(12):7-9. |
| [15] |
贺世正, 应秉斌.
基于虚拟仪器的风机动平衡测试系统的开发[J]. 风机技术, 2006(4): 33–36.
HE Shizheng, YING Bingbin. Development on test system of dynamic balance for fan based on virtual instrument[J]. Compressor, Blower & Fan Technology, 2006(4): 33–36. (in Chinese) |
| [16] |
盖建新, 马怀俭, 李延智, 等.
多通道动平衡测试系统算法[J]. 电机与控制学报, 2006, 10(4): 33–36.
GAI Jianxin, MA Huailian, LI Yanzhi, et al. Multi-channel dynamic balance test system algorithm[J]. Electric Machines And Control, 2006, 10(4): 33–36. (in Chinese) |
| [17] |
覃欣, 熊娟.
Lab VIEW数据处理中3σ准则的应用[J]. 中国测试, 2009, 35(5): 66–69.
QIN Xin, XIONG Juan. Application of 3σ rule in Lab VIEW data procession[J]. Electric Machines and Control, 2009, 35(5): 66–69. (in Chinese) |
 2013, Vol. 36
2013, Vol. 36


