2. 北京理工大学 机械与车辆学院, 北京 100081
2. School of Mechanical and Vehicle, Beijing Institute of Technology, Beijing 100081, China
汽车换档决策研究从自动变速器的出现就引起国内外科研工作者的极大兴趣,因为换档决策与汽车的动力性、经济性、舒适性、发动机寿命、排放性能和换档平顺性等息息相关,是车辆自动变速理论的核心内容[1]。此外,俄亥俄州立大学Pierluigi Pisu和Giorgio Rizzoni通过仿真表明,在基于规则和H∞的混合动力汽车能量管理策略中对换档点的选择非常敏感[2]。目前,大部分混合动力的研究成果通常是将换档决策融合进整车能量管理中进行决策[3],并且大部分都采用与传统车辆类似的双参数换档规律,例如选择油门开度(或驾驶员驱动功率需求)和车速作为控制参数[4],也有一部分采用单参数换档规律[5]。
韩国国立首尔大学Han-Sang Cho基于油门和车速的双参数换档理论提出通过最大化混合动力传动系统效率来确定换档点[6]。古艳春按照储备加速能力最大和综合燃油消耗最小原则,分别确定了混合动力汽车在混合驱动模式下的动力性和经济性换档规律[7]。吉林大学王伟华根据并联混合动力汽车中电机和电池的运行特点,提出了以保证车辆动力性为前提的混合动力汽车经济性三参数换档规律[8]。上海交通大学周国清在传统汽车双参数动力性换档规律的基础上,增加表征ISG电机工作状况的电池SOC,分别进行混合动力汽车的动力性和经济性研究[9]。
上述换档决策理论依据多从传统车辆换档决策理论出发,未脱离传统工程理论的研究框架,因此有必要开展更加深入的最优化研究。动态规划方法是把原来动态系统的最优控制问题,考虑成按动态系统初始状态参数化了的一族控制系统的最优化控制问题[10],非常适合混合动力系统以参数化行驶工况为输入的最优控制,并且该方法在混合动力能量流管理中获得了广泛应用[11-14]。
笔者在MATLAB/Simulink环境下建立了某混合动力客车的整车模型,以等效燃油消耗、发动机污染物排放和换档频繁程度为指标函数,以车速、功率流分配系数和电池SOC值为状态变量,以变速器档位为决策变量,以发动机、电机、电池和变速器的物理特性为约束,建立了混合动力客车状态转移方程,并设计了针对该混合动力系统的动态规划求解算法。通过仿真和实车试验分别对传统双参数和基于动态规划算法的换档决策进行了对比分析。
1 混合动力客车简化模型为了保证各子系统的高度模块化,提高仿真平台通用性,在MATLAB/Simulink环境下建立整车仿真模型。仿真平台示意图见图 1,图中上层部分为机械功率传递,下层为控制系统及电气功率部分,其中驱动电机转子轴与变速器输入轴通过花键进行同轴转矩耦合。整车整备质量为13 100 kg,整车满载质量为18 000 kg,其他混合动力传动系统相关参数如表 1所示。
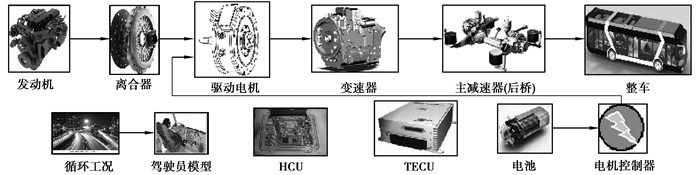
|
图 1 混合动力客车仿真平台示意图 |
| 表 1 混合动力系统主要部件及参数 |
对动态规划算法而言,上述传统模型过于复杂,容易导致维数灾难,因此有必要在建模过程中对混合动力系统的各个模块的模型进行合理简化。
1) 发动机模型。基于发动机的准静态假设忽略发动机的动态特性[15],那么发动机的燃油消耗率
2) 变速器模型。简化后变速器模型忽略各档位下不同转速和不同转矩输入时的功率损失,变速器档位模型直接由式(1)描述。各档位传动比ig, t表示如下
| $ {i_{{\rm{g, t}}}} = {i_{\rm{G}}}\left( {{N_{{\rm{g, act}}}}} \right), $ | (1) |
式中:iG为各档位下传动比表;Ng, act为变速器当前档位。
3) 电机模型。电机可输出转矩Telm受到的影响因素较多,需要综合考虑混合动力控制器对电机的转矩需求Telm, req、电机当前转速下最大允许驱动和制动转矩Telm, dis、Telm, chg以及动力电池在放电和充电时允许的电机最大转矩Tbat, dis、Tbat, chg来确定电机最终可输出转矩Telm,
| $ {\mathit{\boldsymbol{T}}_{{\rm{elm}}}} = \left\{ \begin{array}{l} \min \left( {{\mathit{\boldsymbol{T}}_{{\rm{elm, rep}}}}\mathit{\boldsymbol{, }}{\mathit{\boldsymbol{T}}_{{\rm{elm, dis}}}}\mathit{\boldsymbol{, }}{\mathit{\boldsymbol{T}}_{{\rm{bat, dis}}}}} \right), {\rm{if}}\;\;{\mathit{\boldsymbol{T}}_{{\rm{elm, rep}}}} > 0, \\ \max \left( {{\mathit{\boldsymbol{T}}_{{\rm{elm, rep}}}}\mathit{\boldsymbol{, }}{\mathit{\boldsymbol{T}}_{{\rm{elm, chg}}}}\mathit{\boldsymbol{, }}{\mathit{\boldsymbol{T}}_{{\rm{bat, chg}}}}} \right), {\rm{if}}\;\;{\mathit{\boldsymbol{T}}_{{\rm{elm, rep}}}} < 0, \end{array} \right. $ | (2) |
4) 电池模型。忽略电池的热力学因素,不考虑温度变化对电池内阻、内部电容的影响,将电池Thrvenin模型简化成静态等效电路,如图 2所示。图中R0为电池内部阻抗,Ω;R1为电池响应的动力学系数;Voc为电池开路电压。
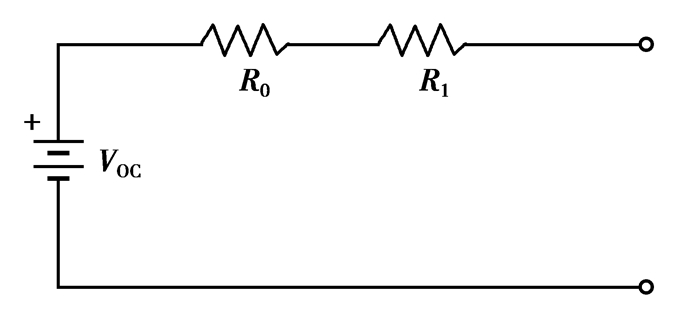
|
图 2 电池静态简化电路 |
描述电池状态的唯一变量电池SOC变化如下
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{SO}}{{\rm{C}}_{k + 1}} = {\rm{SO}}{{\rm{C}}_k} - \\ \frac{{{V_{{\rm{oc}}}} - \sqrt {V_{{\rm{oc}}}^2 - 4\left( {{R_0} + {R_1}} \right) \cdot {\mathit{\boldsymbol{T}}_{{\rm{elm}}}} \cdot {\omega _{{\rm{elm}}}} \cdot \eta _{{\rm{overall}}}^{ - {\mathop{\rm sgn}} \left( {{\mathit{\boldsymbol{T}}_{{\rm{elm}}}}} \right)}} }}{{2\left( {{R_0} + {R_1}} \right) \cdot {Q_0}}}, \end{array} $ | (3) |
式中:ηoverall为电机至电池的能量转换效率;Q0为电池最大荷电量,kW·h;ωelm为电机转子轴转速, rad/s。
5) 车辆纵向动力学模型。车辆纵向动力学模型简化成点质量模型,车速的状态方程
| $ {v_{{\rm{vel, }}\mathit{k}{\rm{ + 1}}}} = {v_{{\rm{vel, }}\mathit{k}}} + \frac{1}{{\delta {m_{\rm{v}}}}}\left( {\frac{{{\mathit{\boldsymbol{T}}_{{\rm{wheel}}}}}}{{{r_{{\rm{wheel}}}}}} - \frac{{{v_{{\rm{vel, }}\mathit{k}}}}}{{\left| {{v_{{\rm{vel, }}\mathit{k}}}} \right|}}{F_\psi }} \right) $ | (4) |
式中:vvel, k为第k决策阶段时车速,m/s;mv为整车装备质量,kg;Twheel为车轮所受净转矩,即驱动和机械制动转矩的代数和,N·m;rwheel为车轮滚动半径,m;δ为旋转质量系数;Fψ为汽车行驶阻力,N。
2 换档决策目标泛函的建立混合动力传动系统状态模型在离散时间域可以由式(5)表述
| $ {\mathit{\boldsymbol{X}}_{k + 1}} = f\left( {{\mathit{\boldsymbol{X}}_k}, {\mathit{\boldsymbol{U}}_\mathit{k}}} \right), $ | (5) |
式中:Xk为混合动力系统状态向量;Uk为换档决策向量;k为时间序列。
为了使换档控制器的目标档位命令Uk在下一个命令Uk+1输出之前可以在换档执行系统中很好地执行,初步设定以1s为控制周期。最优化的目标就是要寻找Uk,使得目标泛函最小,目标泛函由等效燃油消耗函数和排放函数相加获得。
| $ \begin{array}{l} J = \sum\limits_{k = 0}^{N - 1} {L\left( {{\mathit{\boldsymbol{X}}_k}, {\mathit{\boldsymbol{U}}_\mathit{k}}} \right)} = \sum\limits_{k = 0}^{N - 1} {\left( {1 - K} \right){m_{{\rm{f, eqv}}}}} + \\ \;\;\;\;\;\;K\left( {A \cdot {\rm{N}}{{\rm{O}}_{{\mathit{\boldsymbol{X}}_k}}} + B \cdot {\rm{SOOT}}{_{{\mathit{\boldsymbol{X}}_k}}}} \right), \end{array} $ | (6) |
式中:等效燃油消耗量mf, eqv定义参考式(7);N为循环工况持续时间;L为瞬时目标值,包括等效燃油消耗量和发动机的氮氧化物、烟度;K为等效燃油经济性和排放性平衡权重因子,K∈[0, 1]。对于只以燃油消耗量为目标泛函的优化过程,平衡排放权重因子K=0, A和B为各污染物排放权重。
| $ \left\{ \begin{array}{l} {m_{{\rm{f, }}\mathit{i}{\rm{, eqv}}}} = {P_{{\rm{ice}}}}{{\dot m}_{{\rm{f, ice}}}} + {P_{{\rm{elm}}}}{{\dot m}_{{\rm{f, elm}}}};\\ {{\dot m}_{{\rm{f, elm}}}} = \frac{{\gamma \left( {{P_{{\rm{elm}}}}} \right)}}{{\eta {'_{\rm{elm, dis}}}\left( {{P_{{\rm{elm}}}}} \right) \cdot {\eta _{{\rm{bat, dis}}}} \cdot {\eta _{{\rm{bat, chg}}}} \cdot {\eta _{{\rm{elm, chg}}}} \cdot {\eta _{{\rm{trans}}}} \cdot {\eta _{{\rm{ice}}}}\left( {{P_{{\rm{elm}}}}} \right)}}\\ \;\;\;\;\;\;\;\;\frac{1}{{{H_{{\rm{LHV}}}}}};\\ \;\;\;\;\;\;\;\gamma \left( {{P_{{\rm{elm}}}}} \right) = s\left( t \right)\frac{{1 + {\rm{sign}}\left( {{P_{{\rm{elm}}}}} \right)}}{2}, \end{array} \right. $ | (7) |
式中:
当然在优化过程中,需要运用边界型不等式对发动机、电机、电池和变速器的状态进行约束,保证各部件工作在允许范围。
| $ \begin{array}{l} {\omega _{{\rm{ice}}\_\min }} \le {\omega _{{\rm{ice}}, k}} \le {\omega _{i{\rm{ce}}\_\max }};\\ {T_{{\rm{ice}}\_\min }}\left( {{\omega _{{\rm{ice}}, k}}} \right) \le {T_{{\rm{ice}}, \mathit{k}}} \le {T_{{\rm{ice}}\_\max }}\left( {{\omega _{{\rm{ice}}, k}}} \right);\\ {T_{\mathit{elm}\_\min }}\left( {{\omega _{\rm{elm}, k}}, {\rm{SO}}{{\rm{C}}_k}} \right) \le {T_{\rm{elm}, \mathit{k}}} \le {T_{\rm{elm}\_\max }}\left( {{\omega _{\rm{elm}, k}}, {\rm{SO}}{{\rm{C}}_k}} \right);\\ {\rm{SO}}{{\rm{C}}_{\min }} \le {\rm{SO}}{{\rm{C}}_k} \le {\rm{SO}}{{\rm{C}}_{\max }};\\ {N_{{\rm{g, min}}}} \le {N_{{\rm{g, }}\mathit{act}}} \le {N_{{\rm{g, max}}}}。\end{array} $ | (8) |
式中:ωice, k,Tice, k分别为第k决策阶段发动机转速及其输出转矩,rad/s,N·m;ωice_min,ωice_max分别为发动怠速转速和最高转速,rad/s;Tice_min(ωice, k)、Tice_max(ωice, k)分别为发动机当前转速下的摩擦转矩和所能输出的最大转矩,N·m;Telm, k为第k决策阶段电机输出转矩,N·m;Telm_min(ωelm, k, SOCk)、Telm_max(ωelm, k, SOCk)分别为电机在当前转速和电池SOC限制下所能提供的最大输入和输出转矩,N·m;SOCk为第k决策阶段电池荷电状态;SOCmin、SOCmax为电池允许工作区间,取值0.2~0.8;Ng, min、Ng, max分别为变速器最低档和最高档位。
此外,为了对频繁换档现象进行约束,增加了换档惩罚函数。
| $ {S_k} = \varphi \left| {{N_{{\rm{g}}, k + 1}} - {N_{{\rm{g}}, k}}} \right|, $ | (9) |
式中:ϕ为惩罚因子,其值越大意味着档位更换的代价越大,反之则倾向于档位更换;Ng, k、Ng, k+1分别为当前档和期望档位。式(6)可表达为
| $ \begin{array}{l} J = \sum\limits_{k = 0}^{N - 1} {L\left( {{X_k}, {\mathit{U}_\mathit{k}}} \right)} = \sum\limits_{k = 0}^{N - 1} {\left( {1 - K} \right){m_{{\rm{f, eqv}}}}} + \\ \;\;\;\;\;\;\;\;K\left( {A \cdot {\rm{N}}{{\rm{O}}_{{\mathit{X}_\mathit{k}}}} + B \cdot {\rm{SOO}}{{\rm{T}}_{{\mathit{X}_\mathit{k}}}}} \right) + {S_k}。\end{array} $ | (10) |
由于混合动力传动系统是连续非线性系统,直接通过解析法或数值方法对余留目标泛函进行求解是十分费时的。典型地,将动态规划转化为有限次计算问题的一般解法是对状态空间进行离散化,并且极小化成有限个状态进行的[16]。混合动力传动系统的状态矢量空间Xk由正向功率流分配系数PSRk和电池SOCk组成,
| $ {X_k} = [\rm{PSR}{_\mathit{k}}, \rm{SOC}{_\mathit{k}}]', $ | (11) |
各分量离散化如下
| $ {\rm{PSR}}{_\mathit{k}} = \{ 0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.8, 1\}, $ | (12) |
| $ {\rm{SOC}}{_\mathit{k}} = \{ 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8\}, $ | (13) |
其中功率流分配系数PSR定义如下
| $ {\rm{PSR}} = \frac{{{P_{{\rm{ice}}}}}}{{{{\mathop{\rm P}\nolimits} _{{\rm{rep}}}}}}, $ | (14) |
式中:Pice为发动机功率,kW;Preq为驾驶员功率需求,kW。
控制量μi*即为期望目标档位Ng, desired
| $ {N_{\rm{g, desired}}} \in \{ 1, 2, 3, 4, 5\}, $ | (15) |
将Bellman最优性原理在整个优化阶段进行应用,则有
第N-1步
| $ J_{N - 1}^ * \left( {{X_{N - 1}}} \right) = \mathop {\min }\limits_{u_{N - 1}^*} [L\left( {{X_{N-1}}, {U_{N-1}}} \right)], $ | (16) |
第k步,0≤k<N-1,
| $ J_k^*\left( {{X_k}} \right) = \mathop {\min }\limits_{u_k^*} [\mathit{L}\left( {{\mathit{\boldsymbol{X}}_k}, {\mathit{\boldsymbol{U}}_k}} \right) + {\mathit{J}^*}_{\mathit{k} + 1}\left( {{\mathit{\boldsymbol{X}}_{\mathit{k}{\rm{ + 1}}}}} \right)], $ | (17) |
式中:Jk*(Xk)为从步骤k至最终阶段的最小代价函数值。
详细的目标泛函由式(12)、(13)、(15)组成的离散化状态空间根据决策量插值获得。为了对递推式(17)进行数值求解,在每一步的优化搜索过程,目标泛函的评估值都位于离散状态空间的网格点处,如果下一个状态Xk+1不在离散网格处,此时需要对该目标泛函值进行线性插值。
通过对递推式(17)的反向求解将可以得到全局最优策略,当然每一步的优化过程都受到式(8)的约束。尽管对模型进行了简化并制定了量化网格,但若仿真时间为t则需进行(Ng, max)t次目标泛函计算,将不可避免地导致计算灾难。笔者采用两种途径来加速优化搜索。对于已知车辆,其驱动轮处功率Pwheel, req和转矩Twheel, req可运用式(4),根据循环行驶工况的速度属性导出,将该过程融入输入状态更新网格,车辆模型由车轮需求转矩Twheel, req和转速ωwheel, req代替。另一种途径是使用MATLAB®fmincon.m函数预先根据功率流分配策略对各换档决策树下的目标泛函进行计算,绘制出可供实时查询的表格。具体的动态规划流程如图 3所示。图中对于给定循环工况,首先按第一种途径加速优化搜索,将时间车速转换为时间功率图(放大图中数字标号代表时间片段)。由基于有限状态机的功率流分配策略确定发动机和电机各自的功率输出,fmincon根据目标泛函寻找到最优档位决策,确定变速器输入轴转速,之后分别计算出发动机和电机的具体转矩命令,完成混合动力的功率流传递,并对混合动力系统状态空间进行更新。
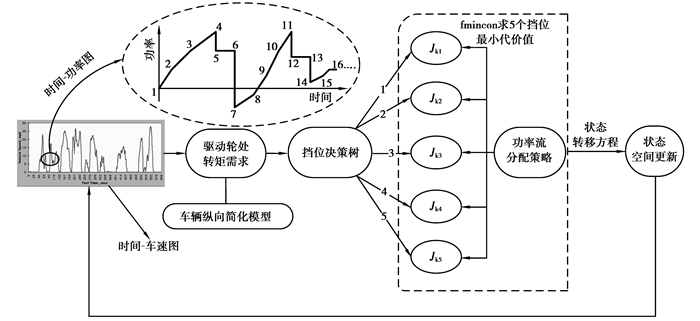
|
图 3 动态规划流程示意图 |
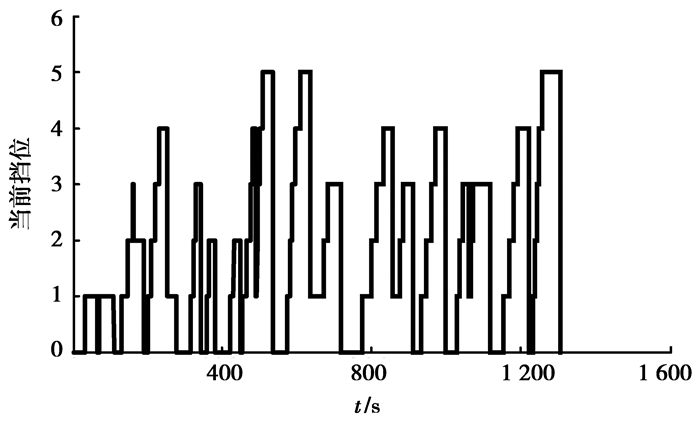
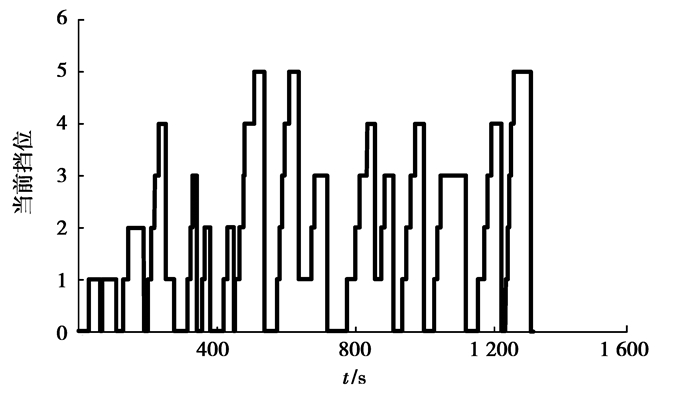
笔者以中国汽车技术中心承担的“863”重大专项“典型城市车辆实际行驶工况的研究”课题成果-中国典型城市公交客车行驶工况[17]为动态规划算法的参数化工况输入。根据上述动态规划算法获得该工况下的最优换档决策序列。通过对式(9)循环换档处罚因子进行调整并且不考虑排放代价的前提下得到了不同换档决策序列。图 4、图 5和图 6分别为不同值下换档决策序列。当ϕ=2.5时获得了该工况下全局目标泛函最小且换档次数也最少的最优换档决策序列。
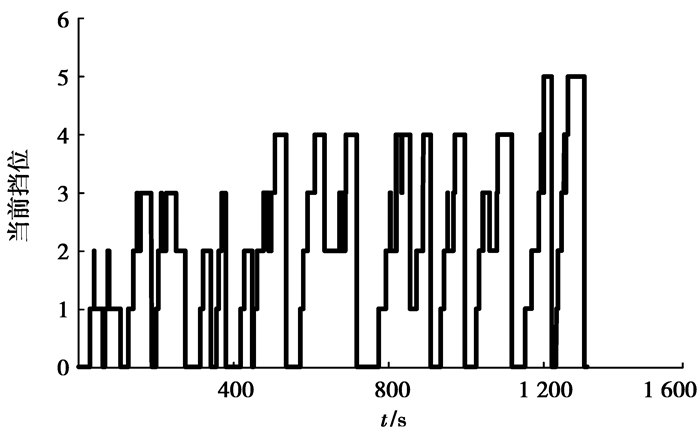
|
图 4 时的换档决策序列 |
|
图 5 时的换档决策序列 |
|
图 6 时的换档决策序列 |
将上述动态规划算法生成的随行驶工况时间变化的最优换档决策序列,应用在图 1中使用传统建模方法建立的整车仿真平台。比较仿真平台中仿真结果与动态规划算法获得的燃油消耗量,两者偏差在范围内,因此上述方法很好地避免了由于动态规划算法需要而对模型简化造成的影响,增加了动态规划结果的可信度。
在进行动态规划时,混合动力系统的状态空间中需要进行初始设置的只有电池SOC,因此仿真平台只将初始SOC设置为±0.5。接下来分别对燃油经济性和综合考虑燃油经济及排放的仿真结果进行分析。
4.1 燃油经济性结果将式(10)中平衡因子设置为K=0,则只根据燃油经济性进行动态规划,初始电池SOC设置为50%,换档循环惩罚因子设置为ϕ=2.5,所获得最优换档决策序列即图 6。
为了对不同换档决策效果进行综合评价,根据欧洲排放法规对各项评价指标进行了加权计算以获得整体性能指标Indexmulti(由于发动机制造商提供的排放数据是在台架试验中获得,可能与实际应用中存在差异,其中烟度与颗粒物成正比例关系,即烟度大时颗粒排放也大[18])。
| $ {\rm{Inde}}{{\rm{x}}_{{\rm{multi}}}} = {\rm{Fuel + 0}}{\rm{.1N}}{{\rm{O}}_\mathit{x}} + 0.1{\rm{SOOT + 0}}{\rm{.3shif}}{{\rm{t}}_{{\rm{freq}}}} $ | (18) |
式中:Fuel为百公里燃油消耗量,L/100 km;NOx为百公里氮氧化物排放量,g/100 km;SOOT为百公里烟度排放量,g/100 km;shift为每公里平均换档次数,无量纲。
基于动态规划的换档决策与采用传统双参数换档决策相比较,优化效果非常明显,综合性能提高了25.7%,见表 2,并且平均换档频率减少了35%以上。
| 表 2 中国典型城市公交循环工况仿真结果对比 |
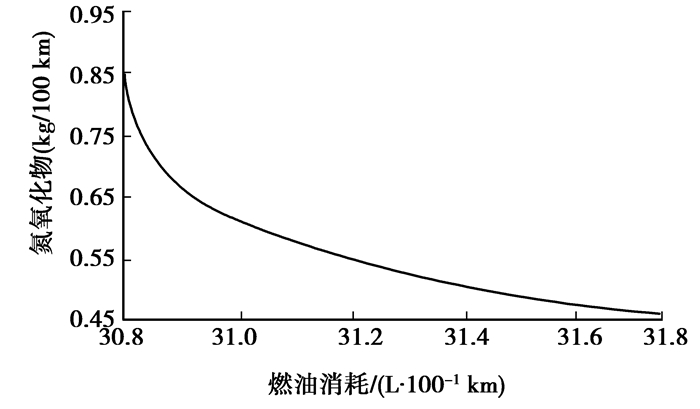
尽管目前单纯依靠对柴油机工作点和负荷进行优化已经远远不能满足日益严格的排放法规(目前排放性能的提升主要集中在后处理方面,如选择性还原催化(SRC)、颗粒捕捉等),但柴油机工作点作为排放的源头还是有一定的提升空间。将式(6)中平衡因子K从0开始以等间隔步长0.01增加至1进行仿真,图 7是燃油消耗量与NOx排放量平衡曲线,从图中可以看到两者呈现出互斥关系,为了降低排放势必增加燃油消耗量,反之亦然。
|
图 7 燃油消耗量与NOx物排放量平衡曲线 |
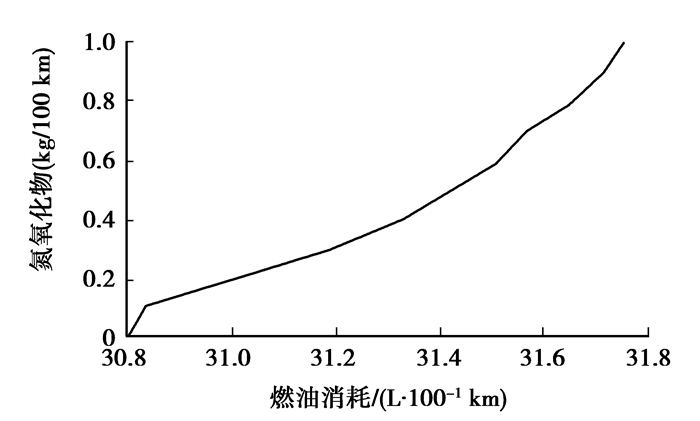
图 8是燃油消耗量随平衡因子变化的曲线。当平衡因子增加至1时,表示完全不在乎燃油消耗量,只追求最低的排放性能,因此造成了燃油消耗量激增,反之当平衡因子为0时,则表示只在乎燃油消耗,对排放性能不予关注,直接效果就是燃油消耗量明显降低。
|
图 8 平衡因子与燃油消耗量曲线 |
燃油经济性是通过测试车辆在底盘测功机上完成一个或多个行驶循环的燃油消耗量来评价的,由司机助显示屏幕给司机提供实际的和理论的行驶车速,帮助司机以规定的行驶循环驾驶车辆[18]。在进行规定循环工况试验时,驾驶员完全按照标准工况的期望车速行驶存在困难,允许存在一定的规定偏差。燃油实际消耗量由安装在车上油耗流量计获得,通过与实际燃油加注量进行比较,对该仪器进行了精度较正。
为了验证基于动态规划的换档决策的最优性和有效性,在北京试验场进行了8次中国典型城市公交循环工况下实车燃油经济性试验,试验结果及分析如下。
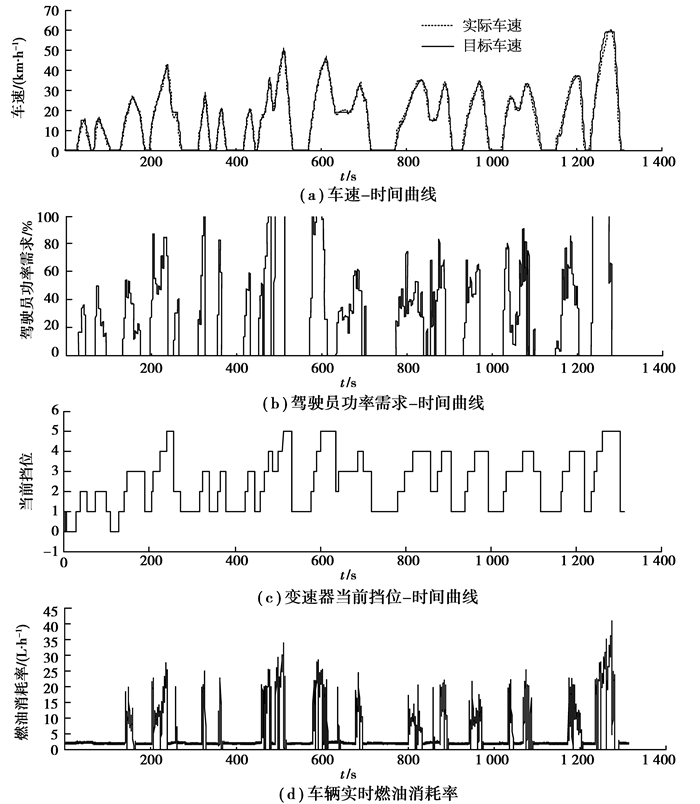
基于中国典型城市公交循环工况的实车道路燃油经济性试验曲线如图 9所示,图(a)为车速—时间曲线,与标准的中国典型城市公交循环工况相比,跟随性非常理想,速度偏差小于1 km/h;图(b)为驾驶员功率需求时间曲线;图(c)为变速器当前档位时间曲线,从图中可以看到没有出现循环换档现象,升档点的选择很好地体现了驾驶员意图;图(d)为车辆实时燃油消耗率,积分后换算至百公里燃油消耗量为28.55 L,得益于电能维持型整车能量管理策略,电池SOC终了值与试验开始前基本持平,整个循环工况过程换档决策合理有效。
|
图 9 基于中国典型城市公交工况的燃油经济性试验曲线 |
为了比较传统双参数和基于动态规划换档决策的实车燃油经济性,重复进行了8次中国典型城市公交循环工况下的试验,各次试验的百公里消耗量见表 3,两类换档决策的各次试验一致性较好,误差在合理范围内,其中基于动态规划换档决策的平均百公里燃油消耗量为28.037 L,较应用双参数换档决策的燃油经济性平均提高了近13.5%,换档总次数减少了15%,取得了较为明显的提升效果。
| 表 3 实车燃油经济性对比试验结果 |
笔者建立了某混合动力客车的整车仿真平台,提出了运用动态规划算法研究混合动力城市客车的换档决策问题,以目标泛函最小为目标,获得了中国典型城市公交工况下的最优换档决策序列,仿真和实车试验结果都显示了动态规划算法的优异性。该方法求解的结果可以用来评价其他类型换档决策,同时也可以通过分析动态规划算法的仿真结果,启发优化其他换档决策算法。
| [1] | 葛安林. 车辆自动变速理论与设计[M]. 北京: 机械工业出版社, 1991. |
| [2] | Pisu P, Rizzoni G. A comparative study of supervisory control strategies for hybrid electric vehicles[J]. Control Systems Technology, IEEE Transactions on, 2007, 15(3): 506–518. DOI:10.1109/TCST.2007.894649 |
| [3] | Lin C C, Peng H. Power management strategy for a parallel hybrid electric truck[J]. IEEE Transactions on Control Systems Technology, 2003, 11839. |
| [4] | Lin C C, Kang J M. Energy management strategy for parallel hybrid electric truck[J]. Proc. Amer. Control Conf, 2001: 2878–2883. |
| [5] | Sundstrom O, Soltic P, Guzzella L A. Transmission-actuated energy-management strategy[J]. Vehicular Technology, IEEE Transactions on, 2010, 59(1): 84–92. DOI:10.1109/TVT.2009.2030812 |
| [6] | CHO H S. Design of the powertrain system of a hybrid vehicle and development of its driving control algorithm[D]. Seoul:Seoul National University, 1998. |
| [7] | 古艳春. 混合动力汽车AMT换档策略及换档控制的研究[D]. 上海: 上海交通大学, 2006. |
| [8] |
王伟华, 王庆年, 曾小华.
并联混合动力汽车的换档规律[J]. 吉林大学学报:工学版, 2009, 39(1): 10–13.
WANG Weihua, Wang Qingnian, Zeng Xiaohua. Parallel hybrid electric vehicle shift algorithm[J]. Journal of Jilin University:Engineering and Technology Edition, 2009, 39(1): 10–13. (in Chinese) |
| [9] | 周国清. 混合动力大客车换档决策研究[D]. 上海: 上海交通大学, 2009. |
| [10] | 王康宁. 最优控制的数学理论[M]. 北京: 国防工业出版社, 1995. |
| [11] | Mansour C, Clodic D. Optimized energy management control for the Toyota Hybrid System using dynamic programming on a predicted route with short computation time[J]. International Journal of Automotive Technology, 2011, 13(22): 309–324. |
| [12] | Kutter S, B Ker B. Predictive online control for hybrids-resolving the conflict between global optimality, robustness and real-time capability[C]//Vehicle Power and Propulsion Conference (VPPC). New York:IEEE, 2010:1-7. |
| [13] | Vinot E, Trigui R, Jeanneret B, et al. HEVs Comparison and Components Sizing Using Dynamic Programming[C]//Vehicle Power and Propulsion Conference, New York:IEEE, 2007:314-321. |
| [14] | Wang R, Lukic S M. Dynamic programming technique in hybrid electric vehicle optimization[C]//Electric Vehicle Conference (IEVC). New York:IEEE, 2012:1-8. |
| [15] | Kolmanovsky I, Van Nieuwstadt M, Sun J.Optimization of complex powertrain systems for fuel economy and emissions[C]//Proceedings of the 1999 IEEE International Conference on, New York:IEEE, c1999:833-839. |
| [16] | Bertsekas D P, Dynamic programming and optimal control (3rd)[M]. Belmont, MA:Athena Scientific, 1995. |
| [17] | 重型混合动力电动汽车能量消耗量试验方法[S]. GBT 19754-2005. 北京: 国家标准化委员会, 2005. |
| [18] |
王志新, 吉学之, 支怀斌.
浅谈柴油机排放中的颗粒与烟度[J]. 柴油机, 2006(6): 19–21.
WANG Zhixing, JI Xuezhi, ZHI Huaibin. Particle and smoke in diesel engine's emission[J]. Diesel Engine, 2006(6): 19–21. (in Chinese) |
 2013, Vol. 36
2013, Vol. 36


