电阻抗成像技术(electrical impedance tomography,EIT)是近二十几年新兴的一种功能性医学成像技术。在人体皮肤表面放置电极,通过电极注入安全范围电激励,检测皮肤表面的电响应重构出人体内部电导率分布情况,与现今成熟的医学成像技术X射线计算机断层扫描(X-CT)、超声(Ultrasound)、核磁共振(MRI)等相比,EIT具有无创、廉价以及功能性成像等优势。但由于信息量有限、成像算法呈严重病态性等特点,使得EIT的分辨率受到限制[1-2]。
近几年EIT的研究通过增加电极的数量,获取更多的边界信息的方式,使二维成像转向三维成像,主要有:以色列T-SCANTM公司的TS 2000电阻抗扫描仪[3]、俄罗斯的MEIK®电阻抗乳腺诊断仪[4]、美国RPI的ACT-4[5-6]。由于EIT图像重建问题是一个非线性病态逆问题,其解存在严重的不适定性,至今没有一个令人满意的三维EIT图像重构以及显示算法。逆问题通常的解法是正则化方法,减小Jacobi矩阵的条件数,使解适定。而在三维问题中,由于计算场域的增加,将加剧病态性和计算复杂度[7]。
为解决三维EIT的图像重建问题,文中分析了Tikhonov正则化和一步牛顿法。这2种算法都能改变逆问题的性态,使之良态,在二维EIT中有比较好的效果,但在重构图像空间分辨率、消除伪迹、精度等方面存在不足[8]。将这2种算法组合的混合正则化算法,可进一步降低条件数,使重建过程趋于稳定,提高目标空间分辨率、成像深度。通过比较3种逆问题算法成像结果发现,混合正则化算法能提高图像质量,并且采用量化的重构质量评价判据,该算法的最大误差和平均误差更低。文中也给出目标在不同深度、不同位置的仿真结果,以香蕉和琼脂模型模拟生物体的物理实验结果,重构图像说明混合正则化算法可为三维EIT图像重建提供一种有效的方法。
1 三维EIT模型及混合算法 1.1 三维EIT模型及硬件系统EIT的激励方式分为电流激励和电压激励,辅助电极分为手电极和背电极,经过仿真研究,证明背电极电流激励模式的区分度高,即对被测场域内的电导率变化更加敏感[9]。研究采用这种方式,电极系统由8×8电极阵列和一个背电极组成。图 1(a)为测量系统及电极阵列的照片,电极直径4 mm,间距8 mm。图 1(b)为圆柱形三维EIT物理模型,圆柱上表面放置电极阵列,下表面放置背电极。电流由64个电极依次注入,背电极流出,测量另外63个电极对背电极的电压。一次测量可以得到64×63 =4 032次独立测量的数据,极大地增加了测量数据量。
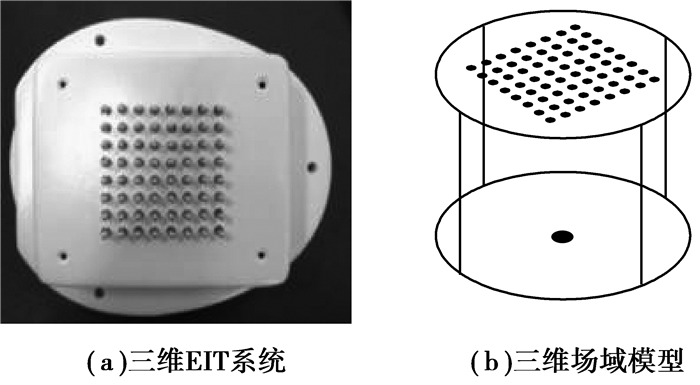
|
图 1 EIT系统组成及三维EIT模型 |
EIT正问题是已知场域内部电导率分布,计算边界电压;逆问题则是通过测量到的边界电压重构出测量场域的内部电导率分布,并显示重建图像。国内外学者已提出反投影法、正则化算法、D-Bar法和一步牛顿法等算法,但由于逆问题的病态性,至今还没有一个能精确计算逆问题的算法[10]。研究采用正则化思想来求解逆问题。假设均匀分布的场域中电导率为xp,施加电流激励后的边界电压为Vp。如果测量场域内电导率发生微小扰动,变化为δx,使此时场域内的电导率x≠xp,并且边界电压V≠Vp。可以得到
| $ \mathit{\boldsymbol{J}}\delta x = \delta V \Leftrightarrow \mathit{\boldsymbol{J}}\left( {{x_{\rm{p}}} - x} \right) = {V_{\rm{p}}} - V, $ | (1) |
式中J为雅克比矩阵。式(1)中只有电压V是测量得到的,均匀场域的边界电压Vp可以通过正问题计算得到
| $ \mathit{\boldsymbol{J}}\left( {{x_{\rm{p}}} - x} \right) = F\left( {{x_{\rm{p}}}} \right) - V, $ | (2) |
式中F(xp)表示场域中电导率为xp时的正问题仿真计算。式中只有扰动后的电导率分布x未知,一般采用最小二乘法求解,即
| $ \mathop {\min }\limits_{{x_{\rm{p}}} - x} {\left\| {\mathit{\boldsymbol{J}}\left( {{x_{\rm{p}}} - x} \right) - [F\left( {{x_{\rm{p}}}} \right)-V]} \right\|_2}。$ | (3) |
在这个线性最小二乘问题中,雅克比矩阵J是个病态矩阵。可以通过正则化使雅克比矩阵J变为良态矩阵,然后求解变化后的方程。最常用的正则化方法是Tikhonov正则化,该算法在目标函数中加入一个罚函数来实现对解的阻尼作用,达到使解稳定的目的,同时在一定程度上保证了解的空间分辨率。其一般形式为
| $ \begin{array}{l} \min \{ \left\| {\mathit{\boldsymbol{J}}\left( {{x_{\rm{p}}} - x} \right) - [F\left( {{x_{\rm{p}}}} \right)-V]} \right\|_2^2 + \\ \;\;\;\;\;\;\;\;\;\;\;\lambda \left\| {\mathit{\boldsymbol{L}}\left( {{x_{\rm{p}}} - x} \right)} \right\|_2^2\}, \end{array} $ | (4) |
式中:λ是Tikhonov正则化参数;L是正则化矩阵。文中λ取10-8,L选取为单位阵I。联立公式(2)~(4),得到EIT逆问题的Tikhonov正则化求解公式为
| $ \delta x = {x_{\rm{p}}} - x = {\left( {{\mathit{\boldsymbol{J}}^{\rm{T}}}\mathit{\boldsymbol{J + }}\lambda \mathit{\boldsymbol{I}}} \right)^{ - 1}}{\mathit{\boldsymbol{J}}^{\rm{T}}} \times [F\left( {{x_{\rm{p}}}} \right) - V]。$ | (5) |
Tikhonov正则化可以抑制EIT逆问题的解的震荡,使解稳定。虽然通过增加罚函数降低了雅克比矩阵的条件数,但是条件数仍然很大,并且通过仿真结果可知Tikhonov正则化在平滑重构图像的同时,降低了高阶信息的分辨率,成像结果存在伪迹,丧失了医学图像应有的对比度和锐度[11-12]。因此,有必要对Tikhonov正则化进行改造,以降低逆问题病态性,提高算法的分辨率。
一步牛顿法(NOSER)采用正则化的思想,JTJ的主对角元素(即diag(JTJ))作为罚函数为
| $ \delta x = {\left( {{\mathit{\boldsymbol{J}}^{\rm{T}}}\mathit{\boldsymbol{J}} + \varepsilon \times {\rm{diag}}\left( {{\mathit{\boldsymbol{J}}^{\rm{T}}}\mathit{\boldsymbol{J}}} \right)} \right)^{- 1}}{\mathit{\boldsymbol{J}}^{\rm{T}}} \times [F\left( {{x_{\rm{p}}}} \right)-V], $ | (6) |
式中ε是NOSER正则化参数,一般取值范围是0~1。NOSER算法在二维EIT中,成像效果较好,应用到平板电极结构的三维EIT时,可在小噪声干扰情况下正确重构出目标的大小、位置,随着噪声增加,图像质量下降。
由以上分析可知,如果将NOSER罚函数项添加到Tikhonov正则化中,可使得条件数进一步降低,减少图像伪迹,突出成像目标并增强抗噪声能力。混合正则化表达式为
| $ \delta x = {\left( {{\mathit{\boldsymbol{J}}^{\rm{T}}}\mathit{J + }\lambda \mathit{\boldsymbol{I}} + {\mathit{\boldsymbol{J}}^{\rm{T}}}\mathit{\boldsymbol{J}} + \varepsilon \times {\rm{diag}}\left( {{\mathit{\boldsymbol{J}}^{\rm{T}}}\mathit{\boldsymbol{J}}} \right)} \right)^{ - 1}}{\mathit{\boldsymbol{J}}^{\rm{T}}} \times\\\;\;\;\;\;\;\;[F\left( {{x_{\rm{p}}}} \right)-V]。$ | (7) |
对于不同的逆问题算法,通常的评估方式是直观的比较重构的图像,而不是定量地评估重构误差[13]。研究借鉴CT中对医学图像的评价方法,提出归一化均方距离判据和归一化平均绝对距离判据,为判断重构图像和原始图像的差异、计算重构误差提供一种客观标准[14]。
1.3.1 归一化均方距离判据(normalization mean square distance criterion,NMSD)归一化均方距离判据的表达式为
| $ {\rm{NMSD = [}}\frac{{\sum\nolimits_{i = 1}^N {{{\left( {{\sigma _{{\rm{true-}}\mathit{i}}}-{\sigma _{{\rm{rec-}}\mathit{i}}}} \right)}^2}} }}{{\sum\nolimits_{i = 1}^N {{{\left( {{\sigma _{{\rm{rec - }}\mathit{i}}} - \bar \sigma } \right)}^2}} }}{{\rm{]}}^{{\rm{1/2}}}}, $ | (8) |
式中σtrue-i和σrec-i是仿真模型图像和重构图像每个剖分单元的电导率,σ是仿真设定模型所有单元的平均电导率。当NMSD=0时,表示重构图像忠实再现设定的模型;NMSD的数值越大,表示两者差异越大,即重构误差越大。
1.3.2 归一化平均绝对距离判据(normalized mean absolute distance criterion,NMAD)归一化平均绝对距离判据表达式为
| $ {\rm{NMAD = }}\frac{{\sum\nolimits_{i = 1}^N {\left| {{\sigma _{{\rm{true - }}\mathit{i}}} - {\sigma _{{\rm{rec - }}\mathit{i}}}} \right|} }}{{\sum\nolimits_{i = 1}^N {\left| {{\sigma _{{\rm{true - }}\mathit{i}}}} \right|} }}。$ | (9) |
NMAD=0同样表示重构图像无误差。NMAD的数值越大,重构图像和设定的仿真模型图像偏差越大。
上述2个判据对不同类型的图像误差,其敏感程度是不同的。表面看来,NMSD和NMAD 2个参数意义相仿,且都有平均意义。仔细考察可知,NMSD较敏感地反映某几点产生较大误差的情况,而NMAD则较敏感地反映许多点均有一些小误差的情况。
2 仿真及物理实验结果 2.1 不同正则化算法比较为对比Tikhonov正则化和NOSER算法的重构结果,并说明混合正则化算法的优点,建立三维EIT系统的电磁场模型,如图 2(a)所示。圆柱高60 mm,半径55 mm,剖分为1 921个节点,9 036个四面体单元。成像目标是边长为15 mm的正方体,通过改变目标的深度比较几种正则化算法对不同深度目标的成像结果。图 2(a)中,目标上表面到圆柱上表面距离为10 mm。图 2(b)是模型的俯视图,目标放置在圆柱水平正中的位置。圆柱的电导率是1 S/m,目标的电导率是5 S/m。
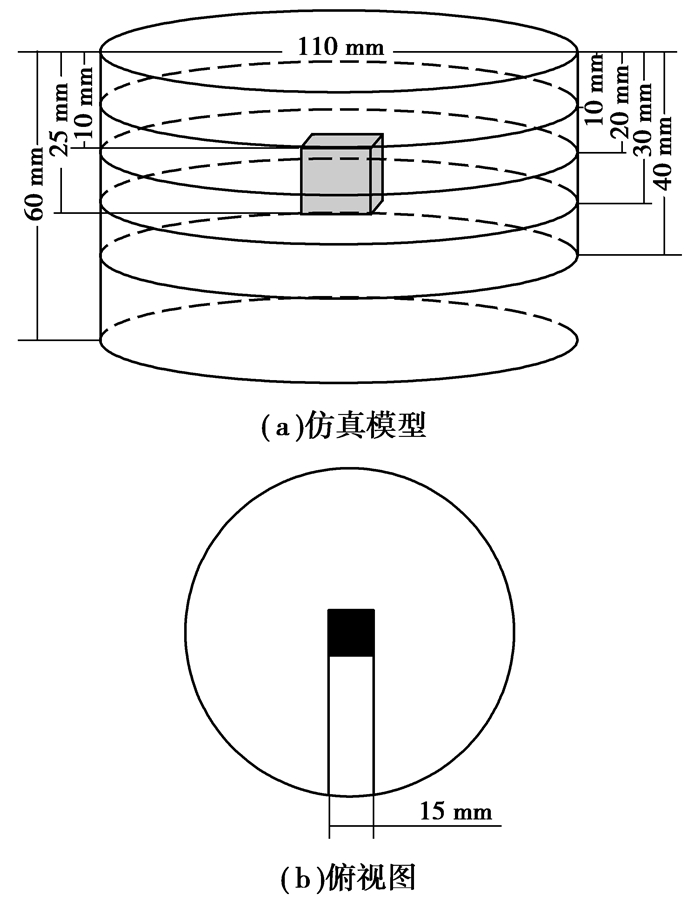
|
图 2 仿真模型(目标居中) |
EIT逆问题中的雅克比矩阵是病态矩阵,而矩阵如果是长方形矩阵或大型矩阵时,其病态性会加剧。以仿真模型为例,该模型的雅克比矩阵就是4 032×9 036的大型长方形矩阵,条件数达到1016。在三维EIT研究中,需要通过加密剖分提高成像精度,那样会使矩阵变得巨大,条件数同时增大。表 1中给出仿真模型雅克比矩阵及正则化后的条件数。从表中可看出,经过Tikhonov和NOSER正则化后,条件数都能降到1011以下,改善了逆问题的性态。而混合正则化则将条件数降至9.294×107,优于Tikhonov和NOSER正则化。
| 表 1 雅克比矩阵和经过正则化后的条件数 |
3种正则化算法的重构图像如图 3所示,分别显示深度1 cm、2 cm、3 cm、4 cm时的三维场域水平切面图像。分析图像结果,Tikhonov正则化可以正确定位目标,对比度高,但是重构出的目标体积变大,边界不明显。NOSER正则化重构图像的目标大小、位置正确,但目标与背景对比度不高,不如Tikhonov正则化重构的目标明显,在目标与背景电导率差异不大时,不易重构出目标图像。混合正则化算法能综合以上2种算法的优点,在目标图像变化不大的情况下,突出目标与背景的差异,提高重构的空间分辨率。表 2是3种算法的归一化平均绝对距离和归一化均方距离指标,从数值上看,混合正则化的误差至少比单独正则化算法误差降低50%,提高了重构算法的精度。

|
图 3 3种正则化算法的重构结果 |
| 表 2 3种正则化算法的重构误差 |
为研究混合正则化算法对不同位置成像目标的重构效果,移动目标在圆柱模型内的水平及垂直距离。所有的重构图像都是在仿真电压上加1%高斯噪声的结果。
2.2.1 目标在电极正下方图 4是目标在电极正下方的重构结果。图中目标1~3分别表示目标上表面至圆柱上表面距离为10 mm、20 mm、25 mm。目标在浅层时,目标空间位置、大小正确,图像分辨率高。当深度达到20 mm,即目标正方体在20~35 mm时,也可以成出目标位置,但略微变大,与背景的对比度不如浅层时明显。

|
图 4 不同深度的重构结果(目标居中) |
改变目标的水平位置,如图 5所示,成像目标在水平x、y方向上距离圆心20 mm。使得目标不在电极阵列的正下方,由于电极正下方的电流线分布最密,识别度也最高,这样可以研究混合正则化算法对电极阵列侧下方,电流线不密集区域的成像效果。
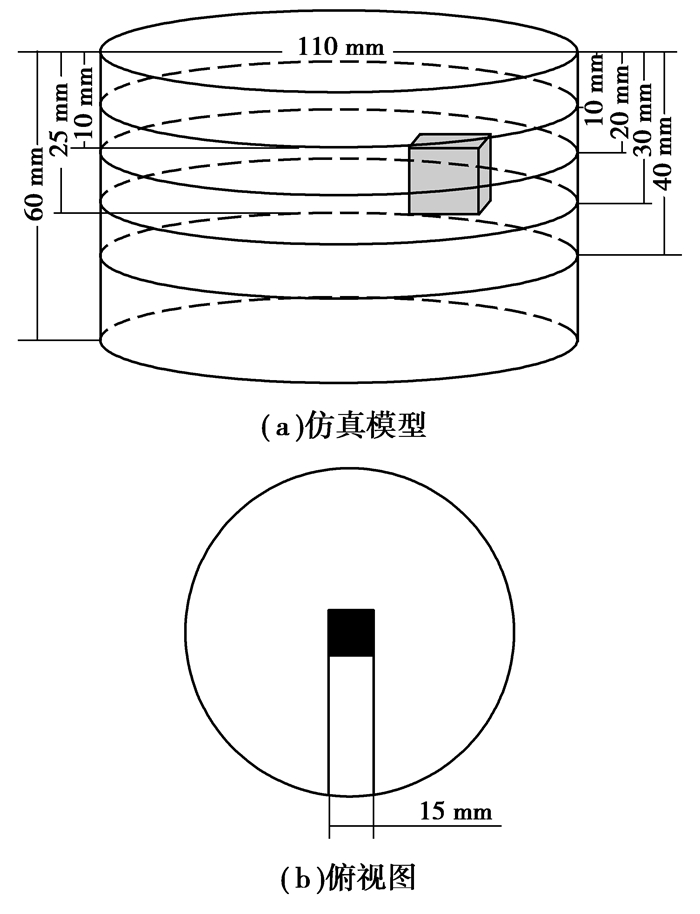
|
图 5 仿真模型(目标在电极侧下方) |
改变目标的深度,目标上表面至圆柱上表面距离分别为10 mm、20 mm、25 mm,图 6是重构结果的图像。和目标在在电极正下方结果相同,混合正则化算法能有效的重构出目标的位置及大小。只是当深度增加时,对目标大小重构有误差。如目标深度为25 mm时,深度2 cm的切面不应有目标图像,说明重构出的深层目标尺寸变大。

|
图 6 不同深度的重构结果(目标在电极侧下方) |
表 3量化比较了混合正则化算法对不同位置目标的重构结果。当目标的深度相同时,改变水平位置,重构的误差差异不大。目标深度增加也就是离电极阵列越远时,重构误差会变大。
| 表 3 目标在不同位置时的重构误差 |
综合以上仿真结果,不仅从直观的图像上,而且量化地从重构数据上比较,都证明混合正则化算法可以得到更好的空间分辨率,提高图像重构质量。
2.3 物理实验结果在仿真研究的基础上,利用三维EIT系统开展物理模型实验。实验模型如图 7所示,塑料盒长宽高分别为27 cm、20 cm和18 cm。首先在盒底部正中位置放置背电极,然后倒入加热的液态琼脂,待琼脂凝固后将一块15 mm × 9 mm × 9 mm的香蕉块埋在琼脂中,香蕉与背电极处于同一垂直位置。最后再浇入一层琼脂,使得香蕉的深度为2.5 cm,琼脂模型的总高度为6 cm。在实验中采用的激励电流为50 kHz,50 kHz时琼脂的电导率为8.8×10-2 S/m,香蕉为1.15×10-1 S/m[15]。实验时,将EIT测量探头放置在琼脂模型上,如图 7(b)所示。

|
图 7 物理实验模型及照片 |
因为琼脂是固态模型,目标在琼脂中不易移动,文中采用移动电极阵列位置的方式模拟改变目标水平位置。图 8给出两种相对位置的示意图,实验一将电极阵列放置在目标正上方,香蕉居于正中;实验二移动电极,香蕉在10号电极下方。
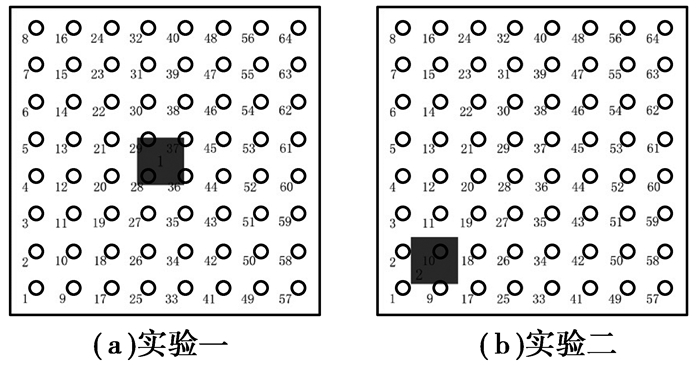
|
图 8 目标和电极阵列的相对位置(俯视图) |
实验结果如图 9所示。目标距离电极的距离是2.5 cm,从2 cm和3 cm切面图可以明显的识别出香蕉目标。改变水平位置后,即使香蕉不在电极正下方,也可以重构出图像。但是图中除香蕉目标外,其余区域颜色不一致,有很多斑点,造成造成图像不够平滑的原因有以下2点:1)为模拟人体测量的实际情况采用琼脂实验,电极阵列与琼脂表面的接触电阻大,不像水槽实验电极是浸入水中,可以良好接触,此时对测量系统的测量信噪比提出更高的要求;2)琼脂模型的制作需将琼脂粉放入水中加热至粘稠状,然后倒入塑料盒内凝固,在加热、搅拌和凝固时,琼脂可能溶解不均匀,使得琼脂并不是理想的电导率分布均匀的介质。

|
图 9 物理实验重构结果 |
从实验整体结果可说明三维EIT系统和混合正则化算法能够重构出目标的位置、大小和相对电导率,图像有较高的识别度和分辨率。
3 结论针对使用平板电极阵列的三维EIT系统图像重构算法精度不高、图像分辨率一般这些问题,对比研究Tikhonov和NOSER正则化算法,为改进算法在改变逆问题性态、消除伪迹、提高分辨率和图像对比度等方面存在的不足,提出综合Tikhonov和NOSER正则化的混合正则化算法。在评价逆问题重构效果上,提出归一化均方距离判据和归一化平均绝对距离判据,这2个判据可以量化的衡量算法的重构误差,为算法对比提供了新的手段。通过仿真实验,混合正则化算法在条件数上至少降低100倍,重构误差至少降低40%。从重构图像上看,目标空间分辨率、对比度都得到提高,改进了图像质量。在仿真基础上,应用三维EIT系统开展物理实验,结果表明混合正则化算法可以有效区分香蕉目标和琼脂。但是,物理实验重构的图像不平滑,存在斑点,需要进一步提高测量系统信噪比,优化混合正则化算法,这些问题将在后续工作中研究。
| [1] |
何传红, 何为, 黄嵩, 等.
开放式电阻抗成像基本原理和仿真实验研究[J]. 中国生物医学工程学报, 2008, 27(5): 669–674.
HE Chuanhong, HE Wei, HUANG Song, et al. Study on open electrical impedance tomography:basic theory, simulation and experiment[J]. Chinese Journal of Biomedical Engineering, 2008, 27(5): 669–674. (in Chinese) |
| [2] | ABASCAL J F, ARRIDQE S R, CAYFORD R H, et al. Comparison of methods for optimal choice of the regularization parameter for linear electrical impedance tomography of brain function[J]. Physiol Meas, 2008, 29(11): 1319–334. DOI:10.1088/0967-3334/29/11/007 |
| [3] | MICHEL A, ORAH L M, DOV M, et al. The T-SCANTM technology:electrical impedance as a diagnostic tool for breast cancer detection[J]. Physiological Measurement, 2001, 22(1): 1–8. DOI:10.1088/0967-3334/22/1/301 |
| [4] | VLADIMIR A C, ALEXANDER Y K, VLADIMIR N K, et al. Three-dimensional EIT imagine of breast tissues:system design and clinical testing[J]. IEEE Transactions on Medical Imaging, 2002, 21(6): 662–667. DOI:10.1109/TMI.2002.800602 |
| [5] | KAO T J, BOVERMAN G, KIM B S, et al. Regional admittivity spectra with tomosynthesis images for breast cancer detection:preliminary patient study[J]. IEEE Transactions on Medical Imaging, 2008, 27(12): 1762–1768. DOI:10.1109/TMI.2008.926049 |
| [6] | BOVERMAN G, KAO T J, ISAACSON D, et al. An implementation of calderon's method for 3D limited-view EIT[J]. IEEE Transactions on Medical Imaging, 2009, 28(7): 1073–1082. DOI:10.1109/TMI.2009.2012892 |
| [7] |
高鹤明, 许传龙, 王式民.
优化Tikhonov迭代法在电容层析成像中的应用[J]. 东南大学学报:自然科学版, 2010, 40(3): 527–532.
GAO Heming, XU Chuanlong, WANG Shimin. Application of optimized Tikhonov iterative algorithm for electrical capacitance tomography[J]. Journal of Southeast University:Natural Science Edition, 2010, 40(3): 527–532. (in Chinese) |
| [8] | GRAHAM B M, ADLER A. Electrode placement configurations for 3D EIT[J]. Physiological Measurement, 2007, 28(7): 29–44. DOI:10.1088/0967-3334/28/7/S03 |
| [9] |
李冰, 何为, 何传红, 等.
三维电阻抗成像系统激励模式仿真分析[J]. 重庆大学学报:自然科学版, 2012, 35(2): 78–86.
LI Bing, HE Wei, HE Chuanhong, et al. Simulation analysis on stimulation patterns of three-dimension electrical impedance tomography[J]. Journal of Chongqing University, 2012, 35(2): 78–86. (in Chinese) |
| [10] | STEPHENSON D R, MANN R, TORK T A. The sensitivity of reconstructed images and process engineering metrics to key choices in practical electrical impedance tomography[J]. Measurement Science and Technology, 2008, 19(9): 1–15. |
| [11] |
陈玉艳, 王旭, 吕轶, 等.
基于Tikhonov和变差正则化的磁感应断层成像重建算法[J]. 东北大学学报:自然科学版, 2011, 32(4): 460–463.
CHEN Yuyan, WANG Xu, Lü Yi, et al. An image reconstruction algorithm based on Tikhonov and variation regularization for magnetic induction tomography[J]. Journal of Northeastern University:Natural Science Edition, 2011, 32(4): 460–463. (in Chinese) |
| [12] |
黄嵩, 张占龙, 姚俊, 等.
基于混合正则化算法的颅内异物电阻抗成像仿真研究[J]. 中国生物工程学报, 2007, 26(5): 695–699.
HUANG Song, ZHANG Zhanlong, YAO Jun, et al. Electrical impedance tomography of intracranial foreign body based on mixed regularization algorithm[J]. Chinese Journal of Biomedical Engineering, 2007, 26(5): 695–699. (in Chinese) |
| [13] | WANG H B, XU G Z, ZHANG S A, et al. Implementation of generalized back projection algorithm in 3-D EIT[J]. IEEE Transactions on Magnetics, 2011, 47(5): 1466–1469. DOI:10.1109/TMAG.2010.2085423 |
| [14] | 庄天戈. CT原理与算法[M]. 上海: 上海交通大学出版社, 1992. |
| [15] | SEO J K, LEE J, KIM S W, et al. Frequency-difference electrical impedance tomography (fdEIT):algorithm development and feasibility study[J]. Physiological Measurement, 2008, 29(8): 929–944. DOI:10.1088/0967-3334/29/8/006 |
 2013, Vol. 36
2013, Vol. 36


