可变信息标志(variable message signs,VMS)是用来向用路者提供道路交通状况、气象状况及其他道路交通相关信息的一种外部设备。从1970年代中后期,美国学者就对VMS进行了多方面的研究[1-4],在研究应用的基础上,陆续发布了一系列的指南和手册[5-9]。在对VMS的诸多研究中,选址问题起步较晚。其中,Jeffrey M. Henderson[10]建立了VMS选址优化模型,使用遗传选择模型确定可变交通标志的最佳布置位置;Abbas等[11]提出了对路网上的VMS进行选址优化,以最大程度地减少车辆延误为优化目标,采用确定型排队模型估计有无VMS情况下的车辆延误情况;Yi Chang Chiu等[12]利用双层随机整数规划模型来描述可变信息标志的选址问题;梅振宇等[13]、Yang等[14]、尚华艳等[15]分别采用遗传算法、OD估算、元胞传输模型对VMS选址问题进行研究。在对VMS的研究应用中逐渐意识到:VMS选址得当不仅可以改善路段交通状况,而且会提高到整个路网的通行效率。而上述研究成果,并未准确地回答这个问题。
在某一特定的区域内,在若干路段上设置VMS,VMS可以向驾驶员提供前方道路的路况信息。对于城市中某些出行驾驶群体,会有一些驾驶员在接受了所发布的交通信息后,其路径选择行为会发生变化,如图 1所示。这些驾驶员路径选择的变化会导致路网交通流发生重新分配,进而路网的运行状态也会发生一定的改变。如果通过合理的设置VMS达到合理引导交通流分配的作用,那么区域内全体出行者的总出行成本会相应的降低,从而达到全局层面的优化效果。
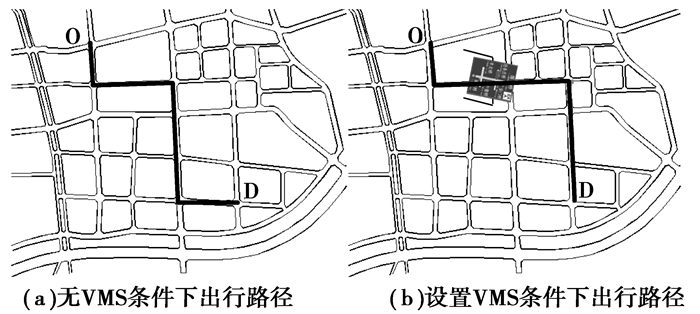
|
图 1 可变信息标志作用原理 |
研究结果表明:VMS可以使驾驶员对路段的感知行程时间更加接近路段的实际行程时间,即降低驾驶员对路段感知行程时间的误差[16],而这种误差会影响驾驶员的选择行为。在路网中不同位置的VMS会影响驾驶员感知行程时间,进而影响路网流量的分布,即交通分配的结果。不同的流量会影响到路段和交叉口的行程时间,从而会影响到整个路网的运行情况。在上述认知的基础上,文章以路网总期望出行时间描述路网运行情况,以路网总期望出行时间最短为目标,提出了VMS选址分析流程,并进行了算例验证该流程。
1 VMS宏观选址研究思路VMS是一种交通信息发布手段,通过它可实现路网流量均衡分配。在路网某一位置设置VMS时,由于VMS的流量再分配作用,VMS所指示的路段上车辆到达率与未设置VMS相比,会发生一定的变化,如图 2所示。图 2中阴影部分为是否发布道路信息情况下延误的变化情况,也可以看作是VMS所指示的路段的收益。
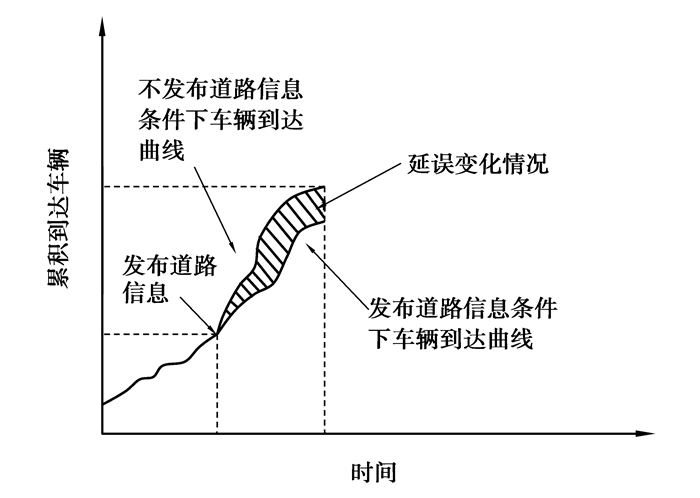
|
图 2 有无道路信息条件下路网运行情况 |
设置VMS情况下,驾驶员得到了相应路段的路况信息,驾驶员对路段的感知行程时间会在一定程度上接近路段的实际行程时间,也就是说驾驶员对路段感知行程时间的误差会降低。文章假设该误差服从随机正态分布,以Probit模型为基础建立提供道路信息条件下的交通流分配方法,分析在不同路段设置VMS后的分配结果。通过比较不同路段设置VMS的路网总期望出行时间,得到VMS的最优选址位置。
2 提供道路信息条件下交通流分配研究以随机分配模型为基础,描述提供道路信息条件下路网流量的分配结果。
随机分配是针对单一路径分配的不足而提出来的,即研究用户有不同感知阻抗的情形下的多路径分配。因此,关于随机分配在有的文献中也叫做“多路径分配”,或者“随机加载分配”。
研究以Probit模型为基础讨论道路交通信息对交通流量分配的影响。假设出发地为r,目的地为s的OD间的第k条路径上的道路感知行程时间可以表示为
| $ C_k^{rs} = c_k^{rs} + \varepsilon _k^{rs}, \forall r, s, k, $ | (1) |
式中:Ckrs为道路感知行程时间;ckrs为道路实际行程时间;εkrs为随机误差项,随机误差项满足E(εkrs)=0。
将第k条路径上的道路感知行程时间表示成各路段感知行程时间和的形式为
| $ C_k^{rs} = \sum\limits_a {{C_{a, k}}^{rs}\delta _{a, k}^{^{rs}}}, \forall r, s, k, \mathit{a} \in {\mathit{L}_\mathit{k}}, k \in \kappa, $ | (2) |
式中,
对于每一条路段有
| $ C_{a, k}^{rs} = c_{a, k}^{rs} + \varepsilon _{a, k}^{rs}, \forall r, s, k, \mathit{a} \in {\mathit{L}_\mathit{k}}, k \in \kappa, $ | (3) |
式中:Ca,krs为路段a的感知行程时间;ca,krs为路段a的实际行程时间;εa,krs为随机误差项,随机误差项满足E(εa,krs)=0,
| $ \begin{array}{l} \mathit{E}\left( {\varepsilon _{a, k}^{rs}} \right) = 0, \\ C_k^{rs} = \sum\limits_a {\left( {c_{a, k}^{rs} + \varepsilon _{a, k}^{rs}} \right) \cdot \delta _{a, k}^{^{rs}}}, \forall r, s, k, \mathit{a} \in {\mathit{L}_\mathit{k}}, k \in \kappa 。\end{array} $ | (4) |
随机误差项εa,krs~N(0,θca,krs),θ是表征道路信息水平的变量。当某一路段在不提示道路信息的情况下,道路使用者对路段的感知行程时间与路段的实际行程时间偏差较大,θ也就越大;当某一路段提示道路信息时,道路使用者对路段的感知行程时间将会接近路段的实际行程时间,θ也就越小。当所提供的道路信息越准确的时候,道路使用者对路段的感知行程时间将会越接近路段的实际行程时间,θ也就越小。不同的θ值代表不同的道路信息水平,因此,在分配交通流量的过程中,不同的道路信息提示情况将会产生不同的交通流量分配结果。
3 VMS选址计算流程VMS选址计算流程如图 3所示。
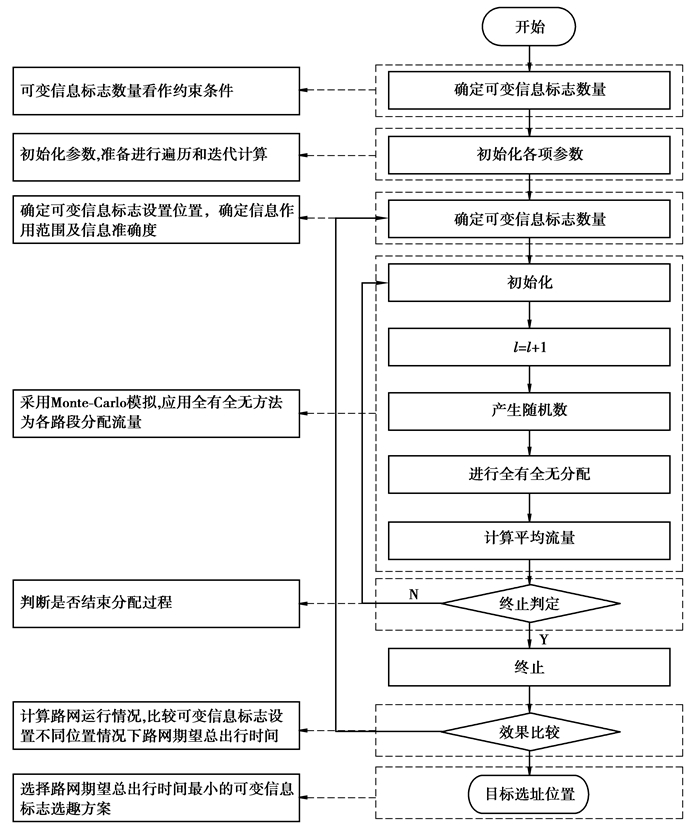
|
图 3 VMS选址计算流程图 |
Probit模型建立在随机项的联合密度函数为多元正态分布的基础上,因为多元正态分布函数不能直接积分求出,因此某一项被选择的概率不能由解析式表示。解决该问题通用的做法是采用Clark循环逼近法或者Monte Carlo模拟法来解决。文中采用Monte Carlo模拟法求解Probit模型分配问题。
在应用全有全无分配为各路段分配流量的过程中,用xa(l)记录第l次迭代时路段a的分配到的流量值。历次迭代的流量可以根据xa(l)=[(l-1)xa(l-1)+Xa(l)]/l得到。
在判定时候结束分配的过程中,δa(l)表示路段a在第l次迭代时的标准差,则
研究选择一棋盘状路网进行计算对VMS选址方法进行解释说明。算例路网中共有16个节点,表示16个交叉口,节点之间共有24条连接线,表示24条路段。交叉口采用信号控制。路网情况如图 4所示。
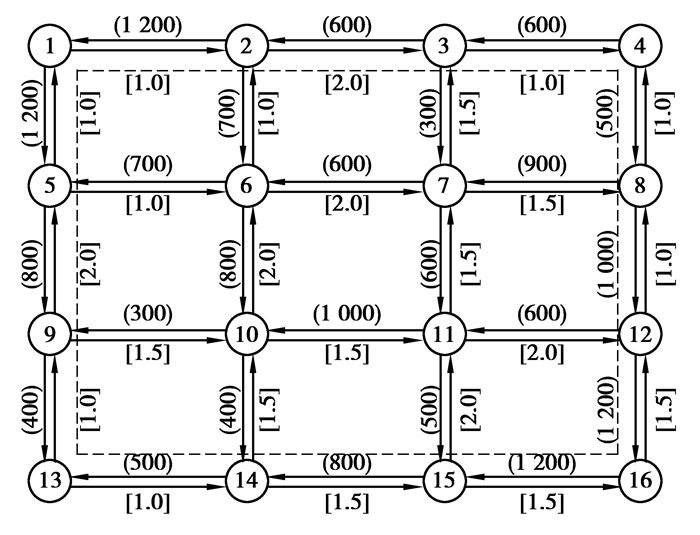
|
图 4 算例路网示意图 |
算例选择在上图路网中心路段上设置VMS。上图中红色区域涵盖的各路段为设置VMS的备选路段,VMS指示前方临近3条道路的交通信息。无VMS情况下道路信息水平θ为0.5,设置VMS情况下道路信息水平θ′为0.1。
4.2 路网要素基本属性路网中路段属性标注于图 4中,其中括号()表示路段通行能力,单位为veh/h,括号[]表示路段自由流行程时间,单位为min。交叉口信号周期120 s,绿灯时长60 s,分析持续时间1 h,增量延误系数为1,限流系数为1。
4.3 路网运行情况表征研究采用路网总期望出行时间表征路网运行情况。路网总期望出行时间包括路网中路段和交叉口的期望行程时间。对于路段而言,期望出行时间采用BPR函数进行计算。对于交叉口而言,将其抽象成无距离的节点,其期望出行时间与其延误相等,采用HCM 2000模型计算交叉口计算交叉口延误。由于篇幅限制,BPR函数和HCM 2000延误计算模型不一一列举。
4.4 交通流分配终止迭代常数的确定图 5中括号中数字表示路段名称,横轴为迭代次数,纵轴为路段流量。可以发现,在k>0.1时路段流量波动依然很显著,在k < 0.1时各路段流量才比较平稳。由于篇幅限制,只列出4条路段的流量波动情况,其他路段情况类似。
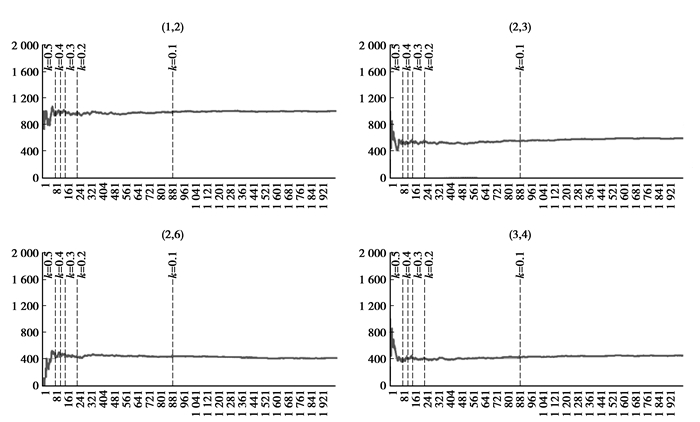
|
图 5 不同判定标准情况下路网部分路段流量波动情况 |
算例路网设置一个VMS时,不同位置条件下路网总期望出行时间各不相同,大约为1 495~1 611 s,显示出一定的波动性。通过比较不同位置路网总期望出行时间,如图 6所示。
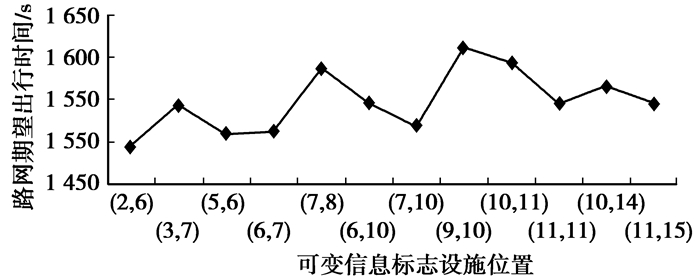
|
图 6 设置一个VMS情况下路网运行情况 |
位置1设置VMS路网总期望出行时间最小,达到1 495.9 s,认为路段(2,6)设置VMS最优。图中虚线为不设置VMS时路网运行状态(1 524.9 s)。
算例路网设置2个VMS时,不同位置条件下路网总期望出行时间大约为1 457~1 695 s,也显示出了一定的波动性。通过比较不同位置路网总期望出行时间,如图 7所示,路段组合(2,6)-(6,7)设置VMS路网总期望出行时间最小,为1 457.6 s,认为路段组合(2,6)-(6,7)设置VMS最优。图中虚线为不设置VMS时路网运行状态(1 524.9 s)。
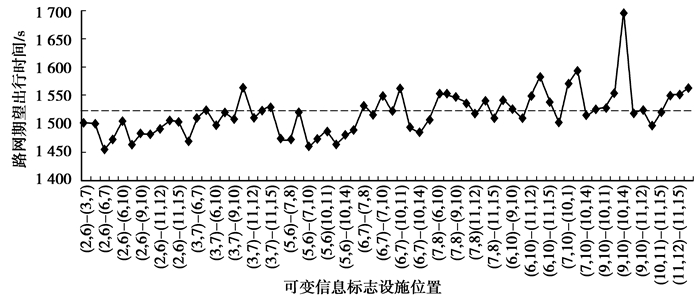
|
图 7 设置2个VMS情况下路网运行情况 |
对可变信息标志选址相关的2个问题进行讨论,主要讨论信息覆盖范围对路网运行情况的影响以及信息准确度对路网运行情况的影响。
5.1 信息覆盖范围对路网运行情况的影响为了讨论信息覆盖范围对路网运行情况的影响,文中依然采用选址算例中的路网。为不同路段提供交通信息,考察不同信息覆盖范围条件下路网的总期望出行时间的变化情况。表 1为提示信息路段情况表,表中情况O到情况L表示不断地增加提示信息路段的数量,也就意味着提高了信息覆盖范围。
| 表 1 提示信息路段情况表 |
通过计算不同信息覆盖范围情况下路网的总期望出行时间(见图 8),图中虚线为不设置VMS时路网运行状态(1 524.9 s)。发现在整体趋势上随着信息覆盖范围的扩大,路网总期望出行时间有减小的趋势。结果表明:正确设置VMS可以在一定程度上改善路网运行状态,可以作为交通需求管理的手段,从而收到有益的效果。除此之外,应尽可能地采取各类措施,比如设置VMS、发布交通信息广播等,有效降低路网的总期望出行时间,从而达到提高路网运行效率的目的。
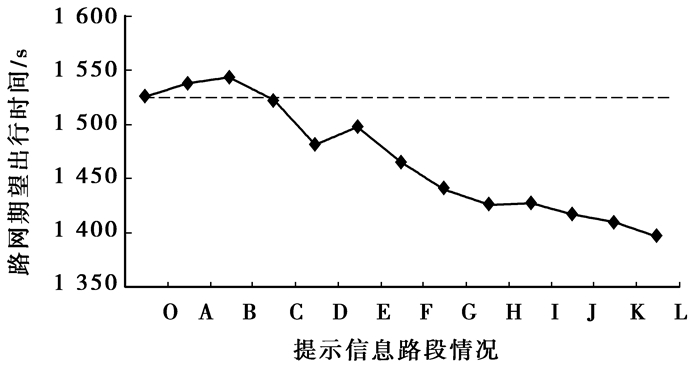
|
图 8 不同信息覆盖范围路网的运行情况 |
但同时需要指出的是,图 6~图 8中路网运行状态都表现出了一定的波动性,在一定的情况下设置VMS后路网运行状态不一定得到改善,其路网期望出行时间可能高于不设置VMS时的路网期望出行时间。结果说明:在设置VMS时要采取审慎的态度,不恰当的选址方案可能并不能带来有益的结果。
5.2 信息准确度对路网运行情况的影响出行者对道路行程时间的随机误差项εa,krs~N(0,θca,krs),其中θ是表征道路信息水平的变量。当所提供的道路信息越准确的时候,道路使用者对路段的感知行程时间将会越接近路段的实际行程时间,θ也就越小;反之亦然。可变信息标志所发布的信息类型有很多,比如预测信息、实时信息、历史信息等,这些都影响当前对路网的认识。除此之外,发布的信息类型也对认识当前路网有着影响,比如地图式的可变信息标志和文字式的可变信息标志带给人们的认识就会有所不同。
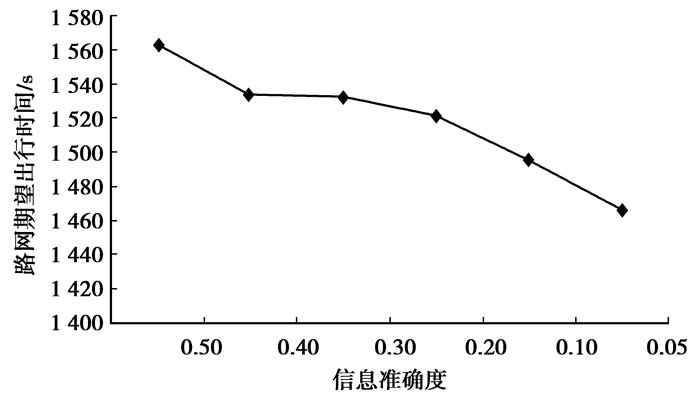
文章采用选址算例中的路网,讨论不同信息准确度情况下路网的运行情况。图 9为在路段(2-6)设置可变信息标志时,θ选取0.5、0.4、0.3、0.2、0.1、0.05共6个水平条件下路网总期望出行时间的变化情况。
|
图 9 不同信息准确度条件下路网的运行情况 |
通过计算信息准确度条件下路网的总期望出行时间(见图 9),发现在整体趋势上随着信息覆准确度的提高,路网总期望出行时间有减小的趋势。结果表明:交通管理者应该尽可能提高信息的发布精度,使出行者更加准确地掌握道路的实际状况,从而提高路网运行效率。
6 结论研究主要讨论VMS的宏观选址问题,即在路网范围内,确定VMS所设置的路段。所提出的VMS选址方法,是在Probit分配模型的基础上,通过对随机误差项的讨论,确定提供道路信息条件下交通流分配情况。不同的分配情况,会带来不同的路网运行结果。采用BPR函数和HCM 2000的交叉口延误计算方法评价路网的运行情况,明确VMS选址计算流程。以上述方法为基础,以4×4节点的棋盘状路网作为算例路网,进行VMS选址的算例计算。
在算例中,分别计算并得到了设置1个和2个VMS时的最优选址方案。此外,文章还讨论了信息覆盖范围对路网运行情况的影响以及信息准确度对路网运行情况的影响。结果表明,随着信息覆盖范围的扩大以及信息准确度的提高,路网总期望出行时间有减小的趋势。算例中路网不同位置设置VMS时路网运行情况呈现一定的波动。结果说明:在设置VMS时要采取审慎的态度,不恰当的选址方案可能并不能带来有益的结果。
| [1] | DUDEK C L, MAST T M, RICHARDS S H, et al. Human factors requirements for real-time motorist information displays. Volume 1:design guide. Final report[M]. Washington D C:Federal Highway Administration, 1978. |
| [2] | DUDEK C L. Human factors requirements for real-time motorist information displays. Volume 2:state-of-the-art:messages and displays in freeway corridors. Final report[R]. Springfield Va:National Technical Information Service, 1978. |
| [3] | TURNER J M, DUDEK C L, CARVELL J D. Real-time diversion of freeway traffic during maintenance operations[J]. Transportation Research Record, 1978(683): 8–10. |
| [4] | DUDEK C L, HUCHINGSON R D. Manual on real-time motorist information displays[M]. Springfield Va.: National Technical Information Service, 1986. |
| [5] | DUDEK C L. Guidelines on the use of changeable message signs[C/OL]. Washington D C:Department of Transportation, 1991.http://ntl.bts.gov/lib/jpodocs/repts_te/3726.pdf. |
| [6] | MCCOY P T, PESTI G. Incident management:changeable message sign deployment guidelines, PB2001-101823[R]. Nebraska:University of Nebraska, 1999. |
| [7] | DUDEK C L, TROUT N, DURKOP B, et al. Improving dynamic message sign operations[R]. Texas:Texas Transportation Institute, 2000. |
| [8] | JUHA L, PIRKKO R, KATHARINE M. Understanding control strategies and technical features of VM signs[J]. Traffic Engineering & Control, 2001, 42(5): 168–171. |
| [9] | DUDEK C L. Variable message sign operations manual[C/OL]. Trenton:New Jersey Department of Transportation, FHWA-NJ-2001-10, 2001.http://ntl.bts.gov/lib/24800/24856/VMS_Manual.pdf. |
| [10] | JEFFREY H. A Planning model for optimizing locations of changeable message signs[D]. Ontario:University of Waterloo, 2004. |
| [11] | ABBAS M M. Optimizing variable message sign locations on freeways using genetic algorithms[M]. Nebraska: University of Nebraska-Lincoln, 1997. |
| [12] | CHIU Y C, NHAN H, MAHMASSANI H S. Determining optimal locations for variable message signs under stochastic incident scenarios[C]//Proceedings of the 80th Transportation Research Board Annual Meeting, January 1-11, 2001, Washington, D C, U S.[2013-01-12].http://trid.trb.org/view.aspx?id=675731. |
| [13] |
梅振宇, 项贻强, 陈峻, 等.
城市交通流诱导信息板配置优化方法[J]. 交通运输工程学报, 2007, 7(5): 88–92.
MEI Zhenyu, XIANG Yiqiang, CHEN Jun, et al. Optimization method of configuration of traffic flow guidance information board in urban[J]. Journal of Traffic and Transportation Engineering, 2007, 7(5): 88–92. (in Chinese) |
| [14] | YANG H, ZHOU J. Optimal traffic counting locations for origin destination matrix estimation[J]. Transportation Research Part B:Methodological, 1998, 32(2): 109–126. DOI:10.1016/S0191-2615(97)00016-7 |
| [15] |
尚华艳, 黄海军, 高自友.
基于元胞传输模型的可变信息标志选址问题研究[J]. 物理学报, 2007, 56(8): 4342–4347.
SHANG Huayan, HUANG Haijun, GAO Ziyou. Locating the variable message signs by cell transmission model[J]. Acta Physica Sinica, 2007, 56(8): 4342–4347. DOI:10.7498/aps.56.4342 (in Chinese) |
| [16] | LAM W H K, CHAN K S. A stochastic traffic assignment model for road network with travel time information via variable message signs[C]//Proceedings of the 1996 Intelligent Vehicles Symposium, September 19-20, 1996.Tokyo, Japan. Piscataway:IEEE Press, 1996:99-104. |
 2013, Vol. 36
2013, Vol. 36

