基于感应耦合电能传输技术的非接触电能传输(inductive power transfer,IPT)系统解决了传统供电方式在特殊场合(水下或易燃易爆等场合)和移动设备供电等情况下存在的问题和缺陷[1-4]。IPT系统由负责完成能量变换与传送的原边电路和负责能量拾取与变换的副边电路两部分组成。系统通过电磁感应与耦合原理实现电能从原边电路到副边电路的传递。
在IPT系统中,原边电路往往采取基于谐振工作模式的高频电力电子能量变换电路,这种方式不但可以为逆变机构提供软开关条件,而且可以增大原边发射线圈中的电流,从而降低开关损耗,提高系统的传输功率和传输效率。副边拾取电路通过与原边线圈耦合拾取能量,负载通过拾取电路获取能量,并最终以反射阻抗的形式影响原边电路。在实际应用中,负载的随机性会引起系统谐振频率的变化。然而,研究发现,谐振频率发生变化后,如不调节开关频率与谐振频率一致,会破坏逆变机构的软开关状态,导致开关管在非零点切换,从而形成环流。环流会导致EMI增强,开关管损耗增大,影响系统的传输效率和稳定性[5-6]。
笔者以负载并联谐振型全桥逆变器为例分别分析了开关管在谐振电压过零点之前和过零点之后切换时环流的特点以及开关频率与谐振频率之间的关系,提出一种通过实时检测环流方向,动态调节开关频率与谐振频率一致,实现ZVS(zero voltage switching),从而抑制环流的方法,实验结果验证了该方法的有效性。
1 环流产生机理分析推挽式逆变器和全桥逆变器是目前应用较广泛的两种负载并联谐振型逆变器结构。由于这两种拓扑结构都有环流问题存在且工作过程类似,以负载并联谐振型全桥逆变器为例,分别分析开关管在谐振电压过零点之前和过零点之后切换时环流的特点。
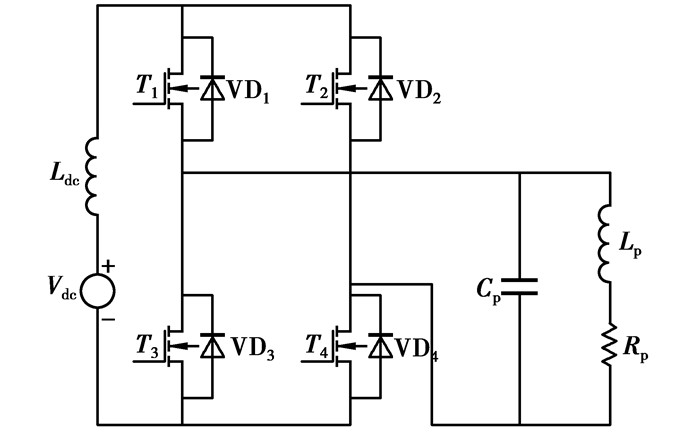
如图 1所示,电压源Vdc和电感Ldc串联得到等效电流源。逆变电路共有2个桥臂,T1和T4为一开关对,T2和T3为一开关对。电容CP与电感LP及其内阻RP组成并联谐振网络。通过控制开关管对交替导通180°,就可以将直流电流源变换成高频交流电流源。
|
图 1 负载并联谐振型全桥逆变电路 |
副边拾取电路与原边电路只有相互耦合关系,其对原边电路的影响只表现为电感LP和电阻RP的变化。首先分析空载时原边回路的电路情况。由图 1可推出并联谐振网络基波总等效阻抗为
| $ \begin{gathered} Z = \frac{{{R_{\rm{p}}}}}{{{{\left( {1-{\omega ^2}{L_{\rm{p}}}{C_{\rm{p}}}} \right)}^2} + {\omega ^2}R_{\rm{p}}^2C_{\rm{p}}^2}} + \hfill \\ i\frac{{\omega \left( {{L_{\rm{P}}}-R_{\rm{p}}^2{C_{\rm{P}}}-{\omega ^2}L_{\rm{p}}^2{C_{\rm{p}}}} \right)}}{{{{\left( {1 - {\omega ^2}{L_{\rm{p}}}{C_{\rm{p}}}} \right)}^2} + {\omega ^2}R_{\rm{p}}^2C_{\rm{p}}^2}}, \hfill \\ \end{gathered} $ | (1) |
式中ω=2πf0(f0为谐振网络的固有谐振频率),则
| $ {f_0} = \frac{{\sqrt {{C_{\rm{p}}}\left( {{L_{\rm{p}}} - R_{\rm{p}}^2{C_{\rm{p}}}} \right)} }}{{2\pi {L_{\rm{P}}}{C_{\rm{P}}}}}, $ | (2) |
从式(2)可以发现,拾取电路对LP或RP的影响必然会导致谐振频率的变化。
为了适应不同的用电设备,IPT系统的副边电路可以采用并联谐振或串联谐振两种方式[7-13]。不失一般性,假设系统中谐振回路皆工作于完全谐振状态。以下分别分析副边拾取电路采取不同谐振方式时系统工作频率的变化情况。
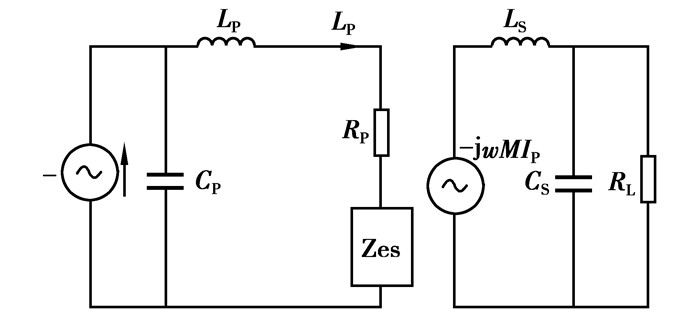
副边拾取采用并联谐振方式时系统的等效电路如图 2所示。
|
图 2 副边为并联谐振拓扑的系统等效电路 |
图中I是来自逆变桥的等效交流方波电流源,CP为原边电路谐振电容,LP为原边电路谐振电感,Zes为拾取反射阻抗,RP为电缆自身电阻,jωMIp是原边导轨电流在副边拾取线圈中产生的互感电动势,CS为副边电路谐振电容,LS为负载拾取线圈电感,RL为用电设备等效电阻。拾取电路输入阻抗为
| $ {Z_{\rm{S}}} = \frac{{{L_{\rm{S}}}{R_{\rm{L}}}}}{{{L_{\rm{S}}} + R_{\rm{L}}^2{C_{\rm{S}}}}} + i\frac{{{L_{\rm{S}}}\sqrt {{L_{\rm{S}}}{C_{\rm{S}}}} }}{{\left( {{L_{\rm{S}}} + R_{\rm{L}}^2{C_{\rm{S}}}} \right){C_{\rm{S}}}}}, $ | (3) |
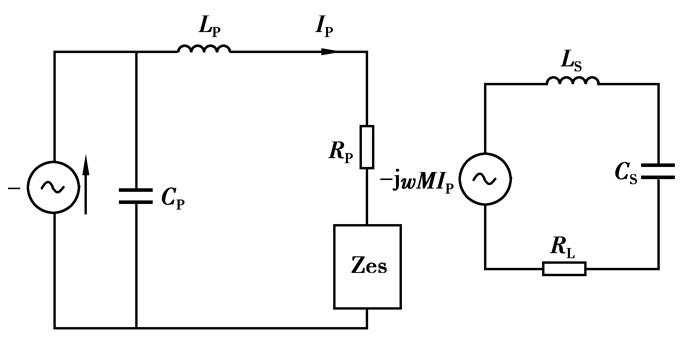
副边拾取采用串联谐振拓扑时系统等效电路如图 3所示。
|
图 3 副边为串联谐振拓扑时系统等效电路图 |
谐振时其等效阻抗为
| $ {Z_{\rm{S}}} = {R_{\rm{L}}}。$ | (4) |
反射阻抗为
| $ Z{\rm{es = }}\frac{{{\omega ^2}{M^2}}}{{{Z_{\rm{S}}}}}。$ | (5) |
由式(2)、(3)、(4)、(5)可以明显看出,副边拾取采用并联谐振,负载反射到原边的等效阻抗成容性和阻性,拾取采用串联谐振,反射阻抗成阻性。因此无论副边电路采用哪种谐振方式,一旦用电设备发生变化,则原边谐振频率就会产生变化[14-16]。
下面详细分析谐振频率变化对系统的影响以及系统中环流特点。
负载谐振型逆变器通过开关管的切换来提高电流频率,系统的工作频率是由开关频率f决定的。当谐振频率发生变化时,若调节开关频率跟随谐振频率变化,则开关管可以在谐振电压Vc过零点切换,不会形成环流。
当谐振频率小于开关频率时,即f >f0时,开关管在谐振电容电压Vc过零点之前开通或关断。此时谐振电容和电源会被新开通的开关管及另一桥臂开关管的反并联二极管短路,这会引起很高的瞬时短路电流,在开关管中形成环流。如图 4所示。
|
图 4 f>f0时开关管在谐振电压过零点之前切换 |
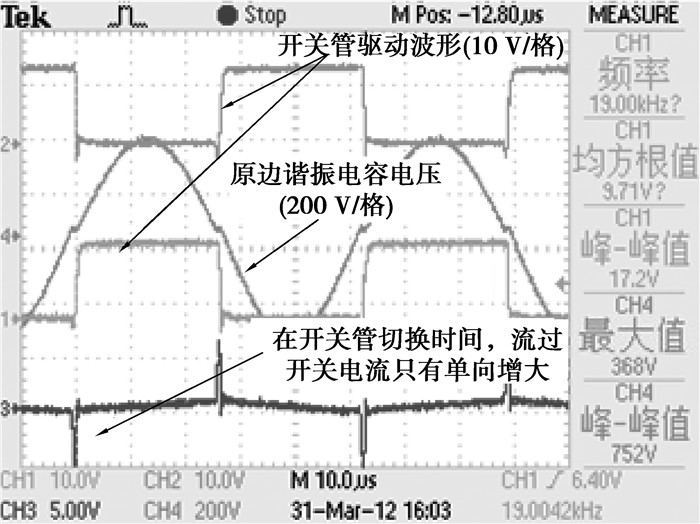
当谐振频率大于开关频率时,即f < f0时,开关管在谐振电容电压Vc过零点之后开通或关断。此时,谐振电容同样会被短路,而且在这种情况下,短路回路中将有很大的谐振电流流过且稍后会被开关管强制关断,这样会造成开关管的di/dt过大,造成较大的开关损耗,甚至损坏开关管。这时开关管中会产生很大的尖峰电流。如图 5所示。
|
图 5 f < f0时开关管在谐振电压过零点之后切换 |
另外,从图 4和图 5可以发现,当开关频率大于谐振频率时,流过开关管的尖峰电流具有双向性,而反之则不存在。这是由于开关频率大于谐振频率时,开关管在谐振电压过零点前切换,此时开关管在开关管的能量和谐振电容的能量均没有释放完的情况下就进行了换向动作的结果。
2 环流抑制方法由上面的分析可知,开关管在谐振电容电压过零点切换的时候,会形成环流。因此调节开关频率与谐振频率一致,使开关管在谐振电压过零点切换,即实现ZVS软开关,是抑制环流的关键。
要调节开关频率与谐振频率一致,首先要确定开关频率的补偿方向,其次要确定补偿方式。
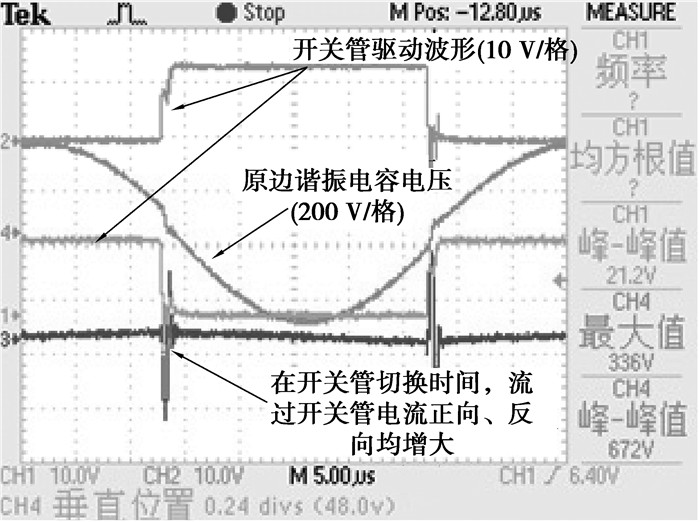
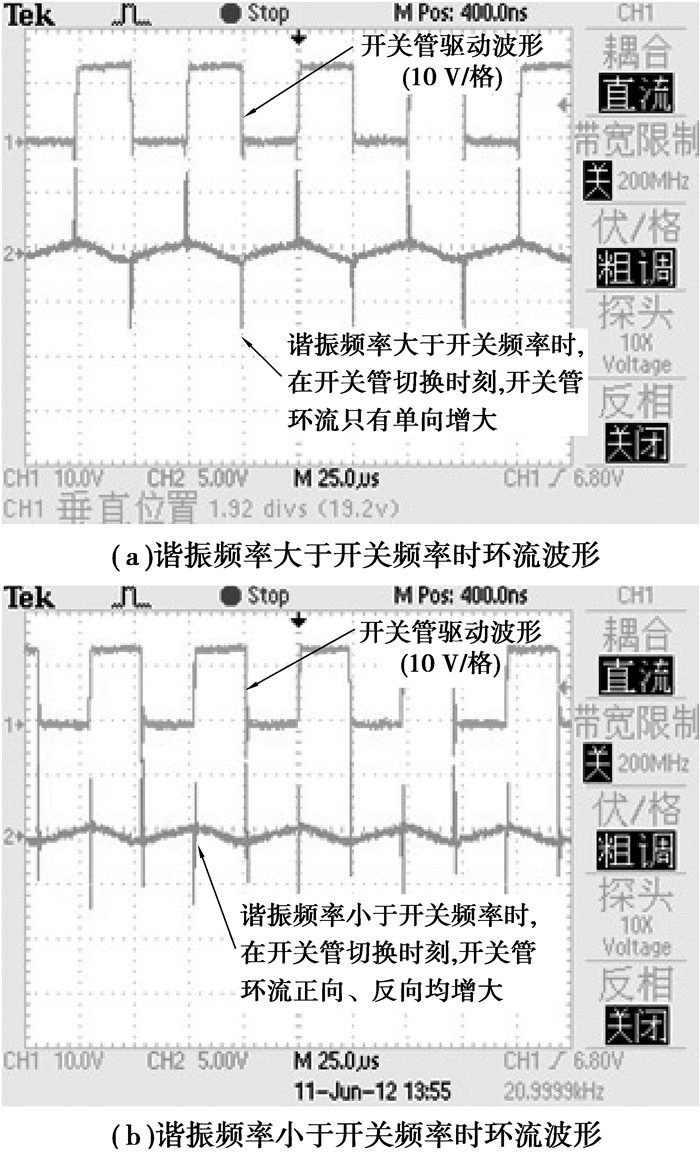
如图 6所示,在开关管每一次切换的时刻,当检测到开关管环流正向和反向均增大,此时谐振频率小于开关频率,需要开关频率进行负补偿(即减小开关频率)。当检测到开关管环流只有单向电流增大时则对开关频率进行正补偿(即增大开关频率)。
|
图 6 谐振频率发生变化时环流波形 |
| 表 1 仿真参数 |
|
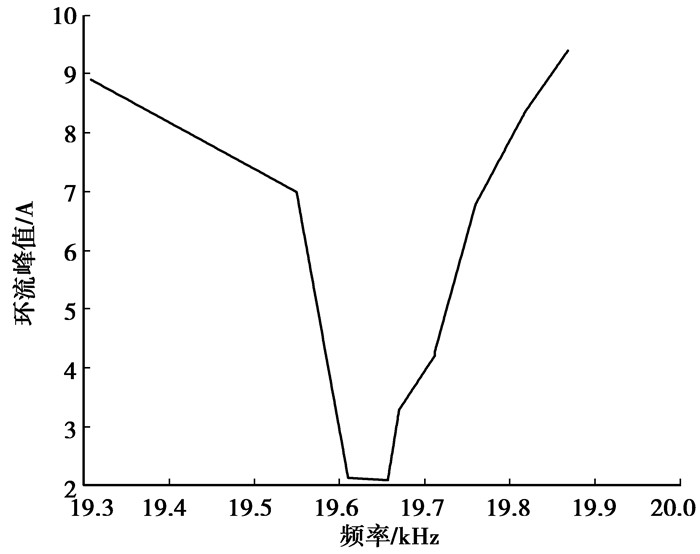
图 7 开关频率与环流峰值关系图 |
由图可以看出,随着开关频率的增加,环流峰值呈现出先下降后增大的变化趋势。
在进行开关频率补偿时,控制器可采用分段控制算法,当控制系统的环流峰值趋于增大时,加大控制力度进行环流抑制,即进入强控制段;而当环流峰值开始下降时,减弱控制力度进入弱控制段;同时,通过不断的检测环流峰值大小,改变控制器的控制力度,以适应变化的要求。
依据分段控制算法的基本控制思想,当检测到系统中不存在环流时(i=0,i为环流峰值大小),控制器工作于保持控制模态,即u(i)=u0。当检测到系统中存在环流时,即i≠0,根据环流峰值的大小进行分段控制,使得i→0。
1) 保持段
当环流峰值i=0时,控制器处于保持段。
| $ u\left( i \right) = {u_0}, $ | (1) |
式中:u为控制器输出函数,u0为控制器的前一状态输出[8]。
2) 弱控制段
当0 < i <
| $ u\left( i \right) = {u_0} \pm c, $ | (2) |
其中:em为系统能承受的最大环流峰值;c为常数(0.1 < c < 0.5)。
3) 强控制段
当
| $ u\left( i \right) = {u_0} \pm bc, $ | (3) |
式中b为比例系数(1≤b≤3)。
分段控制算法中各常数值是根据设计者的经验以及系统的精度要求来确定的[8]。
从前面的分析可知,可以采用同时检测开关管切换时刻、环流的大小和方向的方式对开关频率进行补偿,以保证其与谐振频率一致,使逆变器工作在谐振软开关状态下,抑制环流。
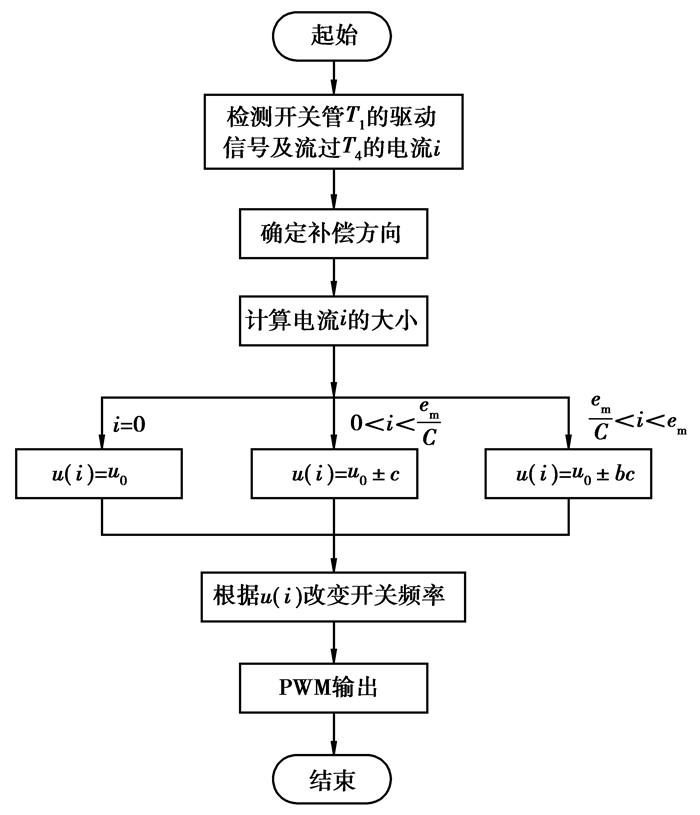
系统在开关管每一次切换时刻,采用电流互感器以及比较器进行环流及其峰值的检测,通过设定比较器的阈值大小与互感出的环流进行比较,确定环流峰值的范围。根据控制规律确定补偿方向,然后根据环流峰值的大小进行分段控制,按照控制器输出改变开关频率,使其逐步逼近谐振频率。下面以检测开关管T1的驱动信号以及测量流过T4中电流为例,进行控制系统的设计。控制流程图如图 8所示。
|
图 8 系统控制流程图 |
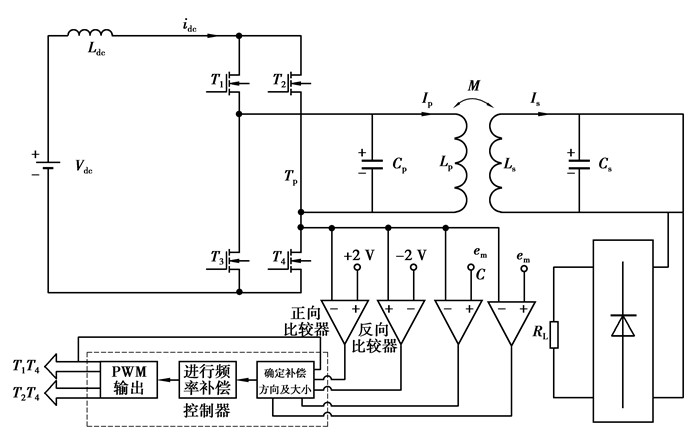
为验证控制系统和控制方法的可行性,取表 2所示参数,搭建硬件电路进行了验证,实验电路如图 9所示。
| 表 2 实验参数 |
|
图 9 实验系统结构图 |
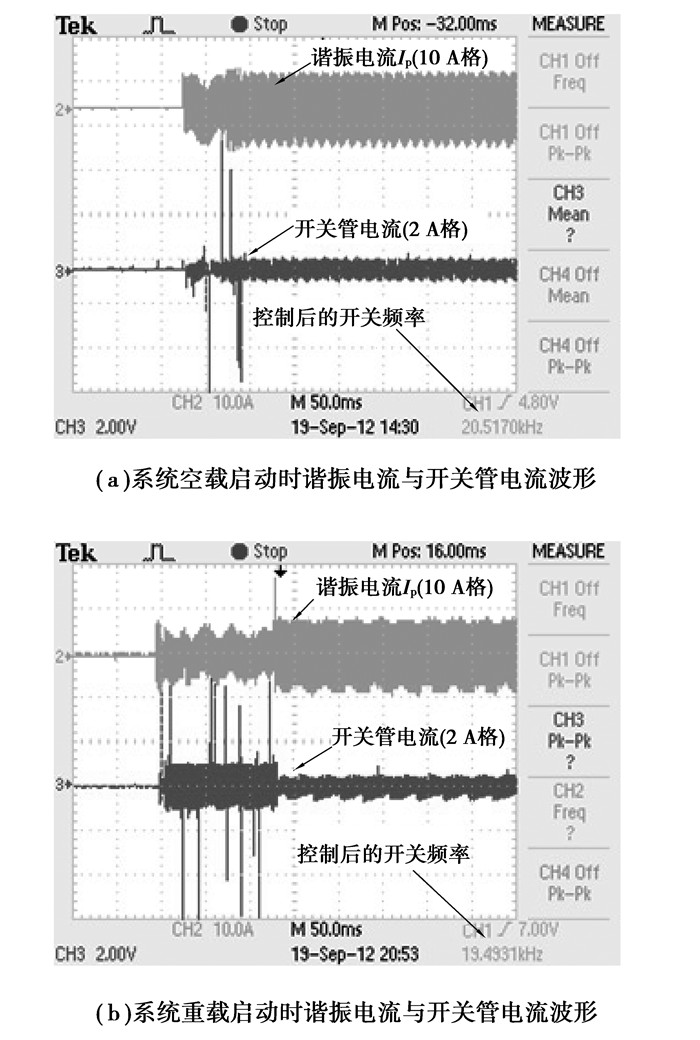
基于表 2的实验系统结构及实验参数,首先进行了系统启动控制实验。在实验中采取系统的空载启动以及带载启动,测量流过开关管电流大小,以验证控制方法是否能保持开关频率与谐振频率一致,从而抑制环流,测试结果如图 10所示。
|
图 10 系统启动时谐振电流与开关管电流波形 |
从图中可以看出,在系统刚开始启动时,控制系统还未来及响应,开关管中出现尖峰电流,当过了很短的一段时间后,控制系统调节开关频率与空载时的谐振频率(20.517 KHz)以及带载时的频率(19.493 2 KHz)一致,开关管电流中无尖峰存在。
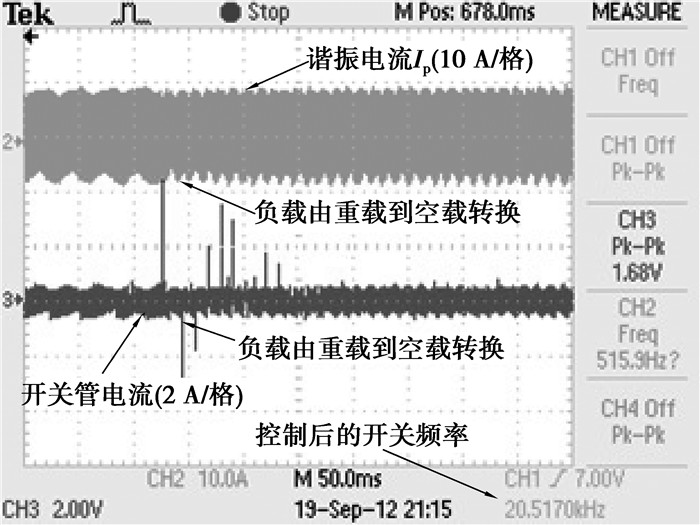
其次进行了负载突变控制实验。在带载稳态运行时,实现负载由带载到空载的跃变,测量流过开关管电流大小,以验证控制方法是否能调节开关频率与谐振频率一致,从而抑制环流,测试结果如图 11所示。
|
图 11 负载转换时谐振电流与开关管电流波形 |
从图中可以看出,控制系统响应迅速,调节开关频率与谐振频率一致,后稳态运行时开关管电流中无尖峰存在。
有上述实验结果来看,环流抑制系统针对负载扰动及突变,能够及时改变开关频率与谐振频率一致,从而达到抑制环流出现的效果。
4 结论开关管在谐振电容电压非零点切换导致了负载谐振型高频逆变器环流的产生。本文提出的实时检测环流方向及峰值大小,动态调节开关频率与谐振频率一致的控制方法,能够保证开关管在谐振电容电压过零点切换,较好的抑制环流。
| [1] | Hsu J U W, Hu A P, Swain A. A wireless power pickup based on directional tuning control of magnetic amplifier[J]. IEEE Transactions on Industrial Electronics, 2009, 56(7): 2771–2781. |
| [2] | Su Y P, Liu X, Hui S Y R. Mutual inductance calculation of movable planar coils on parallel surfaces[J]. IEEE Transactions on Power Electronics, 2009, 24(04): 1115–1123. |
| [3] |
戴欣, 孙跃, 苏玉刚, 等.
感应电能传输系统参数辨识与恒流控制[J]. 重庆大学学报, 2011, 34(06): 99–104.
DAI Xin, SUN Yue, SU Yugang, et al. Study on constant current control of inductive power transfer with parameter identification[J]. Journal of Chongqing University, 2011, 34(06): 99–104. (in Chinese) |
| [4] |
张凯, 潘孟春, 翁飞兵, 等.
感应耦合电能传输技术的研究现状与应用分析[J]. 电力电子技术, 2009, 43(3): 76–78.
ZHANG Kai, PAN Mengchun, WENG Feibing, et al. The study status quo and application analysis on the inductively coupled power transfer technology[J]. Power Electronics, 2009, 43(3): 76–78. (in Chinese) |
| [5] | Hu A P.Selected resonant converters for IPT power supplies[D].Auckland:The University of Auckland, 2000. https://www.researchgate.net/profile/Aiguo_Hu/publication/37984661_Selected_resonant_converters_for_IPT_power_supplies/links/555d104e08ae9963a112119d.pdf?inViewer=true&pdfJsDownload=true&disableCoverPage=true&origin=publication_detail |
| [6] |
孙跃, 王小霞, 戴欣, 等.
负载谐振型高频逆变器环流抑制技术[J]. 电工技术, 2009(02): 51–53, 56.
SUN Yue, WANG Xiaoxia, DAI Xin, et al. Circulating current inhibition technique of load resonant high frequency inverter[J]. electric engineering, 2009(02): 51–53, 56. DOI:10.3969/j.issn.1002-1388.2009.02.026 (in Chinese) |
| [7] | 张占松, 蔡宣三. 开关电源的原理与设计[M]. 北京: 电子工业出版社, 2004. |
| [8] |
孙跃, 陈国栋, 戴欣, 等.
非接触电能传输系统恒流控制策略[J]. 重庆大学学报, 2008, 31(7): 766–769.
SUN Yue, CHEN Guodong, DAI Xin, et al. A constant current control method for contactless power transmission systems[J]. Journal of Chongqing University, 2008, 31(7): 766–769. DOI:10.11835/j.issn.1000-582X.2008.07.012 (in Chinese) |
| [9] | Wang C S, Covic G A, Stielau O H. Power transfer capability and bifurcation phenomena of loosely coupled inductive power transfer systems[J]. IEEE Transactions on Industrial Electronics, 2004, 51(1): 148–157. |
| [10] |
苏玉刚, 唐春森, 孙跃, 等.
非接触供电系统多负载自适应技术[J]. 电工技术学报, 2009, 24(1): 153–157.
SU Yugang, TANG Chunsen, SUN Yue, et al. Load adaptive technology of contactless power transfer system[J]. Transactions of China Electrotechnical Society, 2009, 24(1): 153–157. (in Chinese) |
| [11] |
强浩, 黄学良, 谭林林, 等.
基于动态调谐实现感应耦合无线电能传输系统的最大功率传输[J]. 中国科学:技术科学, 2012, 42(7): 800–837.
QIANG Hao, HUANG Xueliang, TAN Linlin, et al. Achieving maximum power transfer of inductively coupled wireless power transfer system based on dynamic tuning control[J]. Sci China Tech Sci, 2012, 42(7): 800–837. (in Chinese) |
| [12] |
周雯琪, 马浩, 何湘宁.
感应耦合电能传输系统不同补偿拓扑的研究[J]. 电工技术学报, 2009, 24(1): 133–139.
ZHOU Wenqi, MA Hao, HE Xiangning. Investigation on Different Compensation Topologies in Inductively Coupled Power Transfer System[J]. Transactions of China Electrotechnical Society, 2009, 24(1): 133–139. (in Chinese) |
| [13] |
赵祖伟, 赵彩霞, 李贵强.
一种并联谐振型ICPT电路频率稳定性控制方法[J]. 微计算机信息, 2009, 25(5-2): 286–288.
ZHAO Zuwei, ZHAO Caixia, LI Guiqiang. A way of frequency stability control for the parallel resonant in ICPT system[J]. Microcomputer Information, 2009, 25(5-2): 286–288. (in Chinese) |
| [14] |
周雯琪, 马浩, 何湘宁.
基于动态方程的电流源感应耦合电能传输电路的频率分析[J]. 中国电机工程学报, 2008, 28(3): 119–124.
ZHOU Wenqi, MA Hao, HE Xiangning. Frequency analysis of a current source inductively coupled power transfer system based on dynamic circuit equations[J]. Proceedings of the CSEE, 2008, 28(3): 119–124. (in Chinese) |
| [15] |
杨民生, 王耀南.
感应耦合电能传输系统动态解谐传输功率控制[J]. 电机与控制学报, 2012, 16(1): 72–78.
YANG Minsheng, WANG Yaonan. Transferred power regulating method with a dynamically detuning inductor for ICPT pickups[J]. Electric Machines and Control, 2012, 16(1): 72–78. (in Chinese) |
| [16] |
邱峻.
其于遗传算法的特种齿轮传动系统优化设计[J]. 四川兵工学报, 2012(2): 68–70.
QIU Jun. Optimization design for special king of gear transimission system based on yenetic algorithm[J]. Journal of Sichuan Ordnance, 2012(2): 68–70. (in Chinese) |
 2013, Vol. 36
2013, Vol. 36

