2. 重庆市地质灾害防治工程技术研究中心, 重庆 400041;
3. 中国地质大学 工程学院, 武汉 430074
2. Chongqing Engineering and Technology Research Center of Geological Hazard Prevention and Treatment, Chongqing 400041, China;
3. Faculty of Engineering, China University of Geosciences, Wuhan 430074, China
边坡的破坏失稳是一个渐进累积的过程。在外部环境作用下,随着应力的升高,坡体内某些部分达到屈服,滑动面逐渐形成,直至完全贯通,随着塑性应变继续增大,边坡最终发生整体破坏。传统的分析方法不仅无法直接显示滑动面的发展过程,更不能定量显示滑面的受力、变形与破坏的过程。近年来,随着计算机技术的不断发展,采用有限元极限分析法分析边坡稳定性成为新的趋势[1-4]。其中,有限元强度折减法通过不断降低岩土强度,使边坡达到极限破坏状态,从而直接求出边坡的滑面位置与稳定安全系数,十分贴近工程设计,因此该方法得到了越来越广泛的利用。由于采用该方法能够直观、定量地模拟坡体内滑动面随稳定安全系数的降低到逐渐扩展直至贯通,以及边坡发生破坏的全过程,有助于提升人们对边坡的变形破坏机理的认识,从定性认识提升到可视、定量的认识,为边坡破坏模式的研究提供了新的思路[5-7]。笔者在前人的基础上,对边坡进行了分类,分类主要是依据岩土的性质与坡体的构造特征,因为它与岩土的变形破坏特征密切有关。依据分类对不同的边坡,给出不同强度折减系数(即不同稳定安全系数)下边坡的变形与滑面的塑性应变发展状况,从而显示边坡变形破坏的演化全过程。
1 边坡的分类边坡按不同的分类指标有多种分类,如按构成边坡的物质种类可以分为土质边坡、岩质边坡和岩土混合边坡3类;按边坡的高度可以分为一般边坡和高边坡两类;按边坡的工程类型可以分为路堑边坡、水坝边坡、露天矿边坡和建筑边坡等几类[8-10]。在众多分类方法中,与边坡变形破坏特征结合最紧密的通常是按边坡的物质种类和坡体的构造特征进行分类。其中,按物质种类可以分为土质边坡、岩质边坡和岩土混合边坡3类;按坡体的构造特征可分为:类均质边坡、层状边坡和软硬互层边坡3类。类均质边坡又可分为土质边坡与碎裂状和散体状岩石边坡;层状边坡可分为顺倾层状边坡(顺层边坡、溃屈边坡、双向顺层边坡和三维楔形体边坡)、反倾层状边坡(切层边坡和倾倒边坡);软硬互层边坡可分为上软下硬型(堆积层边坡、岩土二元边坡)和上硬下软型(软岩挤出边坡)。应当指出这里的层状既指层状岩体,也包括节理、裂隙、不连续面等结构面。由于边坡的稳定性很大程度上取决于坡体内结构面的状态、形状和空间分布,其组合形式不同,坡体的稳定性和变形破坏特征也各不相同,因此根据岩土的性质、坡体的构造特征和其主要破坏模式对边坡进行了分类(见表 1)。
| 表 1 边坡分类表及各类边坡对应的变形破坏特征与滑动面形态 |
有限元强度折减法通过不断降低边坡岩土体抗折的强度参数,直至达到极限破坏状态为止,此时的强度折减系数就是边坡的稳定安全系数。对于摩尔库伦材料,强度折减安全系数可表示为
| $ \tau = \frac{{c + \sigma \tan \varphi }}{\omega } = \frac{c}{\omega } + \sigma \frac{{\tan \varphi }}{\omega } = c' + \sigma \tan \varphi ' $ |
其中
这种强度折减安全系数的定义与边坡稳定分析的极限平衡条分法安全系数的定义是一致的,都属于强度储备安全系数。折减系数与边坡安全系数是相对应的,当折减系数等于1.00,即强度参数未折减时,得到的是自然状态下边坡的安全系数;当岩土体的强度在内、外因的作用下发生降低,即折减系数逐渐增大时,对应的安全系数也逐渐减小;当折减系数等于自然状态下的安全系数时,此时的安全系数等于1.00,坡体处于极限破坏状态。因此,可以采用有限元强度折减法对表 1中各类边坡处于不同安全系数状态下的变形特征和滑面形态进行研究。其中,岩体、结构面均采用理想塑性的摩尔库伦模型。通过网格变形示意图可以直观地显示坡体变形破坏的模式,根据塑性应变云图可以清楚地描述滑面随岩土体强度的降低逐渐扩展,直至破坏的全过程。
相关研究结果表明[11-12],当滑坡的稳定安全系数大于1.10时,滑坡处于稳定状态;当稳定安全系数在1.10~1.04之间时,滑坡处于欠稳定状态;当稳定安全系数在1.04~1.01之间时,滑坡处于严重欠稳定状态;当稳定安全系数在1.01~1.00之间时,滑坡处于不稳定状态,因此主要针对岩土体强度参数未折减时,以及岩土体强度参数折减后,坡体对应的稳定安全系数等于1.10、1.04、1.01时这4种稳定状态下坡体的变形破坏特征进行研究。
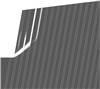
2.2 类均质边坡的破坏模式土质边坡与碎裂状和散体状岩石边坡均可视为类均质边坡。如表 1中所示类均质边坡,其岩土体容重γ=24 kN/m3,黏聚力c=145 kPa,内摩擦角φ=23°,采用有限元强度折减法对其变形破坏特征进行研究。从图 1可以看出,随着折减系数的增大,坡体沿圆弧型滑面发生明显的旋转滑动。图 1中塑性应变云图可以显示塑性区随着折减系数的增大逐渐形成至贯通的全过程。当安全系数接近1.04时,滑面贯通;当安全系数接近1.01时,塑性区的颜色进一步加深,表明塑性应变明显增大,坡体即将处于极限破坏状态。

|
图 1 类均质土边坡破坏特征示意图 |
1) 顺层边坡
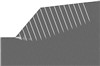
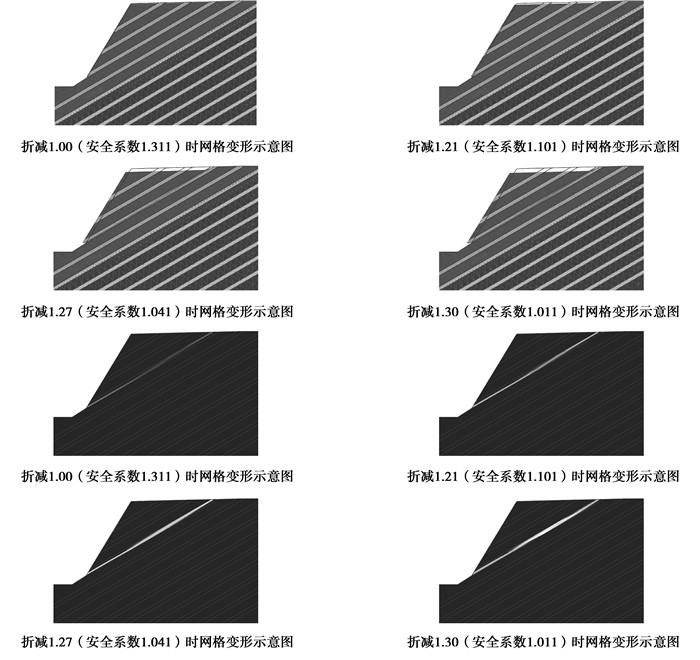
顺倾层状边坡如表 1中顺层边坡所示。其中,岩层倾角30°,岩体:容重γ=24.6 kN/m3,黏聚力c=1 100 kPa,内摩擦角φ=51°;结构面:容重γ=22 kN/m3,黏聚力c=100 kPa,内摩擦角φ=21°。同前所述,采用有限元强度折减法,根据得到的网格变形示意图和塑性应变云图可以看出,该类边坡破坏时主要是发生顺层面的滑动,如图 2所示。
|
图 2 顺层边坡破坏特征示意图 |
2) 溃屈边坡
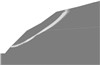
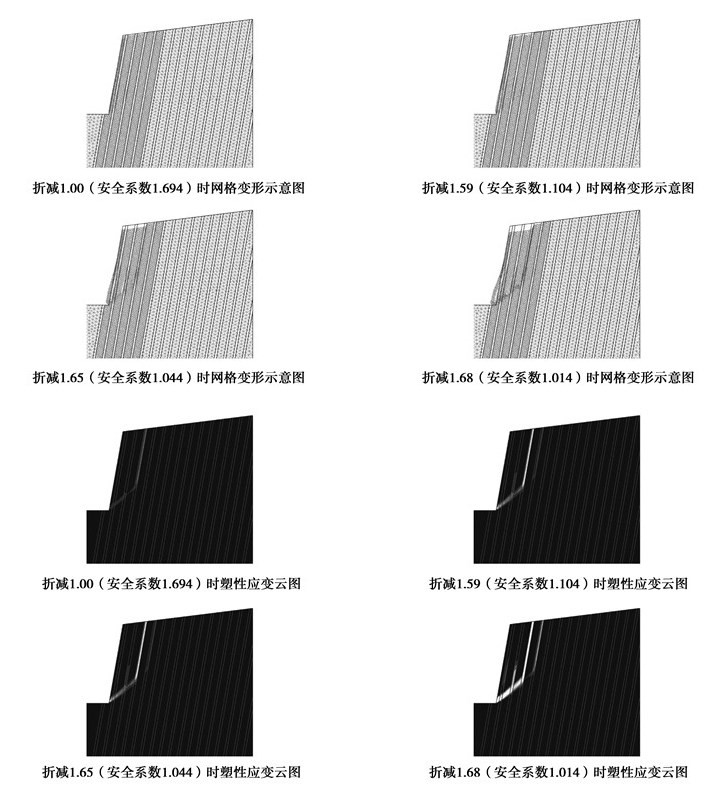
顺倾层状边坡,当岩层倾角较大时,常易发生溃屈、弯折破坏。如表 1中溃屈边坡所示,其中岩体:容重γ=24.6 kN/m3,黏聚力c=800 kPa,内摩擦角φ=36°;结构面:容重γ=24.6 kN/m3,黏聚力c=100 kPa,内摩擦角φ=21°。该类边坡由于滑移面未临空,下滑受阻,致使坡角附近顺层岩板承受纵向压应力,因此破坏时坡脚表部岩层会发生溃屈破坏,如图 3所示。
|
图 3 溃屈边坡破坏特征示意图 |
3) 双向顺层边坡
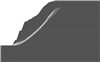
表 1中双向顺层边坡,岩体的容重γ=22 kN/m3,黏聚力c=1 100 kPa,内摩擦角φ=52°;结构面1倾角为13°,容重γ=22 kN/m3,黏聚力c=35 kPa,内摩擦角φ=15°;结构面2倾角为84°,黏聚力c=25 kPa,内摩擦角φ=13°,采用无厚度的接触单元模拟。由图 4所示双向顺层边坡的破坏特征示意图可以看出,该类边坡发生破坏时主要是岩体发生顺结构面的滑移,同时在后部结构面处发生拉裂。实际工程中,由于结构面的特征、形态的不同,其破坏形态也会有所不同。当双向顺层边坡2条结构面都比较平缓时,双向顺层边坡常发生剪切滑移破坏。

|
图 4 双向顺层边坡破坏特征示意图 |
塑性应变云图中,无法显示拉破坏,因此图 4中塑性应变云图在结构面2处未见贯通,其实已经形成拉剪贯通破裂面,这可由图 4中折减2.64(安全系数1.014)时网格变形示意图中看出,该类边坡主要发生多级滑动,滑面形状呈锯齿型。
4) 三维楔形体边坡
岩石力学中的楔形体稳定是一个典型的三维极限平衡分析问题,其破坏楔体是由2组或多组不同产状的结构面与临空面组合而成。如图 1所示楔形体边坡,其几何参数和物理参数如表 2所示。
| 表 2 楔形体算例几何参数 |
其中,岩体:容重γ=24.0 kN/m3,黏聚力c=1 100 kPa,内摩擦角φ=42°;结构面:容重γ=24.0 kN/m3,黏聚力c=120 kPa,内摩擦角φ=29°。结构面和岩体均采用实体单元模拟。同前所述,采用有限元强度折减法,根据得到的网格变形示意图和塑性应变云图(楔形体底部)可以看出,该类边坡破坏时主要发生三维楔形体沿结构面的滑动,如图 5所示。

|
图 5 三维楔形体边坡破坏特征示意图 |
1) 切层边坡
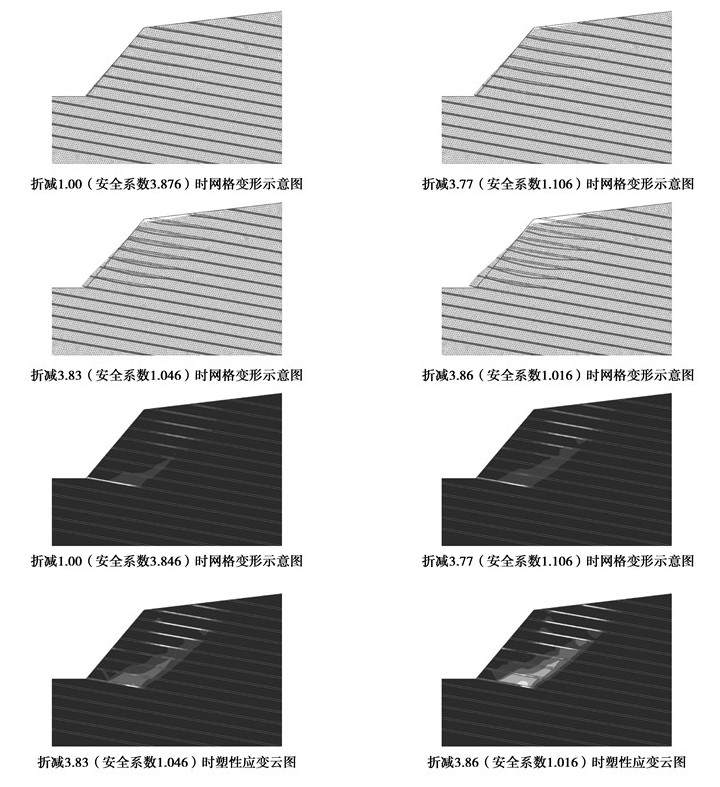
反倾层状边坡,当岩层倾角较小时,常易切层破坏。如表 1中切层边坡所示,其中,岩层倾角10°,岩体:容重γ=24.0 kN/m3,黏聚力c=1 100 kPa,内摩擦角φ=41°;结构面:容重γ=24.0 kN/m3,黏聚力c=100 kPa,内摩擦角φ=20°。该类边坡主要破坏形式为切层滑移与圆弧型旋转滑移相组合的破坏形式,形成近似圆弧型滑面,如图 6所示。
|
图 6 切层边坡破坏特征示意图 |
2) 倾倒边坡
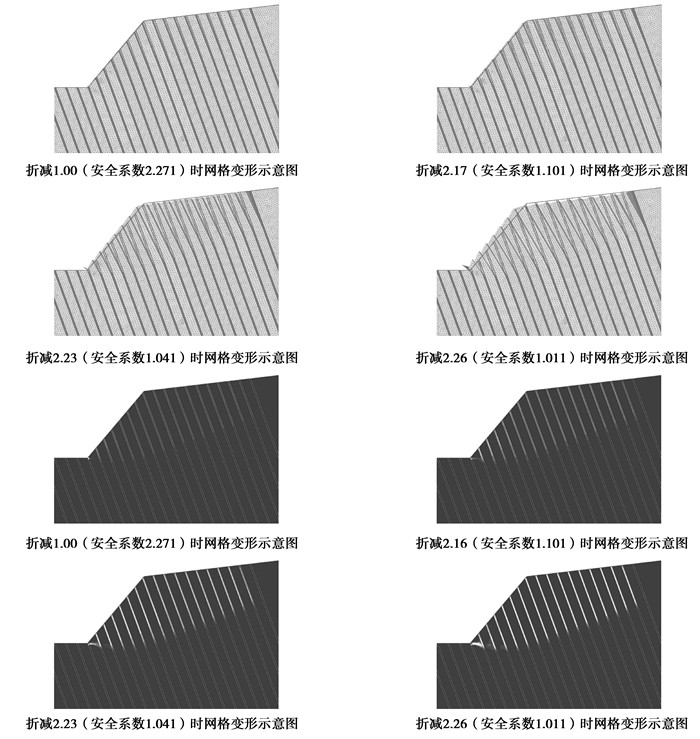
反倾层状边坡,当岩层倾角较大时,常易倾倒破坏。如表 1中倾倒边坡所示,岩层倾角70°,岩体:容重γ=24.0 kN/m3,黏聚力c=1 100 kPa,内摩擦角φ=41°;结构面:容重γ=24.0 kN/m3,黏聚力c=100 kPa,内摩擦角φ=20°。从图 7所示倾倒边坡的破坏特征可以看出,该类边坡由于岩层倾角较大,层状岩体产生向坡外的弯折变形,伴随坡面局部开裂,当主应力、剪应力超过岩体的抗折强度,发生折断破坏,引起边坡倾倒失稳。当倾倒边坡中存在多组结构面,特别是存在与反倾结构面斜交的结构面时,多组结构面切割形成的块体极易发生崩塌破坏。
|
图 7 倾倒边坡破坏特征示意图 |
1) 堆积层边坡
表 1中堆积层边坡,土体:容重γ=19.5 kN/m3,黏聚力c=22.4 kPa,内摩擦角φ=27°;岩体:容重γ=24.6 kN/m3,黏聚力c=1 100 kPa,内摩擦角φ=47°。采用有限元强度折减法可以得到该类边坡的变形破坏特征,如图 8所示。可以看出,由于上部堆积土的强度相对较低,因此该类边坡破坏时主要是上部发生旋转滑移,下部土体沿土岩分界面发生滑移破坏。

|
图 8 堆积层边坡破坏特征示意图 |
2) 岩土二元边坡
岩土二元边坡,岩体中存在软弱结构面,如表 1所示。土体:容重γ=19.5 kN/m3,黏聚力c=27 kPa,内摩擦角φ=24°;岩体:容重γ=24.6 kN/m3,黏聚力c=1 100 kPa,内摩擦角φ=47°;结构面:黏聚力c=70 kPa,内摩擦角φ=25°。由图 9可以看出,由于下伏岩体中存在强度相对较低的软弱结构面,此时下部岩体沿结构面发生滑动,上部土体沿土岩分界面发生旋转滑动,形成复合型滑面。

|
图 9 岩土二元边坡破坏特征示意图 |
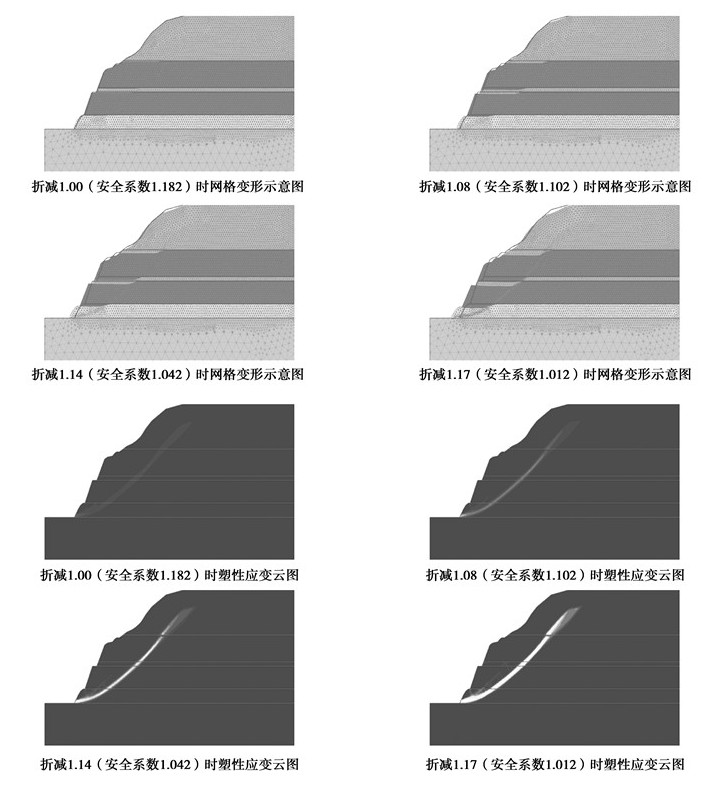
当上部硬层较厚,且下伏一定厚度的软岩,常易发生软岩的挤出变形。表 1中软岩挤出边坡,岩体1:容重γ=22 kN/m3,黏聚力c=150 kPa,内摩擦角φ°=31;岩体2:容重γ=25 kN/m3,黏聚力c=300 kPa,内摩擦角φ=32°;岩体3:容重γ=22 kN/m3,黏聚力c=120 kPa,内摩擦角φ=28°;岩体4:容重γ=22 kN/m3,黏聚力c=1 100 kPa,内摩擦角φ=41°。由于下伏软岩(岩体3)的强度相对较低,因此破坏时下伏软岩被挤出,形成圆弧状互动面,如图 10所示。
|
图 10 软岩挤出边坡破坏特征示意图 |
采用有限元强度折减法,根据计算得到的网格变形和塑性应变云图,可以直观地看到不同类型边坡的变形破坏特征,以及其滑面随稳定安全系数的降低逐渐扩展、贯通,直至破坏的全过程,从而为其有效防治提供依据。采用该方法进行边坡破坏机制的分析,有助于提升人们对边坡的变形破坏机理的认识,从定性认识提升到可视、定量、动态的认识,为边坡破坏模式的研究提供了新的思路。
| [1] | Zheng Y R, Deng C J, Zhao S Y, et al. Development of finite element limit analysis method and its applications in geotechnical engineering[J]. Engineering Sciences, 2007, 9(3): 10–36. |
| [2] | Zienkiewicz O C, Humpheson C, Lewis R W. Associated and non-associated visco-plasticity and plasticity in soil mechanics[J]. Géotechnique, 1975, 25(4): 671–689. DOI:10.1680/geot.1975.25.4.671 |
| [3] |
郑颖人, 赵尚毅.
岩土工程极限分析有限元法及其应用[J]. 土木工程学报, 2005, 38(1): 91–98.
ZHENG Yingren, ZHAO Shangyi. Limit state finite element method for geotechnical engineering analysis and its applications[J]. China Civil Engineering Journal, 2005, 38(1): 91–98. (in Chinese) |
| [4] | 郑颖人, 赵尚毅, 李安洪, 等. 有限元极限分析法及其在边坡中的应用[M]. 北京: 人民交通出版社, 2011. |
| [5] | Tamotsu M, San K C. Finite element slope stability analysis by shear strength reduction technique[J]. Soils and Foundations, 1992, 32(1): 59–70. DOI:10.3208/sandf1972.32.59 |
| [6] |
郑颖人, 赵尚毅.
有限元强度折减法在土坡与岩坡中的应用[J]. 岩石力学与工程学报, 2004, 23(19): 3381–3388.
ZHENG Yingren, ZHAO Shangyi. Application of FEM strength reduction in soil slope and rock slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(19): 3381–3388. DOI:10.3321/j.issn:1000-6915.2004.19.029 (in Chinese) |
| [7] |
郑颖人, 赵尚毅, 张鲁渝.
用有限元强度折减法进行边坡稳定分析[J]. 中国工程科学, 2002, 10(4): 57–61.
ZHENG Yingren, ZHAO Shangyi, ZHANG Luyu. Slope stability analysis by strength reduction FEM[J]. Engineering Science, 2002, 10(4): 57–61. (in Chinese) |
| [8] | 郑颖人, 陈祖煜, 王恭先, 等. 边坡与滑坡工程治理[M]. 北京: 人民交通出版社, 2007. |
| [9] |
殷跃平.
三峡库区边坡结构及失稳模式研究[J]. 工程地质学报, 2005, 13(2): 145–154.
YIN Yueping. Human-cutting slope structure and failure Pattern at the three gorges reservoir[J]. Journal of Engineering Geology, 2005, 13(2): 145–154. (in Chinese) |
| [10] |
黄润秋.
中国西南岩石高边坡的主要特征及其演化[J]. 地球科学进展, 2005, 20(3): 292–297.
HUANG Runqiu. Main characteristic of high rock slopes in southwestern china and their dynamic evolution[J]. Advances in Earth Sciences, 2005, 20(3): 292–297. (in Chinese) |
| [11] |
谭万鹏, 郑颖人, 王凯.
考虑蠕变特性的滑坡稳定状态分析研究[J]. 岩土工程学报, 2010, 32(Sup2): 5–8.
TAN Wanpeng, ZHENG Yingren, WANG Kai. Stable state of landslide considering creep properties[J]. Chinese Journal of Geological Engineering, 2010, 32(Sup2): 5–8. (in Chinese) |
| [12] |
谭万鹏, 郑颖人, 陈卫兵.
动态、多手段、全过程滑坡预警预报研究[J]. 四川建筑科学研究, 2010, 36(1): 106–111.
TAN Wanpeng, ZHENG Yingren, CHEN Weibing. Studies on the land-slope forecast and early warning by more means in full dynamic discourse[J]. Sichuan Building Science, 2010, 36(1): 106–111. (in Chinese) |
 2013, Vol. 36
2013, Vol. 36