2. 温州电力局, 浙江 温州 325000
2. Wenzhou Electric Power Bureau, Wenzhou, Zhejiang 325000, China
开发和利用安全、清洁、灵活的可再生分布式能源是减轻中国能源压力和保护环境的有效措施。光伏发电是其中潜力巨大的发电形式之一,与传统发电形式相比具有较强竞争优势[1-3]。绝大部分光伏发电属并网型,其接入将改变传统配电网的网络拓扑:从一个辐射式的网络变为一个遍布电源和用户互联的网络,配网可靠性评估模型也将相应发生变化。由于光照强度具有很强的随机性和间歇性,光伏发电系统接入电网后将带来很多不确定性因素[4],且并网型光伏发电系统由很多元件组成,而各组成部分皆可能故障导致系统功率输出的改变,因此若能综合考虑光伏发电系统外部环境变化和内部物理特性,即将外部光照强度的波动性和内部元件的故障失效模式有机结合建立光伏发电系统输出功率的概率模型,则能更准确地对含并网型光伏发电系统的配电网进行可靠性评估分析。
考虑光伏发电接入配电网的可靠性评估,国内外已有一些研究。文献[4]根据光伏发电系统的拓扑结构和光照资源的限制,建立了六状态可靠性模型,但研究对象局限于独立光伏发电系统,且对光伏发电系统故障后果划分较为粗略,所建模型很难准确评估其接入配电网后对配电网可靠性的影响。文献[5]采用解析法和模拟法分别给出了风电和光伏发电的多状态电源模型和时变负荷模型,但可靠性评估模型仅考虑了光照强度变化对系统可靠性的影响。文献[6]采用模拟法分析了天气对光伏发电系统元件的故障率和故障恢复时间的影响,但光伏系统的故障模式只考虑了系统完全失效,没有分析其部分失效模式及相应输出功率。
借鉴上述文献的优点和不足,笔者对含并网型光伏发电系统的配电网可靠性评估展开研究,考虑光伏发电系统各组成元件的可靠性和光照强度的波动性对输出功率的综合影响,并进一步分析光伏发电系统与配电网的互动影响,提出了光/柴混合发电系统接入配电网后对配电网可靠性影响的评估模型和算法。
1 光/柴混合发电系统电源模型配电网正常运行时,光/柴混合发电系统并网运行,与主电源一起共同为配电网各负荷点提供电力。当配电网主馈线故障时,在配电网内将形成一个小型自治电力系统—孤岛,孤岛成功运行的条件是岛内电源出力大于等于岛内负荷需求。受光照强度不确定性的影响,光伏发电的功率输出具有很强随机性和间歇性,而孤岛负荷也处于不断动态变化中[7],岛内可能频繁出现光伏发电和负荷功率不平衡的现象,导致频率偏移过大,孤岛失去稳定运行。为使孤岛频率可控,孤岛电源除光伏发电外,通常还需配置输出功率较稳定且调节的传统分布式电源,例如柴油发电机组,并通过其励磁或调速器控制使孤岛运行在频率可控制的范围内[8]。
1.1 计及光伏系统元件故障的输出功率概率模型光伏发电系统的输出功率与其元件故障情况和光照强度大小密切相关,元件故障和光照强度是彼此独立的随机事件,可分别计及其各自影响进行研究,然后再综合建模。本节首先研究光伏发电系统元件随机故障对输出功率的影响。
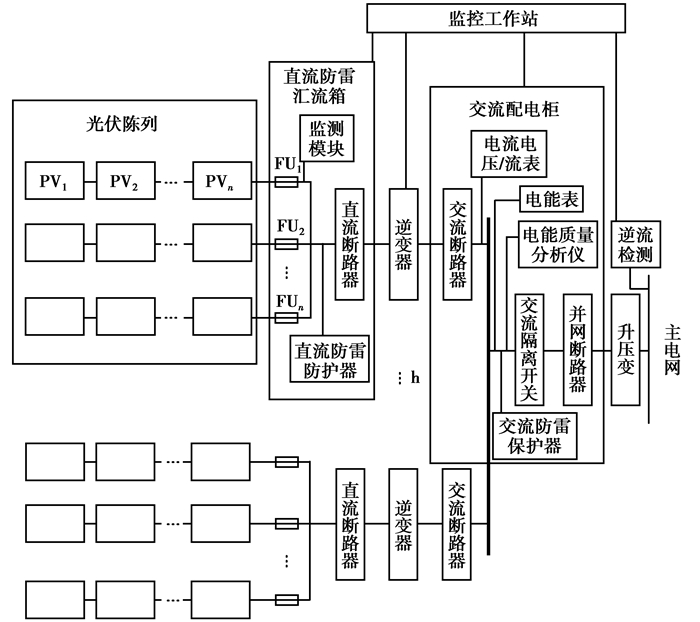
并网型光伏发电系统主要由光伏阵列、直流防雷汇流箱、逆变器、交流配电柜和升压变经串并联构成[9-10],整个系统的拓扑结构如图 1所示。
|
图 1 光伏发电系统结构图 |
由于光伏发电系统(PVS)的监测、保护和控制等二次设备失效的概率远低于一次设备,故可重点考虑PVS一次设备故障对输出功率的影响。根据元件串并联关系,将光伏发电系统划分为3个层次,第1层为光伏阵列-熔断器层;第2层为直流断路器-逆变器-交流断路器层;第3层为交流汇流母线-交流隔离开关-并网断路器-升压变层。
第1层设光伏电池模块和熔断器的故障率分别为λc和λf,平均故障修复时间分别为rc和rf。根据串并联系统可靠性指标计算公式[11],则光伏电池串故障率λ1、故障修复时间r1和无效度U1为
| $ {\lambda _1} = n{\lambda _{\rm{c}}} + {\lambda _{\rm{f}}}, $ | (1) |
| $ {r_1} = \frac{{n{\lambda _{\rm{c}}}{r_{\rm{c}}} + {\lambda _{\rm{f}}}{r_{\rm{f}}}}}{{{\lambda _1}}}, $ | (2) |
| $ {U_1} = {\lambda _1}{r_1}。$ | (3) |
第2层设直流断路器、逆变器和交流断路器的故障率分别为λdb、λI和λab,故障修复时间分别为rdb、rI和rab,则第2层元件故障率λ2、故障修复时间r2和无效度U2为
| $ {\lambda _2} = {\lambda _{{\rm{db}}}} + {\lambda _{\rm{I}}} + {\lambda _{{\rm{ab}}}}, $ | (4) |
| $ {r_2} = \frac{{{\lambda _{{\rm{db}}}}{r_{{\rm{db}}}} + {\lambda _{\rm{I}}}{r_{\rm{I}}} + {\lambda _{{\rm{ab}}}}{r_{{\rm{ab}}}}}}{{{\lambda _2}}}, $ | (5) |
| $ {U_2} = {\lambda _2}{r_2}。$ | (6) |
第3层设交流汇流母线、交流隔离开关、并网断路器和升压变的故障率分别为λb、λas、λgb和λT,故障修复时间分别为rb、ras、rgb和rT,则第3层元件故障率λ3、故障恢复时间r3和无效度U3分别为
| $ {\lambda _3} = {\lambda _{\rm{b}}} + {\lambda _{{\rm{as}}}} + {\lambda _{{\rm{gb}}}} + {\lambda _{\rm{T}}}, $ | (7) |
| $ {r_3} = \frac{{{\lambda _{\rm{b}}}{r_{\rm{b}}} + {\lambda _{{\rm{as}}}}{r_{{\rm{as}}}} + {\lambda _{{\rm{gb}}}}{r_{{\rm{gb}}}} + {\lambda _{\rm{T}}}{r_{\rm{T}}}}}{{{\lambda _3}}}, $ | (8) |
| $ {U_3} = {\lambda _3}{r_3}。$ | (9) |
第1层元件故障考虑至3阶,第2层考虑至2阶,第1、2层交叠故障考虑至3阶;第3层考虑至1阶。设i、j、k分别表示第1、2、3层元件故障阶数;i+j为1、2层组合故障阶数,则光伏发电系统无故障、部分故障和完全停运表示为
| $ \left\{ \begin{array}{l} 0 \le i \le 3,\\ 0 \le j \le 2,\\ 0 \le i + j \le 3,\\ 0 \le k \le 1,\\ i,j,k \in 整数。\end{array} \right. $ | (10) |
光伏发电系统与元件故障模式相对应的输出功率Pijk及其概率Uijk的数学模型为
| $ {P_{ijk}} = \left( {1 - k} \right)\frac{{\left( {h - j} \right)m - i}}{{hm}}{P_{\rm{r}}}\eta , $ | (11) |
| $ \begin{array}{l} {U_{ijk}} = \left( {1 - k} \right)C_{\rm{h}}^jU_2^j{\left( {1 - {U_2}} \right)^{h - j}}\\ \;\;\;\;\;\;\;\;\;C_{\left( {{\rm{h}} - j} \right)m}^iU_1^i{\left( {1 - {U_1}} \right)^{\left( {h - j} \right)m - i}} + k{U_3}, \end{array} $ | (12) |
式中:Pr为光伏发电系统的额定容量;η为逆变器的逆变效率,取η=0.95。
1.2 时变光照强度下光伏系统输出功率概率模型光伏系统输出功率不仅与其故障模式有关,还与光照强度密切相关。只考虑光照强度变化时的光伏系统输出功率模型可参考文献[2],取标准光照强度Is为1 000 W/m2;光电转换效率达到最大时的光照强度Kc =150 W/m2。
为降低计算复杂性,以年小时平均光照强度代替实际光照强度,将年光照强度值按100 W/m2的间距分成多组光照强度值,统计各组光照强度值一年中出现的小时数并计算其出现概率,年小时光照强度值及其概率采用文献[2]中的统计数据。
1.3 光伏系统功率输出概率模型将光伏系统的元件故障和光照强度IT变化下的输出功率P(IT)相组合,得出同时计及二者随机性的光伏系统输出功率Pijk(IT)及其概率Uijk(IT):
| $ {P_{ijk}}\left( {{I_{\rm{t}}}} \right) = \frac{{{P_{ijk}}}}{{{P_{\rm{r}}}}}P\left( {{I_{\rm{t}}}} \right), $ | (13) |
| $ {U_{ijk}}\left( {{I_{\rm{t}}}} \right) = {U_{ijk}}U\left( {{I_{\rm{t}}}} \right), $ | (14) |
式中U(IT)是光照强度为IT的概率。
1.4 光/柴混合发电系统输出功率模型本文中柴油发电机组作为备用电源,其可靠性模型采用“运行停运”两状态模型,设其强迫停运率为Ud,可用容量为Pd。采用离散卷积算法,得到光/柴混合发电系统的功率输出PDG及其概率UDG,其中x表示柴油发电机组运行状态,x=1表示正常运行,x=0表示故障停运。
| $ {P_{{\rm{DG}}}} = {P_{ijk}}\left( {{I_{\rm{t}}}} \right) + x{P_{\rm{d}}}, $ | (15) |
| $ {U_{{\rm{DG}}}} = {U_{ijk}}\left( {{I_{\rm{t}}}} \right) * \left[ {x\left( {1 - {U_{\rm{d}}}} \right) + \left( {1 - x} \right){U_{\rm{d}}}} \right]。$ | (16) |
研究所用负荷模型采用文献[12]中IEEERTS79可靠性测试系统的年小时负荷模型。当配电网主馈线故障时,光/柴混合发电系统及其周围负荷点与主馈线分离,按计划孤岛方式运行,因光伏系统输出功率和孤岛负荷的随机变化,孤岛电源可用出力与负荷相匹配的概率p为
| $ p = \sum\limits_{i = 1}^{8.736} {\left( {\sum\limits_{j = 0}^m {{p_{{\rm{DG}}j}}} } \right){p_{{\rm{L}}i}}} , $ | (17) |
式中:m为光/柴混合发电系统可用出力大于等于第i小时负荷需求的出力状态数;pDGj为其中第j个状态的发生概率;pLi为孤岛内第i个小时负荷出现的概率,且pLi=1/8 736。
3 孤岛负荷点可靠性指标计算公式 3.1 孤岛的修复域、隔离域和零域的定义根据孤岛外元件故障对孤岛影响的不同,将配电网划分为修复域、隔离域和零域,分别定义如下。
修复域。配电网某些区域的元件故障导致孤岛从脱网至重新并网所需时间为故障元件的修复时间,则这些区域称为修复域,用符号R表示。
隔离域。配电网某些区域的元件故障导致孤岛从脱网至重新并网所需时间为故障隔离时间,则这些区域称为隔离域,用符号I表示。
零域。配电网某些区域的元件故障不会影响到孤岛的并网运行,这些区域称为零域,用Z表示。
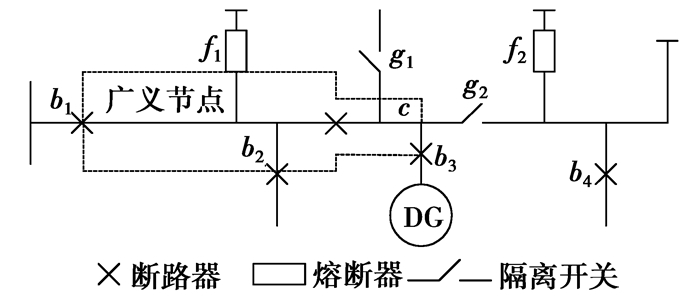
配电网中通常配置多个断路器和熔断器,故障发生时,不同位置断路器/熔断器拒动对孤岛的影响程度各异,按影响程度对其进行分级分类。首先给出上级断路器和下级断路器/熔断器的定义:从配电网中某断路器/熔断器所在位置逆潮流方向搜索,首遇断路器称为该断路器/熔断器的上级断路器,相应的,该断路器/熔断器称为此上级断路器的下级断路器/熔断器。断路器和熔断器分层概念如图 2所示。
|
图 2 1级断路器和熔断器的定位 |
将计划孤岛在主馈线上的并网点c与主馈线始端出线断路器b1之间的主馈线看成一广义节点,从该广义节点顺潮流方向展开广度优先搜索,在各个方向搜索到的首遇断路器(b2、b3、b4)或熔断器(f1、f2)称为1级断路器/熔断器。2级断路器/熔断器是1级断路器的相邻下级断路器/熔断器;类似可进一步归类为3级及以上的断路器/熔断器。为避免可靠性评估过于复杂,假设主馈线出线断路器b1完全可靠。
为计入断路器/熔断器拒动影响,给出如下定义:按前述修复域、隔离域和零域定义所得配电网区域划分,称为第1层修复域、隔离域和零域;设断路器/熔断器保护区域范围内元件故障时拒动,由上级断路器动作切除故障,按定义得到配电网区域划分,称为第2层修复域、隔离域和零域;设连续两级断路器/熔断器在保护区域范围内元件故障时拒动,按定义所得配电网区域划分,称为第3层区域。考虑连续两级保护断路器/熔断器同时拒动概率很小,本文算例分析只考虑至第2层区域划分。
3.2 孤岛负荷点可靠性指标计算公式当孤岛修复域或隔离域元件故障时,孤岛并网断路器跳开,由于光伏发电系统不能独自稳定运行,柴油发电机组快速启动,与光伏发电系统一起同期并网对孤岛负荷供电。当孤岛修复域、隔离域和孤岛内元件故障时,孤岛内第k个负荷点的停运率λk、平均故障恢复时间rk和年停电时间Uk为
| $ {\lambda _k} = \sum\limits_{j = 1}^{\left( {{N_{{{\rm{R}}_3}}} + {N_{{{\rm{I}}_3}}} + n} \right)} {{Q_j}{\lambda _j}} , $ | (18) |
| $ \begin{array}{*{20}{c}} {{U_k} = \left( {p\sum\limits_{j = 1}^{\left( {{N_{{{\rm{R}}_3}}} + {N_{{{\rm{I}}_3}}}} \right)} {{Q_j}{\lambda _j}} } \right){T_{\rm{s}}} + \left( {1 - p} \right)\left( {\sum\limits_{j = 1}^{{N_{{{\rm{R}}_3}}}} {{Q_j}{\lambda _j}{r_j}} + } \right.}\\ {\left. {\sum\limits_{j = 1}^{{N_{{{\rm{I}}_3}}}} {{Q_j}{\lambda _j}{T_g}} } \right) + \sum\limits_{j = 1}^n {{Q_j}{\lambda _j}{r_j}} ,} \end{array} $ | (19) |
| $ {r_k} = {U_k}/{\lambda _k}, $ | (20) |
式中:NR3、NI3和n分别表示孤岛的第3层修复域、隔离域和孤岛内的元件总数;λj和rj分别表示其中第j个元件的故障率和平均修复时间;Qj为熔断器或断路器的等效拒动概率,如果元件j位于主馈线出线断路器的主保护范围,则Qj=1,如果元件j位于1级断路器的主保护范围(j∈(R2-R1)),则Qj为该1级断路器的拒动概率;如果元件j位于2级断路器/熔断器的主保护范围(j∈(R3-R2)),则Qj为该2级断路器/熔断器及其上级断路器同时拒动的概率;对于孤岛内的元件,如果负荷点k与元件j处于同一熔断器或并网断路器的主保护范围或者元件j位于并网断路器的主保护范围,则Qj=1,否则,Qj取元件j的保护熔断器拒动概率;p为光/柴混合发电系统的输出功率与负荷相匹配概率,见式(17);Ts为光/柴混合发电系统成功启动所花时间,Tg为故障隔离时间。
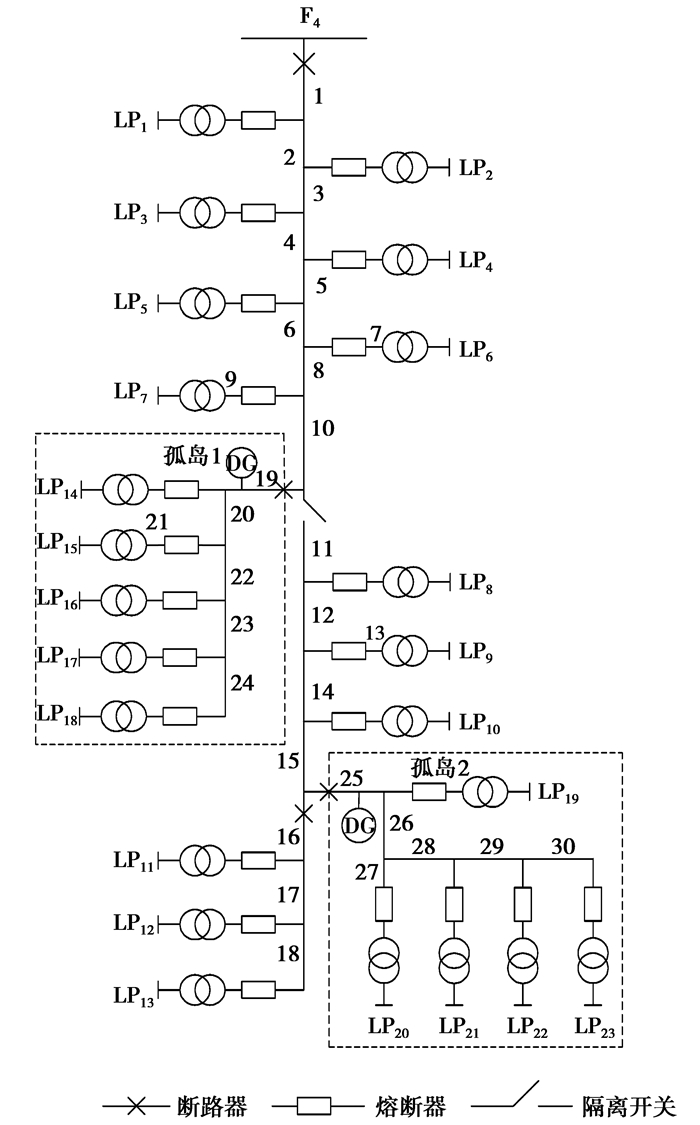
4 算例分析笔者采用IEEE-RBTS Bus6的主馈线F4开展可靠性评估分析,如图 3。线路参数和负荷点用户数见文献[13],配网元件可靠性参数见文献[14],光伏发电系统的元件可靠性参数见文献[9-15],假设断路器和熔断器拒动的概率为0.1,隔离开关操作时间Tg=1 h,孤岛成功运行所需时间Ts=0.1 h,柴油机组强迫停运率为0.05[5],每块光伏电池模块额定输出功率为230 W,每台逆变器交流侧额定功率为100 kW,年小时光照强度及其概率见文献[2]。
|
图 3 RBTS Bus6的主馈线F4 |
采用7种研究方案对不含和含有光伏发电系统的配电网展开可靠性评估分析。
方案1。对不含光伏发电系统的常规配电网可靠性评估,不考虑断路器和熔断器拒动的概率,按第1层区域划分思想划分。
方案2。与方案1不同之处是计及断路器和熔断器拒动的概率,按第2层区域划分思想划分。
方案3。不计光/柴混合发电系统故障,将光/柴总容量为孤岛峰荷的1.15倍且光/柴容量比为4:6[16]的混合发电系统接入孤岛1,计及断路器和熔断器的拒动概率。
方案4。与方案3不同之处是考虑光伏发电系统和柴油发电机组故障的可能性。
方案5。与方案4不同之处是将光/柴混合发电系统接入孤岛2。
方案6。与方案5不同之处是分多组光/柴容量比,分别是2:8、4:6、6:4、8:2。
方案7。考虑光/柴混合发电系统的随机故障,将其接入孤岛2,光伏发电容量为孤岛峰荷的100%,柴油发电机组容量分别为孤岛峰荷的20%、40%、60%、80%,计及断路器和熔断器的拒动概率。
对上述7个方案进行研究,计算出方案3~5孤岛电源出力与负荷相匹配的概率p分别为0.776 7、0.737 8、0.737 5,方案6、7孤岛电源出力与负荷相匹配的概率p如表 1,进一步得出每一方案5个典型负荷点和系统可靠性指标(LP16和LP21分别代表了孤岛1和孤岛2的负荷点),如表 2~5。
| 表 1 孤岛电源出力与负荷相匹配的概率p |
| 表 2 某些负荷点的停运率 |
| 表 3 某些负荷点的平均故障修复时间 |
| 表 4 某些负荷点的年停电时间 |
| 表 5 系统可靠性指标 |
1) 从方案1、2结果可见,方案2可靠性评估结果较方案1差,主要原因是:方案2计及了断路器和熔断器拒动,影响负荷点可靠性的区域为该负荷点第2层修复域和隔离域,而影响方案1负荷点可靠性的区域仅是该负荷点第1层修复和隔离域。
2) 从方案2、3的结果可见,配电网接入光/柴混合发电系统后,孤岛外负荷点可靠性指标没有变化,孤岛内负荷点除停运率不变外,其他可靠性指标和系统可靠性指标都得到明显改善。
3) 从方案3、4的评估结果和表 6可见,考虑光/柴混合发电系统自身的可靠性,计算出的孤岛电源出力与负荷相匹配的概率要略小于没有考虑时的计算结果,由此导致方案4的可靠性评估结果要差一些,但这种评估结果与实际更相符。
4) 从方案4、5的评估结果可见,在相同条件下,将光/柴混合发电系统接入孤岛2所得孤岛负荷点和系统可靠性指标要明显优于其接入孤岛1时的结果。其原因是:孤岛2较孤岛1远离变电站,未接入光/柴混合发电系统前,孤岛2的负荷可靠性差于孤岛1,而接入光/柴混合发电系统后,对孤岛1、2的负荷可靠性改善程度基本相同。
5) 由方案6可见,随光/柴容量比的提高,孤岛负荷点和系统可靠性指标变差,原因是光伏发电系统输出功率具有很强随机性,随光伏发电系统容量增加,将导致孤岛电源出力与负荷相匹配的概率大大减小,且光伏发电系统元件修复时间也较长。
6) 由方案7可见,随柴油发电机组容量增加,孤岛负荷点和系统可靠性指标均得到很好改善,是因为柴油发电机组功率输出较稳定且可调。将方案7、6的结果相比较,充分体现了光伏发电系统输出功率波动性和随机性对可靠性的不利影响。
5 结论提出了计及PVS失效模式与光照资源不确定性的PVS输出功率概率模型,采用光/柴混合发电多状态输出功率模型,建立了孤岛出力与负荷相匹配的概率数学模型。在配电网可靠性评估中,提出孤岛(负荷点)的修复域、隔离域和零域的概念,并计及断路器和熔断器拒动影响,提出分层思想。算例表明断路器和熔断器拒动对配电网可靠性影响很大;并网型光伏发电系统接入配网后,能较好改善孤岛负荷点和整个系统可靠性,但改善程度依赖柴油发电机组容量大小。
| [1] |
张改景, 龙惟定, 苑翔.
光伏发电系统的碳值分析[J]. 重庆大学学报, 2011, 34(11): 133–140.
ZHANG Gaijing, LONG Weiding, YUAN Xiang. Embodied-carbon analysis of renewable energy utilization system[J]. Journal of Chongqing University, 2011, 34(11): 133–140. DOI:10.11835/j.issn.1000-582X.2011.11.022 (in Chinese) |
| [2] | PARK J, WU L, CHOI J, et al. A Probabilistic reliability evaluation of power system including solar/photovoltaic cell generator[C]//Proceedings of 2009 IEEE Power And Energy General Meeting, July 26-30, 2009, Calgary, AB. Piscataway:IEEE Press, 2009:1-6. http://gala.gre.ac.uk/view/divisions/cms.default.html |
| [3] |
崔文智, 于松强, 廖全.
聚光型混合光伏光热系统热电性能分析[J]. 重庆大学学报, 2009, 32(1): 86–90.
CUI Wenzhi, YU Songqiang, LIAO Quan. Performance analysis of a concentrating solar hybrid photovoltaic-thermal system[J]. Journal of Chongqing University, 2009, 32(1): 86–90. DOI:10.11835/j.issn.1000-582X.2009.01.017 (in Chinese) |
| [4] |
王震, 鲁宗相, 段晓波, 等.
分布式光伏发电系统的可靠性模型及指标体系[J]. 电力系统自动化, 2011, 35(15): 18–24.
WANG Zhen, LU Zongxiang, DUAN Xiaobo, et al. Reliability model and indices of distributed photovoltaic power system[J]. Automation of Electric Power Systems, 2011, 35(15): 18–24. (in Chinese) |
| [5] | ATWA Y M, SAADANY E F, SALAMA M M A, et al. Adequacy evaluation of distribution system including wind/solar DG during different modes of operation[J]. IEEE Transactions on Power Systems, 2011, 26(4): 1945–1952. DOI:10.1109/TPWRS.2011.2112783 |
| [6] | CHA S T, JEON D H, BAE I S, et al.Reliability evaluation of distribution system connected photovoltaic generation considering weather effects[C]//Proceedings of 2004 International Conference On Probabilistic Methods Applied to Power Systems, September 12-16, 2004, Ames IA.Piscataway:IEEE Press, 2004, 451-456. |
| [7] |
孙瑜, BOLLENM, AULTG.
孤岛状态下含分布式电源的配电系统可靠性分析[J]. 电网技术, 2008, 32(23): 77–81.
SUN Yu, BOLLEN M, AULT G. Reliability analysis of island distribution systems with distributed energy resources[J]. Power System Technology, 2008, 32(23): 77–81. (in Chinese) |
| [8] | BAE I S, KIM J O. Reliability evaluation of distributed generation based on operation mode[J]. IEEE Transactions on Power Systems, 2007, 2(22): 785–790. |
| [9] | ZINI G, MANGEANT C, MERTEN J. Reliability of large-scale grid-connected photovoltaic system[J]. Renewable Energy, 2011, 36(9): 2334–2340. DOI:10.1016/j.renene.2011.01.036 |
| [10] | 李瑞生, 周逢权, 李燕斌. 地面光伏发电系统及运用[M]. 北京: 中国电力出版社, 2011. |
| [11] | 别林登R. 工程系统可靠性评估-原理和方法[M]. 周家启, 黄雯莹, 译. 重庆: 科学技术文献出版社重庆分社, 1988. |
| [12] | SUBCOMMITTEE P M. IEEE reliability test system[J]. IEEE Transactions on Power Apparats and Systems, 1979, 98(6): 2047–2054. |
| [13] | BILLINTON R, JONNAVITHULA S. A test system for teaching overall power system reliability assessment[J]. IEEE Transactions on Power Systems, 1996, 11(4): 1670–1676. DOI:10.1109/59.544626 |
| [14] | ALLAN R N, BILLINTON R, SJARIEF I, et al. A reliability test system for educational purpose basic distribution system data and results[J]. IEEE Transaction on Power Systems, 1991, 6(2): 813–820. DOI:10.1109/59.76730 |
| [15] | ZHANG P, WANG Y, XIAO W D, et al. Reliability evaluation of grid-connected photovoltaic power systems[J]. IEEE Transactions on Sustainable Energy, 2012, 3(3): 379–389. DOI:10.1109/TSTE.2012.2186644 |
| [16] | KARKI R, BILLINTON R. Cost-effective wind energy utilization for reliable power supply[J]. IEEE Transactions on Energy Convers, 2004, 3(2): 435–440. |
 2013, Vol. 36
2013, Vol. 36


