2. 重庆大学 电气工程学院, 重庆 400044
2. College of Electrical Engineering, Chongqing University, Chongqing 400044, China
电阻抗断层成像是一种只需对物体体表进行测量而重构出内部阻抗图像的技术。它通过注入电流到一个目标区域建立电场,随后对目标周边产生的电压进行测量[1]。传统的电阻抗断层成像技术中,电极的放置通常局限于某个平面,然而,电阻抗成像本质上是一个三维问题,其电流不局限于在某个平面上流动,因此,二维图像重建通常会产生伪像[2]。而三维电阻抗成像的主要问题是:系统无法负担复杂的算法,病态性使得算法有时难以实现,尤其是在边缘区域,最终造成重建图像中目标位置难以判断或形状扭曲[3]。在笔者前期的研究工作中,建立了开放式电阻抗成像系统,该系统能够很好地实现物体的表层阻抗判定,但是受制于探测深度的因素,精度只能保证在2~3 cm的范围内[4]。为此开发交叉平面电极阵列系统,通过交错的二维成像数据,能够更有效地构建三维成像模型,并在保证有效精度的前提下减小了直接三维重构的计算量。
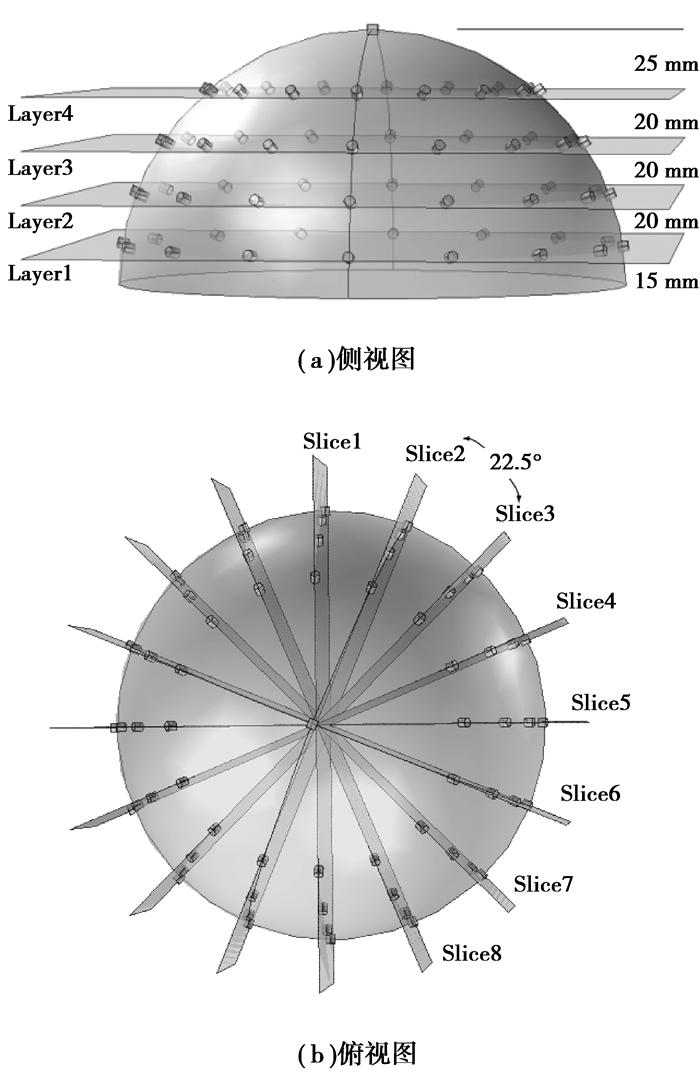
1 数值模型及方法 1.1 模型结构笔者构建的模型是一个半径为100 mm的半球,水平方向看,电极被分布在了4个不同的层上,每层的16个电极等间距环状地分布在半球的边缘(图 1(a)),该分布方式的良好对称性可以提供精确可靠的测量结果。模型的第1层距底部15 mm,之后的每一层间隔为20 mm。图 1(b)为该模型的俯视图,其中顶部的电极作为共用电极,65个电极又在空间上被分为8组垂直于上述的4组水平电极阵列。通过这样的划分,每个弧形切面包含9个电极,当电极从轴向注入模型时,电极之间的角度是不等的,但呈轴向对称。弧形电极的检测方式是基于电阻抗成像对腹腔内的出血的检测[5],虽然使用弧形电极阵列能够提供更多的有效信息,但是其注入电流在被测物体中的分布具有很大的不对称性,因此需要对算法进行评估,确定适当的算法参数。
|
图 1 电极放置模型 |
由于测量结果需要包含足够的、可重构的数据来进行稳定的图像重建,目前最常用的有“相邻”和“相对”驱动,它们都使用差分方式,对非电流注入电极进行测量,以减少电极的接触阻抗的影响,提高共模噪声抑制[6]。为此,对4层圆电极阵列采取相对电极注入,从而提高在中心区域的灵敏度,对8组弧形电极采取相邻电极注入,以提供更好的分辨率以及更多的独立的测量数据。
1.3 重构算法时差成像由测量导电率随时间的微小变化而进行的图像重构,这种方式能够提高重建图像的稳定性,克服如未知的接触阻抗、电极位置不准确和非线性所带来的问题。对边界电压V的测量,实际上是与电导率分布相关联,表述为V=f(σ)。通过泰勒级数展开,忽略高阶项,得到一个线性近似ΔV=S·Δσ,Δσ是矢量离散电导率,S为灵敏度矩阵。通过计算在时间间隔(t1,t2)上的ΔV=V2-V1,来得到电导率分布。
由于该系统几何结构及电极分布方式相比圆周的电极放置在重构中呈现出更高的病态性,因此,选定一个合适的算法和确定相关参数的取值尤为重要。在下面的实验中,笔者通过3种方法比较,来评估最适合的重建算法,以满足交叉平面电极图像重建的要求。
1.3.1 一步牛顿法(NOSER)一步牛顿法的应用首先由Cheney等提出[7]。该算法基于牛顿法,但只计算牛顿法的第一步,而不进行迭代计算。使用电阻率ρ来解释这个概念,在最小二乘法中,通过最小误差平方和估计,得到近似解:
| $ \arg \min \left\| {\Delta V - U\left( \rho \right)} \right\|_2^2。$ | (1) |
在一步牛顿法中,算法表达为
| $ \Delta \sigma = {\left( {{\mathit{\boldsymbol{J}}^{\rm{T}}}\mathit{\boldsymbol{J}} + \varepsilon \cdot {\rm{diag}}\left( {{\mathit{\boldsymbol{J}}^{\rm{T}}}\mathit{\boldsymbol{J}}} \right)} \right)^{ - 1}}{\mathit{\boldsymbol{J}}^{\rm{T}}} \cdot \Delta V, $ | (2) |
式中:J为雅可比矩阵,也称为灵敏度矩阵;ε是正规化参数,范围在0和1之间;diag(JTJ)表示对角矩阵,可看作是高阶误差的近似表达[8]。
1.3.2 加权最小范数法(WMNM)由于远离电极处的灵敏度通常较小,该算法最小二乘解基于最小化加权范数的解[9]。这种方法能够很好适应电阻抗成像中各电极拓扑结构和远点处的图像重建问题。Clay和Ferree提出的单步反演FOCUSS算法用于电阻抗图像重建中,称为加权最小范数法(WMNM)[10]。该算法中,加权系(wj)被定义为
| $ {w_j} = {\left( {\sum\limits_{i = 1}^M {J_{ij}^2} } \right)^{ - 1/2}}, $ | (3) |
通过对矩阵元素的规范化调整,可以使用一个对角加权矩阵W来表示,最终得到
| $ \Delta \sigma = \mathit{\boldsymbol{W}}{\left( {\mathit{\boldsymbol{JW}}} \right)^ + } \cdot \Delta V, $ | (4) |
可以得出,该变化实际上是重建矩阵J,使之扩展为W(JW)+。
1.3.3 Tikhonov正则化(TR)Tikhonov正则化算法在重建过程中应用高阻尼特征向量模型参数,添加罚函数使算法生成的阻尼效果,从获得稳定的解,同时在一定程度上确保平均时间内的空间分辨率。通常Tikhonov正则化,可以通过求解如下方程的最小范数解得到,
| $ \arg \min \left\{ {\left\| {\Delta V - U\left( \rho \right)} \right\|_2^2 + \lambda \left\| {\mathit{\boldsymbol{L}}\left( {\sigma - {\sigma _0}} \right)} \right\|_2^2} \right., $ | (5) |
对于零阶Tikhonov正则化,L是单位矩阵,参量σ0=0。
方程(5) 的代数形式为
| $ \Delta \sigma = {\left( {{\mathit{\boldsymbol{J}}^{\rm{T}}}\mathit{\boldsymbol{J}} + \lambda \cdot {\mathit{\boldsymbol{W}}^{\rm{T}}}\mathit{\boldsymbol{W}}} \right)^{ - 1}}{\mathit{\boldsymbol{J}}^{\rm{T}}} \cdot \Delta V。$ | (6) |
选择合适的正则化参数λ对于平衡该方程非常重要。W是一个正定矩阵,与先验信息密切相关,受噪声ΔV影响,一般是未知的。使用L-曲线法,可以选择适当的正则化参数[11]。
定义的参数η和ρ为
| $ \eta = lg{\left\| {\Delta \sigma } \right\|^2},\rho = \lg {\left\| {\mathit{\boldsymbol{S}}\Delta \sigma - \Delta V} \right\|^2}。$ | (7) |
L曲线的曲率可以表示为
| $ \kappa = 2\frac{{\rho '\eta '' - \rho ''\eta '}}{{{{\left[ {{{\left( {\rho '} \right)}^2} + {{\left( {\eta '} \right)}^2}} \right]}^{3/2}}}}。$ | (8) |
而正则化参数即为该曲线拐点处的值,正则化参数可以看作是通过加权罚项对最小范数方程平滑求解,即一奇异值过滤器[12]。
2 仿真分析该模型通过COMSOL Multiphysics 4.1建立三维模型,并进行仿真验证。数据分析、参数评估和图像重建在Matlab(版本:7.11.0) 中进行。
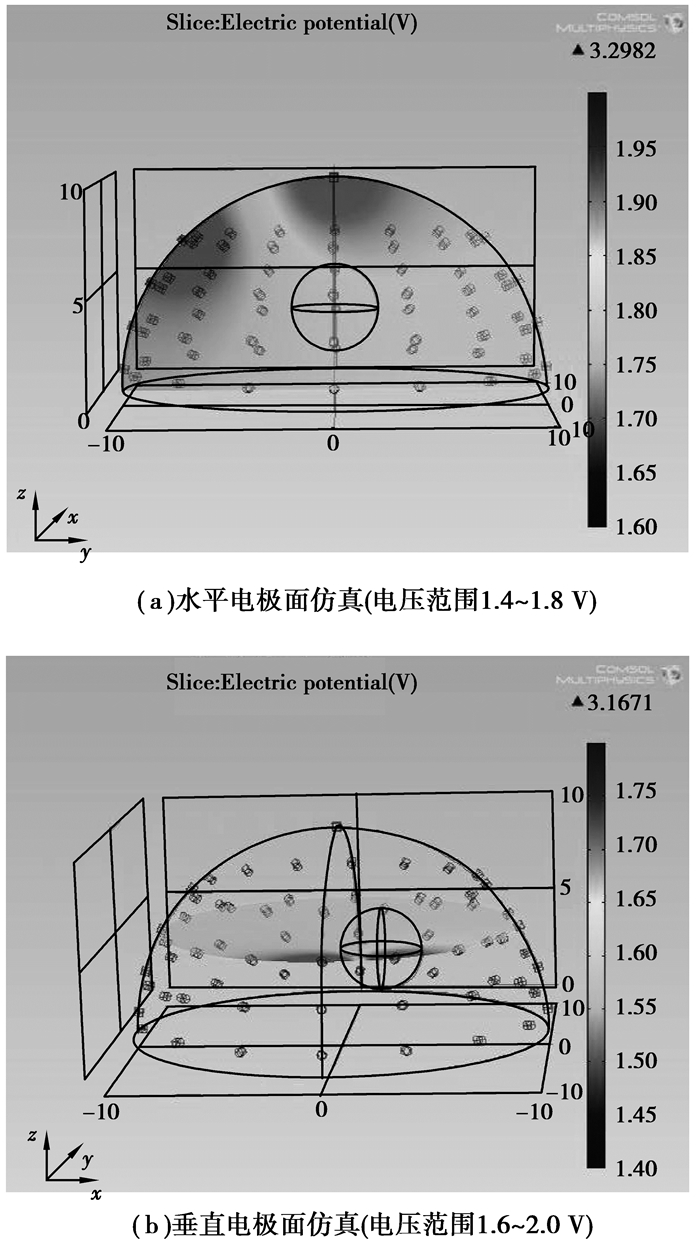
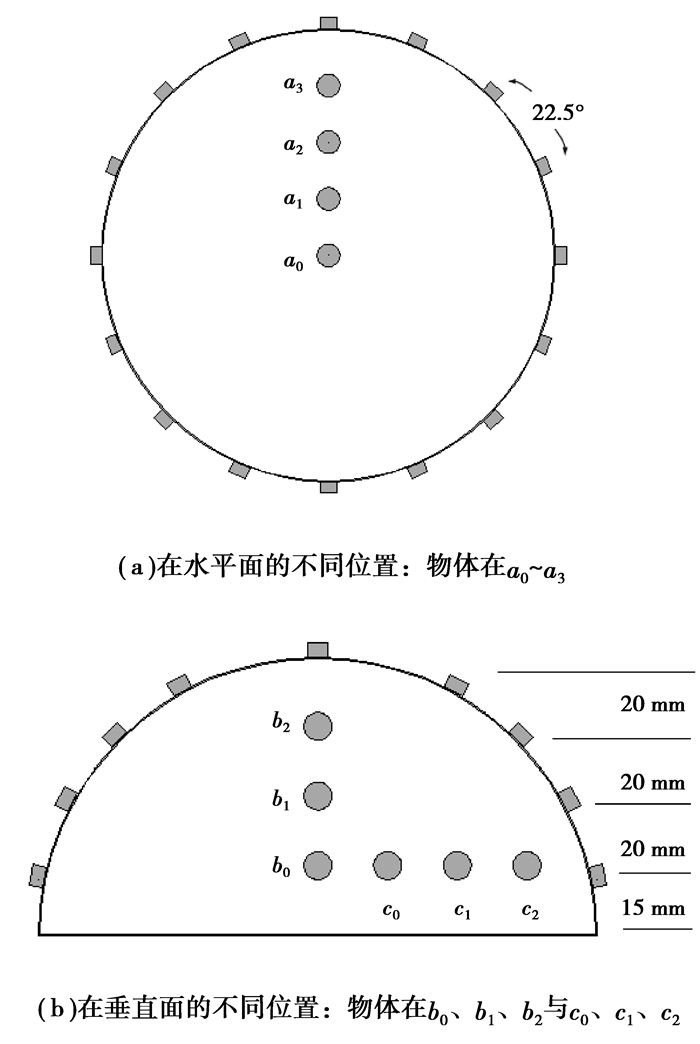
2.1 正问题仿真在图 2中,半球的半径为10 cm,容器内液体的电导率为0.2 S/m-1,电极(导电率6×107 S/m-1)为半径2 mm、高度4 mm的圆柱体,并部分插入到半球体内(电极分布参见1.1)。异物是一个电导率为0.3 S/m-1,半径为2 cm的球形物体,依次放置在0、2.5、5.0、7.5 cm,即图 3(a)标示为a0、a1、a2、a3处,进行水平切面仿真实验。依次放置在x=0 cm,y在2.5、5.0、7.5 cm,即图 3(b)标示为b0、b1、b2处;y=2.5 cm,x在2.5、5.0、7.5 cm,即图 3(b)标示为c0、c1、c2处,进行垂直切面仿真实验。因此,共有10个模拟仿真,分别对应于水平和垂直剖面的不同物体放置。仿真采用5 mA,频率为100 kHz的电流激励(激励和电压测量方式参见1.2)[13]。
|
图 2 正问题仿真 |
|
图 3 异物存在于不同位置的仿真 |
重构采用了有限元网格的方法,水平剖面包括10 728个元素,4 787个节点;垂直剖面包括5 461个元素,2 476个节点。两个网格模型与上述几何模型相匹配,容许公差设置为1×10-5,最佳正规化参数λ经计算分别为1.7×10-4和2.3×10-4。将测量数据整理为两组:a0~a3的数据作为水平面成像结果的评估;b0~b2和c0~c2的数据作为垂直面成像结果的评估。
2.3 仿真结果通过对比上述算法,对其在该模型中的表现加以评估。
1) 条件数(cond)。
对于矩阵H的SVD其分解的形式为
| $ \mathit{\boldsymbol{H}} = \mathit{\boldsymbol{U}}\sum {{\mathit{\boldsymbol{V}}^{\rm{T}}}} = \sum\limits_{i = 1}^N {{u_i}{\sigma _i}v_i^{\rm{T}}} , $ | (9) |
其中,U和V是正交列的矩阵。σi按降序排列,这样σ1≥…≥σn≥0,σi为H的奇异值。H的条件数cond(H)=σ1/σn。条件数提供了一种方法来衡量H对噪声的敏感性,相对较大的条件数,会使问题的病态性增强。
从表 1中可以看出,由水平面电极相关方程得到的条件数远小于垂直面的条件数,这是由于水平面是16个完整的圆状电极阵列,而垂直面为9电极的弧形阵列。由加权最小范数法所得的条件数略小于一步牛顿法,而Tikhonov正则化为三者中最小。此外,二维重建的条件数远比三维重建的条件数要小,通过该二维图像重构来获得空间位置的方法也比直接三维重构可靠性相对较高,通常三维重构中条件的值一般都大于1×104。
| 表 1 在两种电极排列方式下雅阁比矩阵的条件数比较(对于圆形分布取ε=0.5,λ=1.7×10-4,对于弧形分布取λ=2.3×10-4) |
2) 数量指数(Q)。
数量指数,通常也可看作图像指数,用于评估范围内由于异物引起的电导率相对变化。
| $ Q = \sum\limits_{i = 1}^N {{A_j} \cdot \Delta {\sigma _j}} , $ | (10) |
电导率变化和有限元单元分别表示为Δσi和Aj,定义相对数量指数为
| $ \delta Q = Q/{Q_0}, $ | (11) |
Q表示电导率变化测量值,Q0表示异物的真实电导率。
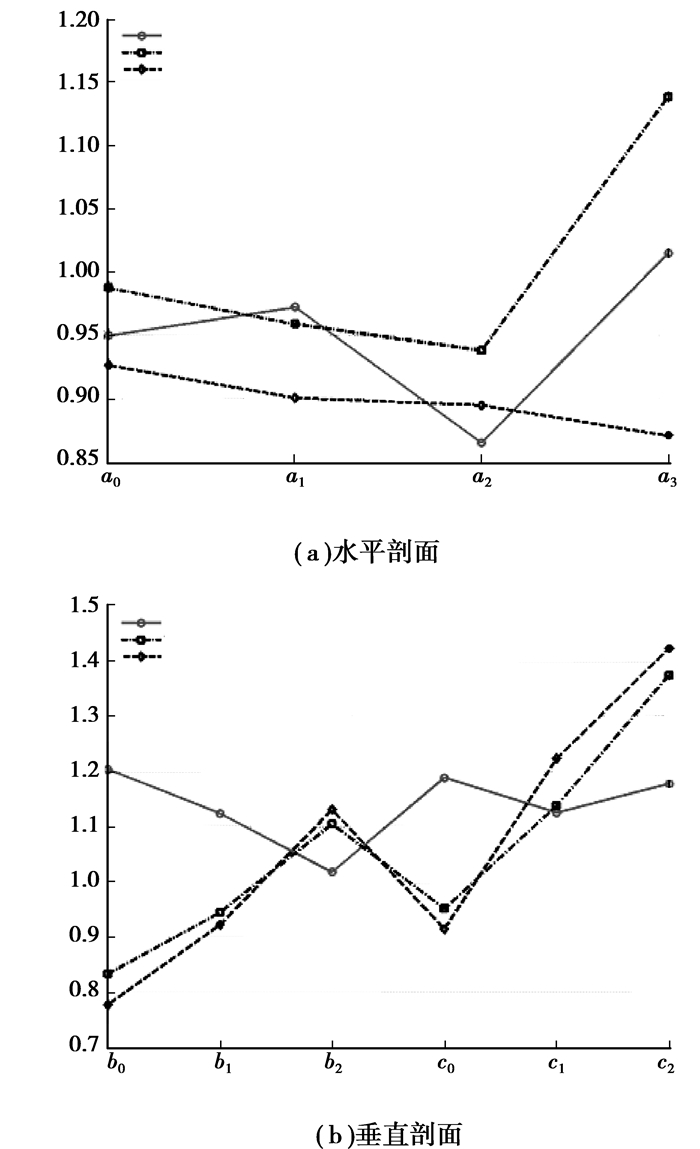
由图 4可以看出,对于3种算法的相对数量指数在不同位置处,都在理论值1左右波动,最大值约为1.4出现在c0处,NORSER和WPI算法在该位置的值相近。该数值在靠近成像范围的中心时,其大小接近理论值1。从结果还可以得出,当物体在c0、c1、c2位置时,重建结果的误差水平相对较高,而Tikhonov正则化的波动相对较小,特别是在电极阵列不完备的半圆形区域图 4(b)的几个位置中。
|
图 4 相对数量指数仿真结果 |
3) 分辨率(R)。
分辨率用于评估重建图像的集中程度,当有限单元的值超过成像范围内最大值的一半,该点即被定义为半幅值集。而分辨率定义为半幅值集之和与成像范围内所有值之和的比值再开方,即
| $ R = \sqrt {{A_{{\rm{HA}}}}/{A_{\rm{0}}}} 。$ | (12) |
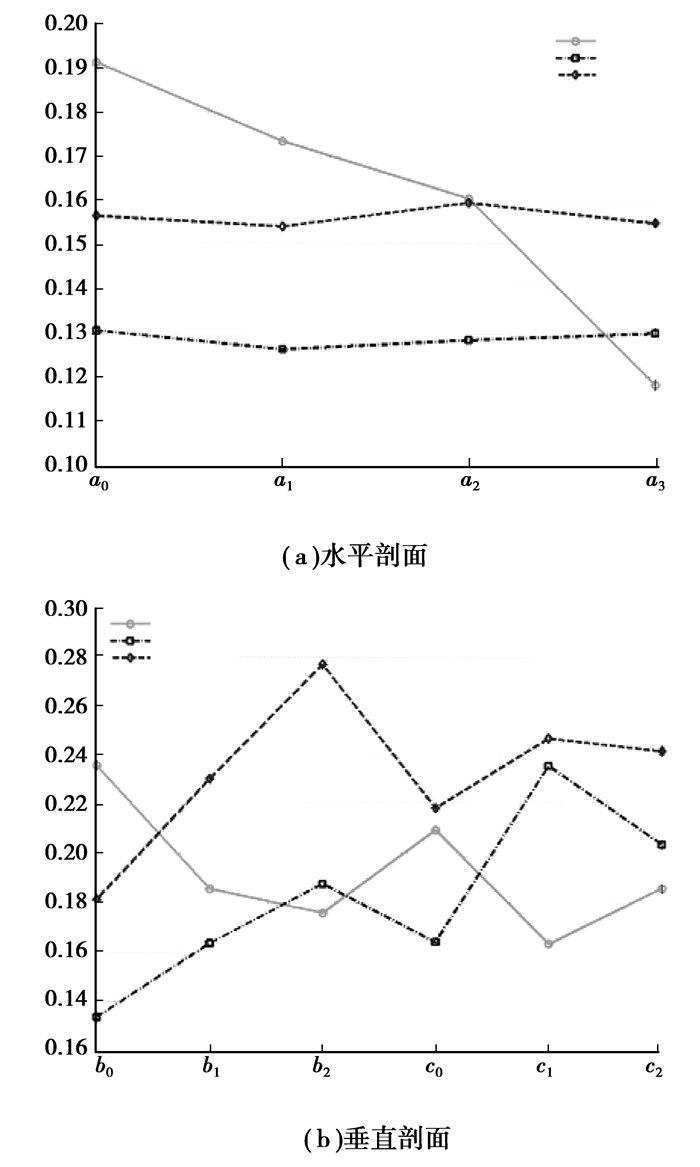
从以上定义可以看出,分辨率值较小代表成像区域会更清晰,重建图像整体而言会更加清晰。
图 5表明,在水平剖面的分辨率值相对较小也比较稳定,而Tikhonov正则化在中心区域比其他两种大,在边缘处较小,由于Tikhonov正则化加入了阻尼特征向量,物体在中心处的分辨率相对较差。从图 5(b)可以看出,对于垂直剖面的不完备电极阵列,分辨率的值相对较大,由于电极放置而导致的重构失真增强。
|
图 5 分辨率仿真结果 |
4) 位置误差(P)。
异物在成像区域内的位置被定义为
| $ P = \sum\limits_m {{\sigma _m}} \cdot {p_m}/\sum\limits_m {{\sigma _m}} , $ | (13) |
式中:pm为异物有限元单元的位置(xm,ym);σm为异物电导率值。
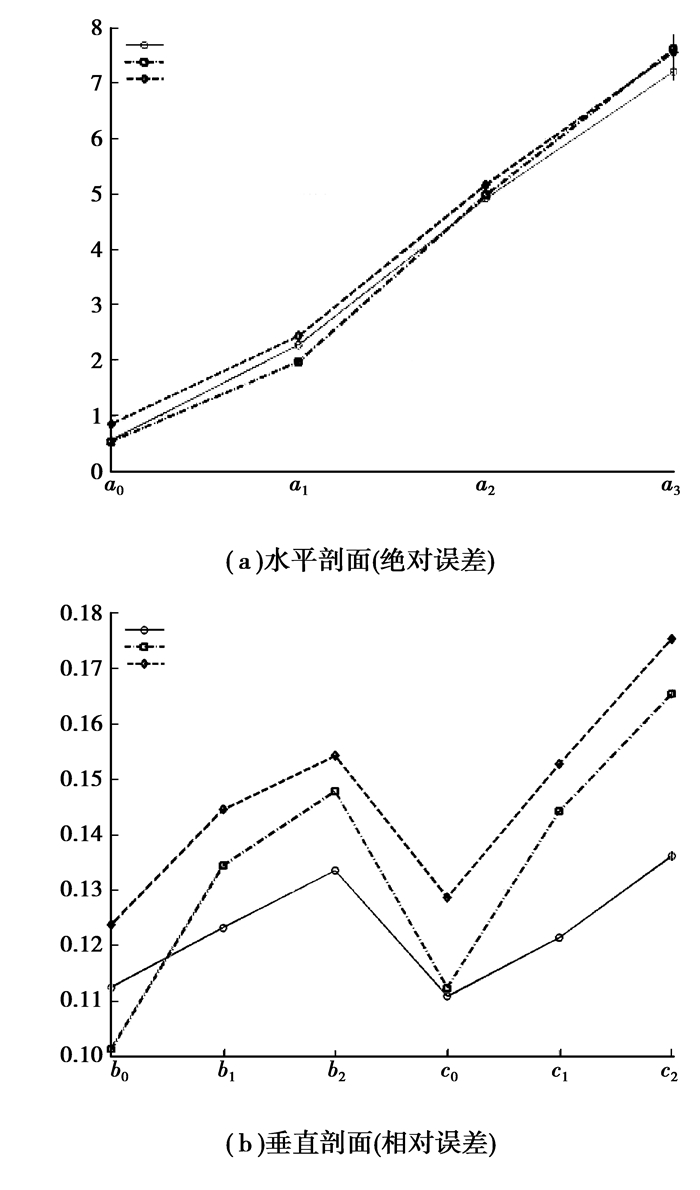
较小的位置误差,表明重建图像的异物位置更接近于目标实际位置的中心。
从图 6(a)可以看出其近似一条直线,其位置误差在水平剖面的完备电极阵列中不明显,错误率不应该是完整的圆,在所有地区。对于在垂直剖面的位置误差用相对量表示如图 6(b),可以看出使用Tikhonov正则化方法,在不同位置的误差均有所改善。位置误差在图像重建中十分关键,误差较大会造成重建不稳定,同时为后续的三维插值重构引入很大的物体形变。
|
图 6 位置误差仿真结果 |
通过上述评估手段及分析,可以得出选择合理的正规化参数,Tikhonov正则化方法对异物在大多数位置都呈现出更好评估结果,能够获得相对稳定可靠的电阻抗重建效果。
3 实验结果 3.1 实验平台在仿真分析的基础上,将算法应用到通过实验获得的数据组。如图 7(a),实验模型外壳为聚碳酸酯,形成一个开口向上的半径10 cm的半球,顶部有高度为2 cm的挡水。实验是由65个电极传感器阵列组成,采用单通道数据采集系统,电极放置如2.1所示,电极材料为Ag/AgCl,由于机械加工误差,直径为3.5~3.8 mm不等。

|
图 7 物理实验 |
外壳里装入电导率为0.1 S/m的琼脂作为背景物质,而在第2层和第3层水平电极阵列中央放置一个球形胡萝卜,直径约4 cm,电导率0.2 S/m(激励100 kHz)。在放入目标之前,笔者使用量筒测得其体积约为60 mL,如图 7(b)所示。电极被插入到水槽中,其后部被螺帽固定,侧面被粘合,并装水进行了密封性验证。电极阵列被集中到两组,屏蔽后接入电路板插座。由于在不同频率下胡萝卜的电导率特性不一,在此笔者取激励的频率为100 kHz,电流为5 mA以获得较高的分辨率[14]。
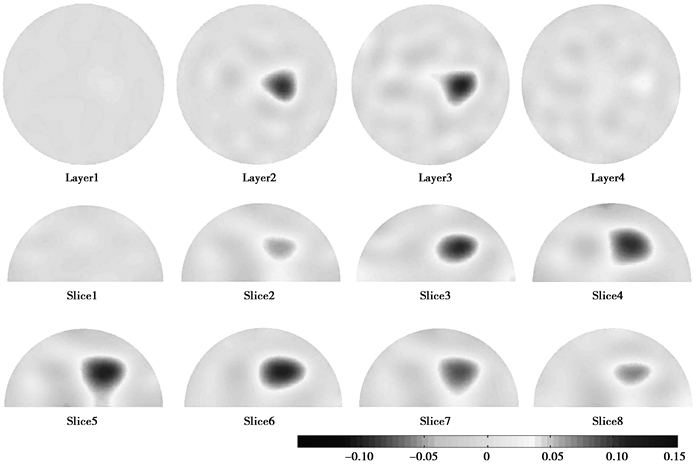
3.2 实验结果从图 8的结果可以看出,重建图像中电导率变化产生的扰动范围比实际物体所在位置更大,且形状不很规则,虽然在平面上的重建目标有轻微的形变,但电导率的变化还是能轻易地从周围的噪声中区分开。在图中的Layer4,存在一个伪像,在实验中物体实际上没有存在于该层,而只是穿过了Layer2和Layer3,而伪像大致出现在异物在该平面的投影位置,这可能是由于激励电流在模型顶部产生的边缘效应。
|
图 8 剖面图像重建 |
对于垂直剖面,从其电极阵列的分布可以看出,电极与水平面间存在一个夹角,且在靠近模型圆顶的位置该角度较大,该角度的存在会引入在水平剖面重建的误差,也成为以上水平剖面重建产生伪像的另一原因。而从垂直剖面重构图像可以看出物体被拉长成一个椭圆状,而实际异物是圆形。对于Tikhonov正则化算法二维图像重构与模拟结果基本符合,基于重建位于域内的单目标成像,能够得到较高的分辨率,位置误差在可接受的范围内[15]。
4 结论笔者提出了一种基于交叉平面数据进行三维电阻抗重构的方法,并通过仿真及实验对所提出的算法进行了验证,为后一阶段利用平面数据插值获得三维图像提供了有力基础。总体而言,电阻抗成像是一个非线性和病态的逆问题,这些因素使得图像重建难以获得可靠的、较高的图像分辨率。通过交叉平面的方式能够极大地改善成像效果,而重建结果与实际模型也能基本符合,且该方法计算量小,实现也相对简单,可适用于物体在空间上的定位及体积估计问题,为进一步研究提供了基础,并为实际应用提供了可能的途径。
| [1] | HOLDER D S. Electrical impedance tomography:methods, history and applications[M]. UK: Taylor & Francis, 2010. |
| [2] |
吴焕丽, 徐桂芝, 张帅, 等.
基于圆柱模型的三维电阻抗成像问题研究[J]. 山东大学学报:理学版, 2009, 44(5): 45–48.
WU Huanli, XU Guizhi, ZHANG Shuai, et al. Research of the three-dimensional electrical impedance tomography based on the cylinder model[J]. Journal of Shandong University:Natural Science, 2009, 44(5): 45–48. (in Chinese) |
| [3] | 刘国强. 医学电磁成像[M]. 北京: 科学出版社, 2006. |
| [4] |
陈民铀, 张晓菊, 罗辞勇, 等.
开放式电阻抗成像建模及其仿真[J]. 重庆大学学报, 2009, 32(7): 731–735.
CHEN Minyou, ZHANG Xiaoju, LUO Ciyong, et al. Modeling and simulation based on open electrical impedance tomography[J]. Journal of Chongqing University, 2009, 32(7): 731–735. DOI:10.11835/j.issn.1000-582X.2009.07.001 (in Chinese) |
| [5] | SADLEIR R J, ZHANG S U, TUCKER A S, et al. Imaging and quantification of anomaly volume using an eight-electrode 'hemiarray' EIT reconstruction method[J]. Physiological Measurement, 2008, 29(8): 913–927. DOI:10.1088/0967-3334/29/8/005 |
| [6] | STEPHENSON D R, MANN R, YORK T A. The sensitivity of reconstructed images and process engineering metrics to key choices in practical electrical impedance tomography[J]. Measurement Science and Technology, 2008, 19(9): 13–40. |
| [7] | CHENEY M, ISAACSON D, NEWELL J C, et al. NOSER:an algorithm for solving the inverse conductivity problem[J]. International Journal of Imaging Systems and Technology, 1990, 2(2): 66–75. DOI:10.1002/(ISSN)1098-1098 |
| [8] | LECHLEITER A, RIEDER A. Newton regularizations for impedance tomography:a numerical study[J]. Inverse Problems, 2006, 22(6): 1967–1987. DOI:10.1088/0266-5611/22/6/004 |
| [9] | GORODNITSKY I F, RAO B D. Sparse signal reconstruction from limited data using FOCUSS:A re-weighted minimum norm algorithm[J]. IEEE Transactions on Signal Processing, 1997, 45(3): 600–616. DOI:10.1109/78.558475 |
| [10] | CLAY M T, FERREE T C. Weighted regularization in electrical impedance tomography with applications to acute cerebral stroke[J]. IEEE Transactions on Medical Imaging, 2002, 21(6): 629–637. DOI:10.1109/TMI.2002.800572 |
| [11] | HANSEN P C, OLEARY D P. The use of the l-curve in the regularization of discrete Ⅲ-posed problems[J]. SIAM Journal on Scientific Computing, 1993, 14(6): 1487–1503. DOI:10.1137/0914086 |
| [12] | 徐振杰. 测量中不适定问题的正则化解法[M]. 北京: 科学出版社, 2006. |
| [13] | GRIEVE B D, MURPHY S, THOMPSON A B, et al. An accessible electrical impedance tomograph for 3D imaging[J]. Transactions of the Institute of Measurement and Control, 2010, 32(1): 31–50. DOI:10.1177/0142331208100108 |
| [14] | NAHVI M, HOYLE B S. Wideband electrical impedance tomography[J]. Measurement Science and Technology, 2008, 19(9): 11–40. |
| [15] | GRAHAM B M, ADLER A. Electrode placement con?gurations for 3D EIT[J]. Physiological Measurement, 2007, 28(7): 29. DOI:10.1088/0967-3334/28/7/S03 |
 2013, Vol. 36
2013, Vol. 36


