2. 重庆电力设计院, 重庆 400030
2. Electric Power Design Institute of Chongqing, Chongqing 400030, China
工程造价是电力线路建设工程中十分关键的一环,精确的工程造价估算,是实现电力线路工程经济性目标的重要手段。事实上,工程造价受多种因素影响,其构成复杂、情况多变、具有较大的模糊性,是一项多变量、非线性的复杂过程[1]。目前国内外的造价估算方法有:类比工程法[2]、回归分析法[3-4]、模糊数学法[5]等。以上方法均依赖于历史工程数据和工程审查者的工作经验,其主观性强,人为因素多,并消耗大量的人力资源,其客观性、准确性不够高[6]。
笔者正是在上述背景下提出了灰关联分析[7-8](grey relational analysis,GRA)与人工神经网络(artificial neural networks,ANN)相结合的工程造价估算方法(GRA-ANN法)。GRA的运用弥补了传统ANN法由于人为选取神经网络输入向量造成估算误差的缺陷,为神经网络输入向量的选取提供了理论依据。笔者通过GRA法筛选出影响工程造价的10个主要特征参数,作为神经网络输入向量;采用误差统计的方法,选取网络隐含节点数,以此构建GRA-ANN造价估算模型。以某市110 kV电力线路改造的工程造价为例,计算GRA-ANN网络估算模型静态投资的网络输出值与实际值之间的相对误差,评估造价估算精度并对比分析了LM-BP算法和传统BP算法训练GRA-ANN网络模型的误差变化情况。结果显示,GRA-ANN法对电力线路工程造价的估算和审查是准确的、有效的,是对造价估算方式的又一新的尝试。
1 方法理论 1.1 灰色关联分析灰色关联分析法是一种多因素统计分析方法,它用灰色关联度描述各因素间的关联程度,并以此区分影响事物的主要因素和次要因素;灰关联分析法所需数据少、运算简便,适合于对复杂系统的分析[9]。其基本分析流程如下。
1) 确定对比矩阵。
对原始数据进行分析处理,将因变量序列设定为参考序列X′0,将自变量序列设定为比较序列X′i(i=0,1,…,n),这n+1个序列构成了m×(n+1) 对比矩阵
| $ \begin{array}{*{20}{c}} {\left( {{{X'}_0},{{X'}_1}, \cdots ,{{X'}_n}} \right) = }\\ {{{\left( {\begin{array}{*{20}{c}} {{{X'}_0}\left( 1 \right)}&{{{X'}_1}\left( 1 \right)}& \cdots &{{{X'}_n}\left( 1 \right)}\\ {{{X'}_0}\left( 2 \right)}&{{{X'}_1}\left( 2 \right)}& \cdots &{{{X'}_n}\left( 2 \right)}\\ \vdots&\vdots&\vdots&\vdots \\ {{{X'}_0}\left( m \right)}&{{{X'}_1}\left( m \right)}& \cdots &{{{X'}_n}\left( m \right)} \end{array}} \right)}_{m \times \left( {n + 1} \right)}}。} \end{array} $ | (1) |
2) 数据标准化处理。
为了能对多组不同量纲的数据进行比较分析,保证各组数据具有等效性和同序性,需要对式(1) 中的数据进行标准化处理。笔者采用“初值法”的处理方法,如式(2) 所示。
| $ \begin{array}{*{20}{c}} {{x_i}\left( k \right) = \frac{{{{x'}_i}\left( k \right)}}{{\frac{1}{m}\sum\limits_{k = 1}^m {{{x'}_i}\left( k \right)} }},}\\ {i = 0,1, \cdots ,n;k = 0,1, \cdots ,m。} \end{array} $ | (2) |
3) 确定关联系数。
关联系数ξ0i(k)反映了比较序列X′i与参考序列X′0在K时刻的关联程度,取值满足0 < ξ0i(k)≤1的条件。其计算公式为
| $ \begin{array}{*{20}{c}} {{\xi _{0i\left( k \right)}} = \left( {\mathop {\min }\limits_i \mathop {\min }\limits_k \left| {{x_{0\left( k \right)}} - {x_{i\left( k \right)}}} \right| + } \right.}\\ {\left. {\rho \mathop {\max }\limits_i \mathop {\max }\limits_k \left| {{x_{0\left( k \right)}} - {x_{i\left( k \right)}}} \right|} \right)/\left( {\left| {{x_{0\left( k \right)}} - {x_{i\left( k \right)}}} \right| + } \right.}\\ {\left. {\rho \mathop {\max }\limits_i \mathop {\max }\limits_k \left| {{x_{0\left( k \right)}} - {x_{i\left( k \right)}}} \right|} \right),} \end{array} $ | (3) |
式中ρ为分辨系数,ρ∈(0,1),一般情况下取0.5,ρ越小表示越能提高关联系数间的差异。
4) 确定关联度。
计算关联度通常选用均值法和加权平均法两种,这里采用均值法,见式(4)。
| $ \begin{array}{l} {r_{0i}} = \frac{1}{m}\sum\limits_{k = 1}^m {{\xi _{0i}}\left( k \right)} = \\ \;\;\;\;\;\;\;\frac{1}{m}\left[ {{\xi _{0i}}\left( 1 \right) + {\xi _{0i}}\left( 2 \right) + \cdots + {\xi _{0i}}\left( m \right)} \right]。\end{array} $ | (4) |
5) 依关联度排序。
关联度r0i越大,表示比较序列X′i与参考序列X′0变化的态势越趋于一致,说明X′i对X′0的影响程度也就越大[10]。为了减少目标之间的错误关联,可以确定一个阈值r,当r < r0i时,视为目标关联;当r>r0i时,则视为虚假目标。r的取值可根据分辨率ρ的大小等因素确定。
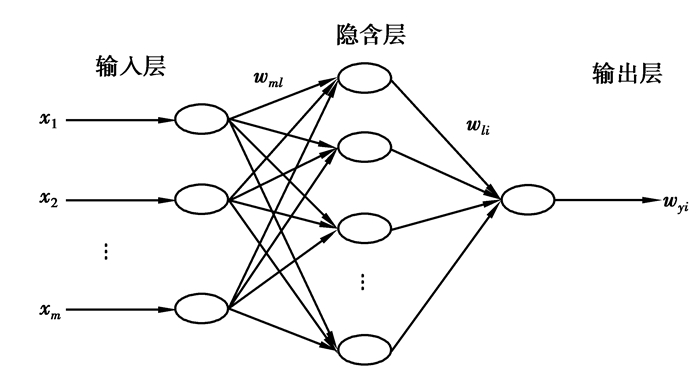
1.2 BP网络方法BP网络是一种多层前馈型神经网络,具有较强的函数逼近能力和自适应学习能力,是人工神经网络中应用最广泛的网络形式[11-12]。如图 1所示,BP网络有m个输入,1个输出,wml为输入层的第m个神经元到隐含层第l个神经元间的权值,wlj为隐含层第l个神经元到输出层第i个神经元间的连接权值。xm为神经网络的输入,yi为其输出。
|
图 1 BP神经网络结构 |
以工程特征参数作为输入,具体工程造价作为输出,建立BP神经网络工程造价估算模型。其思路是:首先确定神经网络拓扑结构,建立灰关联神经网络模型,最后给出LM算法的实施步骤。
2.1 网络拓扑结构的确定 2.1.1 基于灰关联法的神经网络输入向量的提取笔者将工程特征参数作为神经网络的输入。工程特征参数是指能够体现工程特点,且能反映工程主要成本构成的重要因素。影响电力线路改造工程造价的因素较多,且影响程度不同,如何正确地选取影响因素是决定模型估算准确性的关键。
在分析电力线路改造工程造价影响因素的基础上,笔者提取了15种关键的工程特征参数,利用灰关联分析法(公式(1)~(4))分别计算出参数与样本值的关联度,结果如表 1所示(关联度按从大到小顺序排列)。将关联度大于100的10个工程特征参数选为神经网络的输入向量,即:线路截面、线路回路数、线路全长、丘陵系数、跨越公路次数、跨越高压线次数、跨越弱电线路、跨越其他次数、导线单价和塔材单价。
| 表 1 各工程特征信息的关联度 |
其中,同一地区一般属同种气象条件区,不考虑气象条件对工程造价的影响,不作为神经网络的输入向量;线路清理费用占整个线路改造工程造价中很小的一部分,并且走廊清理费用由于人为因素影响太大,会影响整个估算系统的稳定,因此线路走廊清理费用不作为神经网络输入向量。
2.1.2 神经网络的输出、隐含层确定输出向量:将静态投资作为神经网络输出。计算静态投资网络输出值与实际值之间的相对误差,以审核工程造价估算精度。
隐含层:隐含层节点数的选取决定着BP网络的收敛速度。根据Kolmogorov定理[13]选择隐含层节点数为21时,发现GRA-ANN网络收敛速度非常慢。在这种情况下,笔者统计了不同隐含层节点数l对应的GRA-ANN网络的平均误差值E,结果见表 2。由表 2可知,网络收敛效果最好的隐含层节点数在7~10之间,因此选择隐含层节点数为8。
| 表 2 不同l的BP网络平均误差E |
笔者采用levenberg-marquardt (LM) [14-16]算法训练GRA-ANN网络。设di为神经网络的第i个期望输出,权值向量w表示为
| $ {\mathit{\boldsymbol{w}}^{\rm{T}}} = \left[ {{w_{11}},{w_{12}}, \cdots ,{w_{ml}}, \cdots ,{w_{li}}} \right], $ | (5) |
则可以定义误差指标函数
| $ E\left( w \right) = \frac{1}{2}\sum\limits_{i = 1}^N {{{\left( {{d_i} - {y_i}\left( w \right)} \right)}^2}} = \frac{1}{2}\sum\limits_{i = 1}^N {{e_i}{{\left( w \right)}^2}} 。$ | (6) |
E(w)的梯度为
| $ \nabla E\left( w \right) = \sum\limits_{i = 1}^N {{e_i}\left( w \right)\frac{{{\partial _{ei}}\left( w \right)}}{{\partial w}}} = {\mathit{\boldsymbol{J}}^{\rm{T}}}\left( w \right)e\left( w \right), $ | (7) |
式中:
| $ \mathit{\boldsymbol{J}}\left( w \right) = \left[ {\begin{array}{*{20}{c}} {\frac{{{\partial _{e1\left( w \right)}}}}{{{w_{11}}}}}&{\frac{{{\partial _{e1\left( w \right)}}}}{{{w_{12}}}}}& \cdots &{\frac{{{\partial _{e1\left( w \right)}}}}{{{w_{ml}}}}}& \cdots \\ {\frac{{{\partial _{e2\left( w \right)}}}}{{{w_{11}}}}}&{\frac{{{\partial _{e2\left( w \right)}}}}{{{w_{12}}}}}& \cdots &{\frac{{{\partial _{e2\left( w \right)}}}}{{{w_{ml}}}}}& \cdots \\ \vdots&\vdots&\vdots&\vdots&\vdots \\ {\frac{{{\partial _{eN\left( w \right)}}}}{{{w_{11}}}}}&{\frac{{{\partial _{eN\left( w \right)}}}}{{{w_{12}}}}}& \cdots &{\frac{{{\partial _{eN\left( w \right)}}}}{{{w_{ml}}}}}& \cdots \end{array}} \right], $ | (8) |
J为雅可比矩阵,其元素为网络误差对权值和阈值的一阶导数。设网络的误差向量eT= [e1,e2,…,eN],则有
| $ \begin{array}{l} \nabla {E^2}\left( w \right) = \frac{{\partial \sum\limits_{i = 1}^N {{e_{i\left( w \right)}}\frac{{{\partial _{ei\left( w \right)}}}}{{\partial w}}} }}{{\partial w}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^N {\left[ {\frac{{{\partial _{ei\left( w \right)}}}}{{\partial w}} \cdot \frac{{{\partial _{ei\left( w \right)}}}}{{\partial w}} + {e_{i\left( w \right)}}\frac{{{\partial ^2}{e_{i\left( w \right)}}}}{{\partial {w^2}}}} \right]} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{J}}\left( w \right){\mathit{\boldsymbol{J}}^{\rm{T}}}\left( w \right) + \sum\limits_{i = 1}^N {{e_{i\left( w \right)}}\frac{{{\partial ^2}{e_{i\left( w \right)}}}}{{\partial {w^2}}}} 。\end{array} $ | (9) |
当误差指标函数逼近最小值时,式(9) 中
| $ \begin{array}{l} {w_{t + 1}} = {w_t} + \Delta {w_t} = \\ \;\;\;\;\;\;\;\;\;{w_t} - \left[ {{\mathit{\boldsymbol{J}}^{\rm{T}}}\left( {{w_t}} \right)\mathit{\boldsymbol{J}}\left( {{w_t}} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;{\left. {{\mu _t}\mathit{\boldsymbol{I}}} \right]^{ - 1}}.{\mathit{\boldsymbol{J}}^{\rm{T}}}\left( {{w_t}} \right)e\left( {{w_t}} \right), \end{array} $ | (10) |
式中:wt为t时刻的权值;I为单位矩阵。在迭代过程中,如果训练成功,就减小μ值;如果训练失败,就增加μ值,μ值的改变通过在程序中设置μ的初始值、减小率、增长率及最大值实现,最终达到降低误差指标函数E(w)的目的。
3 实例分析为了验证模型的可靠性和计算精度,选择某市已改造的100条110 kV的电力线路工程造价进行分析。选取其中90条线路作为学习样本,剩余10条线路作为网络的测试样本,进行数据采集。笔者采用LM算法训练GRA-ANN网络,对测试样本进行相对误差估算,估算误差见表 3;表 4是电力线路改造工程造价模型的输入与对应的输出属性表,其中10个输入属性的提取见2.1.1节,静态投资为输出属性(表 4仅列出其中15条线路输入、输出值)。
| 表 3 静态投资实际值与预测值估算误差表 |
| 表 4 电力线路改造工程造价输入、输出属性表 |
按照相对误差计算式可得静态投资的估算误差表(相对误差)。
| $ 相对误差 = \left| {\frac{{输出值 - 实际值}}{{实际值}}} \right| \times 100\% 。$ | (11) |
表 3是采用LM算法所得GRA-ANN网络的10条测试样本的实际值和预测值的估算误差,由表 3可知,经过训练后的灰关联神经网络对于电力线路改造工程的静态投资估算已经达到相当高的精度。其中,静态投资网络输出值与实际值之间的相对误差最大为3.72%,最小仅为1.85%。输出结果说明灰关联神经网络估算精度高,运用GRA-ANN法对于电力线路改造工程造价的快速估算效果良好。
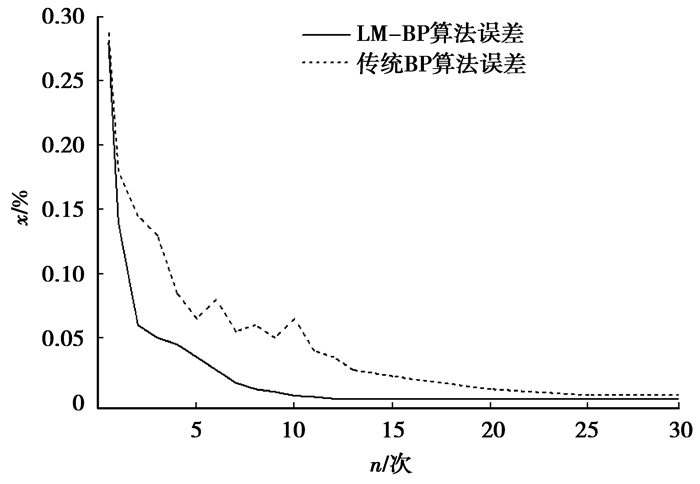
保持网络结构不变,采用传统的BP算法对GRA-ANN进行训练,与采用的LM-BP算法进行比较,所得网络的误差变化曲线如图 2所示(图中X表示均方误差,N表示训练次数)。LM-BP与传统BP算法的网络性能参数见表 5,由表 5可知,LM-BP算法的网络性能更好,收敛速度更快,逼近能力更强。
|
图 2 误差下降曲线 |
| 表 5 BP与LM-BP的网络性能比较 |
图 2是训练样本经过90次训练后,总误差的下降曲线。从图 2中可以看出采用的LM-BP网络误差下降速度快,整体误差比传统的BP网络模型的整体误差更低。因此采用LM-BP算法训练GRA-ANN网络效果良好。
上述方法可以应用到电力线路工程造价估算和审查中。在建立新的送电线路工程造价估算系统时,要注意数据的搜集和整理,力求在多变量多样本的数据下建立估算模型。
4 结语1) 采用灰关联分析法对各工程特征参数进行灰关联度计算并排序,确定神经网络的输入向量,构建GRA-ANN造价估算模型。结果显示静态投资的相对误差最大为3.72%,最小为1.85%,说明10个工程特征参数的选取可以较好地表征工程造价,降低了估算误差。实验证明,GRA-ANN法对电力线路改造工程造价的估算和审查是准确的、有效的。
2) 采用LM-BP算法对GRA-ANN网络进行训练,结果表明LM-BP算法误差下降速度较传统BP算法更快,而且整体误差更低。
| [1] |
李泓泽, 郎斌.
全寿命周期造价管理在电力工程造价管理中的应用研究[J]. 华北电力大学学报:社会科学版, 2008, 25(1): 7–11.
LI Hongze, LANG Bin. The application of the whole life cycle engineering cost management on the electricity engineering field[J]. Journal of North China Electric Power University:Social Sciences, 2008, 25(1): 7–11. (in Chinese) |
| [2] | ANGELIS L, STAMELOS I, MORISIO M.Building a software cost estimation model based on categorical data[C]//Proceedings of 2001 the 7th International Software Metrics Symposium, April, 04-06, 2001, London, UK.Piscataway:IEEE Press, 2001:4-15. http://ieeexplore.ieee.org/document/965340/ |
| [3] |
宿莎莎, 汪飞星, 王彩凤.
改进的标准模糊神经网络的工程造价快速估算[J]. 系统仿真学报, 2008, 20(5): 1151–1154.
SU Shasha, WANG Feixing, WANG Caifeng. Fuzzy neural network based on improved standard model and its application in calculating project's cost quickly[J]. Journal of System Simulation, 2008, 20(5): 1151–1154. (in Chinese) |
| [4] | ASHWORTH A. Accuracy in estimating[J]. Chartered Quantity Surveyor, 1982(4): 191–194. |
| [5] |
牛培峰, 高龙, 孟凡东, 等.
基于神经网解耦的循环流化床锅炉燃烧系统自适应模糊控制[J]. 仪器仪表学报, 2011, 32(5): 1021–1025.
NIU Peifeng, GAO Long, MENG Fandong, et al. Adaptive fuzzy control based on neural network decoupling for circulating fluidized bed boiler combustion system[J]. Chinese Journal of Scientific Instrument, 2011, 32(5): 1021–1025. (in Chinese) |
| [6] |
辛立民, 杨芸.
基于神经网络的建筑工程投标报价预测[J]. 安徽工程科技学院学报:自然科学版, 2008, 23(4): 44–47.
XIN Limin, YANG Yun. Approach of constructional engineering bidding forecasting based on neural networks[J]. Journal of Anhui University of Technology and Science:Natural Science, 2008, 23(4): 44–47. (in Chinese) |
| [7] | LIN Y H, LEE P C, CHANG T P. Practical expert diagnosis model based on the grey relational analysis technique[J]. Expert Systems with Applications, 2009, 36(2): 1523–1528. DOI:10.1016/j.eswa.2007.11.046 |
| [8] | LIN Y H, LEE P C, CHANG T P, et al. Practical expert diagnosis model based on the grey relational analysis technique[J]. Expert Systems with Applications, 2011, 36(6): 7302–7306. |
| [9] |
黄新波, 罗兵, 王勇, 等.
用灰关联法分析气象因素对MOA在线监测的影响[J]. 高电压技术, 2010, 36(6): 1468–1474.
HUANG Xinbo, LUO Bing, WANG Yong, et al. Influence of climatic factors on on-line monitoring of MOA using grey relational analysis[J]. High Voltage Engineering, 2010, 36(6): 1468–1474. (in Chinese) |
| [10] |
黄捍东, 赵迪, 张如伟, 等.
基于灰关联和遗传算法的地震属性优化方法[J]. 石油地球物理勘探, 2010, 45(3): 381–383.
HUANG Handong, ZHAO Di, ZHANG Ruwei, et al. Seismic attribute optimization method based on grey relational analysis and genetic algorithm[J]. Oil Geophysical Prospecting, 2010, 45(3): 381–383. (in Chinese) |
| [11] | DING S F, XU L, SU C Y, et al. An optimizing method of RBF neural network based on genetic algorithm[J]. Neural Computing and Applications, 2012, 21(2): 333–336. DOI:10.1007/s00521-011-0702-7 |
| [12] | MANIK P D, VIVEK S S. Predicting effective viscosity of magnetite ore slurries by using artificial neural network[J]. Powder Technology, 2012, 219: 264–270. DOI:10.1016/j.powtec.2011.12.058 |
| [13] |
周建华, 胡敏强.
自构形神经网络在变压器故障诊断中的应用[J]. 电工技术学报, 2004, 19(9): 77–81.
ZHOU Jianhua, HU Minqiang. Application of auto-structural neural network in diagnosing transformer faults[J]. Transactions of China Electrotechnical Society, 2004, 19(9): 77–81. (in Chinese) |
| [14] | PENG Y, ZHOU H C. Fuzzy optimization neural network model based on LM algorithm[J]. Journal of Harbin Institute of Technology, 2010, 17(3): 431–436. |
| [15] |
王建梅, 覃文忠.
基于L-M算法的BP神经网络分类器[J]. 武汉大学学报, 2005, 30(10): 237–240.
WANG Jianmei, QIN Wenzhong. BP neural network classifier based on Levenberg-Marquardt algorithm[J]. Journal of Wuhan University, 2005, 30(10): 237–240. (in Chinese) |
| [16] |
李永明, 王玉斌, 王颖, 等.
数据挖掘和神经网络技术的电力工程造价应用[J]. 重庆大学学学报:自然科学版, 2008, 31(6): 663–666.
LI Yongming, WANG Yubin, WANG Ying, et al. Application of project cost forecasting with data mining and neural network technologies for power engineering[J]. Journal of Chongqing University:Natural Science Edition, 2008, 31(6): 663–666. (in Chinese) |
| [17] | 哈姆, 科斯塔尼克. 神经计算原理[M]. 叶世伟, 王海娟, 译. 北京: 机械工业出版社, 2007. |
 2013, Vol. 36
2013, Vol. 36

