1b. 北京科技大学 计算机与通信工程学院, 北京 100083;
2. 昆明理工大学 冶金与能源工程学院, 昆明 650093
1b. School of Computer and Communication Engineering, University of Science and Technology Beijing, Beijing 100083, China;
2. Faculty of Metallurgical and Energy Engineering, Kunming University of Science and Technology, Kunming 650093, China
钢包周转数量控制水平是反映炼钢厂生产组织能力的一项重要指标。合理控制钢包周转数量对减少包衬和钢水温降、实现节能降耗及保持连铸机恒拉速浇注都有重要意义。因此,在保证生产连续有序运行前提下,尽量减少钢包周转数量历来是炼钢厂关心的重要问题。
当前炼钢-连铸生产计划主要针对转炉、精炼和连铸等工序,围绕生产计划制定[1]与调度优化展开研究[2-3],而作为炼钢流程控制关键环节的钢包,在生产计划编制中通常不予考虑。这方面仅在涉及钢包周转的生产计划优化中[4],采用EM-Plant仿真方法进行研究,但未能就生产计划对钢包周转数量的影响深入讨论。而笔者研究发现生产计划编排对钢包周转数量计算却有着重要影响,需将钢包周转数量研究提升到生产计划层面上进行考虑。
已有钢包周转数量计算的研究提出了产量计算法、时间计算法、周转期匹配法和钢包分类法等[5-8],根据一天或一个班次的产量,针对一座转炉或一台铸机计算钢包周转数量,然后将几座转炉或几台铸机的计算结果求和,但现有方法没有考虑不同浇次间的钢包互用对钢包周转数量的影响,使计算的钢包周转数量存在偏差,特别是多浇次同时生产时钢包周转数量会产生数量叠加现象,计算结果往往大于实际钢包周转数量,难于准确表达多浇次同时生产时的钢包周转数量情况。
笔者针对已有研究的局限,提出基于浇次计划的钢包周转数量计算模型和优化方法。以Q炼钢厂钢包为研究对象,通过甘特图[9-10]对钢包周转数量与浇次计划的关系进行研究,分析了浇次计划对钢包周转数量的影响,在此基础上,提出基于浇次计划的钢包周转数量计算模型,采用EM-Plant[11-12]仿真方法,输入实际生产数据验证了模型的准确性。并且针对热修时间波动对钢包周转数量的影响,调整浇次计划对钢包周转数量进行了优化。研究成果对炼钢厂钢包周转组织与浇次计划编排之间的相互配合,实现流程生产组织优化具有重要指导意义。
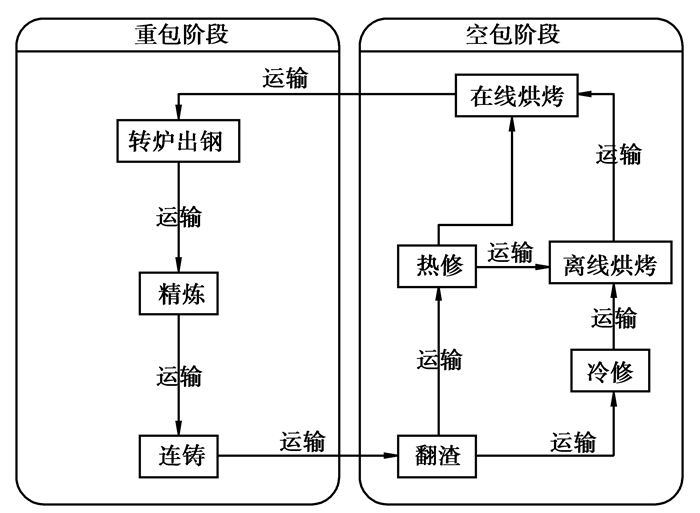
1 钢包周转过程解析 1.1 钢包周转过程现场调研Q炼钢厂现有2座210t转炉,2座双工位RH,1座双工位LF,2座CAS精炼,2台双流板坯连铸机,3个热修工位,6个离线烘烤位和2个在线烘烤位,其钢包公称容量为210t,构成了典型炼钢-精炼-连铸相结合的转炉炼钢生产模式。钢包周转具体过程如图 1所示。
|
图 1 钢包周转过程 |
钢包在转炉-连铸区段周转主要经历过程为:在线烘烤、转炉出钢、精炼、连铸、翻渣、热修等。可以根据盛载钢水情况,将钢包周转过程划分为:重包和空包两个阶段。重包阶段主要包括:转炉出钢、精炼和连铸等;空包阶段一般要经历:翻渣、热修和在线烘烤等环节。
1.2 钢包周转过程时间解析在钢包周转过程现场调研基础上,通过统计Q炼钢厂6500炉钢包周转历史数据,对钢包周转时间进行解析研究,得出钢包在重包和空包阶段的工序(指转炉、连铸)处理和工序间运输时间的最大、最小和平均值,如表 1所示。
| 表 1 钢包周转时间min |
为实现钢包周转数量较为准确地计算,需在生产计划层面上,考虑浇次计划对钢包周转数量的影响,提出合理的钢包周转数量计算模型。鉴于甘特图作为解决车间生产排序问题的有效工具,能清楚地表现出生产计划与各工序间的关系。因此,笔者采用甘特图对炼钢浇次计划与钢包周转数量的关系进行研究,在此基础上,提出基于浇次计划的钢包周转数量计算模型。
2.1 单浇次钢包周转数量计算实际生产中,为了减少钢包周转过程中的包衬温降,钢包周转一般采用钢包先到先用的周转原则。具体为:烘烤出钢开始前若钢包完成热修,则该钢包由前面炉次转到后面炉次继续使用;若钢包未完成热修,则需添加使用新钢包周转。
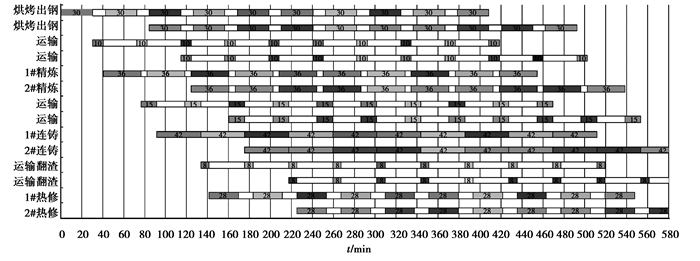
通常情况下炼钢厂一个浇次的连浇炉数为8~12炉,以10炉连浇为例,结合钢包周转原则绘制钢包周转甘特图,描述单浇次的钢包周转和使用情况,如图 2所示。

|
图 2 单浇次钢包周转甘特图 |
本浇次同一钢包用相同颜色表示,一共出现了5个颜色的不同钢包。由于浇次的第5炉烘烤出钢要求钢包在第168 min前投入使用,而第1炉使用的1号钢包在第169.6 min才完成热修,因此,根据钢包周转原则本浇次第5炉还需添加1个新钢包,而第6炉的烘烤出钢开始时间在第210 min,可继续使用1号钢包,所以单浇次共使用了5个钢包。
此外,由图 2可知,钢包周转一次(从一次烘烤出钢到完成热修)所用时间,其表达式为
| $ {t_{{\rm{zz}}}} = {t_{\rm{z}}} + {t_{\rm{k}}}。$ | (1) |
通过钢包周转甘特图对单浇次钢包周转过程规律的研究发现,钢包周转数量与连铸大包浇注时间和钢包周转时间有关,可用钢包周转时间与大包浇注时间来计算单浇次钢包周转数量,如下式:
| $ n = \left[ {\frac{{{t_{{\rm{zz}}}}}}{{\bar t}}} \right], $ | (2) |
式中:tzz为钢包周转时间,min;tz为重包阶段时间,min;tk为空包阶段时间,min;n为钢包周转数量,个;t为大包浇铸时间,min。
2.2 多浇次钢包周转数量计算以上为1台连铸机生产时,单浇次钢包周转数量计算公式,通过对现场钢包周转使用过程的研究发现:若是2台连铸机的2个浇次同时生产(实际生产多数情况如此),钢包周转数量计算并不仅是简单一台连铸机钢包周转数量计算后求和。而是多数情况下会发生2台铸机同时浇铸时浇次间钢包互用的现象,一台铸机的浇次后几炉使用过的钢包转到另一台铸机的浇次中继续周转,这样如果简单按照一台连铸机的一个浇次计算钢包周转数量后求和,会造成钢包周转数量的计算叠加,结果往往大于实际钢包周转数量。由此,针对浇次间重合炉数对钢包周转数量的影响进行研究。浇次间重合炉数是指:不同浇次同时浇铸时,重合浇铸的炉次数量。分别列出重合8炉和重合3炉的钢包周转甘特图,如图 3和图 4所示。
|
图 3 重合8炉 |

|
图 4 重合3炉 |
由图 3可知,1号铸机连浇第1炉使用的1号钢包在该浇次第6炉烘烤出钢开始前完成热修,这样第6炉可再循环使用该浇次的1号钢包,以此类推,1号铸机的浇次钢包周转数量为5个。2号铸机的钢包周转情况与1号铸机相同,钢包周转数量也为5个,因此两台铸机一共使用了10个钢包。而当浇次间重合3炉时,钢包周转数量却发生了变化,如图 4所示。
1号铸机的浇次钢包周转数量为5个,按照钢包周转原则规定,2号铸机的浇次前3炉需添加3个新钢包,到第4炉时1号铸机第6炉的钢包才转到2号铸机的浇次中继续使用,这样2个浇次一共使用8个钢包。由此可知,如果按照计算单浇次钢包周转数量后求和的方式,计算浇次间钢包周转数量就会比实际需要多2个,从而造成计算上的偏差。
从图 3和图 4的钢包周转数量比较可看出,浇次计划中重合炉数的差异,会导致浇次衔接时钢包周转数量的变化,从而使不同方法计算的钢包周转数量差别很大。研究发现:1号铸机的钢包会适时转到2号铸机的浇次中继续使用,钢包周转过程中存在浇次间的钢包互用现象,而不是两台铸机的钢包周转互不影响,只在其各自的浇次内周转。
通过浇次计划与钢包周转数量关系的解析研究,得出浇次间钢包周转数量的变化规律,多浇次的钢包周转数量不仅与连铸大包浇注时间和钢包周转时间有关,还与浇次间重合炉数有重要关联,因此,需结合钢包周转时间和大包浇注时间以及浇次间重合炉数三者来共同计算多浇次的钢包周转数量,由此提出不同重合炉数情况下的钢包周转数量计算模型。
1) 当2台连铸机浇次间重合炉数m大于单浇次钢包周转数量n时,即m>n时,结合图 3,提出此情况下的浇次间钢包周转数量计算公式为
| $ {n_{\rm{z}}} = \left[ {\frac{{{t_{{\rm{zz,}}{i}}}}}{{\overline {{t_i}} }}} \right] + \left[ {\frac{{{t_{{\rm{zz,}}{i + 1}}}}}{{\overline {{t_{i + 1}}} }}} \right]。$ | (3) |
2) 当2台连铸机浇次间重合炉数m小于单浇次钢包周转数量n时,即m≤n时,结合图 4,提出此情况下的浇次间钢包周转数量计算公式为
| $ {n_{\rm{z}}} = \left[ {\frac{{{t_{{\rm{zz,}}{i}}}}}{{\overline {{t_i}} }}} \right] + \left[ {\frac{{{t_{{\rm{zz,}}{i + 1}}}}}{{\overline {{t_{i + 1}}} }}} \right] + m, $ | (4) |
式中:nz为钢包周转总数,个;tzz,i为第i个浇次的钢包周转时间,min;ti为第i个浇次的大包浇铸时间,min;tzz,i+1为第i+1个浇次的钢包周转时间,min;ti+1为第i+1个浇次的大包浇铸时间,min;m为重合炉数。
以上为常见的2台铸机生产模式炼钢厂钢包周转数量的计算,而实际中3台铸机生产模式的炼钢厂也较为普遍,需进一步针对3台铸机生产模式炼钢厂的钢包周转数量进行计算。
实际生产中,由于转炉、精炼和连铸三者间生产节奏要求和连铸更换中间包等操作影响,3台铸机生产模式的炼钢厂多采用3台铸机交替生产的方式,多数情况下只有1台或2台铸机浇铸运行,因此也适用公式(3) 或(4)。而炼钢产量增加、生产节奏加快时,需3台铸机同时生产,此时钢包周转数量达到最大值,提出计算公式为
| $ {n_{\rm{z}}} = {\left[{\frac{{{t_{{\rm{zz}}}}}}{{\bar t}}} \right]_{\max }} + {m_{i, i + 1}} + {m_{i, i + 2}}, $ | (5) |
式中:mi,i+1为第i和第i+1个浇次间重合炉数;mi,i+2为第i和第i+2个浇次间重合炉数。
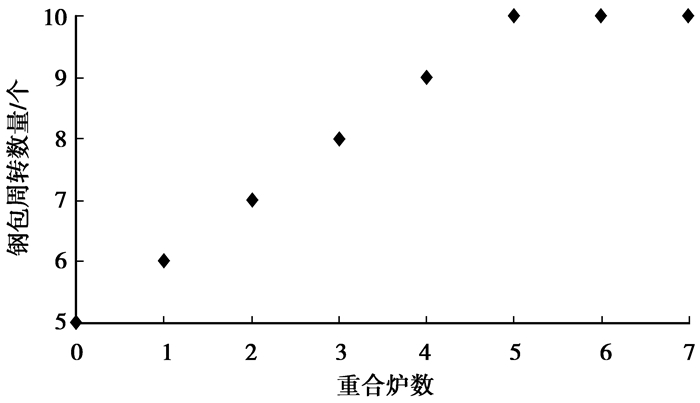
根据钢包周转甘特图,对2台铸机生产模式下重合炉数与钢包周转数量的关系进行描述,如图 5所示。
|
图 5 重合炉数与钢包周转数量关系 |
钢包周转数量随重合炉数增加而增加,但浇次间重合炉数超过5炉,大于单浇次钢包周转数量时,浇次间钢包周转数量达到最大值,此后一直为10个,不再随重合炉数增加而改变。由此,生产调度专家在为炼钢生产准备钢包时,只需根据浇次计划计算出当天所需钢包周转数量的最大值,就能比较准确掌握全天的钢包周转数量情况,保证浇次计划顺利进行。
3 仿真验证为验证计算模型的准确性,笔者采用流程仿真软件建立钢包周转仿真模型,对计算模型进行验证,仿真模型包括仿真建模和模型验证两部分。
3.1 仿真建模仿真模型中,钢包采用Container建模,钢水用Entity建模,双工位RH和双工位LF采用ParallelProc建模,CAS工位采用SingleProc建模,运输线用Line建模,TableFile用于储存生产计划,钢水由Source输入,过转炉后由Drain回收。用Simtalk语言编写钢包周转的控制语言,使钢包在特定的生产计划下周转,得出钢包周转数量结果。
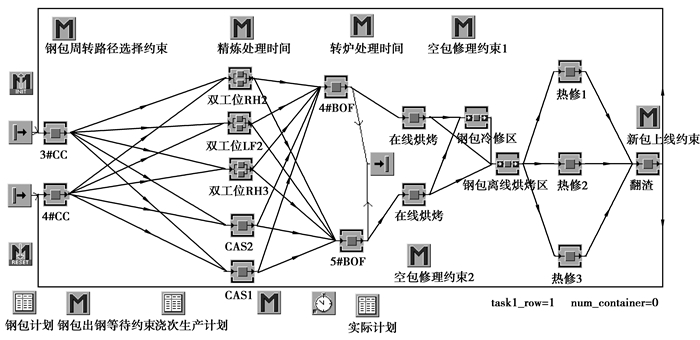
模型考虑钢包实际周转过程中的时间波动,参照表 1钢包周转时间的最大值、最小值和平均值设置钢包的工序处理时间和工位间运输时间。根据该炼钢厂实际生产配置,建立仿真模型,如图 6所示。
|
图 6 钢包周转仿真 |
浇次计划:2012年6月至2012年12月,日产41、45和47炉的典型钢种浇次计划,如表 2所示。仿真验证结果,如表 3所示。
| 表 2 实际浇次计划 |
| 表 3 钢包周转数量 |
从钢包周转数量比较来看,多数情况下,仿真数量都比计算数量结果多一个,是因为计算模型求解过程忽略了钢包周转的时间波动,主要是空包阶段的热修时间波动。对于热修时间过长的钢包,现场调度往往会采用达到上线温度要求的烘烤钢包来替换。为此,现场会结合钢包热修时间等情况,多备1~2个钢包以保证生产连续,而仿真模型正是考虑热修时间的波动并解决了这一问题,结果比较接近实际,因此可以说,计算模型能够较准确地反应实际的钢包周转数量,对现场生产具有一定指导意义。
4 基于浇次计划的钢包周转数量优化 4.1 热修时间对钢包周转数量的影响钢包重包阶段由于钢种的工艺和温度制度要求,使钢包的处理和运输时间受到严格限制,因此时间波动不大;但作为决定钢包上线的空包阶段,由于缺少操作制度要求时间波动较大,特别是钢包热修时间,现场经验表明热修时间的波动对钢包周转数量的影响很大,如图 7所示。

|
图 7 热修时间波动 |
根据钢包周转原则,1号铸机的浇次最后一个炉次烘烤出钢开始时间为378 min,但由于浇次第5炉用过的钢包热修时间过长,在第379 min完成修理,因此添加了1个新钢包;同时,2号铸机浇次的前3个炉次烘烤出钢开始前,因为1号铸机没有多余钢包供给2号铸机的浇次使用,所以也增加了3个新钢包,这样两个浇次一共使用9个钢包,比较图 4中正常热修时间(一般为28 min)下的钢包周转数量多1个。这是由于现场钢包热修缺少操作制度要求,造成钢包不同修理部位的时间波动大,如前面浇次的第5炉钢包热修时间达到68 min,使5号钢包未能及时完成修理转入后面炉次继续周转,因此,为保证铸机连续浇铸,该浇次最后一个炉次需再增加1个新钢包。然而钢包周转数量增加却带来许多问题,一方面增加了天车吊运钢包的频率,使生产调度更加复杂;另一方面也延长了其他钢包的空包散热时间,降低了红包出钢率,但为保证钢包的热状态水平,就需要转炉提高出钢温度补偿,增加了能源消耗。
4.2 钢包周转数量优化笔者在热修时间波动对钢包周转数量的影响基础上,进一步研究通过调整浇次计划对钢包周转数量优化,结果如图 8所示。
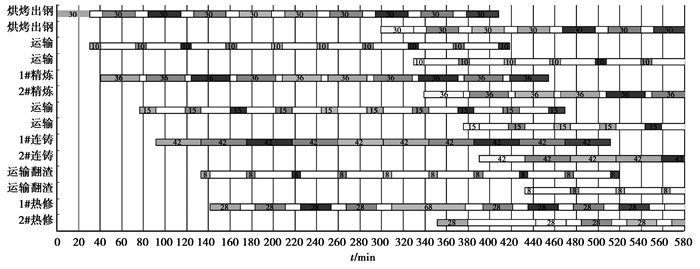
|
图 8 浇次计划优化 |
2号铸机浇次的开浇时间向后推迟了5 min,使该浇次第3炉在第384 min开始烘烤出钢操作,这样1号铸机浇次第5炉用过的钢包经热修后就能直接转到2号铸机浇次的第3炉继续使用,这样2号铸机的浇次减少了1个新钢包使用,最终两浇次钢包周转数量为8个,比图 7中钢包周转数量优化了1个。研究得出浇次开浇时间的适当调整可有效减少钢包周转数量,优化浇次开浇时间可为钢包热修提供灵活的时间空间,特别可以起到优化钢包周转数量的作用。因此,如果钢包热修时间较长,炼钢厂现场调度可根据浇次计划和钢包周转数量,在保证产量前提下对后面浇次开浇时间适当调整,优化钢包周转数量。将调整后的浇次计划代入钢包周转仿真模型进行验证,得出钢包周转数量结果,如表 4所示。
| 表 4 钢包周转数量优化 |
从仿真结果比较看,浇次计划调整后钢包周转数量减少1个,说明针对热修时间波动对钢包周转数量的影响,通过浇次计划的优化调整可解决这一问题,达到钢包周转数量优化的目的。由此,为优化钢包周转数量,建议Q炼钢厂应尽量避免前后浇次同时开浇,必要时可推迟后面浇次开浇时间,例如5~15 min。而同时,开浇时间推迟过多会降低连铸机的作业率,进而影响产量,也无必要。
5 结论1) 通过钢包周转甘特图对浇次计划与钢包周转数量关系进行研究,发现浇次间重合炉数对钢包周转数量计算有重要影响,在此基础上,提出基于浇次计划的钢包周转数量计算模型实用性较强,对指导现场准备钢包生产和控制钢包周转数量具有应用价值。
2) 浇次计划研究为优化钢包周转数量开拓了新思路,鉴于钢包热修时间对钢包周转数量影响,建议现场采取措施一方面将空包纳入生产计划考虑范围,规范空包处理时间,特别是热修操作时间;另一方面浇次计划编排时结合钢包周转数量情况,可适当调整浇次开浇时间,必要时可推迟。
| [1] |
何腊梅, 郑忠, 高小强, 等.
基于时间倒推和流程仿真炼钢生产计划的制定[J]. 重庆大学学报:自然科学版, 2006, 29(9): 60–63.
HE Lamei, ZHENG Zhong, GAO Xiaoqiang, et al. Production planning method for steelmaking-continuous casting process based on time backward and process simulation[J]. Journal of Chongqing University:Natural Science Edition, 2006, 29(9): 60–63. (in Chinese) |
| [2] | TANG L X, LIU J Y, RONG A Y, et al. A review of planning and scheduling systems and methods for integrated steel production[J]. European Journal of Operational Research, 2011, 133(1): 1–20. |
| [3] |
郑忠, 刘海玉, 高小强.
炼钢-连铸生产计划调度一体化的仿真优化模型[J]. 重庆大学学报, 2010, 33(3): 108–113.
ZHENG Zhong, LIU Haiyu, GAO Xiaoqiang, et al. Optimal model on integrated production planning and scheduling of steelmaking and continuous casting process[J]. Journal of Chongqing University:Natural Science Edition, 2010, 33(3): 108–113. DOI:10.11835/j.issn.1000-582X.2010.03.020 (in Chinese) |
| [4] | 张涛. 涉及钢包周转的炼钢-连铸生产作业计划优化方法研究[D]. 重庆: 重庆大学, 2009. |
| [5] |
刘青, 赵平, 吴晓东, 等.
钢包的运行控制[J]. 北京科技大学学报, 2005, 27(2): 235–239.
LIU Qing, ZHAO Ping, WU Xiaodong, et al. Control stralegy for ladle running[J]. Journal of University of Science and Technology Beijing, 2005, 27(2): 235–239. (in Chinese) |
| [6] |
刘青, 田乃媛, 侯文义, 等.
转炉炼钢厂钢包运转的物理模型[J]. 北京科技大学学报, 1999, 21(4): 338–341.
LIU Qing, TIAN Naiyuan, HOU Wenyi, et al. Physical model of ladle cycling for converter plant[J]. Journal of University of Science and Technology Beijing, 1999, 21(4): 338–341. (in Chinese) |
| [7] |
黄帮福, 田乃媛, 李广双.
钢包管理系统的设计与实现[J]. 冶金自动化, 2011, 35(1): 41–68.
HUANG Bangfu, TIAN Naiyuan, LI Guangshaung, et al. Design and implementation of ladle management system[J]. Metallurgical Industry Automation, 2011, 35(1): 41–68. (in Chinese) |
| [8] | KESHARI K K, MUKHOPADHYAY B, DAS P C. Superheat control with efficient ladle management[C]//Proceedings of 14th IAS Steelmaking conference, 2003, San Nicolas, Argetina.[S.l.]:[S.n.], 2003:395-400. |
| [9] |
贺东风, 于港, 徐安军, 等.
基于精准设计的甘特图组合产能核算[J]. 北京科技大学学报, 2010, 32(12): 1618–1622.
HE Dongfeng, YU Gang, XU Aanjun, et al. Productivity calculation using Gantt chart combination based on precise design[J]. Journal of University of Science and Technology Beijing, 2010, 32(12): 1618–1622. (in Chinese) |
| [10] |
王金明, 张坤, 吕胜会.
运用甘特图确定不锈钢连浇炉数[J]. 山东冶金, 2009, 31(5): 83–85.
WANG Jinming, ZHANG Kun, LÜ Shenghui. Determining stainless steel continuous casting heats by Gantt chart[J]. Shandong Metallurgy, 2009, 31(5): 83–85. (in Chinese) |
| [11] | ANGLANI A, GRIECO A, PACELLA M, et al. Object-oriented modeling and simulation of flexible manufacturing systems:a rule-based procedure[J]. Simulation Modeling Practice and Theory, 2002, 10(10): 209–234. |
| [12] | 李永先. 车辆路径问题的仿真模型及优化仿真研究[D]. 大连: 大连理工大学, 2007. |
 2013, Vol. 36
2013, Vol. 36


