2. 中国航天科技集团川南机械厂, 四川 泸州 646003
2. Chuannan Machinery Manufacturing Plant of China Aerospnce Science and Technology Corporation, Luzhou Sichuan, 646003, China
中国机械加工系统量大,耗电总量惊人[1];Gutowski的研究表明机床能量消耗总量所带来的环境排放十分巨大[2],因此对机床的能量消耗研究具有十分重要的意义。由文献[1, 3]可知,机床能耗包括机床空载能耗、切削能耗和附加载荷损耗3大部分,其中空载能耗在机床空载运行和加工过程中均存在,深入了解机床空载能耗特性是研究整个机床能耗特性的主要课题之一。在机床空载能耗研究方面,刘飞等人[1]建立了普通机床主传动系统的功率模型,揭示了普通机床主传动系统的空载功率与转速近似成二次函数关系;施金良[4]对数控机床变频调速运行过程中的能量特性进行了研究,建立了变频调速主轴系统的功率平衡方程;但是上述研究都是针对机床主传动系统的空载功率特性。
对机床进给系统而言,国内外目前主要集中在进给系统的动力学分析[5-6]、热变形分析[7-8],以及摩擦特性及补偿[9]等方面,关于进给系统的能耗特性研究较少。现代数控机床进给系统具有能耗源多,能耗环节多的特点。能耗源多的特点主要表现在数控机床通常有3个以上进给轴电机;能耗环节多的特点表现在每个轴通常由控制系统,交流伺服电机(permanent magnet synchronous motor,PMSM)以及机械传动系统等环节组成,其中每个环节能耗规律均十分复杂。Kordonowy[10]运用统计方法对不同类型机床的进给系统能耗进行了统计分析,得出了进给系统占机床总能耗的统计结果,但是没有对机床进给系统的每个环节能耗规律进行定量分析。一般而言,提高进给轴速度可以缩短机床加工时间,提高效率,但是进给速度的改变也影响了机床进给轴的功率特性。实时监控机床进给系统的能耗效率需要其空载功率的定量特性信息,因此对进给系统的功率特性建模和空载特性研究十分重要。
针对数控机床进给系统功率特性由于能耗环节多能耗规律复杂导致难以建模的问题,笔者在结合PMSM电机功率特性,机械传动系统动力学特性的基础上,推导出整个进给系统的功率消耗模型,并运用此模型分析了影响空载功率的主要因素。最后在3轴数控铣床进行了测试,实验结果证明了理论分析的有效性。
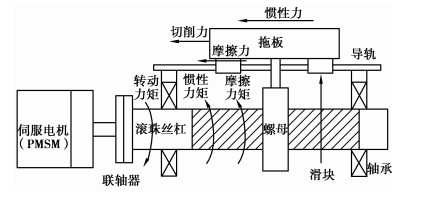
1 进给系统的功率模型数控机床进给系统的典型结构包含永磁同步电机(permanent magnet synchronous motor,PMSM)和机械传动部分,如图 1所示,其中传动部分包括联轴器、滚轴丝杠、螺母、导轨、工作台等。因此,进给系统是一个典型的机电一体化系统,能耗环节多,每个功率环节复杂,其中伺服电机就包含定子铜损、铁损、机械损耗和杂散损耗等[11],机械传送部分包含库伦摩擦损耗和黏性摩擦损耗等[1]。本节在分析各个功率消耗环节的基础上提出进给系统的总体功率模型。
|
图 1 数控车床进给系统结构示意图 |
| $ \begin{array}{l} {P_{{\rm{in}}}} = {P_{\rm{c}}} + {P_{\rm{i}}} + {P_{\rm{m}}} + {P_{\rm{s}}} + {P_{{\rm{out}}}}\\ \;\;\;\;\; = {R_{\rm{a}}}\left( {i_{\rm{d}}^2 + i_{\rm{q}}^2} \right) + \frac{{\omega _{\rm{e}}^2\left( {\psi _{\rm{d}}^2 + \psi _{\rm{q}}^2} \right)}}{{{R_{\rm{i}}}}} + {\omega _{\rm{e}}}{K_{\rm{e}}}{i_{\rm{q}}}, \end{array} $ | (1) |
| $ {\omega _{\rm{e}}}{K_{\rm{e}}}{i_{\rm{q}}} = {P_{\rm{m}}} + {P_{\rm{s}}} + {P_{{\rm{out}}}}, $ | (2) |
| $ \sqrt {i_{\rm{d}}^2 + i_{\rm{q}}^2} = \sqrt 3 {I_{\rm{s}}}, $ | (3) |
|
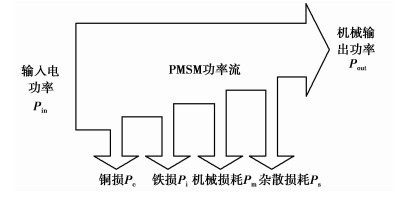
图 2 PMSM的功率模型[10] |
式中:Ra为定子绕组电阻;id为定子电流直轴分量;iq为定子电流交轴分量;Is为定子相电流有效值;Ke为电磁转矩系数;ωe为电机电磁场角速度;ψd为磁通量直轴分量;ψq为磁通量交轴分量;Pc为定子铜损;Pi为定子铁损;Pm为电机机械损耗;Ps为电机杂散损耗;Pout为电机输出功率。
由式(1)~(3)可知,式(1)中第1项表示伺服电机的定子铜损,第2项表示伺服电机的铁损,第3项表示伺服电机的电磁功率(包含了电机的机械损耗、杂散损耗输出功率)。
1.2 进给轴机械传动系统的功率模型数控机床的进给传动系统如图 1所示,在分析其力学、运动学关系[13]的基础上建立其功率模型。
对电机轴建立动力学方程为
| $ {T_{\rm{m}}} = {J_{\rm{m}}}\frac{{{\rm{d}}{\omega _{\rm{m}}}}}{{{\rm{d}}t}} + {B_{\rm{m}}}{\omega _{\rm{m}}} + {T_1}, $ | (4) |
对联轴器建立动力学方程为
| $ {T_1} = {J_{\rm{a}}}\frac{{{\rm{d}}{\omega _{\rm{m}}}}}{{{\rm{d}}t}} + \frac{1}{{{K_g}}}{T_{{\rm{ls}}}}, $ | (5) |
式(4)、(5)中:Bm为电机阻尼系数;Jm为电机转动惯量;ωm为电机轴转速;Tl为驱动联轴器的扭矩;Ja为联轴器等价转动惯量;Tls为驱动滚珠丝杠的扭矩;Kg为联轴器的传动比。
对滚珠丝杠建立动力学方程为
| $ {T_{{\rm{ls}}}} = {J_{{\rm{ls}}}}\frac{{{\rm{d}}{\omega _{{\rm{ls}}}}}}{{{\rm{d}}t}} + {T_{\rm{t}}}, $ | (6) |
滚珠丝杠的负载扭矩可表示为
| $ {T_{\rm{t}}} = \frac{P}{{2{\rm{ \mathsf{ π} }}}}{F_{\rm{t}}}, $ | (7) |
式(6)、(7)中:ωls为滚珠丝杠的角速度;Ft为工作台受的力,包括切削力、惯性力,以及摩擦力;Tt为克服轴力Ft产生的力矩。
工作台的受力情况表示为
| $ {F_{\rm{t}}} = \left( {{M_{\rm{t}}} + {M_{{\rm{load}}}}} \right)\frac{{{\rm{d}}v}}{{{\rm{d}}t}} + {F_{{\rm{friction}}}} + {F_{{\rm{ext}}}}, $ | (8) |
| $ \begin{array}{*{20}{c}} {{F_{{\rm{friction}}}} = {\mu _{\rm{v}}} \cdot v + {f_{\rm{c}}} \cdot {\mathop{\rm sgn}} \left( v \right)}\\ { = {\mu _{\rm{v}}} \cdot v + {\mu _{\rm{c}}}{\mathop{\rm sgn}} \left( v \right)\left| {{F_{\rm{N}}}} \right|,} \end{array} $ | (9) |
式(8),(9)中:v为工作台的进给速度;Ffriction为工作台与导轨间摩擦力;Fext为加在工作台上的切削力;FN为加载在导轨上的正压力;μv为黏性摩擦系数;μc为库伦摩擦系数;sgn(v)为符号函数,当v为正时,sgn(v)=1;当v为负时,sgn(v)=-1;当v为0时,sgn(v)为0。
工作台进给速度与滚珠丝杠转速之间的关系为
| $ v = P\frac{{{\omega _{{\rm{ls}}}}}}{{2{\rm{ \mathsf{ π} }}}}, $ | (10) |
联轴器的传动比为Kg,则:
| $ {\omega _{\rm{m}}} = {K_{\rm{g}}}{\omega _{{\rm{ls}}}}, $ | (11) |
由方程(10)、(11)可得:
| $ \begin{array}{*{20}{c}} {{T_{\rm{m}}} = {J_{\rm{m}}}\frac{{{\rm{d}}{\omega _{\rm{m}}}}}{{{\rm{d}}t}} + {B_{\rm{m}}}{\omega _{\rm{m}}} + {T_1}}\\ { = \left( {{J_{\rm{m}}} + {J_{\rm{a}}}} \right)\frac{{{\rm{d}}{\omega _{\rm{m}}}}}{{{\rm{d}}t}} + {B_{\rm{m}}}{\omega _{\rm{m}}} + }\\ {\frac{1}{{{K_{\rm{g}}}}}\left( {{J_{{\rm{ls}}}}\frac{1}{{{K_{\rm{g}}}}}\frac{{{\rm{d}}{\omega _{\rm{m}}}}}{{{\rm{d}}t}} + } \right.}\\ {\left. {\frac{P}{{2{\rm{ \mathsf{ π} }}}}\left( {\left( {{M_{\rm{t}}} + {M_{{\rm{load}}}}} \right)\frac{P}{{2{\rm{ \mathsf{ π} }}{K_g}}}\frac{{{\rm{d}}{\omega _{\rm{m}}}}}{{{\rm{d}}t}} + {F_{{\rm{friction}}}} + {F_{{\rm{ext}}}}} \right)} \right) = }\\ {\left( {{J_{\rm{m}}} + {J_{\rm{a}}} + \frac{{{J_{{\rm{ls}}}}}}{{K_g^2}} + \frac{{{P^2}}}{{4{{\rm{ \mathsf{ π} }}^2}K_g^2}}\left( {{M_{\rm{t}}} + {M_{{\rm{load}}}}} \right)} \right)\frac{{{\rm{d}}{\omega _{\rm{m}}}}}{{{\rm{d}}t}} + }\\ {{B_{\rm{m}}}{\omega _{\rm{m}}} + \frac{P}{{2{\rm{ \mathsf{ π} }}{K_g}}}\left( {{F_{{\rm{friction}}}} + {F_{{\rm{ext}}}}} \right)。} \end{array} $ | (12) |
工作台受到的正压力为工作台与工件的重力,即
| $ \begin{array}{l} {F_{{\rm{friction}}}} = {\mu _{\rm{v}}} \cdot v + {f_{\rm{c}}} \cdot {\mathop{\rm sgn}} v\\ \;\;\;\;\;\;\;\;\; = {\mu _{\rm{v}}} \cdot v + {\mu _{\rm{c}}}\left( {{M_{\rm{t}}} + {M_{{\rm{load}}}}} \right){\mathop{\rm sgn}} v, \end{array} $ | (13) |
式中:Mt为工作台的质量;Mload为工作台上负载工件质量。
将方程(11)带入式(12)可得电机输出扭矩模型:
| $ \begin{array}{*{20}{c}} {{T_{\rm{m}}} = \left[ {{J_{\rm{m}}} + {J_{\rm{a}}} + \frac{{{J_{{\rm{ls}}}}}}{{K_g^2}} + \frac{{{P^2}}}{{4{{\rm{ \mathsf{ π} }}^2}K_g^2}}\left( {{M_{\rm{t}}} + {M_{{\rm{load}}}}} \right)} \right]\frac{{{\rm{d}}{\omega _{\rm{m}}}}}{{{\rm{d}}t}} + }\\ {\left( {{B_{\rm{m}}} + \frac{{{P^2}{\mu _{\rm{v}}}}}{{4{{\rm{ \mathsf{ π} }}^2}K_g^2}}} \right){\omega _{\rm{m}}} + \frac{{P{\mu _{\rm{c}}}{\mathop{\rm sgn}} \left( {{\omega _{\rm{m}}}} \right)}}{{2{\rm{ \mathsf{ π} }}{K_g}}}\left( {{M_{\rm{t}}} + {M_{{\rm{load}}}}} \right) + \frac{{P{F_{{\rm{ext}}}}}}{{2{\rm{ \mathsf{ π} }}{K_g}}}。} \end{array} $ | (14) |
当机床的进给速度稳定时
| $ \begin{array}{*{20}{c}} {{P_{{\rm{out}}}} = {T_{\rm{m}}} \cdot {\omega _{\rm{m}}} = }\\ {\left( {{B_{\rm{m}}} + \frac{{{P^2}{\mu _{\rm{v}}}}}{{4{{\rm{ \mathsf{ π} }}^2}K_g^2}}} \right)\omega _{\rm{m}}^2 + }\\ {\left[ {\frac{{P{\mu _{\rm{c}}}{\mathop{\rm sgn}} \left( {{\omega _{\rm{m}}}} \right)}}{{2{\rm{ \mathsf{ π} }}{K_g}}}\left( {{M_{\rm{t}}} + {M_{{\rm{load}}}}} \right) + \frac{{P{F_{{\rm{ext}}}}}}{{2{\rm{ \mathsf{ π} }}{K_g}}}} \right]{\omega _{\rm{m}}}。} \end{array} $ | (15) |
由式(1)~(3)、(15)可得:
| $ {P_{{\rm{in}}}} = 3{R_{\rm{a}}}I_{\rm{s}}^2 + \frac{{\omega _{\rm{e}}^2\left( {\psi _{\rm{d}}^2 + \psi _{\rm{q}}^2} \right)}}{{{R_{\rm{i}}}}} + {\omega _{\rm{e}}}{K_{\rm{e}}}{i_{\rm{q}}}。$ | (16) |
式(16)中第2项是铁损功率,第3项电磁功率包含了机械损失功率、杂散损耗和机械输出功率。但是2项的参数Ri、ψd、ψq、iq均不可以直接测量,为此需进行转换。
在工程实践以及电机技术说明书中[14],电机扭矩系数表示的是电磁转矩和相电流有效值之比,而且电磁转矩TeN包含了电机机械损失、杂散损耗、机械输出转矩和铁损转矩。同时,在伺服电机的矢量控制中,直轴电流近似为0[15]。
因此将式(16)写成
| $ {P_{{\rm{in}}}} = 3{R_{\rm{a}}}I_{\rm{s}}^2 + {\omega _{\rm{m}}}{T_{{\rm{eN}}}}。$ | (17) |
电机的电磁转矩与电流有如下关系:
| $ {T_{{\rm{eN}}}} = {K_{\rm{T}}}{I_{\rm{s}}}, $ | (18) |
| $ 式中:{T_{{\rm{eN}}}} = {T_{\rm{m}}} + {T_0}, $ | (19) |
式中:T0为电机内部机械损耗转矩、铁损耗转矩、杂散损耗转矩;KT为扭矩系数。
由式(18)、(19)可得:
| $ \begin{array}{*{20}{c}} {{I_{\rm{s}}} = \frac{1}{{{K_{\rm{T}}}}}\left[ {\left( {{B_{\rm{m}}} + \frac{{{P^2}{\mu _{\rm{v}}}}}{{4{{\rm{ \mathsf{ π} }}^2}K_{\rm{g}}^2}}} \right){\omega _{\rm{m}}} + } \right.}\\ {\left. {\frac{{P{\mu _{\rm{c}}}{\mathop{\rm sgn}} \left( {{\omega _{\rm{m}}}} \right)}}{{2{\rm{ \mathsf{ π} }}{K_g}}}\left( {{M_{\rm{t}}} + {M_{{\rm{load}}}}} \right) + {T_0} + \frac{{P{F_{{\rm{ext}}}}}}{{2{\rm{ \mathsf{ π} }}{K_g}}}} \right]。} \end{array} $ | (20) |
其中,令
| $ {{B'}_{\rm{m}}} = \frac{1}{{{K_{\rm{T}}}}}\left( {{B_{\rm{m}}} + \frac{{{P^2}{\mu _{\rm{v}}}}}{{4{{\rm{ \mathsf{ π} }}^2}K_{\rm{g}}^2}}} \right), $ |
| $ {{K'}_{{\rm{eq}}}} = \frac{{P{\mu _{\rm{c}}}}}{{2{\rm{ \mathsf{ π} }}{K_{\rm{g}}}{K_{\rm{T}}}}}, $ |
| $ {{T'}_0} = \frac{{{T_0}}}{{{K_{\rm{T}}}}}, $ |
| $ {T_{\rm{c}}} = \frac{{P{F_{{\rm{ext}}}}}}{{{K_{\rm{T}}}2{\rm{ \mathsf{ π} }}{K_g}}}。$ |
在实际应用中,通常以ωm方向为正方向,则式(20)可转变为
| $ {I_{\rm{s}}} = {{B'}_{\rm{m}}}{\omega _{\rm{m}}} + {{K'}_{{\rm{eq}}}}\left( {{M_{\rm{t}}} + {M_{{\rm{load}}}}} \right) + {{T'}_0} + {T_{\rm{c}}}。$ | (21) |
将式(21)带入式(17)可得进给系统功率模型:
| $ \begin{array}{*{20}{c}} {{P_{{\rm{in}}}} = \left( {3{R_{\rm{a}}}{{B'}_{\rm{m}}}^2 + {K_T}{{B'}_{\rm{m}}}} \right)\omega _{\rm{m}}^2 + }\\ {\left[ {6{R_{\rm{a}}}{{B'}_{\rm{m}}} + {K_{\rm{T}}}} \right]\left[ {{{K'}_{{\rm{eq}}}}\left( {{M_{\rm{t}}} + {M_{{\rm{load}}}}} \right) + } \right.}\\ {\left. {{{T'}_0} + {T_{\rm{c}}}} \right]{\omega _{\rm{m}}} + 3{R_{\rm{a}}}{{\left[ {{{K'}_{{\rm{eq}}}}\left( {{M_{\rm{t}}} + {M_{{\rm{load}}}}} \right) + {{T'}_0} + {T_{\rm{c}}}} \right]}^2}。} \end{array} $ | (22) |
当切削矩Tc等于零时,就可以得到机床进给系统的空载功率:
| $ \begin{array}{*{20}{c}} {{P_{{\rm{in}}}} = \left( {3{R_{\rm{a}}}{{B'}_{\rm{m}}} + {{K'}_T}} \right){{B'}_{\rm{m}}}\omega _{\rm{m}}^2 + }\\ {\left( {6{R_{\rm{a}}}{{B'}_{\rm{m}}} + {{K'}_{\rm{T}}}} \right)\left[ {{{K'}_{{\rm{eq}}}}\left( {{M_{\rm{t}}} + {M_{{\rm{load}}}}} \right) + {{T'}_0}} \right]{\omega _{\rm{m}}} + }\\ {3{R_{\rm{a}}}{{\left[ {{{K'}_{{\rm{eq}}}}\left( {{M_{\rm{t}}} + {M_{{\rm{load}}}}} \right) + {{T'}_0}} \right]}^2}。} \end{array} $ | (23) |
由进给系统空载功率表达式(23)可知:机床进给系统的空载功率随着进给速度和工作台载荷工件质量的变化而变化。
2.1 进给系统空载功率与伺服电机角速度的关系由式(23)可知,进给系统功率Pin是转速ωm的二次函数。功率对转速求导可得:
| $ \frac{{\partial {P_{\rm{u}}}}}{{\partial {\omega _{\rm{m}}}}} = \frac{{\partial {P_{\rm{u}}}}}{{\partial {I_{\rm{s}}}}} \cdot \frac{{\partial {I_{\rm{s}}}}}{{\partial {\omega _{\rm{m}}}}} = {{B'}_{\rm{m}}}\left( {6{I_{\rm{s}}}{R_{\rm{a}}} + {K_{\rm{T}}}{\omega _{\rm{m}}}} \right)。$ | (24) |
当ωm>0时,
由式(23)可知,进给系统功率Pu是载荷质量Mload的一次函数。功率对载荷质量求导可得:
| $ \begin{array}{l} \frac{{\partial {P_{\rm{u}}}}}{{\partial {M_{{\rm{load}}}}}} = \frac{{\partial {P_{\rm{u}}}}}{{\partial {I_{\rm{s}}}}} \cdot \frac{{\partial {I_{\rm{s}}}}}{{\partial {M_{{\rm{load}}}}}}\\ \;\;\;\;\;\;\;\;\;\; = {{K'}_{{\rm{eq}}}}\left( {6{I_{\rm{s}}}{R_{\rm{a}}} + {K_{\rm{T}}}{\omega _{\rm{m}}}} \right) > 0。\end{array} $ | (25) |
式(24)表明输入功率Pu随着Mload的增加而单调递增。
由式(10)、式(11)、式(25)可得
| $ \begin{array}{l} \frac{{\partial {P_{\rm{u}}}}}{{\partial {M_{{\rm{load}}}}}} = {{K'}_{{\rm{eq}}}}\left( {6{I_{\rm{s}}}{R_{\rm{a}}} + {K_{\rm{T}}}{\omega _{\rm{m}}}} \right)\\ = {{K'}_{{\rm{eq}}}}\left( {6{I_{\rm{s}}}{R_{\rm{a}}} + {K_{\rm{T}}} \cdot {K_{\rm{g}}} \cdot \frac{{2{\rm{ \mathsf{ π} }}}}{P} \cdot v} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\; = 6{{K'}_{{\rm{eq}}}}{I_{\rm{s}}}{R_{\rm{a}}} + {\mu _{\rm{c}}} \cdot v。\end{array} $ |
由此可知,空载功率随负载质量变化取决于6K′eqIsRa,而μc·v不变。其中
对一台数控机床(PL700)X轴进给系统进行仿真分析,该机床的基本参数如表 1所示。
| 表 1 PL700X轴的伺服电机以及进给系统的相关参数 |
由于式(22)中B′m、K′eq、T′0等参数无法预先已知或者不准确,影响功率的仿真研究。笔者利用电流与转速的关系对参数B′m、K′eq、T′0进行辨识。下面对B′m、K′eq、T′0参数辨识的原理进行简要介绍。
由于空载电流Is与转速ωm满足如下关系:
| $ {I_{{\rm{s0}}}} = {{B'}_{\rm{m}}}{\omega _{\rm{m}}} + {{K'}_{{\rm{eq}}}}\left( {{M_{\rm{t}}} + {M_{{\rm{load}}}}} \right) + {{T'}_0}。$ | (25) |
将式(25)改写成矩阵格式有:
| $ \left[ {\begin{array}{*{20}{c}} {{\omega _{\rm{m}}}}&{{M_{\rm{t}}} + {M_{{\rm{load}}}}}&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{B'}_{\rm{m}}}}\\ {{{K'}_{{\rm{eq}}}}}\\ {{{T'}_0}} \end{array}} \right] = {I_{{\rm{s0}}}}。$ | (26) |
通过多组实验,用式(27)、式(28)最小二乘法辨识出B′m,K′eq,T′0。
| $ {A_{{\rm{n}} \times 1}}\theta = {b_{{\rm{nl}} \times 1}}, $ | (27) |
| $ \theta = {\left( {{A^{\rm{T}}}A} \right)^{ - 1}}{A^{\rm{T}}}b, $ | (28) |
其中:
| $ A = \left[ {\begin{array}{*{20}{c}} {{\omega _{{\rm{m1}}}}}&{{M_{\rm{t}}} + {M_{{\rm{loadl}}}}}&1\\ {{\omega _{{\rm{m2}}}}}&{{M_{\rm{t}}} + {M_{{\rm{loadl}}}}}&1\\ \cdots&\cdots&\cdots \\ {{\omega _{{\rm{mn}}}}}&{{M_{\rm{t}}} + {M_{{\rm{loadl}}}}}&1\\ \cdots&\cdots&\cdots \\ {{\omega _{{\rm{m1}}}}}&{{M_{\rm{t}}} + {M_{{\rm{loadl}}}}}&1\\ {{\omega _{{\rm{m2}}}}}&{{M_{\rm{t}}} + {M_{{\rm{loadl}}}}}&1\\ \cdots&\cdots&\cdots \\ {{\omega _{{\rm{mn}}}}}&{{M_{\rm{t}}} + {M_{{\rm{loadl}}}}}&1 \end{array}} \right]\left( {n \ge 3,l \ge 3} \right), $ |
| $ b = {\left[ {\begin{array}{*{20}{c}} {{I_{{\rm{s0}},11}}}&{{I_{{\rm{s0}},21}}}& \cdots &{{I_{{\rm{s0}},{\rm{n1}}}}}& \cdots &{{I_{{\rm{s0}},11}}}&{{I_{{\rm{s0}},21}}}& \cdots &{{I_{{\rm{s0}},{\rm{n1}}}}} \end{array}} \right]^{\rm{T}}}。$ |
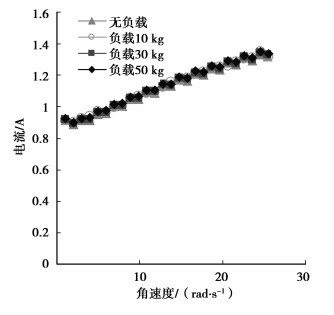
在本次实验中,分别取n=26(进给速度的取值范围为从150~3 900 mm/min。150 mm/min为一档),l=4(工作台无负载、负载10 kg工件、负载30 kg工件,负载50 kg),做了26×4次实验。电流与转速的曲线如图 3所示,辨识出该机床的参数分别为:B′m=0.191,K′eq=3.4×10-5,T′0=0.802。
|
图 3 不同工件质量下电流角速度曲线 |
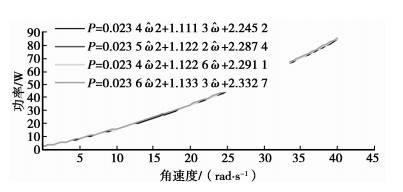
通过辨识结果可以看出,K′eq是一个很小的数,因此可以近似认为K′eq(Mt+Mload)为0,功率消耗受质量变化影响不大,符合3.2节推算出K′eq的取值数量级为10-5~10-3的结论。根据辨识出来的B′m,K′eq,T′0及方程(22),对该机床进行仿真分析,如图 4所示,从图 4中可以看出,进给系统的功率消耗值随着进给速度的变化成二次递增关系,同时可以看出,功率消耗受负载影响很小。
|
图 4 进给系统的功率仿真曲线 |
本次实验以上述数控机床PL700为测试对象做验证实验,该机床进给系统电机以及机械传动部分具体参数见表 1。功率测试的仪器为日置3390宽频功率分析仪。
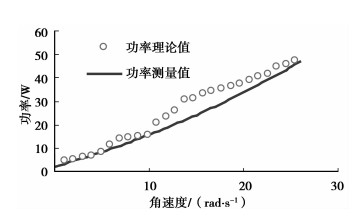
1) 实验将进给速度v在150~3 900 mm/min内(以150 mm/min为一档)测试,每档运行距离为导轨最大运行范围内做一来回运动。重复3次实验,结果取其平均值(如图 5所示)。从图 5可以看出,进给系统与进给速度呈二次函数关系,与1.3节式(22)的表达吻合。
|
图 5 进给系统的功率理论值与测量值比较 |
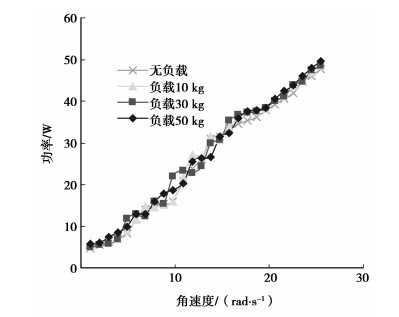
2) 为了验证进给系统功率消耗与负载质量的关系,对负载做了扰动实验(无负载,负载质量10,30,50 kg)。实验结果如图 6所示,从实验结果可以看出,进给系统功率消耗值随进给速度的增加而单调递增。当工作台上负载变化时,功率的消耗值并没有太大的变化,与仿真时得出的结果一致,同时可以看出,功率消耗受负载影响很小,符合2.2节负载质量对功率消耗影响较小的分析。
|
图 6 不同负载下的进给系统功率 |
笔者首先建立了数控机床进给系统的功率模型,然后分析了空载功率与进给速度,负载质量的关系,得出了以下结论:
1) 数控机床进给系统功率是关于进给速度和切削矩(或切削力)的二次函数,如式(22)所示。可以通过不同转速不同切削参数的实验确定此函数关系。
2) 数控机床进给系统的空载功率与进给速度呈单调递增的二次函数关系,如式(23)所示。在工程应用中,可以通过测量不同转速不同负载质量时的空载功率拟合出该二次曲线。一旦辨识出此特性函数,只要知道进给速度就可以确定进给系统的空载功率,进而实时监控机床进给系统的能耗效率等。
3) 理论分析和实验结果均表明负载质量与对进给系统空载功率影响很小,其影响系数在10-5~10-3之间。在一定条件下可以忽略质量变化对空载功率的影响。
5 致谢感谢成都普瑞斯数控机床有限公司和北京法朗克公司为本研究提供的机床和伺服电机的相关技术参数。
| [1] | 刘飞, 徐宗俊, 但斌. 机械加工系统能量特性及其应用[M]. 北京: 机械工业出版社, 1995. |
| [2] | GUTOWSKI T, DAHMUS J, THIRIEZ A. Electrical energy requirements for manufacturing processes[EB/OL]//Proceedings of the 13th CIRP International Conference on Life Cycle Engineering, May 31-June 2, 2006, Leuven, Belgium.[2011-05-21] http://web.mit.edu/2.813/www/readings/Gutowski-CIRP.pdf |
| [3] | HU S H, LIU F, HE Y, et al. Characteristics of additional load losses of spindle system of machine tools[J]. Journal of Advanced Mechanical Design, Systems, and Manufacturing, 2010, 4(7): 1221–1233. DOI:10.1299/jamdsm.4.1221 |
| [4] |
施金良, 刘飞, 许弟建, 等.
变频调速数控机床主传动系统的功率平衡方程[J]. 机械工程学报, 2010, 46(3): 118–124.
SHI Jinliang, LIU Fei, XU Dijian, et al. Power balance equation about the numerical control machine tool's main driver system driven by variable voltage variable frequency[J]. Chinese Journal of Mechanical Engineering, 2010, 46(3): 118–124. (in Chinese) |
| [5] | WHALLEY R, EBRHAIMI M, AMMER A A A. Machine tool axis dynamics[J]. Institution of Mechanical Engnieers, Part C:Journal of Mechanical Engineering Science, 2006, 220(4): 403–419. DOI:10.1243/09544062C15904 |
| [6] |
丁文正, 黄筱调, 汪木兰.
面向大型机床再制造的进给系统动态特性[J]. 机械工程学报, 2011, 46(3): 135–140.
DING Wenzheng, HUANG Xiaodiao, WANG Mulan. Dynamic characteristics of feed system for large-scale machine tool remanufacturing[J]. Chinese Journal of Mechanical Engineering, 2011, 46(3): 135–140. (in Chinese) |
| [7] |
夏军勇, 胡友民, 吴波, 等.
热弹性效应分析与机床进给系统热动态特性建模[J]. 机械工程学报, 2010, 46(15): 191–198.
XIA Junyong, HU Youmin, WU Bo, et al. Analysis on thermoelastic domino effect and modeling on thermal dynamic characteristic of mahine tools feed system[J]. Journal of Mechanical Engineering, 2010, 46(15): 191–198. (in Chinese) |
| [8] | WU C H, KUNG Y T. Thermal analysis for the feed drive system of a CNC machine center[J]. International Journal of Machine Tools & Manufacture, 2003, 43(15): 1521–1528. |
| [9] | ERKORKMAZ K, ALTINTAS Y. High speed CNC system design.Part Ⅱ:modeling and identification of feed drives[J]. International Journal of Machine Tools & Manufacture, 2001, 41(10): 1487–1509. |
| [10] | KORDONOWY D N. A power assessment of machining tools[EB/OL].Massachusetts Institute of Technology, 2002[2011-05-12].http://18.7.29.232/handle/1721.1/31108#files-area . |
| [11] | SENJYU T, KUWAE Y, URASAKI N, et al. Accurate parameter measurement for high speed permanent magnet synchronous motors[C]//Proceedings of the 32nd Annual Power Electronics Specialists Conference, June 17-21, 2001, Vancouver, Canada. Piscataway:IEEE Press, 2001(2):772-777. |
| [12] | URASAKI N, SENJYU T, UEZATOK. A novel calculation method for iron loss resistance suitable in modeling permanent-magnet synchronous motors[J]. IEEE Transactions on Energy Conversion, 2003, 18(1): 41–47. DOI:10.1109/TEC.2002.808329 |
| [13] | JEONG Y H, MIN B K, CHO D W, et al. Motor current prediction of a machine tool feed drive using a component-based simulation model[J]. International Journal of Precision Engineering and Manufacturing, 2010, 11(4): 597–606. DOI:10.1007/s12541-010-0069-1 |
| [14] |
段卫国, 杨飞中, 程智, 等.
交流伺服电动机的电势系数和转矩系数-样本数据的解读[J]. 伺服控制, 2007(3): 20–22, 26.
DUAN Weiguo, YANG Feizhong, CHENG Zhi, et al. AC servo motor's potential coefficient and torque coefficient -the interpretation of sample data[J]. Servo Control, 2007(3): 20–22, 26. (in Chinese) |
| [15] | 王成元, 夏加宽, 杨俊友, 等. 电机现代控制技术[M]. 北京: 机械工业出版社, 2006. |
| [16] | 机械工程手册电机工程手册编辑委员会. 机械工程手册[M]. 2版. 北京: 机械工业出版社, 1997. |
 2013, Vol. 36
2013, Vol. 36



