收稿日期: 2013-07-30
基金项目: 中央高校基本科研业务费资助项目(XDJK2011C068)
Improvement and simulation on direct torque control system of permanent magnet synchronous motor
College of Engineering and Technology, Southwest University, Chongqing 400715, China
直接转矩控制(DTC)是继矢量控制技术之后的又一新型高效变频调速技术。在定子坐标系下,应用定子磁链定向,利用离散Band-Band进行调节,产生逆变器脉宽调制信号,对电机的磁链和转矩进行直接控制,获得电机转矩的高动态性能,近些年来这种控制方法已被广泛应用于永磁同步电机(PMSM)[1]。传统PMSM-DTC采用转矩、磁链滞环控制器和基于60°定子磁链位置信号,按照设定规则从预先制定的开关表中选取相应的电压空间矢量对永磁同步电机转矩、磁链进行直接控制,这种控制系统结构简单,不需要复杂的坐标变换,通过对磁链和转矩的直接跟踪,实现脉宽调制和系统的高动态性能,对电机参数不敏感,系统鲁棒性强[2]。但大量的分析和实践表明,这种控制方法存在较大缺陷,其中磁链、转矩脉动较大,逆变器开关频率不恒定已成为限制其在工业中广泛应用的最主要原因[3-5]。针对这一问题,国内外学者进行了广泛的研究,文献[6]中将磁链细分法引入PMSM-DTC,定子磁链平面被分成12个扇区,矢量选择更加细致;文献[7-9]将零电压矢量引入到转矩调节器中,并对零矢量的作用进行了详细的理论分析,指出在电机低速运行时,零电压矢量对转矩的影响很小,可以用来保持转矩,但当电机高速运行时,零电压矢量会起到减小转矩的作用;文献[10-11]分析了电压矢量对电磁转矩的作用,给出了不合理转矩脉动产生的根源,对空间电压矢量的选择条件做了细化,并由此改进开关表。这些方法都可在一定程度上改善系统的静态性能,但是由于可供选择的电压空间矢量被局限为只有8个,因此都无法在本质上完全消除磁链、转矩期望值与实际值之间的误差。2002年tang等[12]将空间矢量调制(SVM)技术引入到PMSM-DTC中,即在一个开关周期内,通过零矢量和相邻两个基本电压矢量合成所需的任意目标电压矢量,从而实现目标电压矢量的连续线性可调。从仿真和实验结果来看,这种方法在有效减少转矩脉动,改善直接转矩控制系统性能的基础上,同时保持逆变器开关频率恒定。但目前这类控制系统多采用两个PI调节器(一个用以调节磁链,另一个用来调节转矩)[13-15],用于计算SVM所需要的目标电压矢量,在提高系统稳态性能的同时导致系统结构复杂,动态性能变差,参数调节更加困难。
笔者在对永磁同步电机数学模型进行深入分析的基础上,将一简单的SVM策略引入PMSM-DTC系统中,设计一个只包含单个速度PI调节的基于空间矢量调制的PMSM-DTC系统,文中阐述了系统的构成原理,详细介绍了各个模块的构成。最后,针对一款极隐式永磁同步电机建立仿真模型,给出仿真结果,并与传统DTC控制效果进行对比。对比结果表明,该方案能有效减小永磁同步电机磁链、转矩脉动,同时保证逆变器的开关频率恒定。即在不增加系统复杂性的条件下,保持系统优异的动态响应特性,有效提高系统的稳态性能。笔者所用电机参数为
|
$
{{\psi }_{\text{PM}}}=0.2\ \text{Wb, }{{L}_{\text{d}}}\text{=}{{L}_{\text{q}}}\text{=}6.0\text{mH, }
$
|
|
$
{{R}_{\text{s}}}\text{=}0.975\ \Omega, J\ \text{=}1.0\times {{10}^{\text{-}3}}\text{kg}\centerdot {{\text{m}}^{2}}, p=4。$
|
1 永磁同步电动机的数学模型
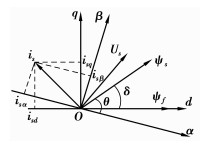
永磁同步电机矢量图如图 1所示,忽略磁滞损耗和电机涡流,假定转子无阻尼绕组,则永磁同步电机在d-q轴转子坐标系下的电压、磁链和电磁转矩方程[16]为
|
$
{{\psi }_{\text{d}}}={{L}_{d}}{{i}_{d}}+{{\psi }_{f}},
$
|
(1) |
|
$
{{\psi }_{q}}={{L}_{q}}{{i}_{q}},
$
|
(2) |
|
$
{{u}_{d}}=\frac{\text{d}{{\psi }_{d}}}{\text{d}t}-\omega {{\psi }_{q}}+{{R}_{s}}{{i}_{d}},
$
|
(3) |
|
$
{{u}_{q}}=\frac{\text{d}{{\psi }_{q}}}{\text{d}t}-\omega {{\psi }_{d}}+{{R}_{s}}{{i}_{q}},
$
|
(4) |
|
$
\begin{align}
&{{T}_{e}}=\frac{3}{2}\centerdot p\centerdot \left( {{\psi }_{q}}\times {{i}_{s}} \right) \\
&\ \ \ \ =\frac{3p\left| {{\psi }_{s}} \right|}{4{{L}_{d}}{{L}_{q}}}\left[2{{\psi }_{f}}{{L}_{q}}\sin \delta-\left| {{\psi }_{s}} \right|\left( {{L}_{d}}-{{L}_{q}} \right)\sin 2\delta \right], \\
\end{align}
$
|
(5) |
|
$
J\frac{\text{d}{{\omega }_{m}}}{\text{d}t}={{T}_{e}}-{{T}_{L}}-B{{\omega }_{m}}。$
|
(6) |
式中:ψd、ψq为定子磁链ψs的d、q轴分量;Ld、Lq为定子绕组d、q轴电感;ψf为永磁体磁链;ud、uq为定子电压Us的d、q轴分量;id、iq为定子电流is的d、q轴分量;Rs为定子电阻;p为电机转子极对数;Te为电机电磁转矩;δ为定、转子磁链之间的夹角,称转矩角;TL为负载转矩;J为转动惯量;B为摩擦系数;ωm为电机转子角速度。针对笔者采用的表面式永磁同步电机,存在Ls=Ld=Lq,转子永磁体产生的磁链ψf为一恒定值ψPM,则式(5)可简化为
|
$
{{T}_{e}}=\frac{3p\left| {{\psi }_{s}} \right|{{\psi }_{PM}}{{L}_{q}}\sin \delta }{2L_d}。$
|
(7) |
式(7)说明,在恒定负载、稳态运行时,定子、转子磁链都以同步速旋转,此时δ为恒值;瞬态时,δ则因定子、转子的旋转速度不同而不断改变。直接转矩控制即是在尽量保持定子磁链幅值|ψs|恒定的前提下,通过改变转矩角δ来控制电机电磁转矩Te。
2 转矩角δ的简化计算
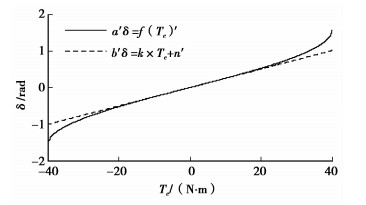
由式(7)不难看出转矩Te与定子磁链的幅值|ψs|及转矩角δ间存在密切的关系。针对笔者采用的永磁同步电机参数,在保持|ψs|≡ψPM的前提下,以电磁转矩Te为自变量、转矩角δ为因变量画出关系曲线如图 2中曲线a所示,观察曲线a发现在电机输出转矩[-16, 16]范围内,转矩角δ与转矩Te间近似呈线性关系。在转矩[-16, 16]范围内,对曲线a进行线性拟合,得到近似直线b,δ=k×Te+n。对比曲线a和曲线b不难看出在电机允许的输出转矩Te变化范围内,曲线a、b近乎重合。曲线b将转矩角δ与转矩Te近似为线性关系,不但可以清晰地指示出δ的实时变化,还可替代文献[13-15]中使用的转矩PI调节器,提高系统的动态特性,简化参数调节过程。
3 基于SVM的PMSM-DTC系统
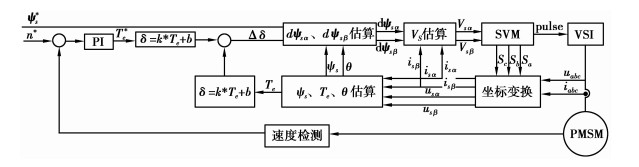
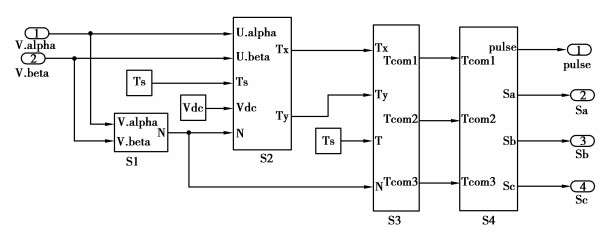
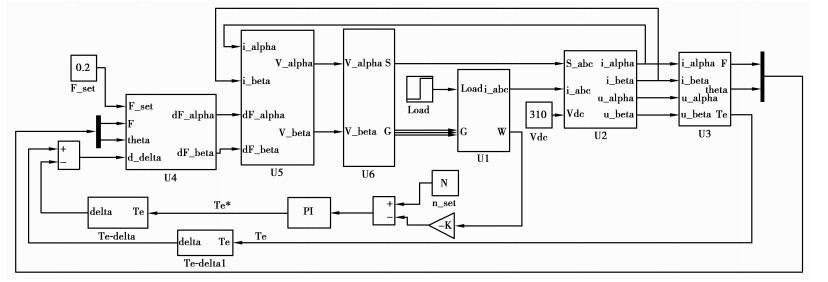
受逆变器结构的限制,其同一桥臂上提供的电压VDC为恒值,因而基本空间电压矢量也比较固定,只能提供6个(V1~V6)非零矢量和2个(V0、V7)零矢量。传统的直接转矩控制系统是经过多次滞环比较,通过增加逆变器开关频率来无限趋进。这种控制方法一方面使电机在运行中产生较大转矩和磁链脉动,另一方面则导致逆变器开关频率不恒定。为解决这一问题,本系统在不增加PI回路的前提下,引入空间电压矢量调制概念,即在不改变基本电压矢量,V1~V6非零矢量和V0、V7零矢量的情况下,改变每个采样周期中各电压矢量的作用时间,从而合成理想的电压矢量Vs完成对目标磁链矢量ψs*的调制。系统结构框图如图 3所示。
PI调节器输出的转矩参考值Te*与转矩估算值Te之间存在误差dTe,为了能够补偿误差dTe,定子磁链相位角增加Δδ。由前面的分析可知针对笔者所用的永磁同步电机,在输出转矩[-16, 16]范围内,可将转矩角δ与转矩Te间的关系近似为线性δ=k×Te+n。由Δδ得到定子磁链目标磁链矢量ψs*。将定子磁链估算值ψs与ψs*进行对比,得到误差dψs。通过电压空间矢量Vs估算模块计算出补偿这一误差所需定子电压分量Vsα和Vsβ。系统采用一个SVM单元合成该目标电压空间矢量,将调制中由该单元产生的逆变器开关信号pulse送入电压源型逆变(VSI)单元,最终实现转矩、磁链的准确、平滑控制。
3.1 Te、ψs和θ的估算
在PMSM的直接转矩控制系统中,定子磁链矢量的幅值和角位置、转矩是在定子α-β坐标系下实现的,如图 1所示,可由下列式子来观测。
|
$
\left\{ \begin{align}
&{{\psi }_{s\alpha }}=\int{\left( {{u}_{\alpha }}-{{R}_{s}}{{i}_{s\alpha }} \right)\text{d}t, } \\
&{{\psi }_{s\beta }}=\int{\left( {{u}_{\beta }}-{{R}_{s}}{{i}_{s\beta }} \right)\text{d}t, } \\
\end{align} \right.
$
|
(8) |
|
$
\left| {{\psi }_{s}} \right|=\sqrt{\psi _{_{s\alpha }}^{2}+\psi _{_{s\beta }}^{2}},$
|
(9) |
|
$
\theta =\arctan \left( {{\psi }_{s\alpha }}/{{\psi }_{s\beta }} \right),
$
|
(10) |
|
$
{{T}_{e}}=\frac{3}{2}p\left( {{\psi }_{s\alpha }}{{i}_{s\beta }}-{{\psi }_{s\beta }}{{i}_{s\alpha }} \right)。$
|
(11) |
其中下标α、β为各量在定子α-β坐标系α、β轴上的分量,θ为定子磁链的相位角。
3.2 ψs误差估算及目标电压矢量Vs估计
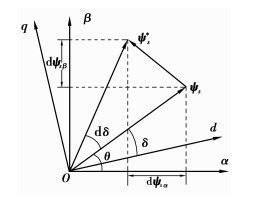
定子磁链的参考矢量ψs*与定子磁链的当前观测值ψs之间存在的矢量误差dψs,如图 4所示。
|
$
\left\{ \begin{array}{l}
{\text{d}}{\mathit{\boldsymbol{\psi }}_{s\alpha }} = {\psi _{sf}}\left( {\cos \theta + {\text{d}}\delta } \right) - {\psi _s}\cos \theta \\
{\text{d}}{\mathit{\boldsymbol{\psi }}_{s\beta }} = {\psi _{sf}}\left( {\cos \theta + {\text{d}}\delta } \right) - {\psi _s}\cos \theta
\end{array} \right.,
$
|
(12) |
将定子磁链的误差矢量dψs送入Vs估算单元计算出为消除转矩、磁链误差所需的目标电压矢量Vs,Vs的幅值和相位角ϕ,计算方法如下:
|
$
\left\{ \begin{array}{l}
{V_{s\alpha }} = d{\psi _{s\alpha }}/{T_s} + {R_s}{i_{s\alpha }}\\
{V_{s\beta }} = d{\psi _{s\beta }}/{T_s} + {R_s}{i_{s\beta }}
\end{array} \right.,
$
|
(13) |
|
$
\left| {{\mathit{\boldsymbol{V}}_s}} \right| = \sqrt {V_{_{s\alpha }}^2 + V_{_{s\beta }}^2},
$
|
(14) |
|
$
\phi = \arctan \left( {{V_{s\beta }}/{V_{s\alpha }}} \right)
$
|
(15) |
3.3 SVM单元组成
采用SVM的目标是利用逆变器固有的基本空间矢量合成所需的目标电压空间矢量。电压源型逆变器(VSI)有8个基本空间电压矢量,合成目标电压矢量Vs,即
|
$
\left\{ \begin{array}{l}
{\mathit{\boldsymbol{V}}_n}{T_n} + {\mathit{\boldsymbol{V}}_{n + 1}}{T_{n + 1}} + {\mathit{\boldsymbol{V}}_0}{T_0} = {\mathit{\boldsymbol{V}}_s}{T_s}, \\
{T_n} + {T_{n + 1}} + {T_0} = {T_s}。\end{array} \right.
$
|
(16) |
其中,Ts为系统采样周期,即VSI逆变器开关周期;T0、Tn、Tn+1分别为在一个采样周期中基本空间电压矢量V0、Vn、Vn+1的作用时间。
在仿真模型中,SVM单元包括矢量扇区判断模块S1、基本矢量作用时间计算模块S2、三相功率器件导通时刻计算模块S3以及触发脉冲生成模块S4,其仿真模型如图 5所示。首先根据ϕ值判断出目标电压矢量Vs所在的扇区,判定合成该目标矢量所需的2个非零基本矢量和零矢量;其次计算出零电压矢量和2个基本电压矢量各自作用时间;通过与对称三角波比较输出三相PWM控制信号pulse及开关状态信号Sa、Sb、Sc。
4 系统仿真及结果分析
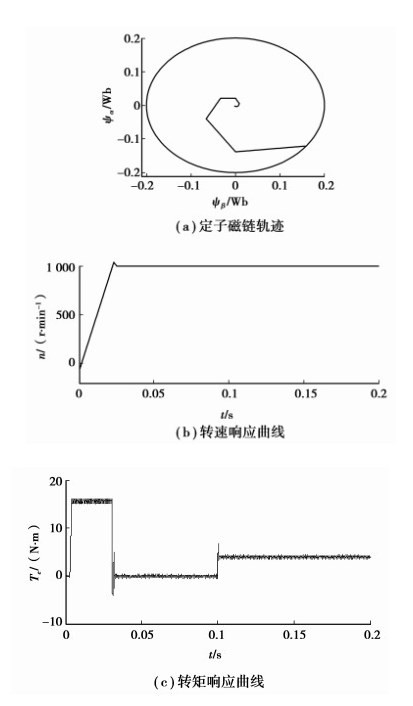
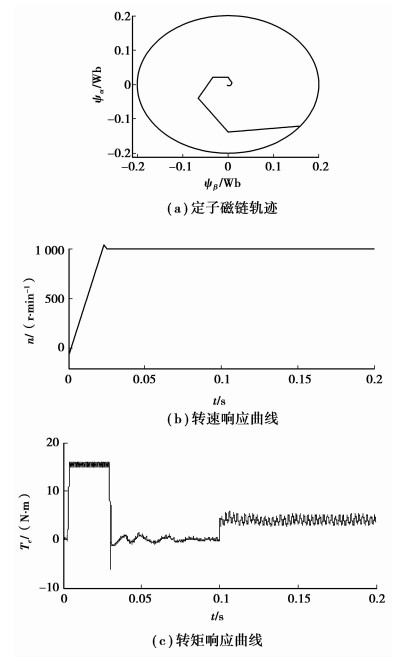
基于上述分析,在Matlab/simulink环境下建立仿真模型如图 6所示。该模型结构与图 2系统原理框图基本一致,整体模型由以下单元组成:逆变电路与PMSM复合模块U1、坐标变换模块U2、Te、ψs和θ估算模块U3、ψs误差估算模块U4、目标电压矢量Vs估算模块U5、SVM模块U6、PI速度控制模块以及Te-δ线性模块。为验证笔者理论分析和系统建模的正确性,针对笔者所采用永磁同步电机在Simulink环境下对模型进行仿真,同时给出了常规DTC的仿真结果以进行比较。仿真条件设置如下:功率器件开关周期Ts=2 ms,在PI控制环节设置限幅值±16 N·m,摩擦系数B为零,直流母线电压VDC=310 V,定子磁链ψs*=ψPM=0.2Wb。电机空载以额定转矩启动,从零转速加速到额定转速1 000 r/min;稳态运行过程中T=0.1 s时突加负载至4 N·m。
系统仿真结果如图 7、图 8所示,图 7(a)~(c)和图 8(a)~(c)分别对比了SVM-DTC与传统DTC两种控制系统的仿真结果。从图中可以看出,系统空载启动时,从零转速加速到额定转速1 000 r/min,大约需要30 ms,与常规直接转矩控制的启动时间相差不大,上升时间都非常短,超调量非常小仅0.1%左右,这正是直接转矩控制系统的突出优点。从转矩和磁链的响应波形来看,两种系统的动态响应都非常快,进入稳态运行以后相对于常规直接转矩控制,基于SVM的PWM-DTC系统的转矩和磁链波动更小。稳态运行过程中突加负载,两种系统的转矩响应都很快,约为1.0 ms,负载变化时转速波动很小,说明系统抗干扰能力较强。产生上述结果的根本原因在于:常规的PMSM-DTC只能选择8个基本空间电压矢量,通过转矩、磁链滞环来控制定子磁链的运动,而将SVM引入PMSM-DTC系统后,使得逆变器能够输出线性连续的空间电压矢量,消除由于常规PMSM-DTC在各个区域交界处对转矩的控制效果减弱而导致的转矩、磁链出现周期性波动,同时减小稳态运行时转矩、磁链的脉动;其次笔者采用一种简化的基于电压空间矢量调制的直接转矩控制,整个系统只采用一个易于调节的速度PI调节器,故可在保持常规直接转矩控制快速的动态响应的前提下,有效提高系统的稳态运行性能。
5 结语
在对永磁同步电机数学模型深入分析的基础上,提出一种简化的基于SVM的PMSM-DTC系统,即采用电压矢量调制获得空间电压矢量的优化组合,实现转矩和磁链误差的精确补偿,整个系统只采用了一个PI调节器,系统结构简单,参数容易调节,且保证逆变器开关频率恒定。仿真结果表明,这种控制系统在保持优异动态响应特性不变的条件下,有效提高PMSM-DTC系统的稳态运行性能,在保证逆变器开关频率恒定的基础上,达到高性能的直接转矩控制效果。
 2013, Vol. 36
2013, Vol. 36

