由于环境污染、能源匮乏等问题日益严重,电动汽车(electric vehicle,EV)受到越来越广泛的关注。目前,在动力电池等关键技术取得突破之前,续驶里程成为制约电动汽车发展的重要因素。对动力传动系统部件参数的合理匹配是提高电动汽车能耗经济性从而延长续驶里程的重要手段之一。
蓄电池是纯电动汽车唯一的能量来源,除了为动力传动系统提供驱动能量外,还要给电动空调、制动系统和电动助力转向系统等附件提供能量。文献[1]指出某纯电动大巴在北京夏季工况下开启空调时循环工况续驶里程大大下降,可见,空调的使用对续驶里程产生的影响尤为显著;文献[2-3]指出在纯电动汽车匹配时要考虑到空调对续驶里程的影响。
电动汽车动力系统的合理匹配应保证动力传动系统既能满足电动汽车对于动力性和续驶里程的要求,同时又兼顾整车质量不至过重而使电池参数设计合理。文献[4]针对某纯电动轿车动力传动系统进行了优化匹配,并且验证了两挡变速器相对于固定挡变速器的优势所在,但未考虑电动空调等能耗附件对整车续驶里程等的影响。文章在考虑电动空调的使用对纯电动汽车动力性和续驶里程影响的基础上,对纯电动汽车动力传动系统进行了合理的参数匹配。考虑到在参数初选过程中对系统效率及换挡规律的简化,在传动系统部件确定后,根据各部件效率模型制定了基于动力传动系统综合效率最优的经济性换挡规律,并以循环工况能耗最小为目标对传动系速比进行了优化。
1 车型基本参数该电动汽车主要设计参数及性能要求如表 1所示。
| 表 1 车辆参数及设计要求 |
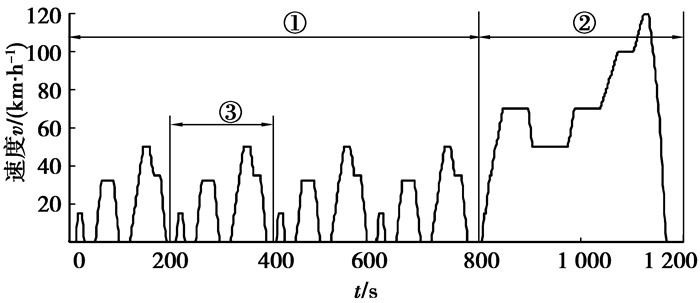
额定功率按汽车最常用的需求功率来确定。电动汽车能量消耗率和续驶里程试验方法GB/T 18386给出的循环工况如图 1所示,其中:①段为市区循环,由4个基本市区循环构成;②段为市郊循环。分析各个负荷功率段在整个循环工况中出现的频率如图 2所示,可见,超过16 kW的大功率需求在整个循环中出现频率比较小,而更多的功率需求处在中小功率段。因此,这里取各负荷功率段出现的频率作为其权值ai,加权求和后得到电机的额定功率,即PPe= aiMax(Pi)=10.56 kW。
|
图 1 GB/T 18386给出的循环工况 注:①市区循环;②市郊循环;③基本市区循环 |

|
图 2 市区循环功率特征分析 |
出现频率高的负荷在求和过程中贡献大,使额定功率能尽量靠近常用负荷,有利于经济性,而各个负荷功率段按其频率各有贡献,使设计的额定功率又能兼顾到循环工况中的平均动力性,最终取电机额定功率为11 kW。
2.2 电机其他参数及传动系速比的确定电机峰值功率关系到汽车的动力性能,而额定转速既对加速时间有显著影响,同时又是决定能耗经济性的一个重要指标。合理的速比匹配在一定程度上可降低动力性对电机性能的要求,同时,也可使电机较多地工作在额定工况点附近。为此,建立了如式(1)所示的目标函数,以动力性为约束条件对电机峰值转矩、额定转速、最高转速、传动系速比进行优选。由于该问题是多指标综合评价问题,所以目标函数中采用阈值法[5]对各指标进行无量纲化处理。
| $ \begin{array}{*{20}{c}} {{\rm{Min}}F\left( \mathit{\boldsymbol{X}} \right)}\\ {F\left( \mathit{\boldsymbol{X}} \right) = {a_1}{{\left[ {\frac{{\left( {{T_{\rm{m}}} - {T_{{\rm{m,min}}}}} \right)}}{{\left( {{T_{{\rm{m,max}}}} - {T_{{\rm{m,min}}}}} \right)}}} \right]}^2} + }\\ {{a_2}{{\left[ {\frac{{\left( {{n_{\rm{m}}} - {n_{{\rm{m,min}}}}} \right)}}{{\left( {{n_{{\rm{m,max}}}} - {n_{{\rm{m,min}}}}} \right)}}} \right]}^2} + {a_3}{{\left[ {\frac{{\left( {D - {D_{{\rm{min}}}}} \right)}}{{\left( {{D_{{\rm{max}}}} - {D_{{\rm{min}}}}} \right)}}} \right]}^2} + }\\ {{a_4}{{\left[ {\frac{{\left( {{i_{\rm{1}}} - {i_{{\rm{1,min}}}}} \right)}}{{\left( {{i_{{\rm{1,max}}}} - {i_{{\rm{1,min}}}}} \right)}}} \right]}^2} + {a_5}{{\left[ {\frac{{\left( {{i_{\rm{2}}} - {i_{{\rm{2,min}}}}} \right)}}{{\left( {{i_{{\rm{2,max}}}} - {i_{{\rm{2,min}}}}} \right)}}} \right]}^2},} \end{array} $ | (1) |
| $ \begin{array}{*{20}{c}} {D = \sum\limits_{i = 1}^n {{{\left[ {\frac{{\left( {{T_i} - {T_{\rm{N}}}} \right) - {\rm{Min}}\left( {{T_i} - {T_{\rm{N}}}} \right)}}{{{\rm{Max}}\left( {{T_i} - {T_{\rm{N}}}} \right) - {\rm{Min}}\left( {{T_i} - {T_{\rm{N}}}} \right)}}} \right]}^2}} + }\\ {{{\left[ {\frac{{\left( {{n_i} - {n_{\rm{N}}}} \right) - {\rm{Min}}\left( {{n_i} - {n_{\rm{N}}}} \right)}}{{{\rm{Max}}\left( {{n_i} - {n_{\rm{N}}}} \right) - {\rm{Min}}\left( {{n_i} - {n_{\rm{N}}}} \right)}}} \right]}^2},} \end{array} $ | (2) |
式中,n为循环工况负荷点个数。
约束条件G(X)≥0,
优化变量X=(Tm,nN,nm,i1,i2)T,X∈[A,B],
下限:A=(100,1 000,4 000,3,7)T,
上限:B=(200,4 000,10 000,7,15)T,
G(X)=[g1,g2,g3,g4,g5,g6,g7,g8],
式中各符号含义如表 2所示,D定义为每一循环工况点与额定工况点距离的平方,它在一定程度上反映了电机额定工况点和实际负荷点的差别。目标函数中每一项由因子ai进行加权,由于是初选,不必苛求结果,权值可全部选为1。笔者采用遗传算法进行优化[6-8],个体由Tm,nN,nm,i1,i2构成,采用二进制编码,约束条件通过惩罚函数法进行处理。参考5次计算结果中的最好点Xopt,初选电机、速比及对应的动力性如表 3所示。
| 表 2 式(1)、(2)符号释义表 |
| 表 3 驱动电机及变速器速比参数初选 |
电机额定电压与之前所选电机参数相关,同时又与电池组电压相关。在输出功率相同时,电池组电压高则电流小,对导线和开关等电器元件要求较低,但较高的电压需串联较多的单体电池,引起成本及整车质量增加和动力性下降且难于布置。参考大连电机集团已有电机系列,文章选用144VDC/75VAC(DC:直流,AC:交流)。
3 空调系统选型及建模 3.1 空调系统部件选型表 4给出了北京夏至日6:00—18:00的车室外热源参数[9],由此计算出的各时刻车室热负荷如表 5所示。在求得热负荷后,根据文献[10]给出的空调系统设计计算流程匹配空调部件参数如表 6所示。
| 表 4 北京夏季工况 |
| 表 5 车室热负荷计算值 |
| 表 6 空调参数 |
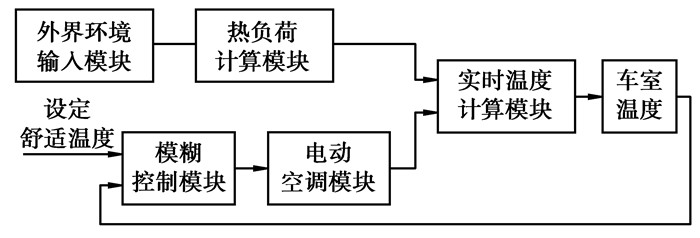
为准确计算空调系统实时功耗和能耗,从而对蓄电池进行匹配,建立了如图 3所示的Simulink空调系统模型[1]。给定外界热源、车室初始温度及驾驶员设定的舒适温度时,可计算出任意时刻空调系统的功率消耗、能耗以及车室实时温度。
|
图 3 电动汽车空调系统主模块 |
动力锂电池具有比能量高、比功率高的特点,适合应用在纯电动汽车上,因此,选择锂电池作为动力源。
电池电压等级应与电机电压等级相一致且满足电机电压变化的要求。由于存在电动空调等附件的功率消耗,所以电池组总电压须大于电机额定电压,从而有
| $ {U_{\rm{B}}} = {U_{\rm{m}}} + \frac{{\left( {{P_{\rm{m}}} + \Delta P} \right)R}}{{{U_{\rm{m}}}}} \approx 191\;{\rm{V}}, $ | (3) |
式中:UB为蓄电池电压;Um为电机额定电压;Pm为电机峰值功率;ΔP为附件功率;R为蓄电池内阻。附件功率可按所选空调电机额定功率的1.5倍取值,参考深圳沃玛100 Ah磷酸铁锂电池,内阻R取值为0.18 Ω,其产品系列中,单组电池电压有12 V、24 V、48 V等,因而总电压可选为192 V。
电池组容量为
| $ E = \frac{{{E_{{\rm{cyc}}}} + S}}{L}, $ | (4) |
| $ C = \frac{{1000E}}{{{U_{\rm{B}}}}}, $ | (5) |
式中:E为电池组携带的总能量;Ecyc为循环工况能耗;S为要求的续驶里程;L为循环工况的距离。为考察空调对整车性能的影响,在计算电池容量时分忽略空调能耗和加入空调能耗2种情况计算。
4.1.1 忽略空调能耗电池效率按0.9估算,建立Simulink逆向仿真模型,计算出循环工况下的经济性如表 7所示,由此初选电池参数:容量计算值C=68 Ah,参考深圳沃玛磷酸铁锂电池产品系列,可选为70 Ah,单组电池电压24 V,单组质量14 kg,总质量=14(kg/组)×8(组)=112 kg,更新整车质量重新计算整车动力性,其结果如表 7所示。
| 表 7 忽略空调能耗SOC=0.8时的经济性、动力性仿真结果 |
从表 7看出,开启空调时的续驶里程远不能满足设计要求。为此,按开启空调时的耗电量重新计算电池容量并参考已有产品系列,最终确定电池容量为120 Ah,总质量224 kg。
电池组质量增加必然导致动力性下降,如表 8所示,部分指标不能满足设计要求,因而须对电机参数及传动系速比做适当调整,调整后的电机参数、传动系速比及相应的动力性如表 9所示。
| 表 8 考虑空调能耗SOC=0.8时的经济性、动力性仿真结果 |
| 表 9 动力传动系统参数修正情况 |
电池组最大输出功率受其温度和SOC影响较大。考虑由电池组放电截止电压来限制其最大输出功率,有
| $ {P_{\max }} = \frac{{\left( {{V_{{\rm{oc}}}} - U} \right)U}}{R}, $ | (6) |
| $ U = {\rm{Max}}\left( {{U_{{\rm{ess}}\_\min }},{U_{{\rm{mc}}\_\min }},{V_{{\rm{oc}}}}/2} \right), $ | (7) |
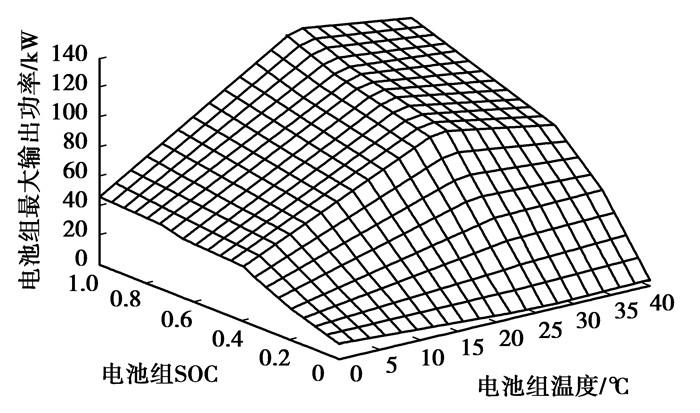
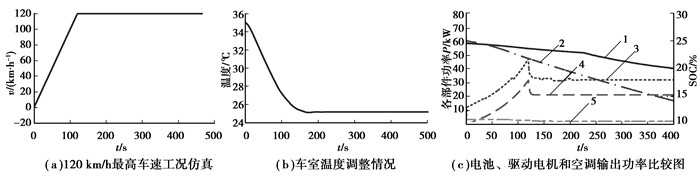
式中:Pmax是电池组最大输出功率;Umc_min为电机最低输入电压;Uess_min为电池组放电截止电压,二者取值分别由表 3及表 9所示。Voc、R为电池组开路电压和内阻,测得不同温度和SOC下电池组的开路电压和内阻后,得到对应的电池组最大输出功率,如图 4所示。为保证电池组在SOC设定范围内能够满足设计要求给出的任何功率需求,对电池组在4种极限工况下的功率输出能力进行验证,如图 5~图 8所示。仿真结果表明:在SOC接近0.2时,电池组最大输出功率约为52 kW,能够满足各种极限工况下的功率需求;而在几种工况中,最大需求功率也接近50 kW,如图 5所示的50~80 km/h加速工况,即接近SOC=0.2时的最大输出功率线。因此,在电池SOC下限取为0.2时,既能满足设计要求给出的任何功率需求,同时又没有过多的剩余功率,由此表明匹配合理。
|
图 4 蓄电池最大输出功率 注:1.电池组可输出最大功率;2.电池组SOC;3.电池组实际输出功率;4.主驱动电机实际输出功率;5.电动空调压缩机实际输出功率 |

|
图 5 50~80 km/h加速工况下电池组功率匹配情况(空调工况:从表 4中14:00开始仿真) |
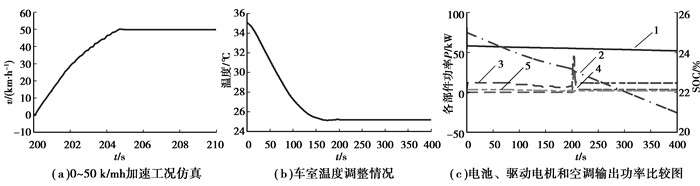
|
图 6 0~50 km/h加速工况下电池组功率匹配情况(曲线1~5含义同图 5) |
|
图 7 最高车速(120 km/h)下电池组功率匹配情况(曲线1~5含义同图 5) |
|
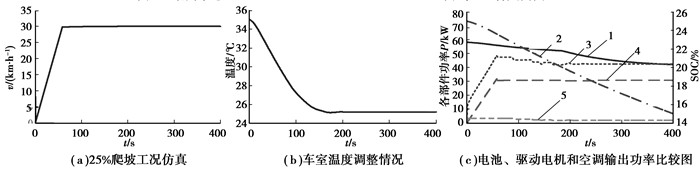
图 8 爬坡(25%)工况下电池组功率分配情况(曲线1~5含义同图 5) |
考虑到初选速比时各部件效率均以固定值替代,为保证整个传动系统高效运行,在各部件确定后,建立各自效率模型,并制定以车速和加速踏板开度为换挡参数,基于所选部件综合效率的经济性换挡规律。电池[11]、电机及变速器效率为
| $ {\eta _{{\rm{B,dis}}}} = \frac{{{V_{{\rm{Voc}}}} + \sqrt {V_{{\rm{Voc}}}^2 - 4RP} }}{{2{V_{{\rm{Voc}}}}}}, $ | (8) |
| $ {\eta _{{\rm{B,cha}}}} = \frac{{2{V_{{\rm{Voc}}}}}}{{{V_{{\rm{Voc}}}} + \sqrt {V_{{\rm{Voc}}}^2 - 4RP} }}, $ | (9) |
| $ {\eta _{\rm{m}}} = f\left( {T,n} \right), $ | (10) |
| $ {\eta _t} \approx 0.91, $ | (11) |
| $ \begin{array}{*{20}{c}} {{\eta _{{\rm{dis}}}} = {\eta _{{\rm{B,dis}}}}{\eta _{\rm{m}}}{\eta _t} = }\\ {0.91\left( {\frac{{{V_{{\rm{Voc}}}} + \sqrt {V_{{\rm{Voc}}}^2 - \frac{{4RTn}}{{9550f\left( {T,n} \right)}}} }}{{2{V_{{\rm{Voc}}}}}}} \right)f\left( {T,n} \right)。} \end{array} $ | (12) |
在上述有关各式中,蓄电池采用开路电压内阻模型,其效率如式(8)、(9),其中,VVoc、R、P、ηB,dis、ηB,cha分别是电池开路电压、内阻、输出功率、放电和充电效率。电机稳态效率[12]是关于输出扭矩和转速的函数,如式(10),其中,ηm为电机效率,T、n分别为电机扭矩和转速。变速器效率大致在90%~92%[13],考虑到该变速器挡位少且变化范围不大,其效率ηt采用固定值0.91。于是,放电时某一负荷点(T,n)对应的系统效率如式(12),充电时的系统效率只需将电池放电效率换成充电效率即可。式中VVoc、R会随电池温度和SOC的变化而变化,但经验证,其对换挡规律的影响很小,可忽略。
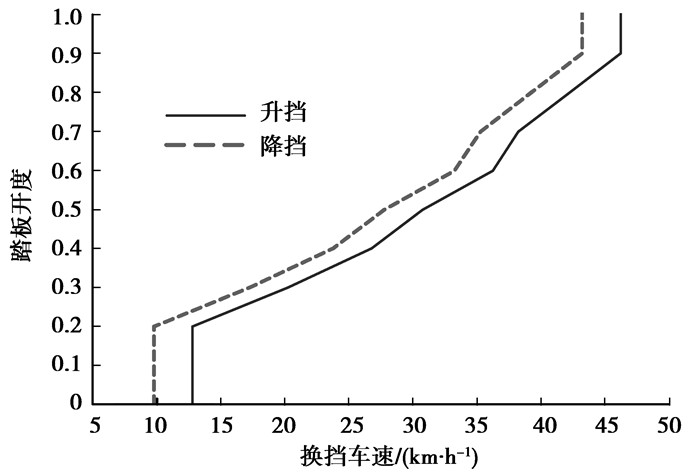
确定换挡曲线时,取每一踏板开度下两挡效率曲线的交点作为该开度下的升挡车速,如果没有交点则取低挡效率曲线的末端车速为升挡车速。降挡车速则在其基础上做一延迟以避免循环换挡,如图 9所示。
|
图 9 经济性换挡曲线 |
以循环工况能耗最小为目标对初选速比进行优化[14-16],结果如表 10所示,可见,开启空调时续驶里程可延长4.29%,关闭空调时可延长5.28%。
| 表 10 修正前后结果对比 |
1) 重点考虑了电动空调作为能耗附件对整车续驶里程的影响,并在此基础上对蓄电池、驱动电机和变速器参数进行了匹配设计。
2) 所匹配的蓄电池既满足了汽车动力性和续驶里程要求,同时又保证了开启空调时的续驶里程不超过设计要求的10%,从而确保整车质量不至过重,即权衡了整车轻量化与整车对于动力性、续驶里程要求之间的矛盾。
3) 初选基础上的速比优化使得续驶里程在空调关闭时提高了5.28%,空调开启时提高了4.29%。
| [1] |
闵海涛, 曹云波, 曾小华, 等.
电动汽车空调系统建及对整车性能的影响[J]. 吉林大学学报:工学版, 2009, 39(Sup1): 53–57.
MIN Haitao, CAO Yunbo, ZENG Xiaohua, et al. Modeling of air conditioning system for electric vehicles and its effects to vehicles performance[J]. Journal of Jilin University:Engineering and Technology Edition, 2009, 39(Sup1): 53–57. (in Chinese) |
| [2] | Park S J, Jung D. Design of vehicle cooling system architecture for a heavy duty series hybrid electric vehicle using numerical system simulations[J]. Journal of Engineering for Gas Turbines and Power, 2010, 132(9). |
| [3] |
曹中义.
电动汽车空调系统解决方案[J]. 汽车电器, 2008(3): 1–4.
CAO Zhongyi. Solution to air conditioning on EVs[J]. Auto Electric Parts, 2008(3): 1–4. (in Chinese) |
| [4] |
秦大同, 周保华, 胡明辉, 等.
两挡电动汽车动力传动系统的参数设计[J]. 重庆大学学报, 2011, 34(1): 1–6.
QIN Datong, ZHOU Baohua, HU Minghui, et al. Parameters design of powertrain system of electric vehicle with two-speed gearbox[J]. Journal of Chongqing University, 2011, 34(1): 1–6. (in Chinese) |
| [5] |
朱正礼, 殷承良, 张建武.
基于遗传算法的纯电动轿车动力总成参数优化[J]. 上海交通大学学报, 2004, 38(11): 1907–1912.
ZHU Zhengli, YIN Chengliang, ZHANG Jianwu. Genetic algorithm based optimization of electric vehicle powertrain parameters[J]. Journal of Shanghai Jiaotong University, 2004, 38(11): 1907–1912. DOI:10.3321/j.issn:1006-2467.2004.11.030 (in Chinese) |
| [6] | Cabral H A, Melo M T. Using genetic algorithms for device modeling[J]. IEEE Transactions on Magnetics, 2011, 47(5): 1322–1325. DOI:10.1109/TMAG.2010.2099107 |
| [7] | Cho J R, Lee J H, Jeong K M, et al. Optimum design of run-flat tire insert rubber by genetic algorithm[J]. Finite Elements In Analysis and Design, 2012, 52: 60–70. DOI:10.1016/j.finel.2011.12.006 |
| [8] | Heo J H, Kim M K. A Reliability-centered approach to an optimal maintenance strategy in transmission systems using a genetic algorithm[J]. IEEE Transactions on Power Delivery, 2011, 26(4): 2171–2179. DOI:10.1109/TPWRD.2011.2162752 |
| [9] | 王晓丹. 纯电动客车空调系统参数匹配与设计研究[D]. 长春: 吉林大学硕士学位论文, 2009. |
| [10] |
闵海涛, 王晓丹, 曾小华, 等.
电动汽车空调系统参数匹配与计算研究[J]. 汽车技术, 2009(6): 19–23.
MIN Haitao, WANG Xiaoxian, Zeng Xiaohua. Parameter design and computation study for air conditioning system of electric vehicle[J]. Automobile Technology, 2009(6): 19–23. (in Chinese) |
| [11] | 胡明辉. CVT轻度混合动力汽车能量管理策略研究[D]. 重庆: 重庆大学硕士学位论文, 2007. |
| [12] | Xiaofeng D, Chris M. Modeling of eddy current loss and temperature of rhe magnets in permanent magnet machines[J]. Journal of Circuits Systems and Computers, 2011, 20(70): 1287–1301. |
| [13] |
王熙, 秦大同, 胡明辉, 等.
汽车变速器传动效率理论建模与实验测试[J]. 机械传动, 2010, 34(8): 21–24.
WANG Xi, QIN Datong, HU Minghui, et al. Modeling and testing of the vehicle transmission efficiency[J]. Journal of mechanical transmission, 2010, 34(8): 21–24. (in Chinese) |
| [14] | He R, Wang J F. Interval optimization of automobile transmission parameters.SAE, 1999-01-0733. |
| [15] | Delphine S, Gregory R, Yohan M. Design optimization and optimal control for hybrid vehicles[J]. Optimization and Engineering, 2011, 12(1): 199–213. |
| [16] | Van B K, Hofman T, Vroemen B, et al. Optimal control of a mechanical hybrid powertrain[J]. IEEE Transactions on Vehicular Technology, 2012, 61(2): 485–497. DOI:10.1109/TVT.2011.2178869 |
 2013, Vol. 36
2013, Vol. 36

