b. 重庆大学 研究生创新实践基地, 重庆 400044
b. Graduate Innovation Base, Chongqing University, Chongqing 400044, China
在众多应力应变测量工具中,电阻应变式传感器以其较高的测量精度和稳定性至今仍是应用最广泛的测量工具之一[1]。实践表明,电阻应变式传感器应变片各组成元件的结构参数在一定程度上影响应变片的测量性能,尤其是敏感栅的结构参数在很大程度上影响着测量的系统误差。在这方面,研究人员已经做了大量的工作:李鹏等[2]研究了应变片的横向效应对应变片测量结果的影响;庄重等[3]对应变测试中横向效应引起的误差进行了分析;日本大井、小岛及美国Larry Burrow等[4-5],先后用有限元方法分析了应变片结构与其各项性能的关系;尹福严[6]研究了应变片的应变传递机理及端部效应和胶层蠕变现象对应变传递灵敏度的影响,并进行了结构有限元分析;孟凡文[7]研究了通过提高线性度、灵敏度和减小温度误差方面的作用来提高应变式传感器测量性能的几种方法;Wie Fuyu等[8]使用有限元仿真技术分析了高精度传感器输出非线性误差的影响因素并计算了误差值,得出了测量区域应变梯度是输出中非线性误差的主要影响因素的结论;Ahmed A. S.等[9]研究了一种新型微电子机械应变传感器的发展并对其进行了实验评价;J.P.Wang等[10]利用电阻应变式传感器原理研究了导电光纤在测量中的应变传递状况;Yin-Nee Cheung等[11]对一种可以测量大变形的流变应变传感器测量精度进行了研究;N.M.Khairi等[12]通过选择不同栅长的应变片测量植物杆径的变化,以此来判断何时适合灌溉,并得到了2 mm应变片在此次测试中能够得出更真实结果的结论。
以上文献表明:目前国内外对电阻应变式传感器的研究主要集中在两方面:横向效应、端部效应以及长导线因素等对测量误差的影响;利用电阻应变式传感器基本原理的新型传感器的测量精度分析。研究方法主要是基于简化的数学模型,应用有限元方法对敏感栅结构参数在基体应变传递误差中的影响的系统研究还很少,而栅丝间距改变时误差的变动情况以及栅丝长度和栅丝直径对基体应变传递误差影响的研究则未见报道,这使得工程测量中对应变片的选择存在一定的盲目性。为此,建立了一个由悬臂梁(被测基体)、粘结剂和应变电阻丝所组成的悬臂梁测量模型,运用有限元方法对应变传递误差变动规律及大小进行分析,为测量过程中电阻应变式传感器结构参数的选择和进行适当的误差补偿提供了有效参考。
1 电阻应变片结构及其测量原理电阻应变片是利用敏感栅电阻丝的应变电阻效应研制而成的,其基本原理是:当被测对象受力变形时,应变片的敏感栅也随同变形,其电阻值发生相应变化,通过转换电路转换为电压或电流变化以供检测。
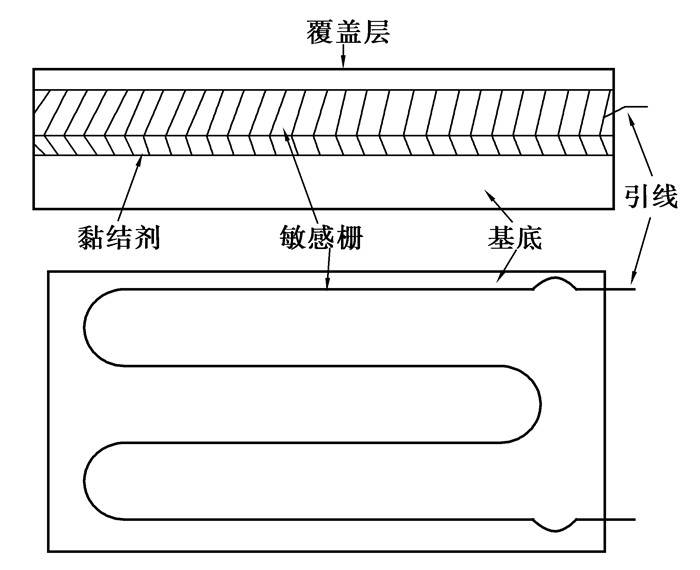
1.1 电阻应变片结构丝式电阻应变片主要由基底、敏感栅和覆盖层等组成,其结构如图 1所示。
|
图 1 金属丝式应变片的典型结构 |
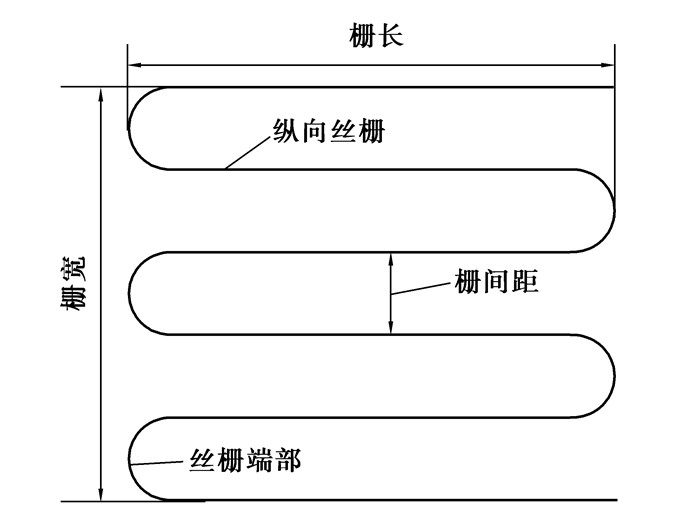
图 1中,敏感栅一般由直径为0.015~0.05 mm的金属丝绕制而成,它是应变片的转换元件,实现应变—电阻的转换,其材料采用铜镍合金(俗称康铜)。基底是由绝缘材料制成,敏感栅用粘合剂粘贴在基底上,并在敏感栅上粘贴有保护作用的覆盖层,引线是敏感栅与测量电路的连接线。为准确传递试件上的应变,基底必须很薄,一般为0.03~0.06 mm,材料为纸、胶膜、浸胶玻璃纤维等。覆盖层一般为纸或胶。其中敏感栅的详细结构组成及各部分名称如图 2所示,栅长×栅宽称为应变片使用面积[13-14]。
|
图 2 丝式应变片敏感栅的结构组成 |
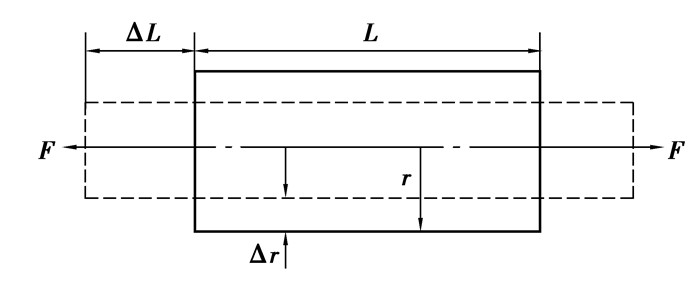
敏感栅金属丝在外力作用下发生机械变形时,其电阻值将发生变化。如图 3所示,一根金属电阻丝,在其未受力时,原始电阻值为
|
图 3 金属丝的电阻应变效应 |
| $ R = \rho \frac{L}{S}, $ | (1) |
式中:ρ为电阻丝的电阻率;L为电阻丝的原始长度;S为电阻丝的原始横截面积。
当敏感栅受到拉力F作用时,将伸长ΔL,横截面积相应减小ΔS,电阻率也因晶格发生变形等因素的影响而改变Δρ,故引起阻值变化ΔR。当应变片随被测体变形时,电阻丝应变就是基体应变,其电阻的变化率与基体应变ε的关系为
| $ \frac{{\Delta R}}{R} = {S_n}\varepsilon 。$ | (2) |
式(2)为应变片工作原理表达式,应变ε就是所测得的被测体(试件)的应变,Sn为应变片的灵敏系数。
根据式(2)可得到被测基体的应变值ε,已知被测体的弹性模量,由应力应变公式
| $ \sigma = {E_\varepsilon }, $ | (3) |
即可得到被测基体测量区域的应力值,此处没有考虑应变传递误差。
2 有限元模型的建立及其验证为详细了解敏感栅的不同结构参数对测量结果的影响规律及大小,建立了含应变片敏感栅、粘结剂以及被测基体的悬臂梁有限元测量模型。首先对模型中基体的应力及挠度进行理论验证,证明在悬臂梁有限元模型中加入粘结剂和敏感栅后基体的应力和挠度依然符合理论结果;然后对有限元测量模型中应变传递误差进行分析并进行相关的实验验证。
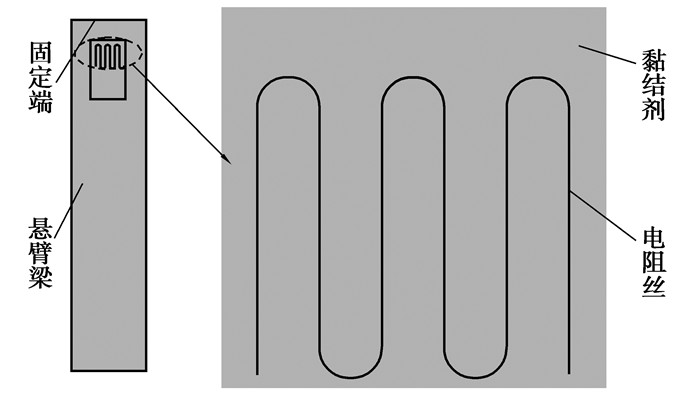
2.1 有限元测量模型的建立与理论验证建立一个由悬臂梁(即被测基体)、粘结剂和敏感栅电阻丝所组成的测量模型,如图 4所示。悬臂梁为50 mm×10 mm×10 mm的等截面梁,材料采用Q235。
|
图 4 悬臂梁模型 |
若悬臂梁固定端另一侧施加600 N向下的载荷,则由理论知识可知悬臂梁固定端处最大应力为[13, 15]
| $ {\delta _{\max }} = \frac{{6FL}}{{bh^2}} = \frac{{6 \times 600 \times 50}}{{10 \times {{10}^2}}}{\rm{ = }}180\;{\rm{MPa, }} $ |
自由端处的最大挠度为
| $ {\mathit{y}_{\max }} = \frac{{4F{l^3}}}{{b{h^3}E}} = 0.15\;{\rm{mm}} $ |
图 5和图 6为有限元计算结果云图。由图可知,悬臂梁固定端最大应力值177.1 MPa,与理论值误差为1.6%;自由端处挠度为0.154 mm,与理论值误差为2.7%。说明仿真结果与理论计算基本一致;有限元测量模型中粘结剂和敏感栅的添加对测量基体的应变和自由端的挠度没有影响,所建模型可做进一步的验证分析。
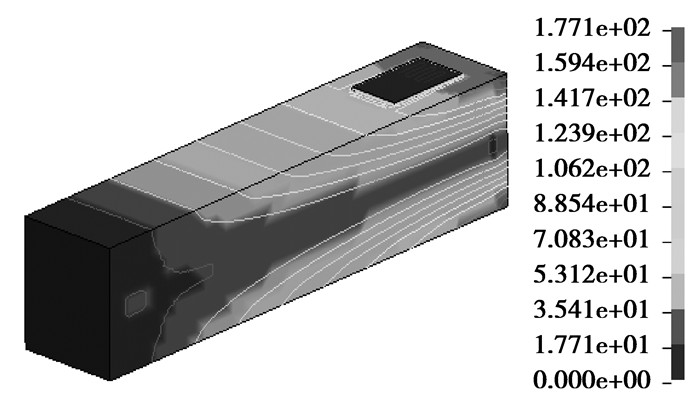
|
图 5 悬臂梁应力分布云图(Mpa) |

|
图 6 悬臂梁挠度分布云图(mm) |
由测量原理可知,应变片在测试过程中的误差有很大一部分是由基体应变到敏感栅的传递误差引起的,分析并验证有限元测量模型中这一传递误差的大小能够进一步证明整个有限元测量模型的有效性。图 7和图 8分别为被测基体和应变电阻丝的应变分布云图。

|
图 7 悬臂梁应变分布云图 |
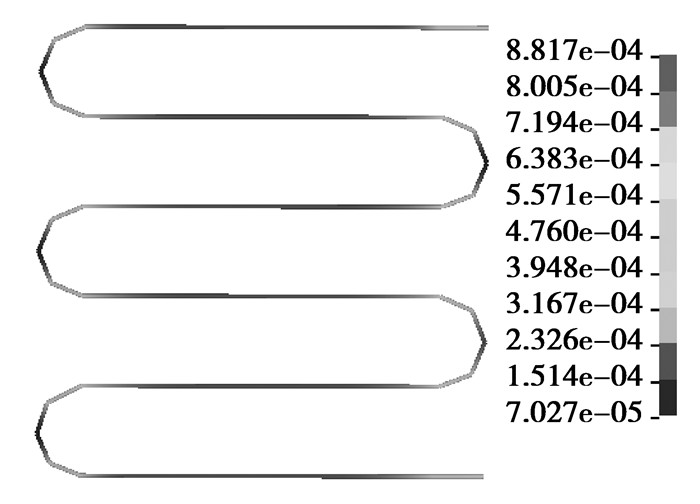
|
图 8 电阻丝应变分布云图 |
可以看出,悬臂梁被测位置范围内的应变有所不同,敏感栅电阻丝每个位置处的应变也有所不同。研究中取测量面积内基体上表面一层单元的平均应变作为基体的应变如图 9所示;电阻丝输出应变则由ε=dL/L获取,L为电阻丝的总长。为了对比两者的差异,分别计算悬臂梁由低应变到高应变状态时悬臂梁被测位置的应变和应变片的输出应变,结果如表 1所示。
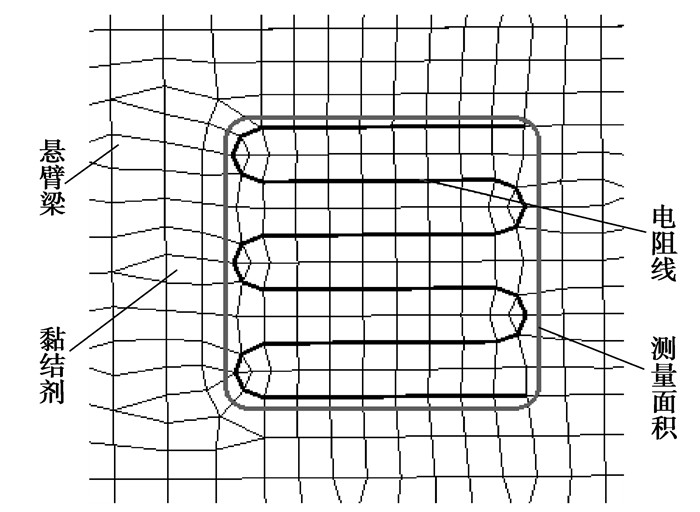
|
图 9 基体被测应变的读取范围 |
| 表 1 不同应变状态下悬臂梁模型的计算结果 |
由表 1可看出,电阻丝的输出应变与基体被测应变误差基本保持在5.6%左右,该模型电阻丝应变输出误差较稳定,即测量情况稳定,且误差较小,说明该模型中所建立的应变片基本可以反应悬臂梁的应变变形情况,即说明了该应变测量的有限元模型是准确的,同时也反映了电阻应变式传感器精确测量的弊端—应变传递始终存在误差。当然,对于稳定误差可以通过传感器的标定进行弥补[16]。
为验证以上测量模型应变传递误差的分析结果,根据测试原理搭建了应变测试系统,被测模型与有限元分析的测量模型一致,测量不同作用力下悬臂梁的应变并对照有限元结果以检验有限元测量模型中的应变传递误差。由于需测量多组实验数据,实验持续时间较长,温度影响不可忽略,因此实验采用带温度补偿的半桥电路,采集卡为NI-9237应变模块,测试系统如图 10所示。

|
图 10 应变测试系统 |
对测量结果进行数据处理,所得结果如表 2所示。
| 表 2 悬臂梁应变有限元计算与测试结果对比 |
由表 2数据可以看出不同载荷下基体应变测试结果与有限元计算结果的误差基本稳定在9%~10%,表明有限元分析满足精度要求。
综上,通过测量模型基体应变的理论验证、应变片应变传递误差的分析以及有限元计算与实验对比证明了本文所建立有限元测量模型是有效的,可以应用到接下来的研究中。
3 敏感栅结构参数对测量的影响由图 2知,敏感栅由电阻丝绕制而成,包括纵向丝栅,丝栅端部(横栅)。其结构基本参数为栅长、栅丝间距和栅丝直径。在此,基于有限元分析重点研究了这3个参数对测量精度的影响规律及大小,并通过实验对敏感栅长度变化对测量结果的影响进行了实验验证。
3.1 敏感栅栅长变化对测量结果的影响及其实验验证敏感栅栅宽一定时,栅长决定了应变片的测量面积。为此计算了栅长为2.0~5.0 mm时,应变片的输出应变及其与基体应变的误差大小,如表 3所示。计算中,保持每个模型的栅丝间距和直径不变,并且基体处于同一应变状态。对于不同的栅长模型,应变片的测量面积沿主应变方向变化。
| 表 3 不同栅长的电阻丝模型计算结果 |
由表 3数据可看出,基体同等应变状态下,栅长从2 mm增大到4 mm时,电阻丝的输出应变与基体被测应变之间的误差从13.5%降低到0.51%,而栅长增长5 mm时,误差又增大到5.60%。说明在被测基体应变梯度一定的前提下,应变片栅长具有中间最优值,栅长过长或过短都将增加应变传递误差。栅长过长覆盖的应变范围太大误差增大,栅长过短横向效应影响增大误差也将增加。因此测量中针对特定的被测基体应变片栅长具有最优值,栅长选择是否合适将直接影响测量误差。
基于以上分析,应用应变测试系统进行不同栅长应变片对测量精度的影响进行分析。试验中在测量模型相同位置粘贴不同栅长的应变片并施加相同载荷进行分析,测得结果统计分析如表 3所示。
由表 4可以看出测量模型在相同载荷下栅长从1 mm增大到4 mm时,应变传递测量误差减小,而当敏感栅长度达到5 mm时误差稍有增加,表明4 mm栅长敏感栅在该被测基体应变测量中可以获得最好的结果,该结论与表 3中的数据分析结论相吻合,表明敏感栅栅长对于测量误差具有中间最优值。
| 表 4 不同栅长应变片悬臂梁模型测试结果 |
由于应变片的敏感栅存在横向效应,圆弧栅的直径大小直接关系到横向效应的大小,而圆弧栅的直径等于敏感栅的栅丝间距,所以敏感栅丝间距过大时横向效应影响增大误差增大。而栅间距过小时,同等栅宽下电阻丝长度过长,灵敏度系数减小从而使测量不准确。因此,敏感栅栅丝间距也应具有中间最优值。
查阅相关资料显示:弧形栅的半径r的范围为0.1~0.3 mm,所以栅丝间距的范围为0.2~0.6 mm。表 5计算了栅间距为0.1~0.6 mm范围内应变片的输出应变及其与基体被测应变的误差大小。计算中,保持每个模型的栅长和栅丝直径不变,且基体处于同一应变状态下。
| 表 5 不同栅间距的电阻丝模型计算结果 |
由表 5数据可看出,基体同等应力应变状态下,栅间距从0.6 mm减小到0.3 mm时,电阻丝的输出应变与基体应变之间的误差从5.20%减小到0.22%,而栅间距减小到0.1 mm时,误差又增大到6.84%。说明一定应变范围内,栅间距越小,应变片测量误差越小,但栅间距并不是越小越好,它有其最优值,正好与前面的分析相吻合。
实际上,一定范围内应变片的栅间距减小,而栅长不变,同样相当于增大了纵栅的栅长,该仿真结果也与敏感栅长的仿真结果相吻合。
3.3 敏感栅栅丝直径变化对测量结果的影响查阅文献可知,敏感栅栅丝直径越小越容易传递基体产生的应变,测量结果就能更准确反映被测基体应变,但受生产工艺及可靠性限制,栅丝直径不可能做的太细,常用的敏感栅栅丝直径范围为0.015~0.05 mm。笔者分别计算了栅丝直径为0.015 mm、0.02 mm、0.03 mm、0.04 mm、0.05 mm时应变片的输出与基体应变的误差大小,结果如表 6所示。计算中,保持每个模型的栅长和栅丝间距不变并且基体处于同一应变状态下。
| 表 6 不同栅丝直径的电阻丝模型计算结果 |
由表 6数据可看出,基体同等应力应变状态下,栅丝直径由0.015 mm增大到0.05 mm时,电阻丝的输出应变与基体被测应变之间的误差从2.73%增大到11.76%。说明栅丝直径越小,应变片测量误差越小,即电阻丝越细,越容易反映被测基体的变形。但栅丝越细对生产工艺要求越高,成本也就越高,所以传感器的选择应综合考虑所有因素。
4 结论1) 通过有限元和实验验证所建立的有限元测量模型可以正确反应被测基体的应变变形。有限元计算的敏感栅电阻丝结构参数对应变传递误差的影响规律与定性分析一致,并且对敏感栅栅长变化对应变传递误差的影响进行了实验验证,表明在传感器应变传递误差分析中有限元方法是有效可行的。
2) 敏感栅电阻丝结构参数栅长和栅间距对应变传递误差具有中间最优值,而栅丝直径越细基体应变传递误差越小,因此传感器选择中应综合考虑各因素的影响以使应变传递误差达到最小值。
3) 研究给出了敏感栅各结构参数对应的相对误差大小,为测量过程中电阻应变式传感器结构参数的选择和进行适当的误差补偿提供了有效参考。
| [1] | Stefǎnescu D M, Anghel M A. Electrical methods for force measurement-A brief survey[J]. Measurement, 2013, 46(2): 949–959. DOI:10.1016/j.measurement.2012.10.020 |
| [2] |
李鹏, 黄晴.
测量中应变片的误差分析[J]. 企业家天地, 2008(6): 262–263.
LI Peng, HUANG Qing. Measurement error analysis of strain gauge[J]. Enterpriser World, 2008(6): 262–263. (in Chinese) |
| [3] |
庄重, 张娜.
电阻应变测试中横向效应误差分析[J]. 科技传播, 2010(21): 160–169.
ZHUANG Zhong, ZHANG Na. Resistance strain measurement error analysis of transverse effect[J]. Public Communication of Science & technology, 2010(21): 160–169. (in Chinese) |
| [4] | Stein P K. Strain gage history and the end of the twentieth century[J]. Experimental Techniques, 2001, 25(2): 15–16. DOI:10.1111/ext.2001.25.issue-2 |
| [5] | Larry B. Applying finite element analysis methods to strain gage design[EB/OL].[2013-01-15].http://loadcelltheory.com/LoadCelluSupportTheoryPDF/FEA-StrainGageDesign.pdf |
| [6] |
尹福炎.
箔式应变片结构模型与有限元分析[J]. 衡器, 2009, 38(6): 47–52.
YIN Fuyan. Foil strain gauge structure model and finite element analysis[J]. Weighing Apparatus, 2009, 38(6): 47–52. (in Chinese) |
| [7] |
孟凡文.
提高应变式传感器性能的几种方法[J]. 中国仪器与仪表, 2003(4): 34–37.
MENG Fanwei. Some ways to improve the property of strain sensor[J]. China Instrumentation, 2003(4): 34–37. (in Chinese) |
| [8] | Wie F Y, Fang M N. Factors influencing output non-linearity error of a high-precision load sensor and the error calculation[J]. Finite Elements in Analysis and Design, 2001, 37(4): 341–347. DOI:10.1016/S0168-874X(00)00047-0 |
| [9] | Mohammed A A S, Moussa W A, Lou E. Development and experimental Evaluation of a novel piezoresistive MEMS strain sensor[J]. IEEE Sensors Journal, 2011, 11(10): 2220–2232. DOI:10.1109/JSEN.2011.2113374 |
| [10] | Wang J P, P X, Tao X M. Strain sensing behavior of electrically conductive fibers under large deformation[J]. Materials Science and Engineering:A, 2011, 528(6): 2863–2869. DOI:10.1016/j.msea.2010.12.057 |
| [11] | Cheung Y N, Yun Z, Cheng C H, et al. A novel fluidic strain sensor for large strain measurement[J]. Sensors and Actuators A:Physical, 2008, 147(2): 401–408. DOI:10.1016/j.sna.2008.05.013 |
| [12] | Khairi N M, Shoh Rizam M S B, Naimah M I, et al. Diameter stem changes detection sensor evaluation using different size[J]. Procedia Engineering, 2012, 41: 1421–1425. DOI:10.1016/j.proeng.2012.07.330 |
| [13] | 单成祥, 牛彦文, 张春. 传感器原理与应用[M]. 北京: 国防工业出版社, 2006. |
| [14] | 施湧潮, 梁福平, 牛春晖. 传感器检测技术[M]. 北京: 国防工业出版社, 2007. |
| [15] | 卢兴国. 微型多功能传感器的研制[D]. 合肥: 合肥工业大学硕士学位论文, 2005. http: //cdmd. cnki. com. cn/Article/CDMD-10359-2006013044. htm |
| [16] |
吴强, 俞志伟, 吉爱红, 等.
一种小型电阻应变式三维力传感器的仿真设计[J]. 中国机械工程, 2011, 22(11): 1288–1293.
WU Qiang, YU Zhiwen, JI Aihong, et al. Development of a miniature resistance strain three dimensional force densor[J]. China Mechanical Engineering, 2011, 22(11): 1288–1293. (in Chinese) |
 2013, Vol. 36
2013, Vol. 36

