在低压配电系统中多采用分散的小功率用电设备,如紧凑型荧光灯(compact fluorescent lamp,CFL)、液晶显示器(liquid crystal display,LCD)、计算机、笔记本电脑、液晶电视、电子整流荧光灯、变频空调、洗衣机、冰箱等。这些设备广泛而随机地分布在低压配电系统中,构成了典型的分布式谐波源。虽然单个设备的功率小,但其电流畸变率大,有些甚至超过100%,大量此类非线性负荷产生的谐波电流注入到系统,将引起严重的电压畸变,不利于系统的稳定和经济运行,同时降低了设备的工作效率和使用寿命。为了对系统中的谐波进行有效的分析、评估和治理,需要有合理的模型来表征此类谐波源的特性,以便进行谐波水平评估和谐波潮流分析。
近年来,许多学者展开了该类谐波源模型的研究并取得大量的成果[1-12]。其中恒流源模型是最简单也是使用最广泛的谐波源模型[1-2],但该模型并不能准确反映谐波电压与谐波电流之间的耦合关系以及由此产生的谐波衰减效应和谐波分散效应[3-4]。
文献[5-7]提出了谐波耦合导纳矩阵模型,其模型精确,能很好地反映负荷的谐波电流特性,并能体现输入端电压与负载谐波电流之间的交互作用及电压畸变引起的电流衰减效应。但该模型需要对谐波耦合导纳矩阵中的元素进行迭代求取,不仅计算量大,且要求已知负载内部的电路参数。此外,还有基于传递矩阵的谐波源模型[8]及基于最小二乘逼近的谐波源模型[9]等。这些模型都因为存在参数求取困难的问题,其应用受到一定程度的限制。
在低压配电系统中,谐波源负荷存在数量大、分散性强的特点,迫切需要能反映其主要特征的简单模型进行表述。有学者提出了一种简单的谐波模型—谐波Norton模型[10-12],它的优势在于不需要已知负荷的电路参数,通过波动量法[13]即可获取模型参数。谐波Norton模型结构简单,不仅可以很方便地用于谐波潮流分析,还可以用于谐波源识别[14-16],即通过在公共耦合点(point of common coupling,PCC)处将负荷等效成一个谐波电流源与一个谐波阻抗相并联的Norton模型,依据测量参数得到的Norton模型进行谐波源对PCC处谐波贡献的评估。
严格意义上讲,采用波动量法获得Norton模型的方法仅对线性负荷(恒阻抗和恒功率负荷)和理想电流源(恒流源负荷)适用,对于含有大量分布式谐波源的低压系统,能否以Norton模型表述其集中谐波特性还有待研究。在文献[17]中,作者通过实验阐述了低压系统中单相非线性负荷使用Norton模型会出现参数不稳定的情况,对低压系统负荷能否用Norton模型进行等效提出了质疑,但未做更深入的分析研究,未给出不同电压条件下,Norton模型参数不稳定的原因,也未提供模型成立的适应条件及适应范围。在文献[18-19]中,作者采用“干预式”法(电容投切的方法)不仅能获得系统侧的Norton模型参数,而且能获取负荷侧的Norton模型参数,并将获得的参数进行谐波贡献的评估。但是负荷侧参数相对于系统侧参数而言,更具分散性,利用分散性的负荷侧参数进行谐波贡献水平的评估,其可靠性及准确性都是个值得研究的问题。
主要利用实验和仿真结果,分析和研究了低压配电系统中的单相非线性负荷用Norton模型简化表示的可行性及其成立条件,以及不同运行条件或方法获得的Norton模型的一致性及其对模型应用产生的影响。
1 负荷Norton模型负荷侧的Norton模型是将负荷的某次谐波电流特性通过并联的等效阻抗和电流源来体现,如图 1所示。
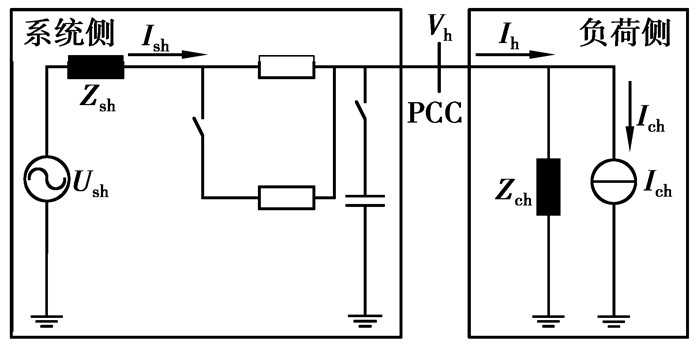
|
图 1 负荷侧的诺顿模型和系统侧的戴维南等效电路 |
对于阻抗和电流源均恒定的电路来说,可以通过波动量法获得h次谐波的模型参数,即通过测量变化的2次谐波电压(Vh(1)、Vh(2))与其对应的谐波电流(Ih(1)、Ih(2))的计算获取,其表达式为
| $ {Z_{{\rm{ch}}}} = \frac{{V_{\rm{h}}^{\left( 2 \right)}-V_{\rm{h}}^{\left( 1 \right)}}}{{I_{\rm{h}}^{\left( 2 \right)}-I_{\rm{h}}^{\left( 1 \right)}}}, $ | (1) |
| $ {I_{{\rm{ch}}}} = I_{\rm{h}}^{\left( 1 \right)}-\frac{{V_{\rm{h}}^{\left( 1 \right)}}}{{{Z_{{\rm{ch}}}}}} = I_{\rm{h}}^{\left( 2 \right)}-\frac{{V_{\rm{h}}^{\left( 2 \right)}}}{{{Z_{{\rm{ch}}}}}}, $ | (2) |
式中:Vh(1)和Ih(1)表示前一次测量值;Vh(2)和Ih(2)表示后一次测量值;Ich与ZchZch分别表示谐波电流源与谐波阻抗。需特别注意的是:2次测量中基波电压的相角必须保持一致(实际测量中基波电压相角很难保持一致,通常将基波电压相角变为0°,将其他次谐波相位相对于基波相角进行转化),并且2次谐波电压的变化不能太小,否则与之对应的2次谐波电流的变化也将很小,导致式(1)中存在减法误差,从而导致计算的参数不精确[17]。
若选择标准余弦电压作为波动量法中变化前的电压,由于不含谐波,即Vh(1)=0,式(1)~(2)可简化为
| $ {I_{{\rm{ch}}}} = I_{\rm{h}}^{\left( 1 \right)}, $ | (3) |
| $ {Z_{{\rm{ch}}}} = \frac{{V_{\rm{h}}^{\left( 2 \right)}}}{{I_{\rm{h}}^{\left( 2 \right)}-{I_{{\rm{ch}}}}}}。$ | (4) |
因此,若选择标准余弦电压作为波动量法中变化前的电压,模型参数Ich是恒定不变的,若其值发生较大偏差,显然是由式(1)中减法误差所致。
为计算负荷侧的Norton模型参数,需要系统提供2种不同的运行条件,不同的运行条件将直接体现了PCC处各次谐波电压的变化。运行条件的改变可以通过多种方式,比如投切电容器、并联运行一台变压器、并联阻抗或其他一些方法,从而导致供电系统的谐波阻抗发生显著变化[11],最终体现在PCC处谐波电压的变化上。实现这些方法通常会对系统带来一定的干扰,影响系统的正常运行,这些方法被称为“干预式”法。“非干预式”法则利用系统自身的谐波源以及可观测参数等实现PCC处谐波电压的变化。无论采用“干预式”法还是“非干预式”法,最终都将导致PCC处的电压及电压引起电流发生波动,波动量法正是利用PCC处电压和电流的波动量,获取负荷的Norton模型参数。对于低压系统中单相非线性负荷而言,谐波电流的波动量与谐波电压的波动量并不呈现线性关系,模型参数依赖于波动量,这使Norton模型的准确性存在争议[17]。
2 低压配电系统电压特征分析实验室实测的电压波形与对应标准余弦波的波形示意图如图 2所示。
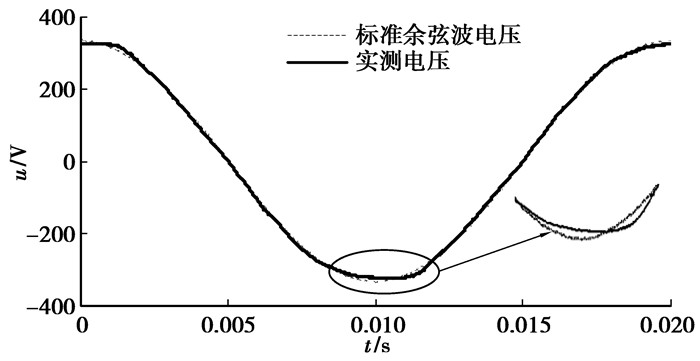
|
图 2 2种电压波形示意图 |
从图 2中不难看出:实测的电压波形的顶部呈现出平坦特征。这种顶部平坦波形将导致接入系统中的负荷发生谐波衰减效应[20]。为了描述低压系统电压波形的顶部特征,引用波峰系数(crest factor,CF)来表征
| $ {\rm{CF}} = \frac{{{V_{\max }}}}{{{V_{{\rm{rms}}}}}}, $ | (5) |
式中:CF为电压波峰系数;Vmax为输入电压的峰值;Vrms为输入电压的有效值。因此,标准余弦电压的波峰系数为
为了进一步验证低压配电系统电压表现为平坦波波形,在低压系统某负荷(CFL和LCD)的接入点处采集多组数据(中午12 : 00到第二天中午12 : 00,每次测量间隔为1 min,共获得1 440组数据),得到CF和电压总谐波畸变率(total harmonic voltage distortion,VTHD)的变化趋势如图 3所示,CFL和LCD3次谐波电流幅值的变化趋势如图 4所示。从图 3中不难看出,VTHD的变化较大,但CF均小于
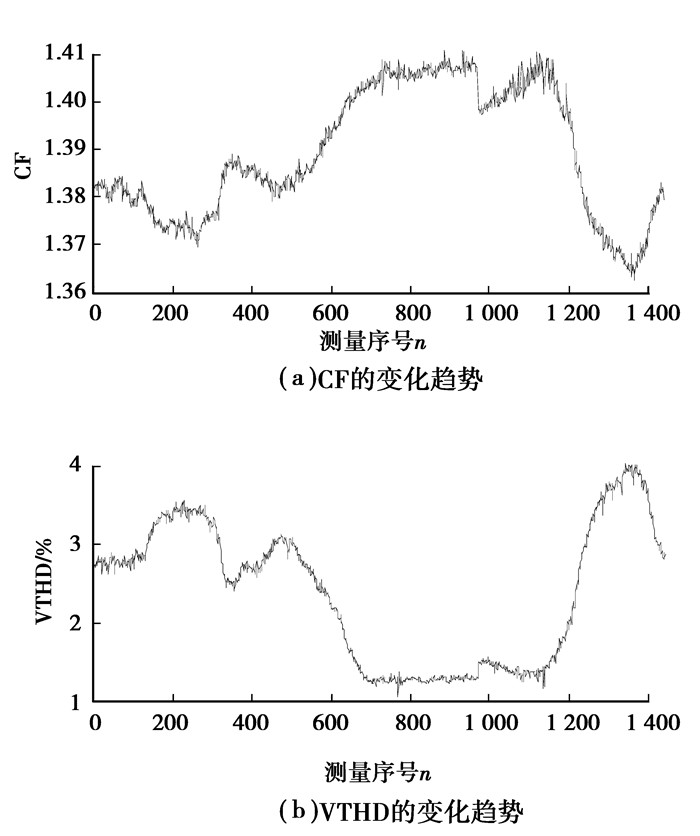
|
图 3 CF和VTHD的变化趋势 |
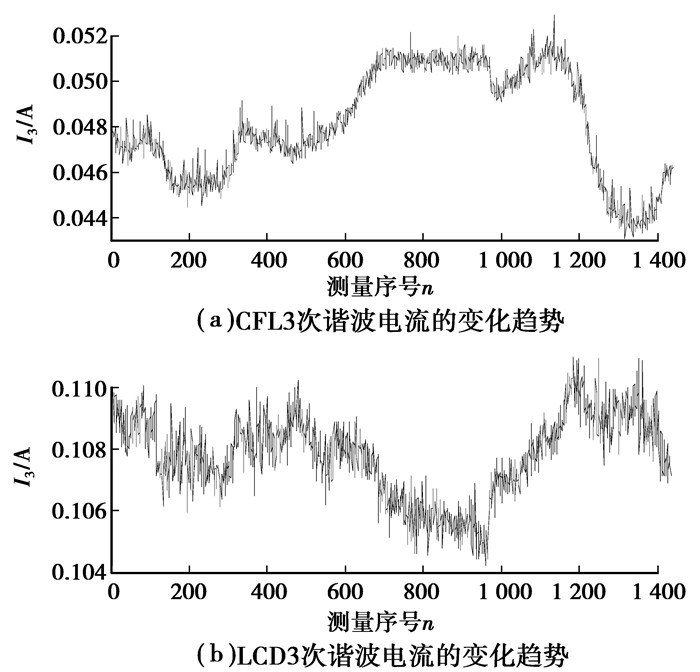
|
图 4 CFL和LCD3次谐波电流幅值的变化趋势 |
由于实际低压配电系统中电压表现为平坦波波形,非线性负荷的谐波电流将随电压的平坦特征而发生衰减效应[20]。CFL和LCD在某一标准余弦电压(基波电压幅值为227 V)下的3次谐波电流幅值分别为0.056 A和0.126 A,图 4中CFL和LCD的3次谐波电流最大值分别为0.52 A和0.112 A,均小于标准余弦电压下的电流值,存在明显的衰减效应(标准余弦电压由“可编程交流电源供应器”提供,文中除实测电压外,其他电压波形由此电源供应器产生,实验平台见下一节)。对于5、7次等谐波电流,可得到类似的结论。需特别注意的是,标准余弦电压基波电压幅值选为227 V是因为实测的1 440组数据中,最小的基波电压幅值为227 V,当选择大于227 V的基波电压幅值时,所体现的衰减效应将更明显。
表 1为CFL分别在2%和5%VTHD条件下,平坦波、尖顶波与标准余弦波(所有基波电压幅值均为220 V)的3、5次谐波电流数据(笔者还对LCD、台式计算机、笔记本电脑等非线性负荷进行过实验,其电流特性与CFL类似)。
| 表 1 CFL 3、5次谐波电流幅值 |
结合上述实测结果及表 1中数据可知:电压波峰系数CF是影响低压配电系统单相非线性负荷谐波电流的关键因素,主要体现在电流的波动大小及波动趋势上,其最终将对Norton模型参数的变化产生影响。
3 “非干预式”法获取负荷的Norton模型低压配电系统中,对于某一给定负荷,由于短时间内系统谐波阻抗及谐波源较为稳定,在负荷接入点处要获得显著地电压和电流的波动量是非常困难的,需要长时间的测量。为获取负荷的Norton模型参数,必须先得到负荷接入点处电压和电流的波动量,通过2种方式来实现电压的波动:采用“可编程交流电源供应器”作为电源,产生需要的各次谐波电压幅值和相角;利用负荷接入点处各次谐波电压的自然变化。这2种方式均为“非干预式”法,对系统不存在干扰因素。
3.1 电源供应器作为电源的Norton模型参数文中实验采用的“可编程交流电源供应器”为台湾致茂公司生产,其能产生1~50次谐波电压及它们之间的任意组合,各次谐波电压的幅值和相角都可以通过编程控制,误差在3%以内。采用此设备进行实验的示意图如图 5所示,采用NI-DAQ设备采集电压和电流,各次谐波电压和电流由FFT分析得到。
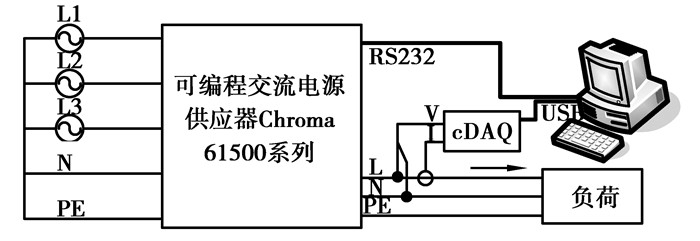
|
图 5 实验示意图 |
由上述电源供应器产生不同的电压波形(不同的CF及VTHD),计算得到LCD的3次谐波Norton模型参数如表 2所示,对于5、7次等谐波及其他非线性负荷,结论基本一致,在此不再赘述。
| 表 2 LCD 3次谐波Norton模型 |
从表 2中不难看出,Norton模型参数变化非常大,特别是模型等值阻抗Zch。显然,此类单相非线性负荷的Norton模型并不成立,其结论与文献[17]中的结论保持一致。由于实际低压系统电压呈现平坦波形,忽略表 2中含尖顶波的电压波形数据(表 2中加粗的数据),其参数变化将大大减小。这在一定程度上说明,电压波峰系数CF对此类单相非线性负荷Norton模型的成立起到了非常关键的影响。
3.2 实测条件下的Norton模型参数为进一步说明实际低压配电系统中,负荷Norton模型参数的变化情况,分别选择两种不同的基准电压(变化前的电压条件)进行阐述。
3.2.1 以标准余弦电压作为基准电压当选择标准余弦电压作为变化前的电压条件,以上一节实测到的1 440组电压作为变化后的电压条件,通过式(1)~(2)计算得到LCD的Norton模型参数如图 6所示。
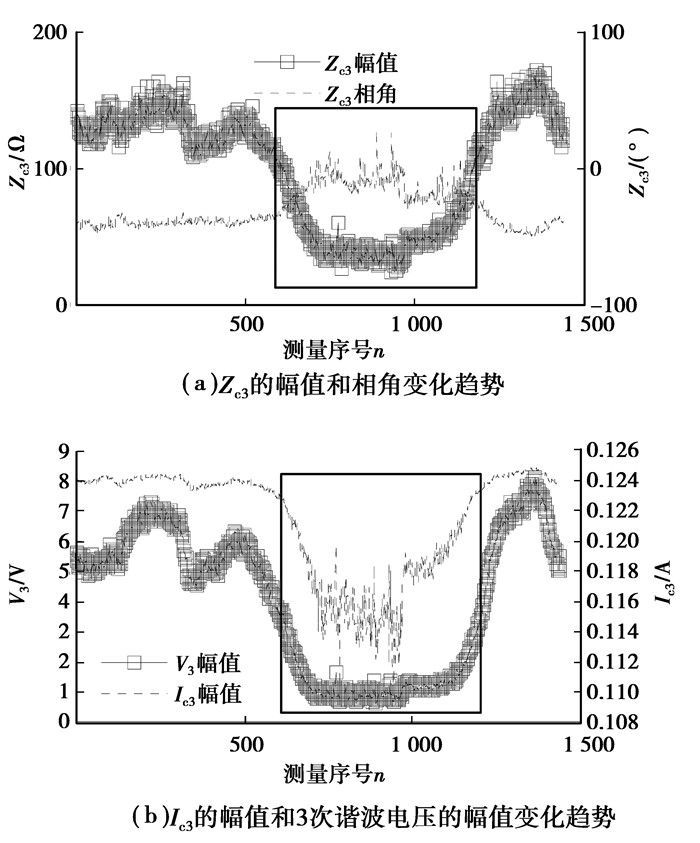
|
图 6 LCD3次谐波Norton模型参数及3次谐波电压的变化趋势 |
从图中不难看出:模型参数的变化是较小的,其保持着良好的一致性。理论上,选择标准余弦电压作为波动量法中变化前的电压,计算出的模型参数Ich应恒定不变,如式(3)所示,考虑电源供应器及测量的误差,其值也应保持基本不变,但实线框内的数据发生了较大的变化,可判断是由于减法误差导致的。且实线框内的数据,也不满足文献[17]给出的2次电压的变化至少不低于1%的条件。对于5、7次等谐波,其结论与3次谐波基本一致。对于CFL、笔记本电脑等非线性负荷,其模型参数变化都较小。
3.2.2 以负荷低谷时实测到的电压作为基准电压从图 6(b)中可以看出,实际低压配电系统中,负荷接入点处的谐波电压是不断变化的。一般而言,系统谐波电压总会存在一些比较小的值(负荷低谷时),比如图 6(b)中第700个和第1 160个测量值。分别选择这两个值作为变化前的电压条件,将图 6(b)中虚线框内对应的测量值(共700个点)作为变化后的电压条件,通过式(1)~(2)分别计算得到LCD的Norton模型参数如图 7所示。为了便于图形绘制,图中谐波电流放大了100倍。
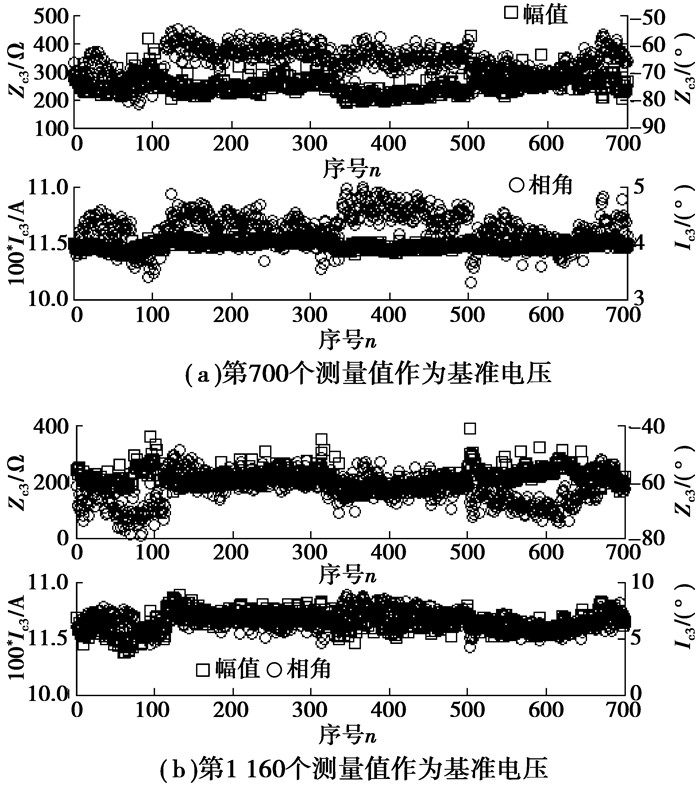
|
图 7 LCD3次谐波Norton模型参数 |
比较图 7(a)和图 7(b)不难看出:模型参数的变化是较小的,其保持着良好的一致性;但选择不同的基准电压,其模型参数会存在稍许差异。对于其他次谐波及非线性负荷,结论基本一致。
通过上述大量的实验说明:由于实际低压配电系统中电压呈现平坦波波形,其对负荷Norton模型的成立产生了有利条件,在某一基准电压条件下,模型参数的变化都较小;因此,在实际低压配电系统中,此类非线性负荷可以用Norton模型简化表示。
4 “干预式”法获取负荷的Norton模型低压配电系统中非线性负荷不同于大功率的工业负荷,单个或多个负荷的投切并不会影响系统谐波电压的显著变化,而这些小功率负荷的投切又具有随机性,在短时间内,为获取某一负荷或用户的Norton模型参数,很难通过“非干预式”法实现。往往需要借助于“干预式”法,其中最简单且容易实现的手段莫过于投切电容器[18-19]。图 8为电容投切的示意图。
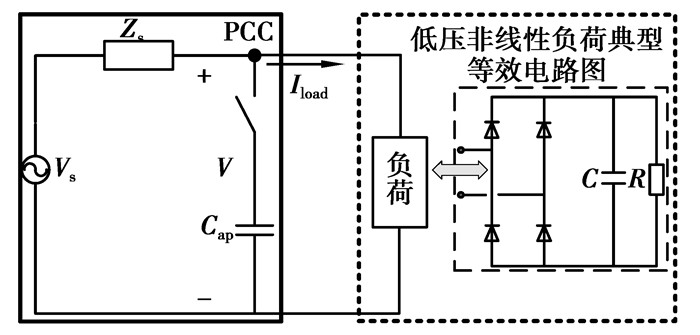
|
图 8 电容器在PCC处投切 |
系统侧阻抗Zs由所在处的短路容量决定,其值很小,为毫安级。对于单独一个非线性负荷或用户,在电容未投入时,其在Zs上的电压降非常小,可以忽略不计。因此,电容投切前,可将系统侧等效电压源Vs用PCC处测量到的电压Vpre表示;电容投切后,PCC处的电压Vpost几乎由图 8中实框内的RLC串联电路决定。
分别取负荷高峰和低谷时实测到的2组电压(负荷高峰:CF=1.383 2、VTHD=3.18%;负荷低谷:CF=1.403 2、VTHD=1.28%)及标准余弦电压作为系统侧的电压源,负荷用CFL等效电路(图 8中虚线框内所示整流电路)表示,按图 8所示在Simulink中建立仿真电路图,图中各元件参数:Zs=0.03 Ω、Cos=0.2;Cap=3 000 uF;C=3.55 uF;R=5 154 Ω。通过仿真计算获得CFL的3次谐波Norton模型参数如表 3所示(表 3中粗体的数据即为“干预式”法下的模型参数)。表 3中“电容投入”表示负荷高峰时,投入电容后的电压(CF=1.366 8、VTHD=5.13%)。
| 表 3 CFL 3次谐波Norton模型 |
从表 3中不难看出,“干预式”法与“非干预式”法获取的Norton模型参数会存在一定的差异。
5 分析与讨论在实际低压配电系统中,由于系统电压呈现出平坦特征,因此无论采用“干预式”法或“非干预式”法引起负荷接入点处电压发生显著地波动,波动量法表达式中变化前(或变化后)的谐波电压和谐波电流将体现平坦波电压条件下的谐波特性,比如负荷谐波电流发生衰减效应[3-4, 20]。电压所表现出的平坦特征及此类非线性负荷在这种电压下产生的衰减效应对Norton模型的成立是非常有利的,表 2中的数据也直观地说明了这点。同时通过大量的实验也说明,在实际低压配电系统中,此类非线性负荷用Norton模型简化表示是可行的。
但针对同样的实测数据,选择不同基准电压,其模型参数的均值(集中点)会出现一定的差异,如表 3和表 4所示。表 4列出了“非干预式”法获取LCD模型参数均值的情况,均值由图 6和图 7中的值得到。出现这种差异是因为此类非线性负荷模型参数的求取很大程度上依赖于电压和电流的波动量,通过选择不同的基准电压与实测电压构成的波动量去计算模型参数,其均值必然会存在差异,这也是波动量法求取此类非线性负荷Norton模型参数所固有的缺陷。
| 表 4 LCD 3次谐波Norton模型均值 |
实际上,无论采用“干预式”法或“非干预式”法去构造电压和电流的波动量,通过波动量法计算得到的Norton模型反映的是这2种电压波形条件下的电流特性,由于实测电压表现平坦特性,基准电压也应选择平坦波形,使其电流特性更接近,从而有利于得到更稳定的Norton模型。
宏观上,通常将非线性负荷用谐波电流源进行等效,将线性负荷用RLC电路进行等效。微观上,非线性负荷谐波电流会受输入端电压的影响,且不同负载,其影响大小也不尽相同。对于线性负荷,模型参数并不依赖于波动量,保持恒定;对于非线性负荷,电压变化引起电流的变化都将通过Norton模型来反映,其电流源部分反映非线性负荷的谐波源特性,其阻抗部分反映不同电压畸变对负荷谐波电流输出量的影响,选择不同的基准电压,通过电流源及阻抗部分反映的模型参数值也不仅相同,这正是均值存在差异的根本原因。
事实上,这种差异对于谐波潮流分析并没有影响,但对于谐波源识别却是个不容忽视的问题。负荷对PCC处的谐波贡献水平主要取决于PCC处谐波电压、系统谐波阻抗及负荷侧的等效谐波电流源,选择不同的基准电压致使负荷侧的等效谐波电流源存在的差异,将最终导致估计负荷谐波贡献水平的不同。表 4中由于选择不同的基准电压,得到LCD3次谐波电流源的差异约为20%,这种差异必然反映在其对PCC处的谐波贡献水平上。对比“干预式”法和“非干预式”法得到CFL的模型参数(如表 3),也可以得到类似的结论。实际上,对于不同负荷,其差异也不同。若在低压配电系统中,广泛运用Norton模型评估负荷对PCC处的谐波贡献水平,其准确性有待研究。
在实际低压配电系统中,针对不同非线性负荷组合的Norton模型及对PCC处谐波贡献水平的定量分析及准确性分析将在下一步工作中进行。
6 结论从实验的角度出发,结合仿真分析,对波动量法获取负荷的Norton模型参数变化的原因进行了探讨,得出影响负荷Norton模型成立的关键因素—波动量法变化前后电压和电流的选取。通过合理选择基准电压,低压配电系统中单相非线性负荷能用Norton模型进行简化表示。但是不同的基准电压得到的Norton模型参数也会存在差异,这种差异对谐波潮流分析并没有影响,但却影响评估负荷谐波贡献水平的准确性及可信度,这可能是将负荷等效成Norton模型来进行谐波贡献水平的评估而未得到学者们广泛认可的一方面原因。
| [1] | Waston N R, Bathurst G. Task force on harmonics modeling and Simulation[J]. IEEE Transactions on Power Delivery, 1999, 14(2): 579–587. DOI:10.1109/61.754106 |
| [2] | Xu W. Component modeling issues for power quality assessment[J]. IEEE Power Engineering Review, 2001, 21(11): 12–17. DOI:10.1109/MPER.2001.961998 |
| [3] | Mansoor A, Grady W M, Chowdhury A H, et al.An investigation of harmonics attenuation and diversity among distributed single-phase power electronic loads[C]//Proceedings of the 1994 IEEE Power Engineering Society Transmission and Distribution Conference, April 10-15, 1994, Chicago, IL. Pascataway:IEEE Press, 1994:110-116. |
| [4] | Nassif A B, Xu W. Characterizing the harmonic attenuation effect of compact fluorescent lamps[J]. IEEE Transactions on Power Delivery, 2009, 24(3): 1748–1749. DOI:10.1109/TPWRD.2009.2021022 |
| [5] | Jing Y, Liang C, Nassif A B, et al. A frequency-domain harmonic model for compact fluorescent lamps[J]. IEEE Transactions on Power Delivery, 2010, 25(2): 1182–1189. DOI:10.1109/TPWRD.2009.2032915 |
| [6] | Jing Y, Liang C. Modeling of home appliances forpower distributed system harmonic analysis[J]. IEEE Transactions on Power Delivery, 2010, 25(4): 3147–3155. DOI:10.1109/TPWRD.2010.2051960 |
| [7] | Sun Y Y, Zhang G B, Xu W, et al. A harmonically coupled admittance matrix model for AC/DC converters[J]. IEEE Transactions on Power Systems, 2007, 22(4): 1574–1582. DOI:10.1109/TPWRS.2007.907514 |
| [8] | Fauri M. Harmonic modelling of non-linear load by means of crossed frequency admittance matrix[J]. IEEE Transactions on Power Systems, 1997, 12(4): 1632–1638. DOI:10.1109/59.627869 |
| [9] |
赵勇, 张涛, 李建华, 等.
一种新的谐波源简化模型[J]. 中国电机工程学报, 2002, 22(4): 47–52.
ZHAO Yong, ZHANG Tao, LI Jianhua, et al. A new simplifiedharmonic source model for harmonic analysis and mitigation[J]. Chinese Society for Electrical Engineering, 2002, 22(4): 47–52. (in Chinese) |
| [10] | Thunberg E, Soder L. A Norton approach to distribution network modeling for harmonic studies[J]. IEEE Transactions on Power Delivery, 1999, 14(1): 272–277. DOI:10.1109/61.736738 |
| [11] | Thunberg E, Soder L. On the performance of a distribution network harmonic Norton model[C]//Proceedings of the Ninth International Conference on Harmonics and Quality of Power, October 01-04, 2000, Orlando FL. Piscataway:IEEE Press, 2000, 3:932-937. |
| [12] | Abdelkader S, Abdelr M H, Osman M G. A Norton equivalent model for nonlinear loads[C]//Proceedings of 2001 Large Engineering Systems Conference on Power Engineering, July 11-13, 2001, Halifax, NS. Piscataway:IEEE Press, 2004:63-67. |
| [13] | Yang H, Pirotte P, De J E, et al. Harmonic emission levels of industrial loads statistical assessment[J]. International conference on large electric systems, 1996, 2(36): 306. |
| [14] | Xu W, Liu Y L. A method for determining customer and utility harmonic contributions at the point of common coupling[J]. IEEE Transactions on Power Delivery, 2000, 15(2): 804–811. DOI:10.1109/61.853023 |
| [15] | Emanuel A E. On the assessment of harmonic pollution of power systems[J]. IEEE Transactions on Power Delivery, 1995, 10(3): 1693–1698. DOI:10.1109/61.400958 |
| [16] |
龚华麟, 肖先勇, 刘亚梅, 等.
基于主导波动量筛选原理的用户谐波发射水平估计方法[J]. 中国电机工程学报, 2010, 30(4): 22–27.
GONG Hualin, XIAO Xianyong, LIU Yamei, et al. A method for assessing customer harmonic emission level based on the dominant fluctuation filtering principle[J]. Chinese Society for Electrical Engineering, 2010, 30(4): 22–27. (in Chinese) |
| [17] | Rylander M, Grady WM.Problems in the use of Norton equivalent models for single-phase nonlinear loads[C]//Proceedings of 2010 Power and Energy Society General Meeting, July 25-29, 2010, Minneapolis, MN. Piscataway:IEEE Press, 2010:1-7. |
| [18] | Mazin H E, Nino E E, Xu W, et al. A study on the harmonic contributions of residential loads[J]. IEEE Transactions on Power Delivery, 2011, 26(3): 1592–1599. DOI:10.1109/TPWRD.2010.2096236 |
| [19] | Nino E E, Xu W. Measurement of harmonic sources in three-wire single-phase supply systems[J]. IEEE Transactions on Power Delivery, 2007, 22(4): 2527–2533. DOI:10.1109/TPWRD.2007.905554 |
| [20] |
雍静, 娄方桥, 王一平, 等.
低压配电系统单相非线性负荷的谐波衰减效应研究[J]. 中国电机工程学报, 2011, 31(13): 55–62.
YONG Jing, LOU Fangqiao, WANG Yiping, et al. Investigation on the harmonic attenuation effect of single-phase nonlinear loads in low voltage distribution system[J]. Chinese Society for Electrical Engineering, 2011, 31(13): 55–62. (in Chinese) |
 2013, Vol. 36
2013, Vol. 36

