微流控技术以其微量、精确可控、实时观测等优点,使其在生物[1-3]、化工[4-6]等领域得到越来越广泛运用,实时精确检测微管中流体的运动状况,获取流体的粘度、在微管中流动时的剪切力等的需求越来越迫切。但由于其微管尺寸很小,常规运动检测方法无法运用,导致应用中量化计算受到极大限制,限制了其应用。由于无法知其运动速度,导致流动过程中剪切力无法计算,但剪切力在生物学研究中对细胞行为有重要影响。如Jianbin等[1, 7]在微流控芯片中实时改变剪切力对肾上皮细胞功能影响研究;Shuan、Haga等[8-9]对剪切力对血管内皮细胞和血管平滑肌细胞影响的研究,近年来微观尺度下剪切力对各种细胞增殖、迁移、粘附、凋亡等功能影响研究呈爆炸性增长趋势。生物学研究中微纳升流体粘度值测量极其重要,如研究蛋白质动力学[10]、酶动力学[11]的细胞质液粘度的测量;Jinkee等[12]测量悬液粘度和本质粘度进而得到在不同条件下buffer缓冲液中蛋白质和DNA构想的变化等微纳升体积液体粘度测量的研究。另外,在化工研究中,无法获取准确流动速度,对于控制反应混合时间进而控制产物等有较大难度,如Andrew[13]对于微流控芯片作为化学反应平台应用中,化学反应物流体的流速影响做了研究,得出在微尺度下流动状态层流或湍流转换与宏观尺度下不同,严重影响化学反应物共混层度的判断以至影响最终结果或产物;Monica等[14]指出了在具有持续流动特点的芯片实验室作为化学合成平台的应用领域中,除了芯片几何构型和制作材料等对反应影响外,流速控制对化学反应控制机产物生成控制中的重要作用,因此精确控制并测量流体流速至关重要;在新兴的微型粘度计中,粘度测量多通过速度测量得出,Zuoyan等[15]基于PDMS微型粘度计提及粘度算法,但多数测速方法仅适用于特定芯片构型或特定条件下测速,具有很大的运用局限性,难以用于其他微型粘度计粘度测量中,因此能精确地测量运动速度,并且可推广至各种微流控芯片速度测量的方法亟待提出。
基于图像处理由视频信息中提取需要目标的检测有大量文献报道。如Alan等[16]用帧差法进行视频信息中汽车、人等运动目标的检测;Changick等[17]自动快速精确在MPEG-4格式视频中提取运动目标的研究等。在微管流动运动检测中,有张波等[18]提出利用图像处理解决毛细管粘度计液面读取的问题报道,进而测量粘度较以前方法有较大提高。关于近期兴起微流控芯片等微纳米级尺度微管中流动研究较少。提出一种可精确测量微流控芯片中流体运动检测的方法:采用帧差法和形态学图像处理方法,获取精确运动轨迹图像,通过霍夫变换得到轨迹图像边缘所需直线,最终结合已知的流动时间获得结果。
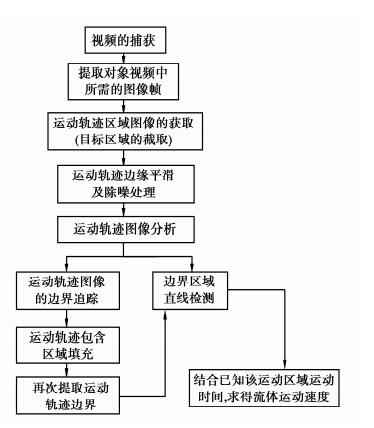
1 运动检测的基本流程运动检测的基本流程如图 1所示。
|
图 1 运动检测的基本流程 |
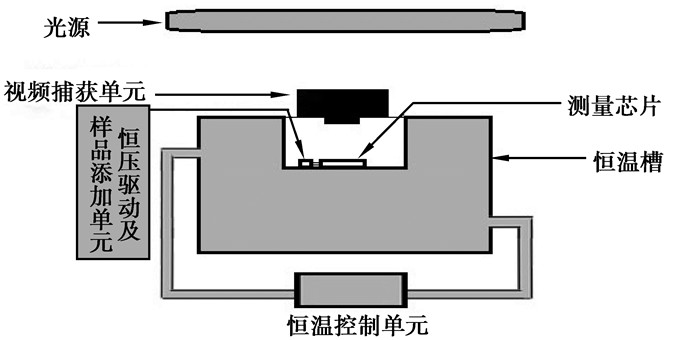
图 2为实验装置视频捕获部分的示意图,整部分处于暗室中(消除其他背景光的影响)。装置包括光源、恒温槽、录像采集装置、测量芯片,测量芯片旁固定有AutoCAD出图的标定刻度,刻度间距为2 mm,用以像素和实际流动距离的换算。光源位于采集录像装置的正上方,测量芯片固定于恒温槽中,相机采集录像位置在其正上方,捕获视场为芯片流动部分。微纳尺度芯片录像采集实验装置为荧光显微镜。图 3为实时捕获流动过程不同时刻帧图片。图片大小为1 280×720 pixels(像素)大小,分辨率为1像素大小,可通过调整同样长度所占像素数目多少来调整精确度,文中方法理论可致无限精确。
|
图 2 实验装置示意图 |

|
图 3 流量过程中不同时刻流体液面位置液面位置 |
目标提取是指利用灰度、颜色、纹理、形状等信息从视频序列中提取研究所需目标,该方法是图像工程中目标的特征提取和参数测量的基础。目前关于运动检测方法较多,较为流行的有:帧差法,光流法[19],背景减法及将几种方法混合起来检测目标运动的方法。由于帧差法思想简单,算法易实现,处理速度快,文中采用帧差法来提取运动目标。
为了去除不需要背景,减少后面计算量,从背景图像中将检测到的目标区域剪切出来。采取每间隔一定帧数图像取1帧图像用于帧差法运算,精确度随所取帧数增加而增加,由于运动目标的连续性较好,故取5帧图像。实现过程如下
| $ {d_i} = \left| {{I_L}\left( {x, y, 1 + i \times n} \right)-{I_L}\left( {x, y, 1} \right)} \right|, $ | (1) |
| $ \mathit{I}{\mathit{D}_{L1}}\left( {x, \mathit{y, i}} \right) = {d_0} + {d_1} + {d_2} + \cdots + {d_i}, $ | (2) |
| $ {\mathit{d}_\mathit{i}} = \left| {{I_L}\left( {x, y, \mathit{N}} \right)-{I_L}\left( {x, y, 1 + i \times n} \right)} \right|, $ | (3) |
| $ \mathit{I}{\mathit{D}_{L2}}\left( {x, \mathit{y, i}} \right) = {d_0} + {d_1} + {d_2} + \cdots + {d_i}。$ | (4) |
式中:di是相关2幅图像进行减法运算结果图像,IDL1/IDL2是帧差算法后叠加的图像,IL(x,y,i)和IL(x,y,1+i×n)分别是第1帧和第i+i×n帧亮度分量,i(i=1,2……N)表示帧数,N为所需图像的总帧数,n为选取相关帧时间隔帧数,一般选取图像采集设施每秒所能采集帧数,研究选取30。
对所得图像帧做帧差法运算后(见式(1)),进行图像叠加(见式(2)),二值化过程中最大限度除去背景中噪声,加强目标灰度,使得图像二值化过程中可选取较大阀值,更好去除背景噪声,以便后面在二值化图像中寻找运动轨迹端点。为了检测到运动轨迹图像全部端点,将所得图像再次进行帧差法运算后(见式(3))同样进行叠加(见式(4)),在2次叠加结果图像中搜寻运动轨迹图像端点。
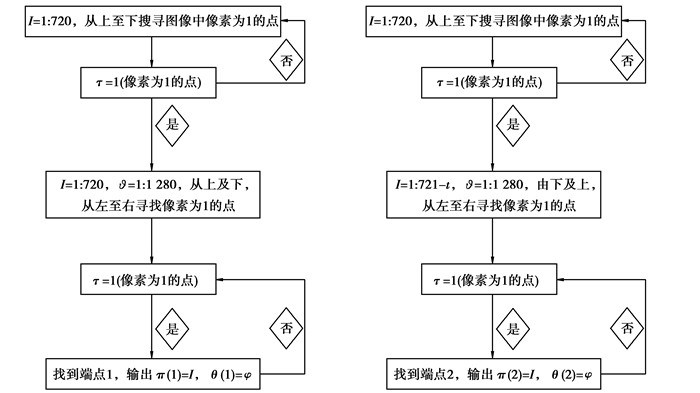
寻找所需区域端点的基本流程如图 4所示。
|
图 4 寻找所需区域端点的基本流程 |
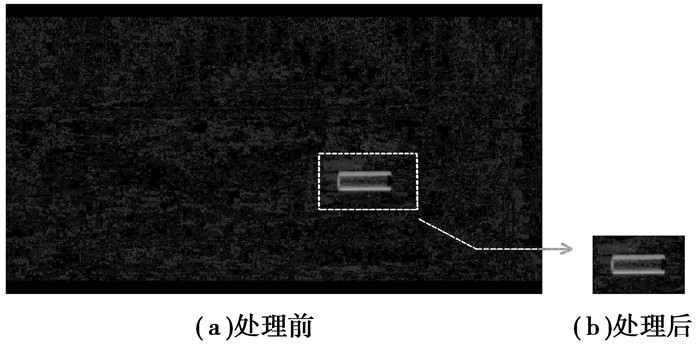
上述流程为左面2个端点检出流程,可按反方向进行搜索右面端点位置,进而求得图像运动轨迹的区域,然后以坐标最小值的端点外扩一定数目像素位置为起点,以最大最小值差值外扩一定数目的像素点作为长度和宽度,截取目标区域。处理前及经处理后获取运动轨迹图像如图 5所示。
|
图 5 处理前及经处理后获取的运动轨迹图像 |
由于录像现场照明条件变化、空气污染等因素影响,在所得轨迹图像边缘会有较大噪声影响,造成轨迹图像边缘不平滑,需要用数学形态学方法对图像进行平滑滤波处理,便于下一步数据的分析。数学形态学通过腐蚀、膨胀操作的各种组合完成图像的细化、骨架提取、图像分割等运算,一般操作对象为二值图像,但该操作对灰度图像有着很好的效果。数学形态学是建立在积分几何和随机集论基础上的,在结构元素作用下完成对整幅图像的处理(图像骨骼化、形态学滤波、细化和裁剪等),用于变换的结构元素类似于卷积核,其在图像上逐像素移动,以完成上述操作。
将得到的图像转为灰度图像I(图 6(a)),为进一步突出需要运动轨迹区域亮度带,去掉背景中干扰亮点,将所得图像进行亮度变换,进行图像增强,得到图像J(图 6(b)),为后面二值化做好准备。利用参数为[M,N]值的长方形结构元素对增强后的灰度图像进行开运算,得到图像J1(图 6(c))。原理如下:先对图像进行腐蚀后进行膨胀称为开操作,反之过程称为闭操作。利用结构元素b对图像f进行腐蚀定义为

|
图 6 运动轨迹图像边缘平滑及除噪处理 |
(f⊝b)(x,y)=min{f(x+x′,y+y′)-b(x′,y′)|(x′,y′)∈Db},Db为b的定义域,f(x,y)在f定义域外假设为+∞。
利用结构元素b对图像f进行膨胀定义为
(f⊕b)(x,y)=max{f(x-x′,y-y′)+b(x′,y′)|(x′,y′)∈Db},Db为b的定义域,f(x,y)在f的定义域外假设为-∞。
对图像f的开运算定于为:fb=(f⊝b)⊕b。
利用图像J减去经过开运算后的图像J1,得到流体运动轨迹图像J2(图 6(d)),将图像J2二值化,得到图像J3(图 6(e)),后用于运动轨迹的长度的求取。上述图像二值化过程中,如果图像亮度不均匀,会导致选取的阀值可能无法将需要区域与杂点分开,亦可能导致所需要区域直接被消除(图 6(f)),因此在图像二值化前,需要消除灰度图像中亮度不均匀问题后进行二值化。
分别用不同参数结构元素[M,N]对二值化的图像J3进行开闭运算,为分别达到消除运动轨迹外的杂点,并填充轨迹图像中空洞,进一步消除运动轨迹图像表面边缘不平整毛边等,可进行多次循环达到目的。因流动过程中环境相对稳定,流动也为稳定流动状态,故只采用开闭开的循环运算,处理流程如图 7所示。

|
图 7 运动轨迹边缘处理流程 |
经典的边缘检测方法是对图像按像素的某领域构造边缘检测算子,使用不同edge函数检测边缘,edge函数进行边缘检测的结果像素由于噪声、不均匀照明引起的边缘断裂和杂散亮度不连续而难以得到完整边缘特性,使后续运算无法执行,且运算量较大,运算时间长,因此文中采用基于四连通或八连通区域的轮廓跟踪法的边界跟踪法中bwboundaries函数进行边界跟踪。边缘跟踪法的基本原理是先根据图像特征,大步距的寻找边缘的起始点,然后从起始点开始,小步距递进式的寻找出各个要素点,最后再将这些要素点连成平滑的曲线[20]。边缘跟踪法的主要优点是速度快,它只需要对图像中的一部分像素进行处理,不必对每个像素点都进行处理,因此它的计算速度远远超过常用的边缘提取算法,较适用于长的、简单平滑的曲线,特别是直线段,图 8为可见边界跟踪法相较于edge函数各种边缘检测器算法的结果比较,因此采用边界跟踪法检测运动轨迹图像的边缘。

|
图 8 可见边界跟踪法与经典边缘检测器算法比较 |
笔者首先跟踪图像外边缘,然后利用所得元胞数组B所包含的矩阵,将所有边界值像素赋值为1,得到运动轨迹图像边界但得到边界仍非直线,有些许断点或弯曲,尤其是顶点区域(见图 9(a))。为了使直线检测更为精确,将矩阵B扩充为1个矩形(见图 9(b)),这个矩形长度等于矩阵最长的距离,宽度等于这个矩阵最宽的距离。获得边界平滑的图像,再对其进行边界跟踪的操作,得到所需连续无断点、无弯曲的运动轨迹图像的边界见(图 9(c))。为下面霍夫变换检测直线并求其长度,奠定基础。
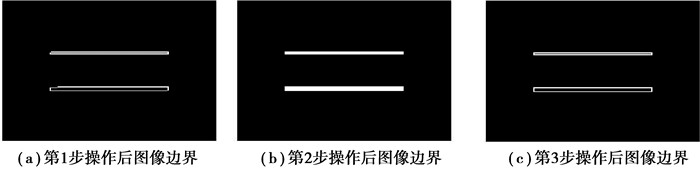
|
图 9 运动轨迹图像边界跟踪 |
采用具有良好的鲁棒性和抗干扰能力的Hough变换,检测运动轨迹边界的直线段,由于需处理图像为经过多步处理后的背景简单且无断点的连续直线段,因此用传统Hough即可得精确结果。Hough变换本质是一种从图像空间到参数空间的映射关系,通过Hough变换,把图像空间中复杂的图像特征信息转换为为参数空间中的聚类检测问题。其直线检测的基本原理为:在图像空间x-y中,过点(xi,yi)的直线有无数条,这些线对于某些a和b值来说,均满足y=axi+b。将该公式写为b=-xa+yi,并考虑ab平面(参数空间),可对1个固定点(xi,yi)产生单独1条直线。同理,第2个(xi,yi)在参数空间也具有与其相关的直线,这条直线和与(xi,yi)相关直线相交与点(a′,b′),其中a′和b′分别是xy平面上包含(xi,yi)和(xj,yj)的直线斜率和截距,这条直线上的所有点都有参数空间中相较于(a′,b′)的直线(见图 10)。
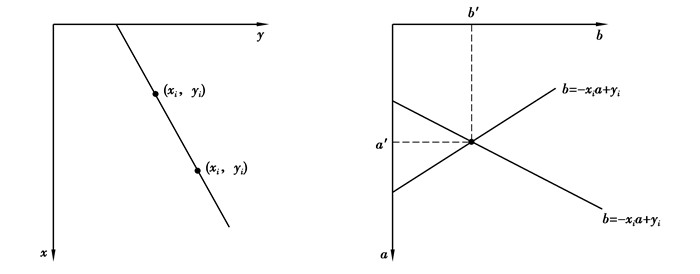
|
图 10 Hough变换直线检测的基本原理示意图 |
然而此种方法弊端为a(直线斜率)接近无限大,就是接近垂直方向。解决方法为采用直线标准表示法:x cos θ+y sin θ=ρ,极坐标情形跟直角坐标类似,参数ρ和θ分别代表直线距原点的法线距离和法线与x轴的夹角,交点(ρ’,θ’)对应于通过(xi,yi)和(xj,yj)的直线[21]。
该运算的图像背景简单,轨迹图像边界平滑,因此用常规Hough变换求得研究中流体运动距离,Hough变化检测直线极坐标如图 11所示。
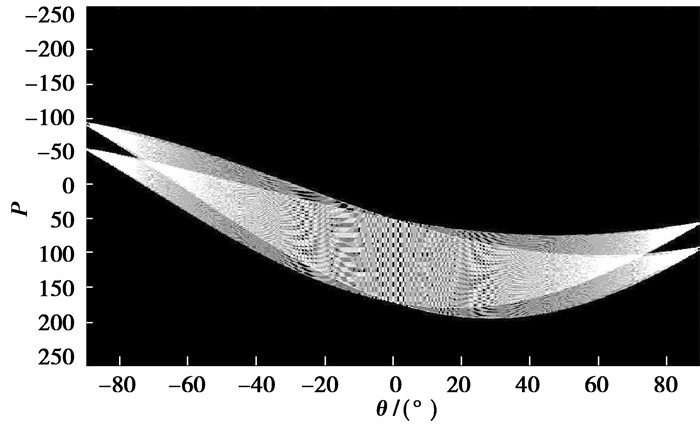
|
图 11 Hough变化检测直线极坐标 |
由于部分填充的矩形的两条边相距过近,若要检测出这2条直线需要提高Hough变换中的分辨率,这将导致运算量的提高。鉴于这2条边长度相同,故只需检测出1条即可,检测到直线中最长距离即为流体运动长度,结合运动时间求得流体运动速度。
3 结果 3.1 重复性和精确度验证所得结果经验证具有较好重复性和精确度,验证过程如下:
重复性:例证性研究采用流体为水,微流控芯片为直通道式芯片,通过在不同流动测量的视频中,分别在每一视频中流动稳定阶段中每隔1 s选取6 s中流体移动距离,共选取10段后采用文中方法进行处理,结果如表 1所示,表中T表示测试温度,℃;L表示相同时间流体在微管中移动距离,pixel(像素)。
| 表 1 检测结果 |
由表 1可见,流动稳定阶段,流体运动距离在不同起点移动距离间的标准差值σ非常小,因此该方法测量微管中流体移动距离具有很好的可重复性。
精确度理论可至无限精确,由于文中方法结果最小分辨率为1个像素值长度,可通过3方面调节实现精确度调节:1)相同条件下增加流动时间,调节运动轨迹目标区域的所占像素数目,提高精确度;2)改变录像输出格式,录像单帧图像越大,则目标区域占有像素数目越多,进而提高精确度;3)录像时放大录像区域,目标区域被放大相应增加目标区域所占用像素,进而增强结果精确度。在实验中,可结合自己对研究结果需要及研究设施综合考虑调节自己实验精确度。
3.2 方法广适性验证另外,可用于绝大多数构型微流控芯片速度检测,如对于经典3通道式微流控芯片实验室中流体的测速(如图 12所示)。
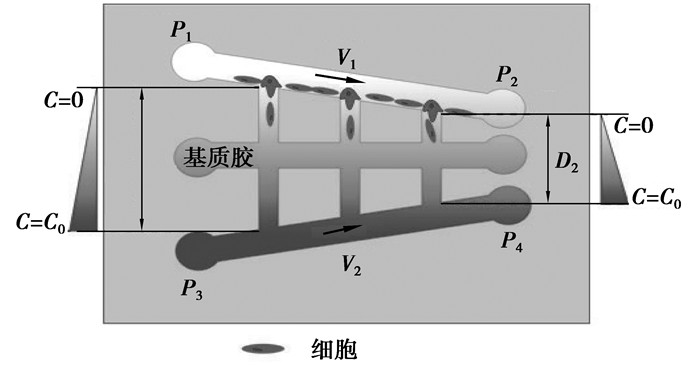
|
图 12 3通道式微流控芯片中流体的测速 注:P1,P2,P3,P4为各出口压力;D1,D2为通道间距离,D1≥D2;V1,V2为腔内液体流速,可以对内皮细胞施加不同大小的层流或湍流剪切力 |
选择尺度标记(Bar)10 μm视野下进行视频捕获,分析知10 μm占用像素数目约为6.33 pixels。选取该流体于芯片中灌胶速度的1/5情况下,8 s内的移动距离。经测量为324像素长度,结合上述结果可得到流体于芯片中的移动速度为64 μm/s。在芯片实验室中为模拟体内真实三维培养环境,在细胞与胶原共混灌注过程中,细胞悬液在微通道中流速决定灌注成功与否进而决定实验成败。另外细胞培养过程中,培养液流速产生剪切力对增殖或分化亦有重要影响,因而一个精确的量化运动速度值的测出具有十分重要的意义。
通过求得流体运动距离,结合其他已知粘度流体同样时间内运动的距离,在同样流动状态下可推测待测样品粘度,同时亦可结合选取图像时采取的帧数进而计算得出流体运动时间,依据长度和距离之间关系,求得流体运动速度,得出流动剪切力大小等数据。
4 结论结合视频捕获和图像分析技术,获取微流控芯片中流体运动状况。提出利用视频图像处理技术,获取流体运动距离,进而获悉流体运动速度,最终得到所需流体的粘度的方法。得到的流体运动速度经微流控芯片验证,测量精确,且重复性很好,使得微流控芯片参数的进一步量化。另外利用文中方法处理速度非常快,可用于生产中的在线测量等,为微流控芯片更广泛应用奠定了基础。
| [1] | Noort D N, Ong S M, Zhang C, et al. Stem cells in microfluidics[J]. Biotechnology Progress, 2009, 25(1): 52–60. DOI:10.1002/btpr.v25:1 |
| [2] | Elal J, Sorger P K, Jensen K F. Cells on chips[J]. Nature, 2006, 442: 401–403. |
| [3] | Liu T J, Li C Y, Li H J, et al. A microfluidic device for characterizing the invasion of cancer cells in 3-D matrix[J]. Electrophoresis, 2009, 30(24): 4285–4291. DOI:10.1002/elps.v30:24 |
| [4] | Demello A J. Control and detection of chemical reactions in microfluidic systems[J]. Nature, 2006, 442(7101): 394–402. DOI:10.1038/nature05062 |
| [5] | Ohno K I, Tzchikawak K, Manz A. Microfluidics:applications for analytical purposes in chemistry and biochemistry[J]. Electrophoresis, 2008, 29(22): 4443–4453. DOI:10.1002/elps.v29:22 |
| [6] | Pedro S G, Puyol M, Alonso C J. Continuous flow synthesis of nanoparticles using ceramic microfluidic devices[J]. Nanotechnology, 2010, 21(41): 1–6. |
| [7] | Wang J B, Heo J, Hua S Z. Spatially resolved shear distribution in microfluidic chip for studying force transduction mechanisms in cells[J]. Lab Chip, 2009, 10(2): 235–239. |
| [8] | Li Y S J, Haga J H, Chien S. Molecular basis of the effects of shear stress on vascular endothelial cells[J]. Journal of Biomechanics, 2005, 38(10): 1949–1971. DOI:10.1016/j.jbiomech.2004.09.030 |
| [9] | Haga J H, Li Y S J, Chien S. Molecular basis of the effects of mechanical stretch on vascular smooth muscle cells[J]. Journal of Biomechanics, 2007, 40(5): 947–960. DOI:10.1016/j.jbiomech.2006.04.011 |
| [10] | Ansari A, Jones C M, Henry E R, et al. The role of solvent viscosity in the dynamics of protein conformational changes[J]. Science, 1992, 256(5065): 1796–1798. DOI:10.1126/science.1615323 |
| [11] | Ellis R J. Macromolecular crowding:an important but neglected aspect of the intracellular environment[J]. Current Opinion in Structural Biology, 2001, 11(1): 114–119. DOI:10.1016/S0959-440X(00)00172-X |
| [12] | Lee J, Tripathi A. Intrinsic viscosity of polymers and biopolymers measured by microchip[J]. Analytical Chemistry, 2005, 77(22): 7137–7147. DOI:10.1021/ac050932r |
| [13] | Demell O A J. Control and detection of chemical reactions in microfluidic systems[J]. Nature, 2006, 442(7101): 394–402. DOI:10.1038/nature05062 |
| [14] | Brivio M, Verboom W, Reinhoudt D N. Miniaturized continuous flow reaction vessels:influence on chemical reactions[J]. Lab Chip, 2006, 6(3): 329–344. DOI:10.1039/b510856j |
| [15] | Han Z Y, Ang X J, Zheng B. A PDMS viscometer for microliter Newtonian fluid[J]. Journal of Micromechanics and Microengineering, 2007, 17(9): 1828–1834. DOI:10.1088/0960-1317/17/9/011 |
| [16] | Lipton A J, Fujiyoshi H, Patil R S. Moving target classification and tracking from real-time video[C]//Proceedingd of the 1998 Fouth IEEE Workshop on Applications of Computer Vision, October 19-21, 1998, Princeton, NJ.Piscataway:IEEE Press, 1998:19-21. |
| [17] | Kim C, Hwang J N. Fast and automatic video object segmentation and tracking for content-based applications[J]. IEEE Transactions on Circuits and Systems fr Video Technology, 2002, 12(2): 122–129. DOI:10.1109/76.988659 |
| [18] |
张波, 张维成.
图像处理在粘度测量中的应用[J]. 电脑与电信, 2008(8): 82–84.
ZHANG Bo, ZHANG Weicheng. The application of image processing technology in viscosity measurement[J]. Computer & Telecommunication, 2008(8): 82–84. (in Chinese) |
| [19] | Horn B K P, Schunck B G. Determining optical flow[J]. Artificial Intelligence, 1981, 17(1-3): 185–203. DOI:10.1016/0004-3702(81)90024-2 |
| [20] |
贺忠海, 王宝光, 廖怡白, 等.
图像处理中的边缘跟踪法研究[J]. 仪器仪表学报, 2001, 22(Sup3): 261–262.
HE Zhonghai, WANG Bbaoguang, LIAO Yibai, et al. Study on boundary tracking method used in image processing[J]. Chinese Journal of Scientific Instrument., 2001, 22(Sup3): 261–262. (in Chinese) |
| [21] | 冈萨雷斯, 伍兹, 埃丁斯, 等. 数字图像处理:MATLAB版[M]. 北京: 电子工业出版社, 2005. |
 2013, Vol. 36
2013, Vol. 36


