b. 重庆大学 机械工程学院, 重庆 400030
b. College of Mechanical Engineering, Chongqing University, Chongqing 400044, China
近年来,随着啁啾脉冲放大技术(chip pulse amplification,CPA)[1]的广泛应用,获得更高能量、更高强度的超短脉冲激光成为必需。脉冲压缩系统中的关键元件-压缩光栅(pulse compression grating,PCG)其尺寸要求在米量级,但是这样大口径的光栅很难制造,而通过拼接的方法来获得大口径光栅是解决上述问题的有效途径[2]之一,而且已经获得了初步的成果。
针对光栅拼接的高稳定性的控制要求[3],需要采用闭环控制来实现其动态稳定性。Bunkenburg等[4-5]提出了配备了马赫—曾德尔干涉仪的拼接光栅的锁相控制;Qiao等[6]提出自动拼接的干涉分析法,而且第一次提出了由2块大口径拼接光栅组成压缩器,每块拼接光栅都使用干涉拼接技术[7]由4块子光栅拼接而成;Cotel等[8]证明子光栅的远场强度可以由干涉仪测量其波阵面得到,但是并没有提及基于远场的自动闭环拼接方法。最近,Hideaki Habara等[9]利用三轴运动传感器实现了高精度拼接光栅压缩器装置FIREX;绍忠喜等[10]对5自由度的宏/微光栅拼接装置进行了控制算法设计;Yuchuan Yang等[11]分析了拼接光栅的锁相控制。
PID算法作为自动控制领域中经典的控制理论由于其结构简单、鲁棒性好,被广泛用于生产过程中的自动控制。生产实践中,控制对象往往具有复杂性和不确定性[12],传统的PID算法结构简单,应用于生产实践中有一定的局限性,易产生饱和遗失,抗干扰性能差等[13]。在实际应用时,大多都对PID算法进行了改进,例如积分分离,不完全微分等改进。
笔者结合实际项目,分析了拼接光栅四维误差调整的数学模型,采用“锁存补偿法”与“四点中心差分法”对增量式PID算法进行改进,开发了适用于拼接光栅的PID控制算法,并且通过实验验证其可行性。
1 拼接光栅四维误差调整的数学模型以2块光栅拼接为例,它们的相对位置有6个方向的变化,X、Y、Z三维方向的平移和旋转,其中沿刻线方向的平移偏差只造成光束的能量损失,可以忽略[14]。根据文献[15]的分析,X向的平移误差与Z向平移误差配对补偿,其位相差可以由调节Z向平移来补偿。因此,子光栅拼接时只需要对动光栅进行四维误差(沿Z向的平移误差和绕X、Y、Z轴的旋转误差)的调整。
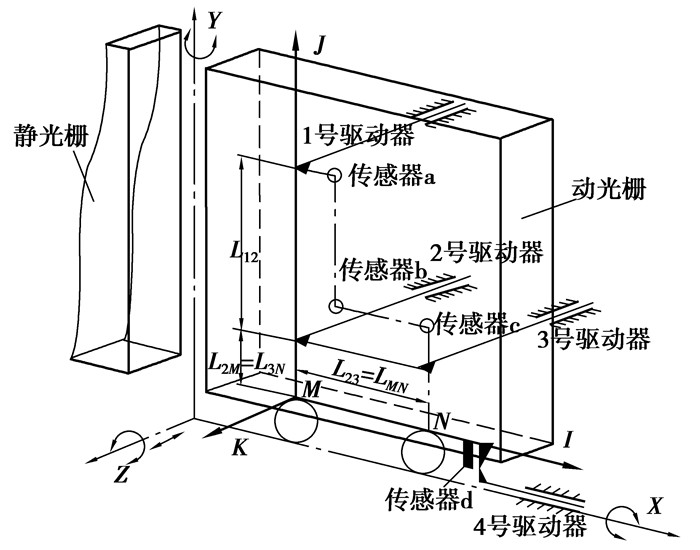
拼接光栅的调整简图,如图 1所示,驱动器和传感器的位置采用“L”型布置[16],1、2、3号驱动器用于调整绕X、Y轴的旋转和沿Z向的平移,4号驱动器调整绕Z轴的旋转。在实际的调整过程中,动光栅绕X、Y轴旋转的调整轴线分别为I、J轴,绕Z轴旋转和沿Z向平移的调整轴线为K轴。点M、N为支撑点,其距离为LMN,驱动器2、3号的中心距为L23,且L23= LMN,驱动器1、2号的中心距为L12,驱动器2号和M的距离为L2M,驱动器3号和N的距离为L3N,且L2M=L3N,驱动器4号和M的距离为L4M。
|
图 1 拼接光栅调整简图 |
设绕X、Y、Z的旋转误差分别为θX、θY、θZ,沿Z向的平移误差为ΔZ,驱动器1、2、3、4号的驱动位移分别为S1、S2、S3、S4。欲将动光栅由实际位置调整到理想位置,需要进行调整。
1.1 Z向的平移ΔZ沿Z向的平移是沿着K轴进行平移调整的。为了使得动光栅沿着Z向平移,根据3点定面原理,只需要将1、2、3号驱动器同时沿Z向驱动相同位移S,即可实现光栅面在Z向的平移,此时4号驱动器应该保持当前驱动位移不变,则
| $ \Delta Z = S, $ | (1) |
故,欲获得Z向的平移ΔZ,各驱动位移为
| $ {S_1} = {S_2} = {S_3} = \Delta Z, $ | (2) |
S4保持当前值不变。
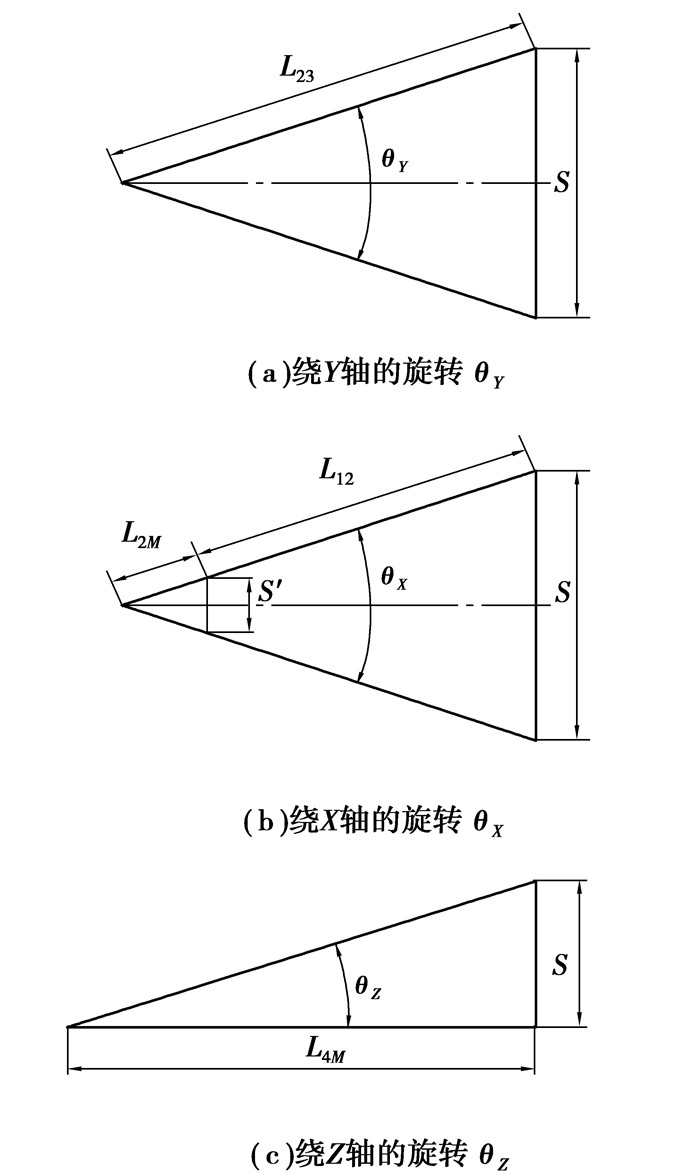
1.2 绕Y轴的旋转θY绕Y轴旋转的实际调整轴线为J轴,因此,可以锁定1、2、4号驱动器,保持其当前驱动位移不变,将3号驱动器向前驱动位移S,即可以实现绕Y轴的旋转θY。根据弧长公式,如图 2(a)所示,可得
|
图 2 三维旋转调整 |
| $ {\theta _Y} = \frac{S}{{{L_{23}}}}。$ | (3) |
故欲获得绕Y轴的旋转θY,各个驱动器的驱动位移为
| $ {S_3} = {\theta _Y}{L_{23}}, $ | (4) |
S1,S2,S4保持当前值不变。
1.3 绕X轴的旋转θX根据前面的分析,绕X轴的旋转的实际调整轴线为I轴,因此在调整绕X轴的旋转时1、2、3号驱动器都需要动作。将1号驱动器沿Z向驱动位移S,2、3号驱动器与1号同向驱动相等位移S’,即可以实现绕X轴的旋转θX,此时4号驱动器应该保持当前驱动位移不变,如图 2(b)所示,根据弧长公式得
| $ {\theta _X} = \frac{S}{{{L_{12}} + {L_{2M}}}} = \frac{{S'}}{{{L_{2M}}}}, $ | (5) |
故欲获得绕X轴的旋转θX,各个驱动器的驱动位移为
| $ \begin{array}{l} {S_2} = {S_3} = {\theta _X}{L_{2M}},\\ {S_1} = {\theta _X}\left( {{L_{12}} + {L_{2M}}} \right), \end{array} $ | (1.6) |
S4保持当前值不变。
1.4 绕Z轴的旋转θZ绕Z轴的旋转调整轴线是K轴,只需要4号驱动器沿Y向驱动位移S,此时应该锁定1、2、3号驱动器,保持其当前驱动位移不变,便可以实现绕Z轴的旋转θZ,由图 2(c),可得
| $ {\theta _Z} = \frac{S}{{{L_{4M}}}}。$ | (7) |
故欲获得绕Z轴的旋转θZ,各个驱动器的驱动位移为
| $ {S_4} = {\theta _Z}{L_{4M}}, $ | (8) |
S1,S2,S3保持当前值不变。
通过以上分析,得出2块拼接光栅四维误差调整数学模型为
| $ \left\{ \begin{array}{l} \Delta Z = S,\\ {\theta _Y} = \frac{S}{{{L_{23}}}},\\ {\theta _X} = \frac{S}{{{L_{12}} + {L_{2M}}}} = \frac{{S'}}{{{L_{2M}}}},\\ {\theta _Z} = \frac{S}{{{L_{4M}}}}。\end{array} \right. $ | (9) |
此模型是拼接光栅控制系统的控制算法的理论依据。
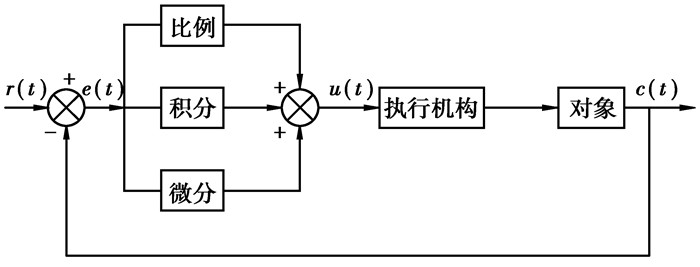
2 改进PID算法的分析PID控制是一种过程控制算法,主要由3个部分组成:测量、比较和执行。在生产过程中,通过测量值和期望值的比较得到偏差值,通过偏差值来调节控制器,实现对系统输出值的控制。PID控制系统的原理框图如图 3所示。
|
图 3 PID控制系统原理框图 |
在工程实际中,数字PID有2种形式,位置式PID算法和增量式PID算法。而增量式PID算法相比位置式PID算法较为容易实现无冲击的手动/自动转换,累积计算误差小,抗干扰能力强。增量式PID算法的数字形式
| $ \begin{array}{*{20}{c}} {\Delta u\left( n \right) = u\left( n \right) - u\left( {n - 1} \right) = }\\ {{K_{\rm{P}}}\left[ {e\left( n \right) - e\left( {n - 1} \right)} \right] + {K_{\rm{P}}}\frac{T}{{{T_{\rm{i}}}}}e\left( n \right) + }\\ {{K_{\rm{P}}}\frac{{{T_{\rm{d}}}}}{T}\left[ {e\left( n \right) - 2e\left( {n - 1} \right) + e\left( {n - 2} \right)} \right],} \end{array} $ | (9) |
式中:u(n)为第n次采样时刻的输出值;e(n)为第n次采样时刻的偏差;Kp为比例系数,KpT/Ti为积分系数,KpTd/T为微分系数。
增量式PID算法虽然优于位置式PID,但是也存在着不足之处,可能会发生比例微分饱和,抗干扰能力需要提高[12]。针对拼接光栅高精度、高稳定性的控制要求,对增量式PID算法进行以下2点改进,将改进后的增量式PID算法作为拼接光栅闭环控制算法。
2.1 避免饱和遗失增量式PID算法相比位置式PID算法不会出现积分饱和,但是由于控制系统中执行器本身的控制范围限制,在增量式PID算法中,若发生控制系统故障或者外部环境激励突变而使得偏差发生跃变,导致计算的增量过大,进而使得输出控制量超过执行器的控制范围,从而发生饱和使得部分增量信息遗失[17]。拼接光栅控制系统的结构复杂,控制精度要求非常高(亚微米量级),其执行器的行程和分辨率是亚微米量级,调整结构的细微故障和外部环境激励的突变都有可能会造成饱和遗失。因此,为了避免在拼接光栅自动调整过程中出现饱和遗失,采用“锁存补偿法”对增量式PID进行改进。
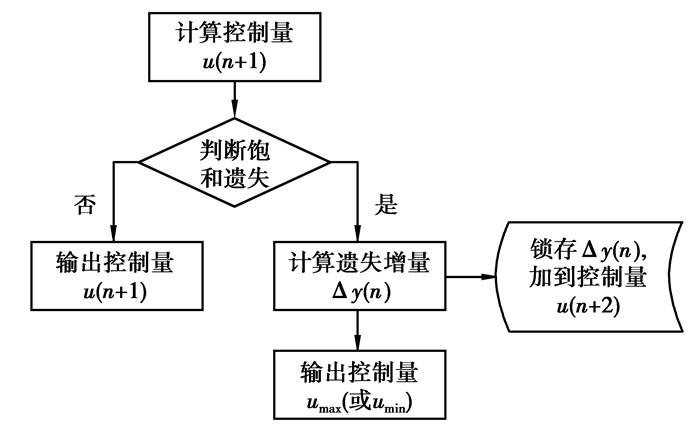
锁存补偿法的基本思想就是使用锁存器将第n次遗失的增量信息Δy(n)锁存起来,加到第n+1次的输出控制量里面,其控制原理如图 4所示。设执行器控制量的限制为umin和umax,第n次的计算的增量为Δu(n),第n次的控制量为u(n),第n-1次遗失的增量信息Δy(n-1),则第n+1次的控制量为
|
图 4 锁存补偿法控制原理 |
| $ u\left( {n + 1} \right) = u\left( n \right) + \Delta u\left( n \right) + \Delta y\left( {n - 1} \right), $ | (10) |
如果u(n+1)> umax(或 < umin),则第n+1次实际的输出控制量为umax(或umin),从而发生饱和遗失,而遗失的增量信息
| $ \begin{array}{*{20}{c}} {\Delta y\left( n \right) = u\left( {n + 1} \right) - {u_{\max }}}\\ {\left( {或\; = \;{u_{\min }} - u\left( {n + 1} \right)} \right)。} \end{array} $ | (11) |
此时使用锁存器将增量信息Δy(n)保存起来,等到计算控制量u(n+2)时,再加进去,如此循环下去。
2.2 四点中心差分法抗干扰数字PID算法式是对模拟PID控制式的近似,其中用和式代替了积分项,用差分代替了微分项。在各项中,差分对数据误差和噪声特别敏感,一旦出现干扰,通过差分项的计算有可能引起很大的控制量变化[18]。在数字PID算法中,干扰通过微分项对控制的影响是主要的。而且微分成分在PID调节器中是必要的,不能简单将其弃去。拼接光栅的环境虽然经过规范,但是仍然存在着很多不定突变,比如空调振动频率的突变、地面震动频率的突变、工作人员引起的扰动等,这些随机干扰都会在一定程度上影响整个拼接系统的稳定性,为了保持拼接光栅的长时间稳定,能够抑制随机干扰,采用“四点中心差分法”对微分项进行修改。
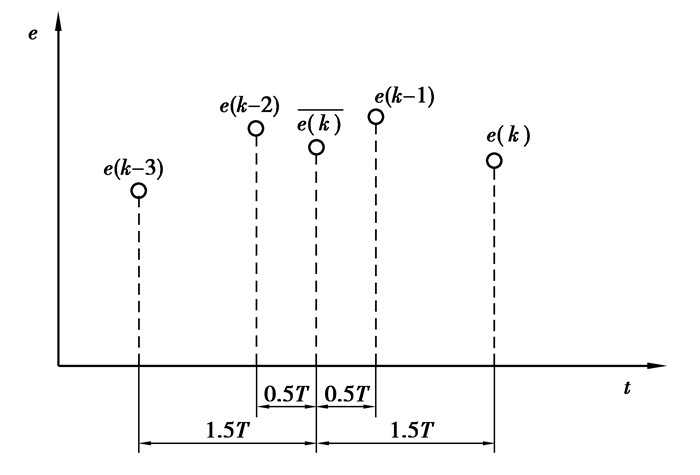
四点中心差分法的基本思想是首先将微分系数KpTd/T选得比理想情况下稍小,然后在组成差分时,不直接用现时的偏差e(n),而是使用现在和过去共4个偏差值的平均值作为基准,即
| $ \begin{array}{*{20}{c}} {\overline {e\left( k \right)} = \frac{1}{{4T}}\left[ {e\left( k \right) + e\left( {k - 1} \right) + } \right.}\\ {\left. {e\left( {k - 2} \right) + e\left( {k - 3} \right)} \right]。} \end{array} $ | (12) |
然后通过加权求和的形式构成近似微分项
| $ \begin{array}{*{20}{c}} {\frac{{\Delta \overline {e\left( k \right)} }}{T} = \frac{1}{{4T}}\left( \begin{array}{l} \frac{{e\left( k \right) - \overline {e\left( k \right)} }}{{1.5}} + \\ \frac{{e\left( {k - 1} \right) - \overline {e\left( k \right)} }}{{0.5}} + \\ \frac{{\overline {e\left( k \right)} - e\left( {k - 2} \right)}}{{0.5}} + \\ \frac{{\overline {e\left( k \right)} - e\left( {k - 3} \right)}}{{0.5}} \end{array} \right) = }\\ {\frac{1}{{6T}}\left( {e\left( k \right) + 3e\left( {k - 1} \right) - 3e\left( {k - 2} \right) - e\left( {k - 3} \right)} \right),} \end{array} $ | (13) |
|
图 5 四点中心差分加权求和近似微分 |
将式(13)替代式(9)中的差分项
| $ \frac{1}{T}\left[ {e\left( n \right) - 2e\left( {n - 1} \right) + e\left( {n - 2} \right)} \right], $ |
上式分解为2个一阶差分
| $ \begin{array}{*{20}{c}} {\frac{1}{T}\left[ {e\left( n \right) - e\left( {n - 1} \right)} \right]}\\ {和\; - \frac{1}{T}\left[ {e\left( {n - 1} \right) - e\left( {n - 2} \right)} \right],} \end{array} $ |
k分别取n和n-1。得到改进后的增量式PID算法为
| $ \begin{array}{*{20}{c}} {\Delta u\left( n \right) = {K_{\rm{P}}}\left[ {e\left( n \right) - e\left( {n - 1} \right)} \right] + {K_{\rm{P}}}\frac{T}{{{T_i}}}e\left( n \right) + }\\ {{K_{\rm{P}}}\frac{{{T_{\rm{d}}}}}{{6T}}\left[ {e\left( n \right) + 2e\left( {n - 1} \right) - 6e\left( {n - 2} \right) + } \right.}\\ {\left. {2e\left( {n - 3} \right) + e\left( {n - 4} \right)} \right]。} \end{array} $ | (14) |
由上式可知,经过四点中心差分法修改过后的增量式PID算法的控制增量与现在及过去共连续5次的偏差e相关。
四点中心差分法相对于普通增量式PID算法在组成微分项的差分时,使用了现时和过去共4个偏差的平均值,使用平均值法来削弱干扰,而普通的增量式PID却是直接使用现时的偏差组成差分。因此,四点中心差分法相比普通的增量式PID算法,具有较好的抗干扰能力。
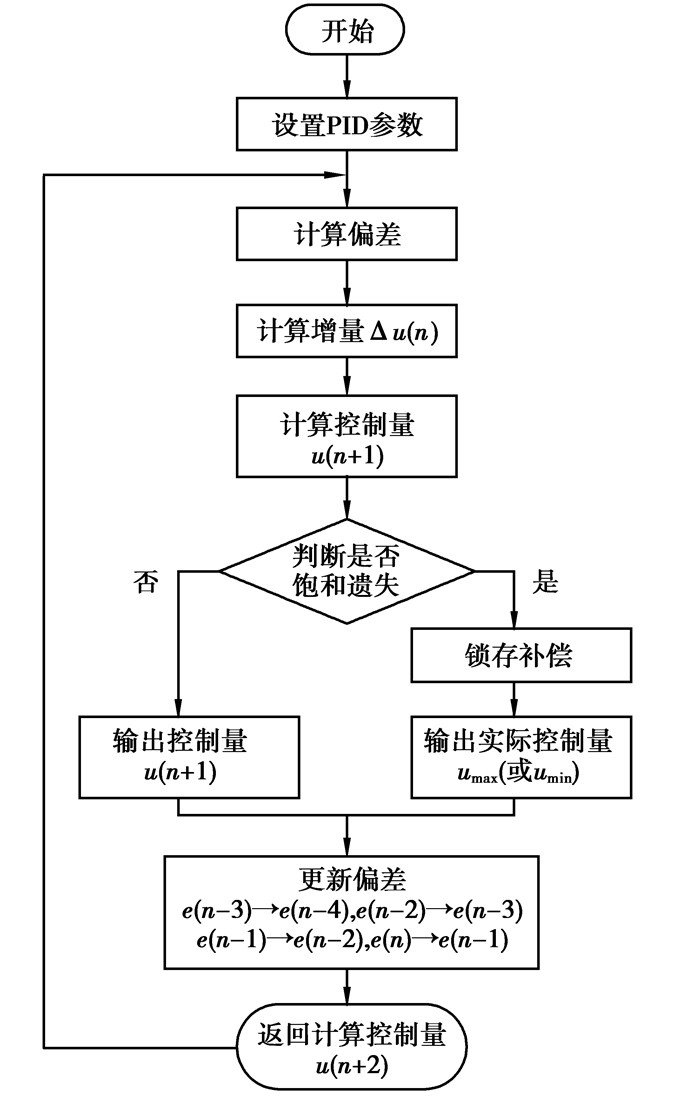
2.3 拼接光栅闭环控制的程序流程通过上述2个方面的改进,光栅拼接闭环自动控制算法的程序流程如图 6所示。在控制过程中,首先根据式(9)手动调整动光栅,使得光斑重合,然后标定传感器的值作为初始值,接着开始闭环自动调整。闭环控制过程中,首先需要设置PID参数Kp,Ti,Td和采样时间T,每次采样过程中将采集的位移与传感器标定的初值比较计算得到偏差e(n),e(n-1),e(n-2),e(n-3),e(n-4),根据式(14)和式(10)计算增量Δu(n)和控制量u(n+1),然后判断是否发生饱和遗失,如果遗失,进行锁存补偿,最后输出控制量u(n+1)。在输出控制量u(n+1)后,需要更新偏差值为计算输出控制量u(n+2)做准备。依次将e(n-3)赋值给e(n-4),e(n-2)赋值给e(n-3),e(n-1)赋值给e(n-2),e(n)赋值给e(n-1),以实现偏差值更新。
|
图 6 改进PID算法流程图 |
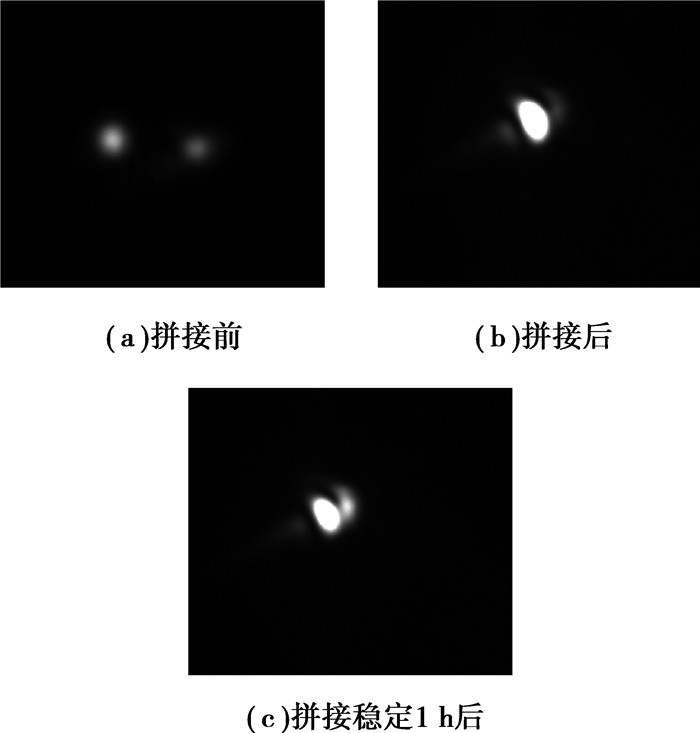
通过多次实验,改进的PID控制算法应用于拼接光栅自动闭环控制时,能够使拼接光栅系统实现高稳定性的特殊控制要求,实现光斑重合,而且重合时间长达1 h。图 7所示为实验中拼接光斑的图像。
|
图 7 拼接光栅实验光斑调整图 |
分析推导了拼接光栅的驱动器“L”型布置的四维误差调整的数学模型;对增量式PID算法进行“锁存补偿法”避免饱和遗失与“四点中心差分法”抗干扰的改进。改进的PID算法用于拼接光栅系统的自动闭环控制能够实现拼接光栅系统的动态稳定,而且稳定时间长达1 h。
| [1] | Perry M D, Mourou G. Terawatt to petawatt subpicosecond lasers[J]. Science, 1994, 264(5161): 917–924. DOI:10.1126/science.264.5161.917 |
| [2] |
左言磊, 魏晓峰, 朱启华, 等.
1700线/mm镀金光栅的拼接理论和实验研究[J]. 物理学报, 2007, 56(9): 5233–5236.
ZUO Yanlei, WEI Xiaofeng, ZHU Qihua, et al. Theoretical and experimental study of grating tiling[J]. Acta Physica Sinica, 2007, 56(9): 5233–5236. DOI:10.7498/aps.56.5233 (in Chinese) |
| [3] |
周忆, 廖云飞, 刘有海, 等.
大口径光栅拼接装置的微振动响应分析[J]. 重庆大学学报, 2012, 35(7): 49–53.
ZHOU Yi, LIAO Yunfei, LIU Youhai, et al. The micro-vibration analysis for the large aperture grating tiling device[J]. Journal of Chongqing University, 2012, 35(7): 49–53. DOI:10.11835/j.issn.1000-582X.2012.07.009 (in Chinese) |
| [4] | Bunkenburg J, Kessler T, Sskulski W, et al. Phase-locked control of tiling-grating assemblies for chirped-pulse-amplified lasers using a Mach-Zehnder interferometer[J]. Opt. Lett, 2006, 31(10): 1561–1563. DOI:10.1364/OL.31.001561 |
| [5] | Kessler T J, Bunkenburg J, Huang H, et al. Phase-locked control of tiling-grating assemblies for chirped-pulse-amplified lasers using a Mach-Zehnder interferometer[J]. Opt. Lett, 2004, 29: 635–637. DOI:10.1364/OL.29.000635 |
| [6] | Qiao J, Kalb A, Guardalben M J, King G, et al. Large-aperture grating tiling by interferometry for petawatt chirped-pulse-amplification systems[J]. Optics Express, 2007, 15(15): 9562–9574. DOI:10.1364/OE.15.009562 |
| [7] | Qiao J, Kalb A, Nguyen T, et al. Demonstration of large-aperture tiling-grating compressors for high-energy, petawatt-class, chirped-pulse amplification systems[J]. Opt. Lett, 2008, 33(15): 1684–1686. DOI:10.1364/OL.33.001684 |
| [8] | Cotel A, Casting M, Pichon P, et al. , Phased-array grating compression for high-energy chirped pulse amplification lasers[J]. Optics Express, 2007, 15(5): 2742–2752. DOI:10.1364/OE.15.002742 |
| [9] | Habara H, Guang X, Jitsuno T, et al. Pulse compression and beam focusing with segmented diffraction gratings in a high-power chirped-pulse amplification glass laser system[J]. Optics Letters, 2010, 35: 1783–1785. DOI:10.1364/OL.35.001783 |
| [10] |
绍忠喜, 张庆春, 白清顺, 等.
高精度大口径光栅拼接装置的控制算法[J]. 光学精密工程, 2009, 17(1): 158–165.
SHAO Zhongxi, ZHANG Qingchun, BAI Qingshun. Design method of controlling device for tiling high pecision and large aperture grating[J]. Opticis and Precision Engineering, 2009, 17(1): 158–165. (in Chinese) |
| [11] | Yang Y C, Wang X, Zhang J W, et a1. Automatic phase-locked control of grating tiling[J]. Optics and Lasers in Engineering, 2012, 50(2): 262–267. DOI:10.1016/j.optlaseng.2011.08.004 |
| [12] |
李绍铭, 刘寅虎.
基于改进型RBF神经网络多变量系统的PID控制[J]. 重庆大学学报:自然科学版, 2007, 30(2): 53–57.
LI Shaoming, LIU Yinghu. PID control for multivariable system based on ameliorative RBF neural networks[J]. Journal of Chongqing University:Natural Science Edition, 2007, 30(2): 53–57. (in Chinese) |
| [13] | Kaya I, Tan N, Atherton D P. A refinement procedure for PID controllers[J]. Electrical Engineering, 2006, 88: 215–221. DOI:10.1007/s00202-004-0276-9 |
| [14] | 王勇, 王聪瑜, 马雪梅, 等. 大口径拼接光栅的实现方案研究[C/OL]//第八届全国激光科学技术青年学术交流会论文集, 2005: 315-318. [2012-08-12]. http://www.docin.com/p-528476430.html |
| [15] |
赵博, 齐向东.
衍射光栅位相拼接的计算分析[J]. 光学技术, 2000, 26(5): 385–392.
ZHAO bo, QI Xiangdong. Analysis and computing for the phase matching of diffraction gratings[J]. Optical Technique, 2000, 26(5): 385–392. (in Chinese) |
| [16] |
张军伟, 陈伟, 周忆, 等.
压电驱动器位置布置对拼接光栅误差的影响[J]. 强激光与粒子束, 2012, 24(6): 1295–1300.
ZHANG Junwei, CHEN Wei, ZHOU Yi, et al. Effect of arrangement of piezoelectric actuators on grating tiling error[J]. High Power Laser and Particle Beams, 2012, 24(6): 1295–1300. (in Chinese) |
| [17] |
历风满.
数字PID控制算法的研究[J]. 辽宁大学学报, 2005, 32(4): 367–371.
LI Fengman. The research of controlling arithmetic for figure PID[J]. Journal of Liaoning University, 2005, 32(4): 367–371. (in Chinese) |
| [18] |
杨德刚, 姜磊, 贾文杰. 数字PID与其算法改进的研析[J]. 中国科技信息, 2010, 14: 102-105. YANG Degang, JIANG Lei, JIANG Wenjie[J].China Science and Technology Information, 2010, 14:102-105. |
 2013, Vol. 36
2013, Vol. 36


