2. 西北核技术研究所, 西安 710024
2. Northwest Institute of Nuclear Technology, Xi'an 710024, China
在传统的工程结构分析时,一般采用确定性的结构参数和数学模型。在所有的模型中,涉及结构的参数一般都是确定性的数值。所谓的确定性就是在计算中忽略了结构不稳定性而导致结构系统发生的变化,最终导致结构出现完全的不稳定性和计算误差。事实上,研究工程往往出现结构的不确定性[1],比如不同温度下各种材料性质的改变、物体的几何形状和尺寸在测量过程中产生的误差,结构在随机载荷下致外力随时间不断变化,一些结构涉及计算的初始条件和边界条件等。造成这些不确定性的原因有很多,有的是参数具有制造、安装误差等;有的是参数具有计算或测量误差;有的是系统在不同的工况下,参数具有不同的数值;有的是参数具有一定的变化区域或无法精确测定[2]。另外,还有与结构间接联系的一类不确定因素如工程需求等模糊因素。总之,实际结构中的误差或不确定性是普遍存在的。虽然,在很多情况下,这些误差和不确定性可能很小,但是由于累积就可能对结构造成很大的影响,尤其在比较复杂的结构中就更为明显。传统分析设计中,通过采用较大的安全系数来避免结构不确定性的影响,已经很难满足现代分析设计的要求[3]。因此研究工程中的不确定性的结构分析方法,具有重要的实际意义和理论价值。确定区间参数结构动力特性和静响应最值可以很好地解决某些结构不确定问题。
综上所述,给出区间参数结构动力特性和静响应的最值显得尤其重要,而寻求一种简单而有效的计算方法是必不可少的。区间参数结构的动力特性和静响应往往与参数之间存在着密切的联系[4-5],给出它们之间的内在联系可以使得区间参数结构动力特性和静响应的最值计算变得简单、有效。
1 区间参数弹模E和密度ρ的结构动力特性分析讨论区间参数弹性模量和质量密度的特征值响应:若结构第i个单元的弹性模量和质量密度的变化范围分别是
1) 在其他特性不变的情况下,若第i个单元的弹性模量增加,即Ei≥
| $ \frac{{\partial {\lambda _j}}}{{\partial {E_i}}} = \mathit{\boldsymbol{\varphi }}_j^{\rm{T}}\left( {\frac{{\partial \mathit{\boldsymbol{K}}}}{{\partial {E_i}}} - {\lambda _j}\frac{{\partial \mathit{\boldsymbol{M}}}}{{\partial {E_i}}}} \right){\varphi _j} = \mathit{\boldsymbol{\varphi }}_j^{\rm{T}}\frac{{\partial \mathit{\boldsymbol{K}}}}{{\partial {E_i}}}{\varphi _j} = \mathit{\boldsymbol{\varphi }}_j^{\rm{T}}\mathit{\boldsymbol{K}}_i^ * {\varphi _j}, $ | (1) |
因为Ki*为半正定对称矩阵,则φjTKi*φj≥0;φj∈Rn×1;
所以
2) 在其他特性不变的情况下,若第i个单元的质量密度增加,即ρi≥ρi0,又
| $ \begin{array}{*{20}{c}} {\frac{{\partial {\lambda _j}}}{{\partial {\rho _i}}} = \mathit{\boldsymbol{\varphi }}_j^{\rm{T}}\left( {\frac{{\partial \mathit{\boldsymbol{K}}}}{{\partial {\rho _i}}} - {\lambda _j}\frac{{\partial \mathit{\boldsymbol{M}}}}{{\partial {\rho _i}}}} \right){\varphi _j} = }\\ { - {\lambda _j}\mathit{\boldsymbol{\varphi }}_j^{\rm{T}}\frac{{\partial \mathit{\boldsymbol{M}}}}{{\partial {\rho _i}}}{\varphi _j} = - {\lambda _j}\mathit{\boldsymbol{\varphi }}_j^{\rm{T}}\mathit{\boldsymbol{M}}_i^ * {\varphi _j},} \end{array} $ | (2) |
同理,Mi为半正定对称矩阵;则φjTMi*φj≥0;则-λjφjTMi*φj≤0;φj∈Rn×1;所以
则λj≤λj0,j=1, 2, …,n。
综上所述,结论得以保证。
2 区间参数弹模E的结构静响应分析实际工程中,很多时候关心的是结构在力作用点位移的大小,而结构在单独一个力作用下,加载点位移取最值的参数取值具有特殊性[6],这里的加载点即力作用点,且方向同力的方向,推导如下。
讨论区间参数弹性模量的静力响应:当结构在某一个自由度方向被施加一个力(假设为正)时,结构各单元刚度(E)取最小值时,结构在该自由度方向的位移取最大值[7-8],反之,结构在该自由度方向的位移取最小值。
假定结构在k方向被施加一个力fk,则荷载向量F=[0;...fk; ...0], k方向位移δk>0,现求k方向位移δk对设计变量的灵敏度。
假设第n个单元的设计变量xn(E)发生变化,灵敏度为
由K×δ=F对设计变量xn求偏导得
| $ \frac{{\partial \mathit{\boldsymbol{K}}}}{{\partial {x_n}}}\delta + \mathit{\boldsymbol{K}}\frac{{\partial \delta }}{{\partial {x_n}}} = 0, $ | (3) |
| $ \mathit{\boldsymbol{K}}\frac{{\partial \delta }}{{\partial {x_n}}} = - \frac{{\partial \mathit{\boldsymbol{K}}}}{{\partial {x_n}}}\delta 。$ | (4) |
对于桁架或刚架,
| $ \begin{array}{l} \frac{{\partial \mathit{\boldsymbol{e}}{\mathit{\boldsymbol{k}}_n}}}{{\partial {x_n}}} = \left[ {\begin{array}{*{20}{c}} {{k_{2i - 1,2i - 1}}}&{{k_{2i - 1,2i}}}&{{k_{2i - 1,2j - 1}}}&{{k_{2i - 1,2j}}}\\ {{k_{2i,2i - 1}}}&{{k_{2i,2i}}}&{{k_{2i,2j - 1}}}&{{k_{2i,2j}}}\\ {{k_{2j - 1,2i - 1}}}&{{k_{2j - 1,2i}}}&{{k_{2j - 1,2j - 1}}}&{{k_{2j - 1,2j}}}\\ {{k_{2j,2i - 1}}}&{{k_{2j,2i}}}&{{k_{2j,2j - 1}}}&{{k_{2j,2j}}} \end{array}} \right],\\ \frac{{\partial \mathit{\boldsymbol{K}}}}{{\partial {x_n}}} = \left[ {\begin{array}{*{20}{c}} 0& \cdots &{}&{}&{}&{}&{}&{}&{}\\ \vdots&\ddots &{}&{}&{}&{}&{}&{}&{}\\ {}&{}&{{k_{2i - 1,2i - 1}}}&{{k_{2i - 1,2i}}}& \cdots &{{k_{2i - 1,2j - 1}}}&{{k_{2i - 1,2j}}}&{}&{}\\ {}&{}&{{k_{2i,2i - 1}}}&{{k_{2i,2i}}}& \cdots &{{k_{2i,2j - 1}}}&{{k_{2i,2j}}}&{}&{}\\ {}&{}& \vdots&\vdots&\ddots&\vdots&\vdots &{}&{}\\ {}&{}&{{k_{2j - 1,2i - 1}}}&{{k_{2j - 1,2i}}}& \cdots &{{k_{2j - 1,2j - 1}}}&{{k_{2j - 1,2j}}}&{}&{}\\ {}&{}&{{k_{2j,2i - 1}}}&{{k_{2j,2i}}}& \cdots &{{k_{2j,2j - 1}}}&{{k_{2j,2j}}}&{}&{}\\ {}&{}&{}&{}&{}&{}&{}& \ddots&\vdots \\ {}&{}&{}&{}&{}&{}&{}& \cdots &0 \end{array}} \right],\\ \frac{{\partial \mathit{\boldsymbol{K}}}}{{\partial {x_n}}}\delta = \left[ {\begin{array}{*{20}{c}} 0\\ \vdots \\ {\sum\limits_m {{k_{2i - 1,m}}{\delta _m}} }\\ {\sum\limits_m {{k_{2i,m}}{\delta _m}} }\\ \vdots \\ {\sum\limits_m {{k_{2j - 1,m}}{\delta _m}} }\\ {\sum\limits_m {{k_{2j,m}}{\delta _m}} }\\ \vdots \\ 0 \end{array}} \right],m = 2i - 1,2i,2j - 1,2j, \end{array} $ | (5) |
将式(5)带入式(4)得式(6)
| $ \mathit{\boldsymbol{K}}\frac{{\partial \delta }}{{\partial {x_n}}} = - \left[ {\begin{array}{*{20}{c}} 0\\ \vdots \\ {\sum\limits_m {{k_{2i - 1,m}}{\delta _m}} }\\ {\sum\limits_m {{k_{2i,m}}{\delta _m}} }\\ \vdots \\ {\sum\limits_m {{k_{2j - 1,m}}{\delta _m}} }\\ {\sum\limits_m {{k_{2j,m}}{\delta _m}} }\\ \vdots \\ 0 \end{array}} \right],m = 2i - 1,2i,2j - 1,2j, $ | (6) |
由式(6)可知,
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{K}}\frac{{\partial \delta }}{{\partial {x_n}}} = \left[ {\begin{array}{*{20}{c}} 0\\ M\\ {\sum\limits_m {{k_{2i - 1,m}}{\delta _m}} }\\ M\\ M\\ M\\ M\\ M\\ 0 \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} 0\\ M\\ M\\ {\sum\limits_m {{k_{2i,m}}{\delta _m}} }\\ M\\ M\\ M\\ M\\ 0 \end{array}} \right] - }\\ {\left[ {\begin{array}{*{20}{c}} 0\\ M\\ M\\ M\\ M\\ {\sum\limits_m {{k_{2j - 1,m}}{\delta _m}} }\\ M\\ M\\ 0 \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} 0\\ M\\ M\\ M\\ M\\ M\\ {\sum\limits_m {{k_{2j,m}}{\delta _m}} }\\ M\\ 0 \end{array}} \right],}\\ {m = 2i - 1,2i,2j - 1,2j。} \end{array} $ | (7) |
则灵敏度
| $ {f_k}{\left( {\frac{{\partial {\delta _k}}}{{\partial {x_n}}}} \right)_{2i - 1}} = \left( { - \sum\limits_m {{k_{2i - 1,m}}{\delta _m}} } \right){\delta _{2i - 1}}; $ |
| $ {\left( {\frac{{\partial {\delta _k}}}{{\partial {x_n}}}} \right)_{2i - 1}} = - \frac{1}{{{f_k}}}\left( {\sum\limits_m {{k_{2i - 1,m}}{\delta _m}} } \right){\delta _{2i - 1}}; $ |
同理得
| $ \begin{array}{*{20}{c}} {{{\left( {\frac{{\partial {\delta _k}}}{{\partial {x_n}}}} \right)}_{2i}} = - \frac{1}{{{f_k}}}\left( {\sum\limits_m {{k_{2i,m}}{\delta _m}} } \right){\delta _{2i}};{{\left( {\frac{{\partial {\delta _k}}}{{\partial {x_n}}}} \right)}_{2j - 1}} = }\\ { - \frac{1}{{{f_k}}}\left( {\sum\limits_m {{k_{2j - 1,m}}{\delta _m}} } \right){\delta _{2j - 1}};}\\ {{{\left( {\frac{{\partial {\delta _k}}}{{\partial {x_n}}}} \right)}_{2j}} = - \frac{1}{{{f_k}}}\left( {\sum\limits_m {{k_{2i,m}}{\delta _m}} } \right){\delta _{2j}};}\\ {\frac{{\partial {\delta _k}}}{{\partial {x_n}}} = \sum\limits_m {{{\left( {\frac{{\partial {\delta _k}}}{{\partial {x_n}}}} \right)}_m}} = - \frac{1}{{{f_k}}}{{\left( {{\delta ^ * }} \right)}^{\rm{T}}}\frac{{\partial \mathit{\boldsymbol{e}}{\mathit{\boldsymbol{k}}_n}}}{{\partial {x_n}}}{\delta ^ * },} \end{array} $ | (8) |
| $ {\delta ^ * } = \left[ {\begin{array}{*{20}{c}} {{\delta _{2i - 1}};}&{{\delta _{2i}};}&{{\delta _{2j - 1}};}&{{\delta _{2j}}} \end{array}} \right] $ |
由单元刚度矩阵的正定性知
| $ \delta _k^l > \delta _k^{l - 1};l = 1,2,3 \cdots n $ |
综上所述,结论得以保证。
3 分析结果对于区间参数弹模E和质量密度ρ,从理论上推导了特征值取最值时,相应的区间参数取值;对于区间参数弹模E,推导了单工况加载点位移取最值时,相应的区间参数取值。并得出3个结论:
1) 对于弹模E,当E取最大值时,特征值取最大值;反之,特征值取最小值。
2) 对于密度ρ,当ρ取最小值时,特征值取最大值;反之,特征值取最小值。
3) 对于弹模E,在单工况加载情况下,当E取最小值时,加载点方向位移取最大值;反之,加载点方向位移取最小值[9]。
4 算例对于桁架,单元刚度矩阵ek和单元质量em矩阵都是A的线性表达式[10-12],则第i个单元刚度矩阵和单元质量矩阵对Ai的灵敏度为
| $ \frac{{\partial \mathit{\boldsymbol{e}}{\mathit{\boldsymbol{k}}_i}}}{{\partial {A_i}}} = \frac{{\mathit{\boldsymbol{e}}{\mathit{\boldsymbol{k}}_i}}}{{{A_i}}};\frac{{\partial \mathit{\boldsymbol{e}}{\mathit{\boldsymbol{m}}_i}}}{{\partial {A_i}}} = \frac{{\mathit{\boldsymbol{e}}{\mathit{\boldsymbol{m}}_i}}}{{{A_i}}}。$ | (9) |
则总体刚度矩阵K和总体质量矩阵M对Ai的灵敏度
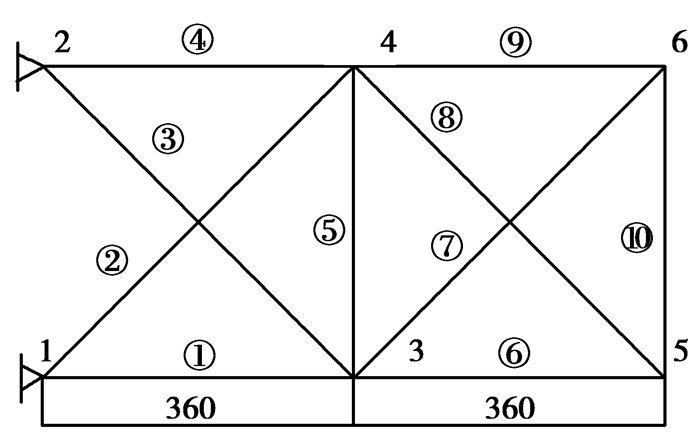
算例:图 1为十杆平面桁架,弹性模量E=2.1e11 Pa,密度ρ=7.8e3 kg/m3,以各杆的横截面积为设计变量,求第一阶特征值的最大值和最小值。
|
图 1 十杆平面桁架 |
1) 给定小参数区间
As=[5.01 5.01 5.01 5.01 5.01 5.01 5.01 5.01 5.01 5.01];
Al=[5.21 5.21 5.21 5.21 5.21 5.21 5.21 5.21 5.21 5.21];
初始设计变量取
A0=[5.15 5.15 5.15 5.15 5.15 5.15 5.15 5.15 5.15 5.15];
上述公式计算结果见表 1。
| 表 1 小参数区间的第一阶特征值优化结果 |
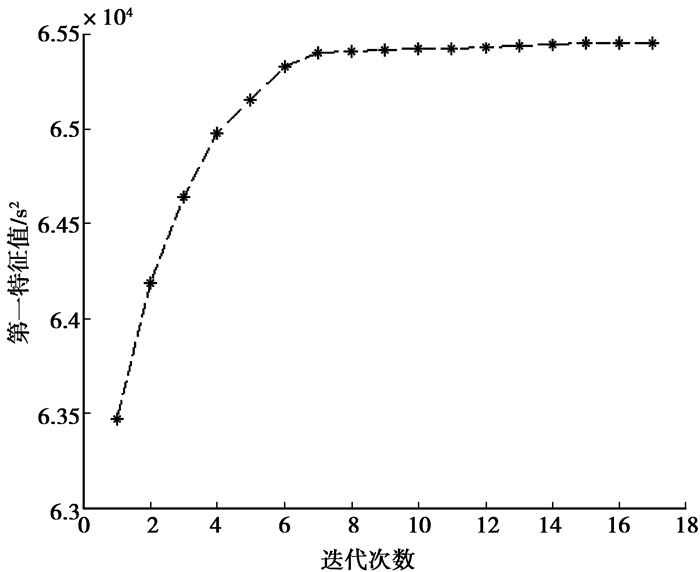
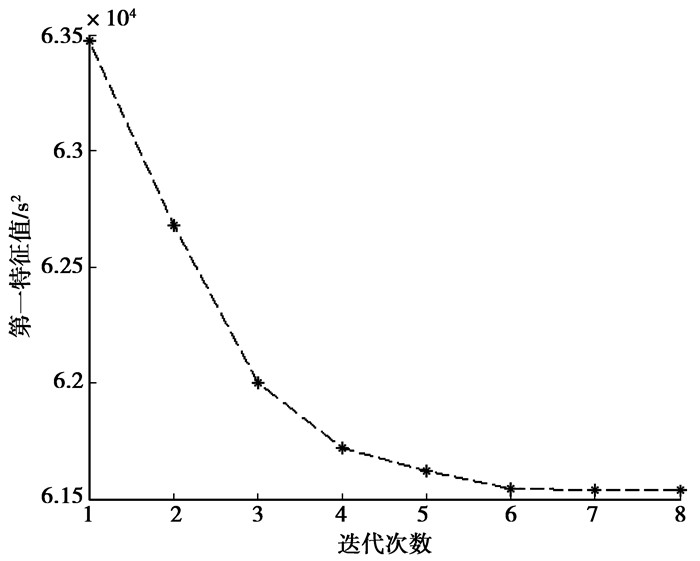
由表 1可以看出,对于每一根杆,当结构的第一阶特征值在这根杆面积最大处取最大值时,那么它在这根杆面积最小处取最小值;同时,当结构的第一阶特征值在这根杆面积最大处取最小值时,那么它在这根杆面积最小处取最大值。这是由于结构参数小区间不确定性,即灵敏度在此小范围内不变号,那么目标函数为每个设计变量的单调函数,因此,目标函数在边界处取得最值,且最小值对应的面积和最大值对应的面积是相对的[13-15],目标函数最大值和最小值见图 2和图 3。
|
图 2 第一阶特征值的最大值 |
|
图 3 第一阶特征值的最小值 |
|
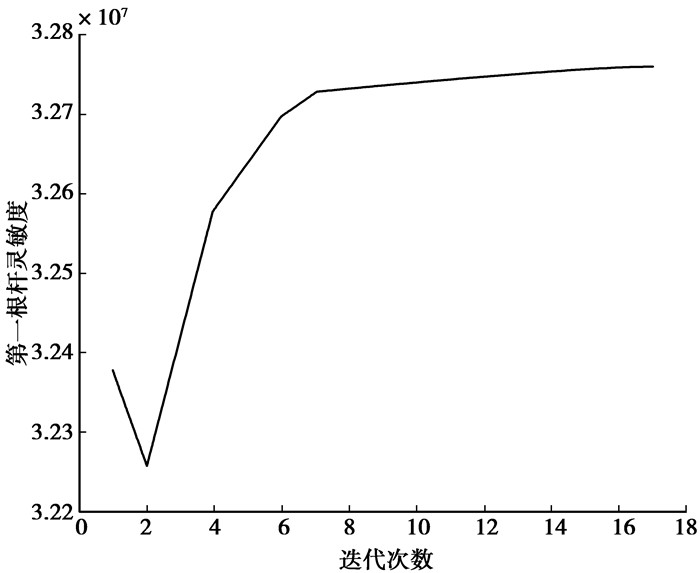
图 4 特征值最大值的灵敏度 |
|
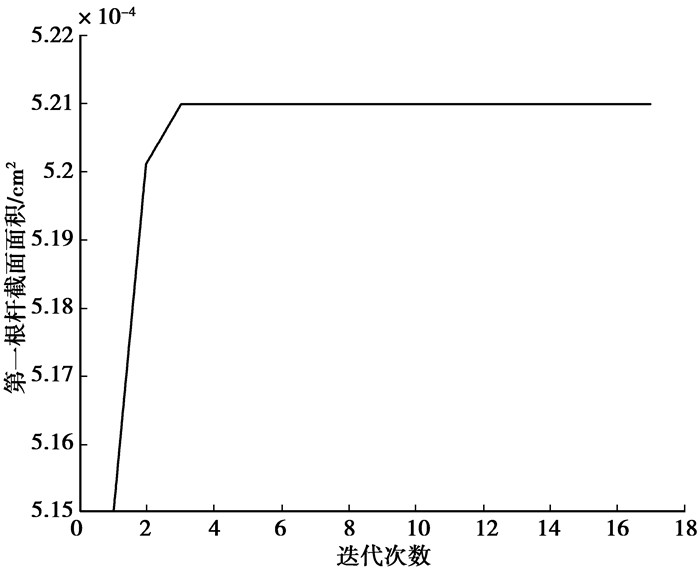
图 5 特征值最大值的面积 |
|
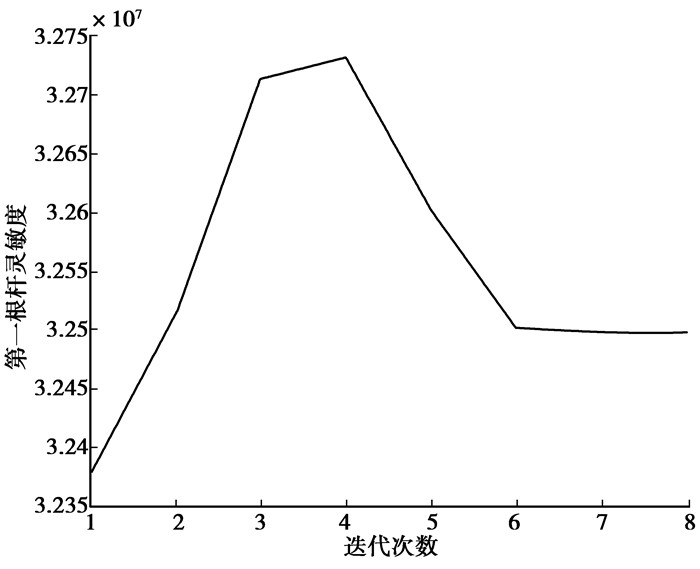
图 6 特征值最小值的灵敏度 |
|
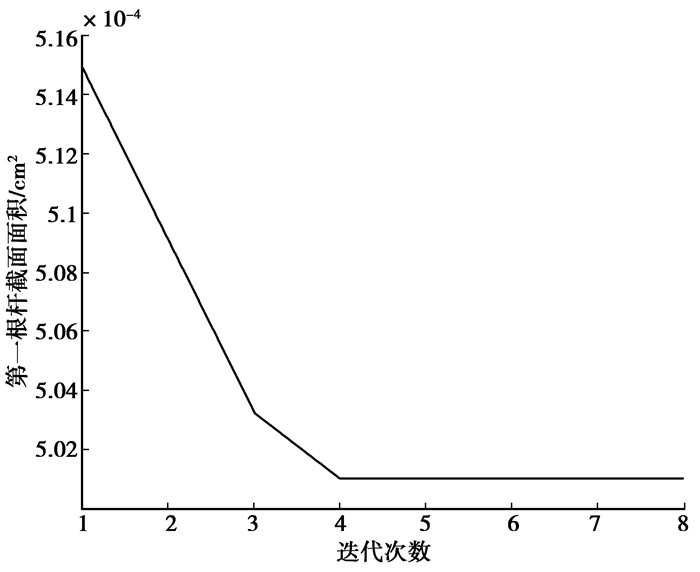
图 7 特征值最小值的面积 |
2) 给定大参数区间
As=[1 1 1 1 1 1 1 1 1 1];
Al=[60 60 60 60 60 60 60 60 60 60];
初始设计变量取
A0=[30 30 30 30 30 30 30 30 30 30];
上述公式计算结果见表 2。
| 表 2 大参数区间的第一阶特征值优化结果 |
在表 2中,当特征值取最大值时,有些杆的面积不再取边界值,这说明灵敏度在某一情况下发生了变化,但对于该参数区间,特征值取最小值时,各个杆的面积仍然取边界值,特征值最大值和最小值见图 8和9。
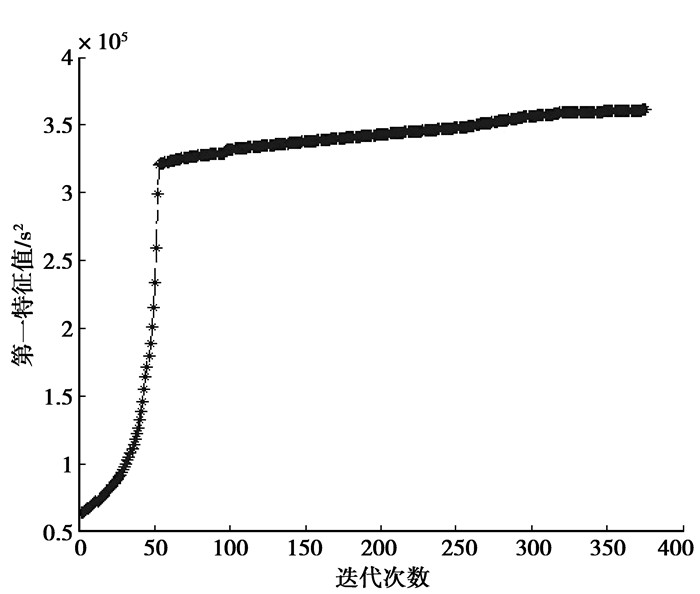
|
图 8 第一阶特征值的最大值 |
|
图 9 第一阶特征值的最小值 |
|
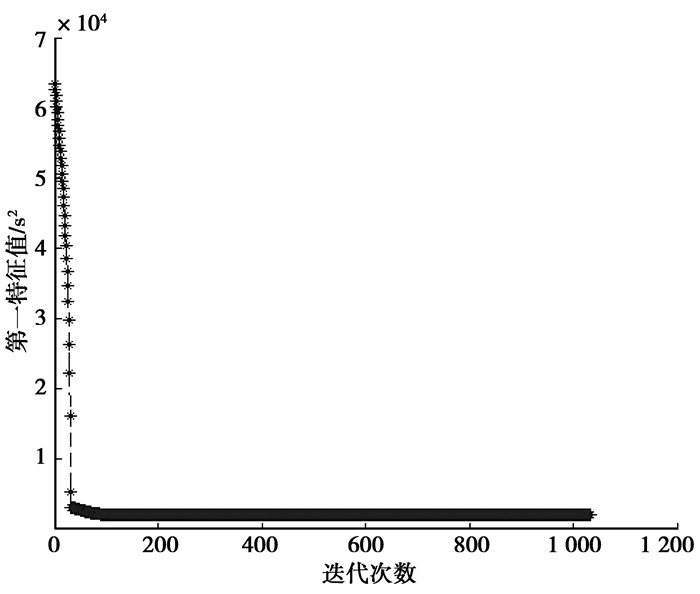
图 10 特征值最大值的灵敏度 |
|
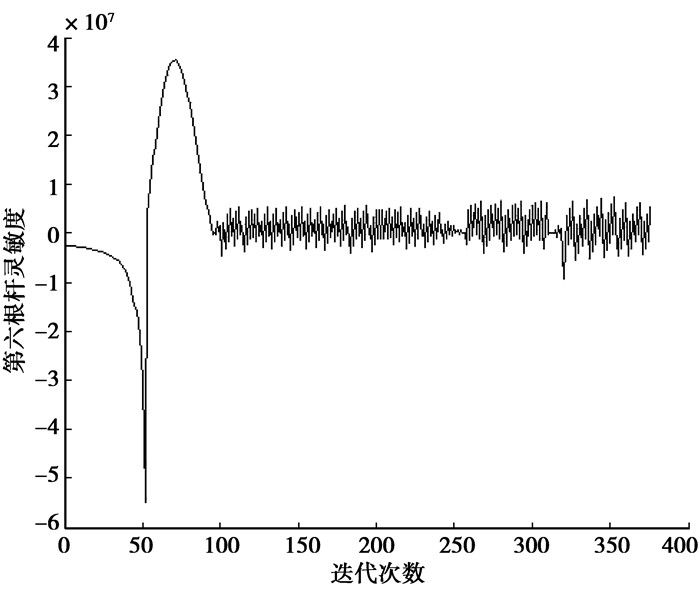
图 11 特征值最大值的面积 |
|
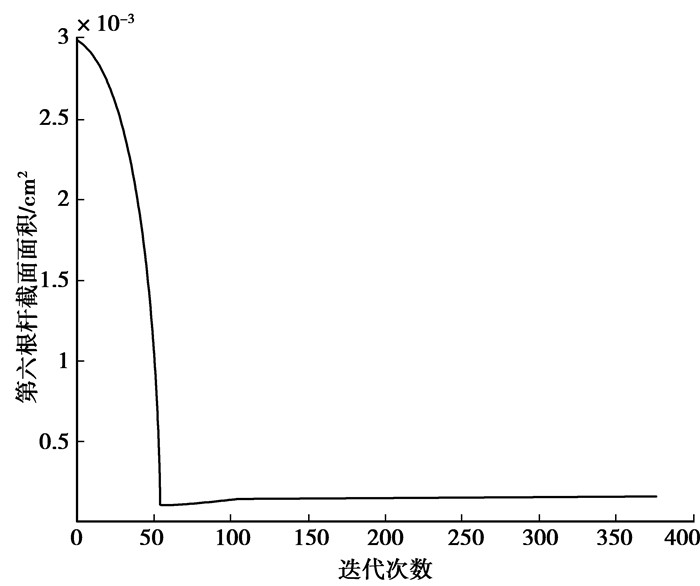
图 12 特征值最小值的灵敏度 |
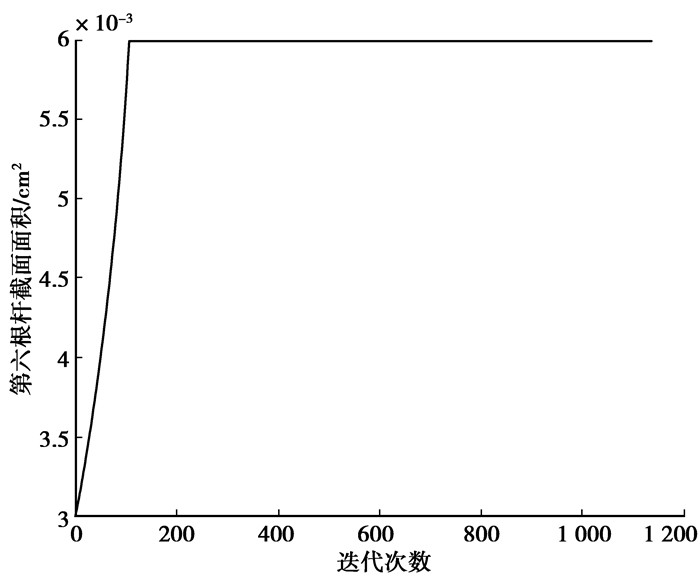
|
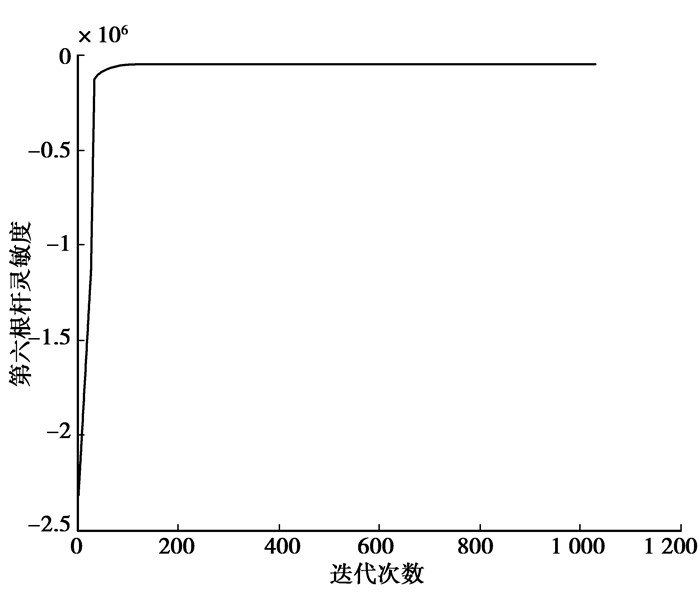
图 13 特征值最小值的面积 |
由图 10~图 13可以看出,对于最大值,灵敏度最后在0的位置上下波动,面积最后收敛到一个非边界值;对于最小值,灵敏度一直为负,面积最后收敛到边界值。
5 结束语以面积A为设计参数,讨论了桁架对于区间参数A的特征值最值和位移最值计算。对于特征值最值,用小区间和大区间分别计算了特征值最值的参数取值,并从所得到的结果分析了计算的正确性。同时,分别计算了单工况荷载作用下,加载点方向和非加载点方向的位移最值,比较了它们的参数取值,并验证了弹性模量E与加载点方向位移的关系。
| [1] | Yakov B H, Isaac E. Convex models of uncertainty in applied mechanics[M]. Amsterdam: Elsevier Science Publishers, 1990. |
| [2] | Hien T D, Kleiber M. Finite element analysis based on stochastic Hamilton variation principle[J]. Computer&Structures, 1990, 37(6): 893–902. |
| [3] | Markow S. An iterative method for algebraic solution to interval equations[J]. Applied Numerical Mathematics, 1999, 30(2/3): 225–239. |
| [4] | Qiu Z P, Chen S H, Elishakoff I. Natural frequencies of structures with uncertain but non-random parameters[J]. Journal of Optimization Theory and Applications, 1995, 86(3): 669–683. DOI:10.1007/BF02192164 |
| [5] | Chen S H, Qiu Z P, Song D T. A new method for computing the upper and lower bounds on frequencies of structures with interval parameters[J]. Mechanics Research Communication, 1994, 21(6): 583–592. DOI:10.1016/0093-6413(94)90021-3 |
| [6] |
刘先斌, 陈虬, 陈大鹏.
非线性随机动力系统的稳定性和分岔研究[J]. 力学进展, 1996, 26(4): 437–452.
LIU Xianbin, CHEN Qiu, Chen Dapeng. The researches on the stability an bifurcation of nonlinear stochastic dynamical systems[J]. Advances in Mechanics, 1996, 26(4): 437–452. DOI:10.6052/1000-0992-1996-4-J1996-041 (in Chinese) |
| [7] |
刘扬, 程耿东.
关于结构模糊优化若干间题的讨论[J]. 计算结构力学及其应用, 1989, 6(3): 61–66.
LIU Yang, CHENG Gengdong. Discussion on fuzzy optimal design of structure[J]. Computational structural, Mechanics and Applications, 1989, 6(3): 61–66. (in Chinese) |
| [8] | 王彩华. 工程结构模糊优化设计[M]. 重庆: 重庆大学出版社, 1986. |
| [9] |
郭书祥, 吕震宙.
线性区间有限元静力控制方程的组合解法[J]. 计算力学学报, 2003, 20(1): 34–38.
GUO Shuxiang, Lü Zhenzhou. Advanced combinatorial methods for solving the governing equations of linear static interval finite element method[J]. Chinese Journal of Computational Mechanics, 2003, 20(1): 34–38. (in Chinese) |
| [10] | 陈塑寰. 随机参数结构的振动理论[M]. 长春: 吉林科学技术出版社, 1992. |
| [11] | 朱位秋. 随机振动[M]. 北京: 科学出版社, 1992. |
| [12] |
雷鹏, 苏怀智, 张贵金.
基于RNN模型的坝体和岩基区间参数反演方法研究[J]. 岩土力学, 2011, 32(2): 547–552.
LEI Peng, SU Huaizhi, ZHANG Guijing. Study of interval parameters back analysis of dam body and rock foundation based on RNN model[J]. Rock and Soil Mechanics, 2011, 32(2): 547–552. (in Chinese) |
| [13] |
宋宗凤, 陈建军, 刘国梁.
随机-区间参数平面连续体结构可靠性分析[J]. 武汉理工大学学报, 2010, 32(8): 125–129.
SONG Zongfeng, CHEN Jianjun, LIU Guoliang. Reliability analysis of random-interval parameters planar continuum structures[J]. Journal of Wuhan University of Technology, 2010, 32(8): 125–129. (in Chinese) |
| [14] |
王敏娟, 陈建军, 林立广, 等.
区间参数智能梁结构闭环系统动态特性分析[J]. 电子科技大学学报, 2011, 40(1): 152–156.
WANG Minjuan, CHEN Jianjun, LIN Liguang, et al. Dynamic characteristic analysis of closed loop systems for the intelligent beam with interval parameters[J]. Journal of University of Electronic Science and Technology of China, 2011, 40(1): 152–156. (in Chinese) |
| [15] |
刘立平, 杨实君, 李英民.
软夹层参数对边坡动力特性的影响分析[J]. 重庆大学学报:自然科学版, 2007, 30(5): 31–34.
LIU Liping, YANG Shijun, LI Yingmin. Influence of soft soil layer on dynamic characteristic of the slope[J]. Journal of Chongqing University:Natural Science Edition, 2007, 30(5): 31–34. (in Chinese) |
 2013, Vol. 36
2013, Vol. 36


