b. 重庆大学 建设管理与房地产学院, 重庆 400045
b. College of Construction Management and Real Estate, Chongqing University, Chongqing 400045, China
对土木结构进行实时安全监测或振动控制,不仅需要掌握结构的静力特性,更需要充分了解其动力特性,以避免灾难事故的发生。而结构的模态参数(频率、阻尼、振型)是结构动力特性的主要参数,所以如何准确识别结构的模态参数是研究结构动力特性的基础[1-3]。
数据驱动随机子空间法(SSI)的识别精度高,但计算效率较低[4-5]。由于运用ITD、STD、复指数法进行参数识别时必须先进行随机减量法或者自然激励技术(NExT法)得到数据的自由衰减曲线,而此过程会产生一定的误差,且这2种前处理方法的输出长度的取值有一定的人为主观影响,有时也会使得衰减曲线产生偏差,在此情况下采用ITD、STD、复指数法进行参数识别必然会产生误差[6-7]。数据驱动SSI中Hankel矩阵经过正交投影计算保留了原始数据中的所有信息,同时去除了噪声,因此将得到的P矩阵中的数据来作为ITD、STD、复指数法的输入数据,3种方法就不再需要进行随机减量法或者自然激励技术(NExT法)前处理,避免了这2种前处理方法的不准确性带来的误差。结合随机子空间法精度较高但计算效率较低与ITD、STD、复指数法精度较低但计算效率较高的特点,提出了3种改进的模态参数识别方法,即改进ITD法、改进STD法和改进复指数法。
1 改进ITD法数据驱动随机子空间法是先构造Hankel矩阵,然后进行矩阵的正交投影得到Pi矩阵,将其展开得:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}_i} = {Y_f}/{Y_p} = {O_i}{{\hat X}_i} = }\\ {\left[{\begin{array}{*{20}{c}} C\\ {CA}\\ \vdots \\ {C{A^{i-1}}} \end{array}} \right]\left[{\begin{array}{*{20}{c}} {{{\hat x}_i}}&{{{\hat x}_{i + 1}}}& \cdots &{{{\hat x}_{i + j-1}}} \end{array}} \right] = }\\ {\left[{\begin{array}{*{20}{c}} {C{{\hat x}_i}}&{C{{\hat x}_{i + 1}}}& \cdots &{C{{\hat x}_{i + j-1}}}\\ {CA{{\hat x}_i}}&{CA{{\hat x}_{i + 1}}}& \cdots &{CA{{\hat x}_{i + 1}}}\\ \vdots&\vdots &{}& \vdots \\ {C{A^{i-1}}{{\hat x}_i}}&{C{A^{i-1}}{{\hat x}_{i + 1}}}& \cdots &{C{A^{i - 1}}{{\hat x}_{i + j - 1}}} \end{array}} \right]。} \end{array} $ | (1) |
将得到的P矩阵中的数据来作为ITD法的输入数据。注意到Pi的第m行恰好可以看作是其第m-1的延时Δt的矩阵。这也是ITD法的原理所在:不妨把第一行到第m行看作响应矩阵[X],其中0 < m < i(i是Pi矩阵的行数),第二行到第m+1行看作第一行的延时Δt的矩阵[X],用Matlab语言表述如下:
| $ \left[\mathit{\boldsymbol{X}} \right] = {P_i}\left( {1:m, :} \right);\left[{\bar X} \right] = {P_i}\left( {2:m + 1, :} \right), $ | (2) |
两者相除后:
| $ \left[\mathit{\boldsymbol{X}} \right]\backslash \left[{\mathit{\boldsymbol{\bar X}}} \right] = \left[\mathit{\boldsymbol{A}} \right]。$ | (3) |
将矩阵[A]采用双最小二乘解方法,此种方法实际上就是2种单边最小二乘法的平均值,即:
| $ \begin{array}{*{20}{c}} {\left[\mathit{\boldsymbol{A}} \right] = \frac{1}{2}\left[{\left[{\mathit{\boldsymbol{\bar X}}} \right]{{\left[\mathit{\boldsymbol{X}} \right]}^{\rm{T}}}{{\left( {\left[\mathit{\boldsymbol{X}} \right]{{\left[\mathit{\boldsymbol{X}} \right]}^{\rm{T}}}} \right)}^{ - 1}} + } \right.}\\ {\left. {\left[{\mathit{\boldsymbol{\bar X}}} \right]{{\left[{\mathit{\boldsymbol{\bar X}}} \right]}^{\rm{T}}}{{\left( {\left[\mathit{\boldsymbol{X}} \right]{{\left[{\mathit{\boldsymbol{\bar X}}} \right]}^{\rm{T}}}} \right)}^{ -1}}} \right]。} \end{array} $ | (4) |
式(4)正是ITD法所要求解的特征矩阵[A]。余下的过程与一般的ITD法相同[8]。
2 改进STD法将得到的P矩阵中的数据作为STD法的输入数据,形成STD法中的Hessenberg矩阵,提高了识别精度和抗噪性能。同样定义随机子空间法式(1)所示Pi第1行到第m行看作响应矩阵[X],其中0 < m < i(i是Pi矩阵的行数),第2行到第m+1行看作第一行的延时Δt的矩阵[X]。
由式(2),同样可以得出[X]和[X]存在线性关系,即
| $ \left[{\mathit{\boldsymbol{\bar X}}} \right] = \left[\mathit{\boldsymbol{X}} \right]\left[\mathit{\boldsymbol{B}} \right]。$ | (5) |
矩阵[B]具有如下的形式:
| $ \left[\mathit{\boldsymbol{B}} \right] = \left[{\begin{array}{*{20}{c}} {0, 0, 0, \cdots, 0, {b_1}}\\ {1, 0, 0, \cdots, 0, {b_2}}\\ {0, 1, 0, \cdots, 0, {b_3}}\\ \vdots \\ {0, 0, 0, \cdots, 1, {b_M}} \end{array}} \right], $ | (6) |
[B]矩阵是1个只有1列位置元素的Hessenberg矩阵。
| $ \left[\mathit{\boldsymbol{X}} \right]\left\{ b \right\} = {\left\{ {\bar x} \right\}_M}, $ | (7) |
其中:{b}=[b1, b2, b3, ..., b2N]T;而{x}M是矩阵[X]的第M列元素。
用最小二乘法求解{b}矩阵后可得
| $ \left\{ b \right\} = {\left( {\left[\mathit{\boldsymbol{X}} \right]{{\left[\mathit{\boldsymbol{X}} \right]}^{\rm{T}}}} \right)^{ - 1}}{\left[\mathit{\boldsymbol{X}} \right]^{\rm{T}}}{\left\{ {\bar x} \right\}_M}, $ | (8) |
将求得的{b}代入后,得到[B],将式(7)代入式(6)整理后得
| $ \left[\mathit{\boldsymbol{B}} \right]{\left[\mathit{\boldsymbol{ \boldsymbol{\varLambda} }} \right]^{ - 1}} = {\left[\mathit{\boldsymbol{ \boldsymbol{\varLambda} }} \right]^{ - 1}}\left[\alpha \right]。$ | (9) |
式(9)是一个标准的特征方程。由矩阵[B]的特征值esrΔt(r=1, 2, …, 2N),从而求出模态频率和阻尼比等模态参数[9]。
3 改进复指数法将得到的Pi矩阵中的数据作为复指数法的输入数据,即将随机子空间法中式(1)所示Pi的第1行单独提出来,即:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}_i}{{\left( {:, 1} \right)}^{\rm{T}}} = \left[{\begin{array}{*{20}{c}} {C{{\hat x}_i}}&{CA{{\hat x}_i}}& \cdots &{C{A^{i-1}}{{\hat x}_i}} \end{array}} \right]}\\ { = \left[{\begin{array}{*{20}{c}} {{j_0}}&{{j_1}}& \cdots &{{j_k}} \end{array}} \right], } \end{array} $ | (10) |
式中:
根据式(10),将状态矩阵A进行特征值分解:
| $ \mathit{\boldsymbol{A}} = \mathit{\Psi \Lambda }{\mathit{\Psi }^{ - 1}}, $ | (11) |
式中Λ=diag[μi]∈Rn×n是一个对角矩阵,由离散时间复特征值μi组成,Ψ∈Rn×n是以特征向量为列向量组成的矩阵。
将式(11)代入式(10)可以得到
| $ \begin{array}{l} {P_i}{\left( {1, :} \right)^{\rm{T}}} = \left[{\begin{array}{*{20}{c}} {{j_0}}&{{j_1}}& \cdots &{{j_k}} \end{array}} \right] = \\ \;\;\;\;\;\;\;\;\;\;\;\left[{\begin{array}{*{20}{c}} {C{{\hat x}_i}}&{C\mathit{\Psi \Lambda }{\mathit{\Psi }^{-1}}{{\hat x}_i}}& \cdots &{C\mathit{\Psi }{\mathit{\Lambda }^{i-1}}{\mathit{\Psi }^{-1}}{{\hat x}_i}} \end{array}} \right]。\end{array} $ | (12) |
写成方程组的形式:
| $ \left. \begin{array}{l} {j_0} = C{{\hat x}_i}\\ {j_1} = C\mathit{\Psi }\left[{\begin{array}{*{20}{c}} {{\mu _1}}&{}&0\\ {}& \ddots &{}\\ 0&{}&{{\mu _{2N}}} \end{array}} \right]{\mathit{\Psi }^{ - 1}}{{\hat x}_i}\\ {j_2} = C\mathit{\Psi }\left[{\begin{array}{*{20}{c}} {\mu _1^2}&{}&0\\ {}& \ddots &{}\\ 0&{}&{\mu _{2N}^2} \end{array}} \right]{\mathit{\Psi }^{ - 1}}{{\hat x}_i}\\ \vdots \\ {j_{i - 1}} = C\mathit{\Psi }\left[{\begin{array}{*{20}{c}} {\mu _1^{i-1}}&{}&0\\ {}& \ddots &{}\\ 0&{}&{\mu _{2N}^{i-1}} \end{array}} \right]{\mathit{\Psi }^{ - 1}}{{\hat x}_i} \end{array} \right\}。$ | (13) |
对于上式jk是已知的,最主要是求μr(r=1, 2, …, 2N),可以将μr看做是一个具有实系数βk(自回归系数)的2N阶的多项式方程的根,即:
| $ \sum\limits_{k = 0}^{2N} {{\beta _k}{\mu ^k}} = \prod\limits_{r = 1}^N {\left( {\mu - {\mu _r}} \right)\left( {\mu - \mu _r^ * } \right)} = 0。$ | (14) |
余下的过程与一般的复指数法相同[10]。
4 框架结构模态辨识实验地震激励可以看作环境激励中的一种,现用前面提到的3种改进的模态参数识别方法对同济大学土木工程防灾国家重点实验室12层钢筋混凝土框架结构振动台模型试验进行模态参数识别,以此来验证这些改进方法的正确性、可行性。
4.1 振动台试验介绍 4.1.1 模型介绍钢筋混凝土标准框架振动台模型试验于2003年6月在同济大学土木工程防灾国家重点实验室振动台试验室进行。试验模型如图 1所示,模型共12层,缩尺比为1:10,梁、柱、板的尺寸由实际高层框架结构的尺寸按相似关系折算。详尽的模型设计参数、材料特性、模型制作过程等可以参考其试验报告[11]。

|
图 1 试验模型图 |
试验中采用加速度计、应变传感器量测模型结构的动力响应。加速度计的方向有X、Y、Z 3个方向。试验测点布置如图 2所示。
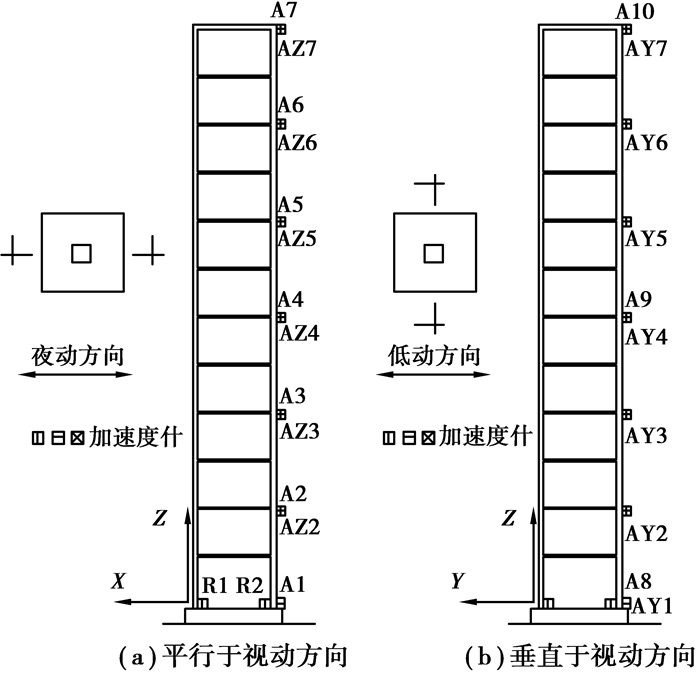
|
图 2 模型测点布置 |
试验中输入的地震波形有El Centro波、Kobe波、上海人工波及上海基岩波。该试验共设62个工况,其中8次白噪声输入,28次X方向的单向地震动输入,14次XY双向输入,12次XYZ三向输入。更加详细的资料请参见其试验报告[11]。
4.1.4 测得的加速度时程针对每1个工况,每1个传感器都记录下这个工况的对应位置的时程曲线。例如第2工况A1、A2测得加速度时程如图 3、图 4所示。结构振动台模型试验过程可以发现,前7个工况下(相当于原型体系遭受七度多遇地震),在模型结构上没有发现任何裂缝。这说明直到第7个工况完成为止,结构一直处于强震动段前的非时变阶段。为了避开时变阶段,在此选取前7个工况中的数据来进行模态参数识别。
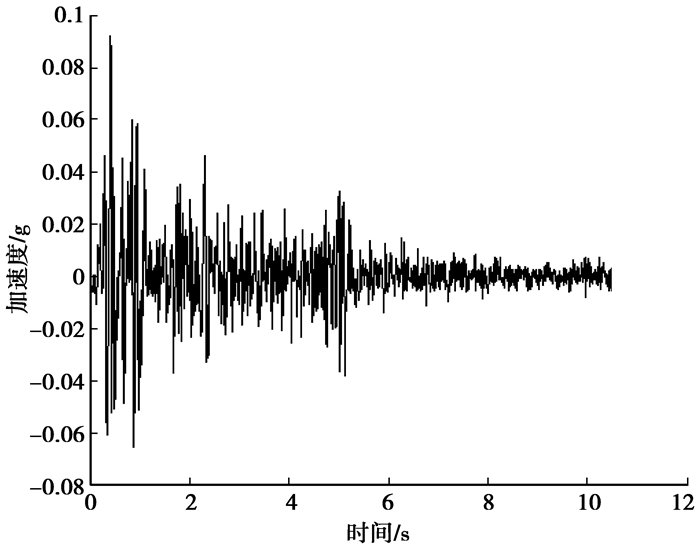
|
图 3 工况2A1加速度时程 |
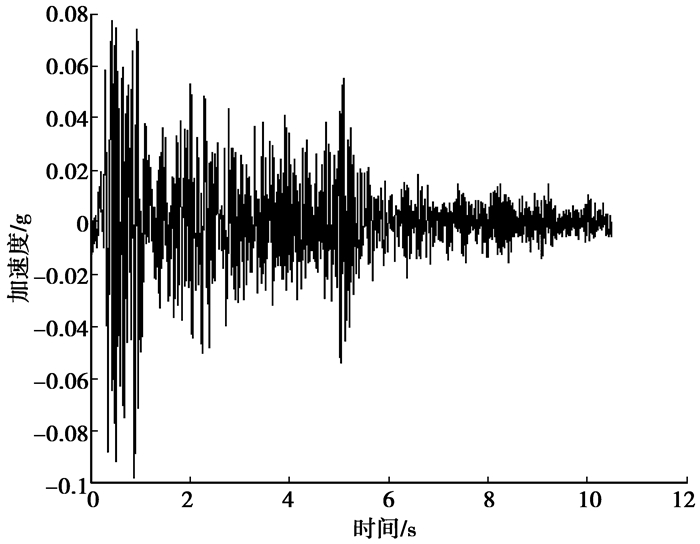
|
图 4 工况2A2加速度时程 |
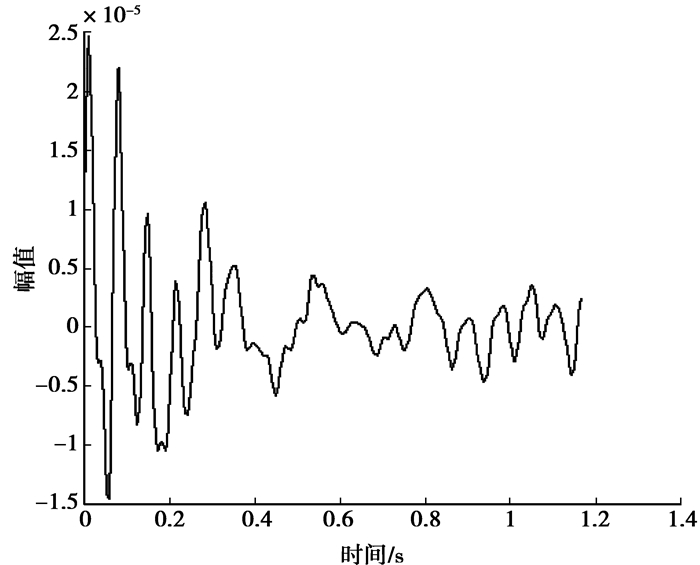
现以工况2数据作为研究对象。工况2是El-Centro波单X向输入,取X向A1-A7测点所得数据作为响应数据输入。用NExt法对这些数据做预处理,以A1测点为参考点,分别用A2~A7测点数据对其做互相关函数,其结果为6条互相关曲线。其中A2与A1、A3与A1互相关函数曲线如图 5、图 6所示。
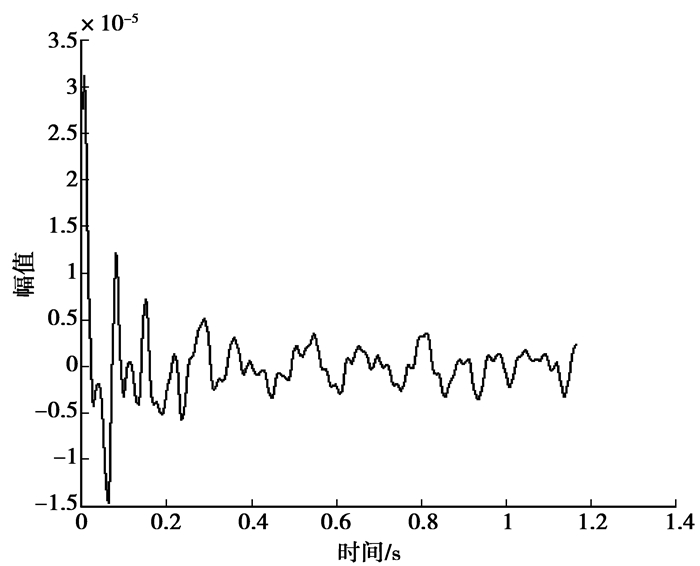
|
图 5 A2、A1互相关函数曲线 |
|
图 6 A3、A1互相关函数曲线 |
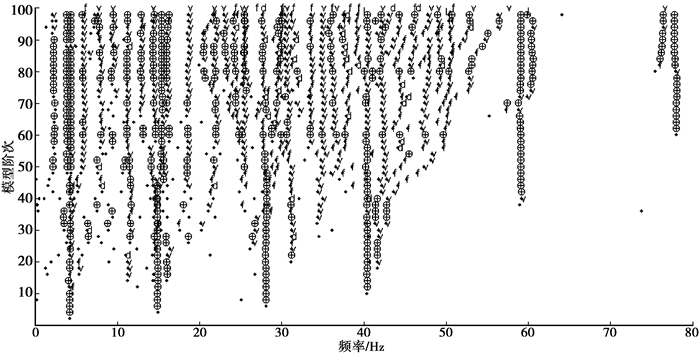
以A1~A7数据作为输入数据,选取合适的Hankel矩阵行数后,分别取模型阶次由2变换至100,然后做出其稳定图。取频率容差为1%,阻尼比容差为10%,模态振型容差为5%,得到如图 7所示的稳定图。
|
图 7 稳定图 |
由稳定图可以明显看出其前六阶稳定轴,以此剔除虚假模态,识别结果如表 1、表 2。同时通过构造Hankel矩阵,对其进行正交投影计算,得到P矩阵,然后取其中若干行或者列的数据作为ITD、STD、复指数法的输入数据来进行模态参数识别,识别结果如表 1、表 2所示。
| 表 1 3种改进方法的频率识别值的比较 |
| 表 2 3种改进方法的阻尼比识别值的比较 |
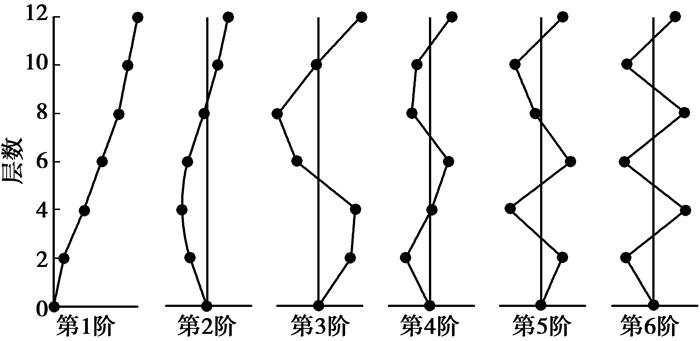
由识别结果可以看出,频率识别结果较接近,而对阻尼比识别的精度相对较差。由于篇幅原因,现只给出改进ITD法对该框架结构的振型识别结果,如图 8所示。
|
图 8 改进ITD法振型识别 |
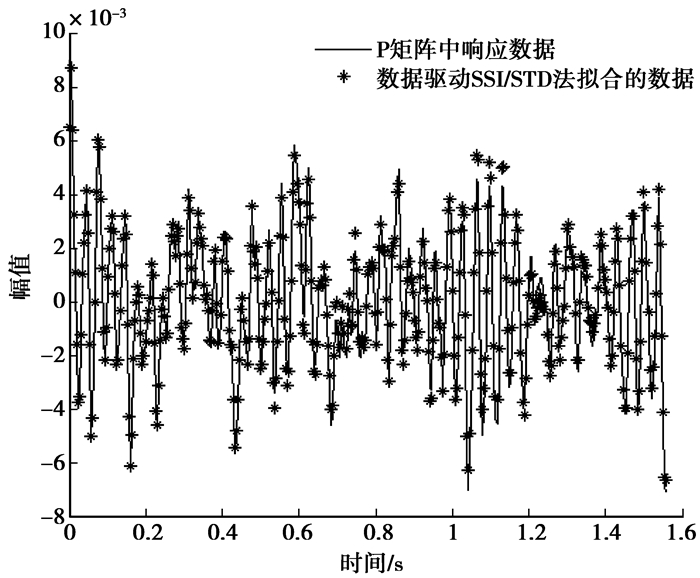
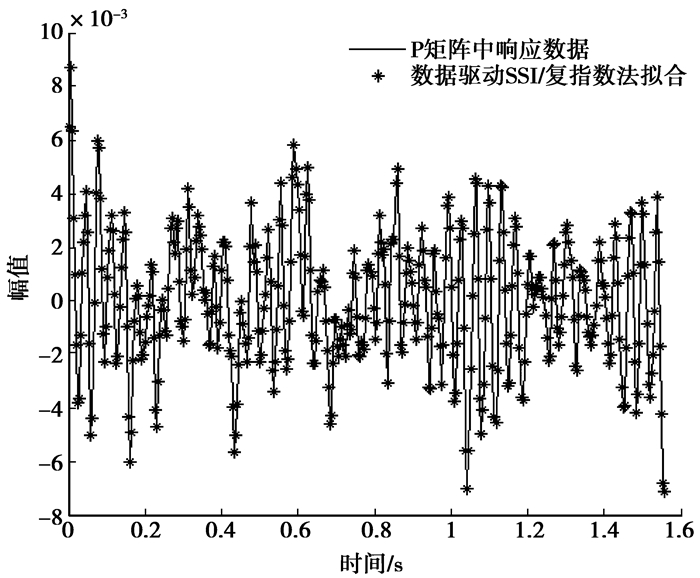
通过分析得到的模态参数反推输入数据,所得到的拟合值与原始输入数据如图 9、图 10所示。
|
图 9 改进STD法拟合情况 |
|
图 10 改进复指数法拟合情况 |
由图 9与图 10可以看出:所得拟合值与原始输入数据情况拟合较好,从而进一步证明3种改进方法在结构模态参数识别中应用的可行性。
5 结论1) 运用ITD、STD和复指数法进行参数识别时必须先采用随机减量法或者自然激励技术(NExT法)得到数据的自由衰减曲线,而此过程会产生一定的误差,且这2种前处理方法的输出长度的取值方面有一定的人为主观影响,有时也会使得衰减曲线产生偏差,因此采用ITD、STD和复指数法进行参数识别必然会产生误差。
2) 结合随机子空间算法识别精度高和ITD、STD和复指数法的识别效率高,提出了环境激励下结构模态参数识别的改进ITD、改进STD和改进复指数法。通过十二层钢筋混凝土标准框架振动台模型试验验证了改进方法对模态参数识别的可行性,与一般方法相比,改进方法明显提高了对频率和阻尼比等结构模态参数的识别精度。
3) 用求得的振型矩阵反推原始数据,所得的拟合数据与原始相应数据拟合度非常高,从而进一步证明了改进方法识别模态参数的准确性和识别方法的正确性。
| [1] | Juang J N. Applied system identification[M]. Londen: Prentice-Hall, 1994. |
| [2] | Huang C F, Ko W J, Tal C H. Identification of dynamic systems from data composed by combination of their response components[J]. Engineering Structures, 2002, 24(11): 1441–1450. DOI:10.1016/S0141-0296(02)00092-5 |
| [3] | Ren W X, Zong Z H. Output-only modal parameter identification of civil engineering structures[J]. Structural Engineering and Mechanics, 2004, 17(3/4): 429–444. |
| [4] | Koh C G, Hong B, Llaw C Y. Substructural and progressive structural identification methods[J]. Engineering Structures, 2003, 25(12): 1551–1563. DOI:10.1016/S0141-0296(03)00122-6 |
| [5] | 崔飞. 桥梁结构参数识别及承载力分析[D]. 上海: 同济大学, 2003. |
| [6] |
韩建平, 李达文, 王飞行.
基于Hilbert-Huang变换和随机子空间识别的模态参数识别[J]. 地震工程与工程振动, 2010, 30(1): 53–59.
HAN Jianping, LI Dawen, WANG Feixing. Modal parameter identification based on Hilbert-Huang transform and stochastic subspace identification[J]. Journal of Earthquake Engineering and Engineering Vibration, 2010, 30(1): 53–59. (in Chinese) |
| [7] |
徐晓霞, 任伟新, 韩建刚.
基于响应协方差小波变换和SVD的结构工作模态参数识别[J]. 振动工程学报, 2010, 23(2): 194–199.
XU Xiaoxia, REN Weixin, HAN Jiangang. Operational modal parameter identification based on covariancedriven wavelet transform and singular value decomposition[J]. Journal of Vibration Engineering, 2010, 23(2): 194–199. (in Chinese) |
| [8] | Peng Z K, Tse P W, Chu F L. An improved Hilbert-Huang transform and its application in vibration signal analysis[J]. Journal of Sound and Vibration, 2005, 286(1/2): 187–205. |
| [9] | Ren W X, Zong Z H. Output-only modal parameter identification of civil engineering structures[J]. Structural Engineering and Mechanics, 2004, 17(3/4): 429–444. |
| [10] | 李海龙. 环境激励下结构模态参数识别方法研究[D]. 重庆: 重庆大学, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10611-1012048741.htm |
| [11] | 吕西林, 李培振, 陈跃庆. 12层钢筋混凝土标准框架振动台模型试验的完整数据[R]. 上海: 同济大学, 2004. |
 2013, Vol. 36
2013, Vol. 36


