2. 西南大学 政治与公共管理学院, 重庆 400700;
3. 中国移动通信集团 重庆有限公司, 重庆 401121
2. School of Political Science and Public Administration, Southwest University, Chongqing 400700, China;
3. Chongqing Branch of China Mobile, Chongqing 401121, China
农村信息化是社会信息化的一部分,是通讯技术和计算机技术在农村生产、生活和社会管理中实现普遍应用和推广的过程[1]。它不仅包括农业信息技术,还涉及微电子技术、通信技术、光电技术等在农村生产、生活、管理等方面普遍而系统的应用过程。
随着中国第三代移动通信技术的发展,以中国自主知识产权为核心的时分同步码分多址(TD-SCDMA)技术,已被国际上广泛接受和认可,成为第三代无线通信的国际标准[2]。目前,中国正大力推动TD-SCDMA技术在农村信息化中的普及和应用,利用其在频谱利用率、频率灵活性、业务支持多样性及成本控制等方面有独特优势,解决目前农村信息化中存在信息“到不了、不好用、不好找、用不起”的突出问题[3]。
当然,由于时分双工方式自身的特点,TD-SCDMA在网络下载速度、可允许终端移动速度等方面落后于频分双工方式。因此,最大限度减少各种农村信息化应用中传输、处理、存储的数据量,成为最为有效的避免TD-SCDMA技术劣势的解决手段[4-5]。
为此,作者以TD-SCDMA网络中占有极大比重的多媒体数据为研究切入点,提出一种多媒体数据并行管理框架。该框架改进了多媒体数据管理中典型的顺序执行方式,实现了数据产生和数据分析的并行处理,不仅有效降低了对数据传输带宽的要求,而且易于并行优化。论文以农村信息化建设中图像分析的实际应用,阐述了该并行管理框架的设计实现方式。
1 多媒体数据并行管理框架在第三代移动通信网络中,数据管理通常是指由原始数据获取到标准数据产生以及分析,直至结果输出的完整过程,有时还涉及中间的传输及存储环节。其中,原始数据是通过各种传感器获取的未经预处理和标准化转换的数据,标准数据则是依据被广泛接受的特定协议所产生的数据。常规的数据管理往往是通过顺序方式执行的,其框架如图 1(a)所示。
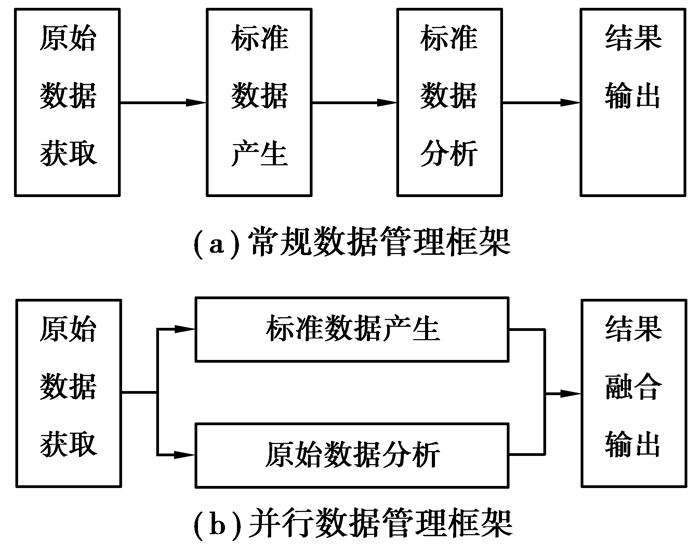
|
图 1 数据管理框架 |
随着计算机技术的发展,当前处理器(包含嵌入式系统处理器)的发展呈现出多核化趋势,计算处理单元的核心数目由单个扩展为2个、4个甚至8个以上,同时,关于数字信号处理和并行处理的多媒体加速指令也逐渐出现在新一代多媒体指令集中[6]。但是,单核频率的提升并不突出,摩尔定律逐渐失效。因此,顺序执行的常规数据管理框架,必然成为性能优化和效率提升的瓶颈。为了适应当前处理器和多媒体指令集的发展趋势,必须将标准数据的产生过程与数据的分析过程并行化。通过并行方式优化的数据管理框架如图 1(b)所示。
需要注意的是,数据管理并行化并非处理步骤的简单搬移。在常规数据管理框架中,数据分析是针对标准化后的数据,以图像数据为例,图像分析是针对BMP、JPEG等格式的标准化数字图像。假若并行优化,执行图像分析操作时标准化的数字图像尚未生成。因此,数据分析算法可适应未经标准化的数据,是进行多媒体数据并行管理框架优化设计的基础和关键。
2 图像分析应用实例多媒体数据种类繁多,处理方式不一。结合图像数据管理应用,对多媒体数据的并行管理优化设计方法进行介绍。
2.1 数字图像生成过程分析为了实现图像数据的并行管理,需要对图像数据的生成过程进行拆解,以寻找未经标准化的原始数据。
数字图像的生成是根据人类视觉感官将光电器件传感信号转换为灰度或彩色信息的过程[7],核心步骤为解马赛克过程(Demosaicking),通常包含对原始信息的饱和度、锐利度、对比度进行的必要调整,以及为了适合传播所进行的编码压缩。在这期间,原数据中诸多细节信息被忽略而无法重现,导致图像局部特征显著性降低。因此,可以说数字图像的生成本质上是为了便于人类“观看”,而并非最适合机器去“分析”[8]。
在数字图像生成过程中产生的表征图像传感器上每个感光单元积聚电荷多少(即反映照射到感光单元上光线强度)的原数据(RAW Data),由于未经数字图像生成阶段解马赛克过程的插值处理,以及对饱和度、锐利度、对比度的调整,相比于JPEG等有损压缩的标准化图像格式,能够最大限度地保留场景的最真实信息[9]。同时,由于原数据中每一像素位置只记录单个颜色通道的信息,因此原数据的数据量则仅为相同图像尺寸未经压缩的标准化图像格式(如BMP、TIFF等)的数据量的1/3。
2.2 图像数据的并行管理框架设计原数据由于数据量相对较小,细节信息丰富,且便于后续并行处理,所以适合作为并行优化的起点。以图像分析中基础的配准应用为例,其并行管理框架可设计为如图 2的形式。
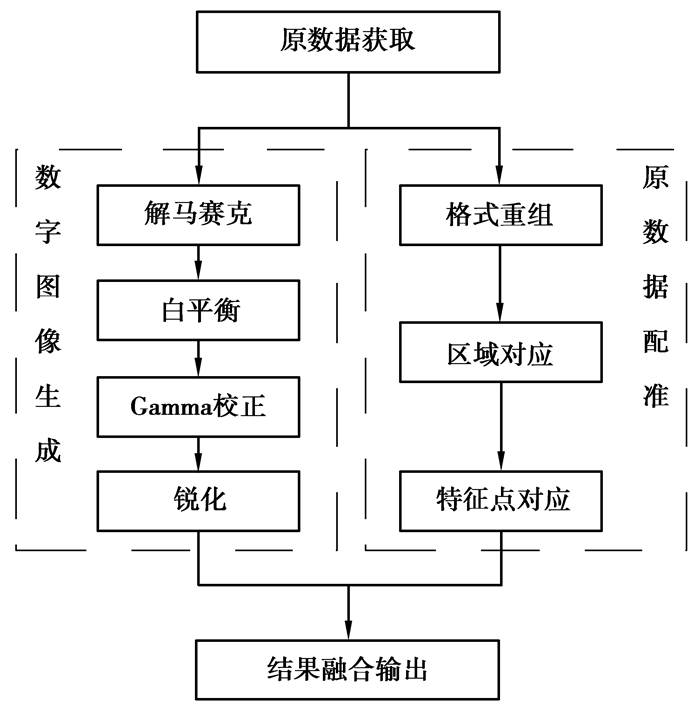
|
图 2 图像配准的并行管理优化 |
依旧以图像分析中基础的配准应用为例进行阐述。相比于标准化图像的分析方法,原数据分析算法设计需要在图像分析方法基础上结合原数据自身的排列组合形式重新设计。
图 3为典型的Bayer Pattern原数据结构示意图,每个像素点位置仅存储一个通道的颜色,其中R代表红色分量、G代表绿色分量、B代表蓝色分量。根据光度测量理论,人类视网膜对于绿色光敏感[10],因此原数据中绿色成分比其他两种颜色的数量要多1倍。

|
图 3 原数据的数据结构 |
根据原数据的数据结构,通过简单地亮度计算即可格式重组得到1/2降采样的单通道亮度图像。相比通过解马赛克生成的BMP图像,上述处理得到的亮度图像的数据量仅为BMP图像的1/12。
接下来,采用作者提出的二步式快速图像配准方法进行图像分析[11]。该方法主要包含区域对应和特征点对应两个主要阶段。在区域对应阶段,对两幅图像分别获取具有较高独特性和不变性的特征区域并进行匹配,得到这些特征区域之间的对应关系。进入特征点对应阶段后,利用一种轻量级的特征检测算子在已建立对应关系的特征区域上检测特征点,并采用一种紧凑的16维描述符进行描述,最后采用混合溢出树(Spill Tree)算法[12]查找对应,获取对应特征点的精确定位。
由于在第二阶段的实现过程中,算法对尺度、光照、对比度和旋转变化产生的影响进行了针对性的处理,同时,第二阶段的特征点检测是约束在已建立对应关系的特征区域中,而这区域本身具有良好的仿射不变性,因此,该算法在理论上对仿射和尺度变化均具有较强的鲁棒性。
得益于由粗到精的二步式框架,进行特征区域检测的目的不再是得到尽可能多的特征区域,进而得到尽可能多的对应关系,而仅仅是得到约束第二阶段特征点对应的区域。换句话说,在特征区域检测阶段,只需要考虑如何对图像进行合适的分割,并建立分割后特征区域的对应关系。这种特征区域不需要考虑嵌套现象,而只需要寻找满足一定面积约束条件的面积相对最大的稳定区域。因此,在第一阶段,特征描述和匹配的运算量极大减少。另外,由于在第二阶段所采用的特征点检测算法被限制在已建立对应关系并且规范化后的特征区域中,因此描述符维度也可以减少,进一步减少了运算量。
首先介绍区域对应阶段的实现方式。区域对应阶段的主要任务是获取2幅图像的特征区域,并建立这些特征区域之间的对应关系。由于第二阶段的特征点精确定位约束在这些对应区域中,因此,区域对应的准确性和覆盖面直接影响了算法的整体性能。
对于二步式配准方法,一个较为理想的特征区域需要具备以下特征:
1) 在各种视觉条件变化下(如尺度、光照、视角偏移等)均具有较好的独特性和鉴别力。
2) 特征区域之间应尽量避免重叠和嵌套,以减少特征区域描述与匹配以及特征点对应阶段的冗余计算。
3) 特征区域的势(即像素数)应在一定的约束范围内,这是因为之后的特征点对应阶段采用了一种轻量级的局部特征配准算法,当区域的势大于一定阈值时,匹配的精确性显著下降。
4) 特征区域应尽可能覆盖整个图像。
区域对应阶段的特征区域分割,采用受到光子成像原理启发的像素差异度量法。众所周知,图像传感器的实质是光子计数器。根据成像原理,当大量的光子投射到传感器靶面的时候,其成像后某一像素点的图像噪声服从泊松分布,并且通常可以近似为高斯分布[13]。假定μ为亮度期望,那么观测亮度I的概率可以定义为
| $ P\left( {I/\mu } \right) = G\left( {\mu, \sqrt {a\mu } } \right), $ | (1) |
其中a为相机增益,其作用是将光子数量转换为像素值。为了简化模型,将a设置为1。那么,图像中某个像素点P比另一像素点Q具有较大均值的概率为
| $ \begin{gathered} P\left( {\mu \left( P \right) > \mu \left( Q \right)} \right) = 1-\mathit{\Phi }\left( {-\frac{{\mu \left( P \right)-\mu \left( Q \right)}}{{\sqrt {\mu \left( P \right) + \mu \left( Q \right)} }}} \right) = \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\Phi }\left( {\frac{{\mu \left( P \right) - \mu \left( Q \right)}}{{\sqrt {\mu \left( P \right) + \mu \left( Q \right)} }}} \right), \hfill \\ \end{gathered} $ | (2) |
其中,Φ为标准正态分布的积累分布函数。因为Φ从0到1单调增长,所以它的参数的绝对值可以用来作为边缘显著的一种度量。由于μ(P)和μ(Q)可以被替换为它们的最大似然估计I(P)和I(Q)。因此,边缘显著性d可以表示为
| $ d = \frac{{\left| {\mu \left( P \right)-\mu \left( Q \right)} \right|}}{{\sqrt {\mu \left( P \right) + \mu \left( Q \right)} }} = \frac{{\left| {I\left( P \right)-I\left( Q \right)} \right|}}{{\sqrt {I\left( P \right) + I\left( Q \right)} }}。$ | (3) |
在实际中,以d作为区域增长的度量时,区域增长是非线性的,通常在开始阶段增长速度很快,而在后期变化很慢。为了使图像的进化过程近似正比于时间步长t的变化,引入对积累分布函数的逆变换过程,可得到
| $ c\left( x \right) = P\left( {d < x} \right) = \frac{2}{{\sqrt {\rm{ \mathsf{ π} }} }}\int_0^{\sqrt {x/\lambda } } {{e^{-{y^2}}}} {\rm{d}}y, $ | (4) |
于是,在时间步长t时,距离阈值可构造为
| $ {d_{{\rm{thr}}}}\left( t \right) = {c^{- 1}}\left( {t/T} \right)\;\;t \in \left[{0, T} \right] $ | (5) |
其中T为所有的时间步长数,通常设置为200。
通过增长时间步长t,可以得到一系列的连通区域。在这个增长过程中,每个连通区域C(t)的势和它的距离阈值dthr(t)都将被记录。定义在时间步长t处的膨胀率为
| $ {r_t} = \frac{{C\left( {t + \Delta } \right)-C\left( t \right)}}{{{d_{{\rm{thr}}}}\left( {t + \Delta } \right)-{d_{{\rm{thr}}}}\left( t \right)}}, $ | (6) |
其中,Δ为时间增量。具有较小膨胀率的区域被定义为特征区域,即特征区域是在相对较大的距离阈值变化下,却保持相对较小的面积变化的区域。
检测到的特征区域必然存在嵌套现象。在实现中,对重叠面积超过80%的区域进行剔除,并对特征区域的势进行约束。经上述操作,一幅800×600像素图像的特征区域数量通常在80个以内。
为了便于对形状不规则且尺寸不统一的特征区域进行统一的描述和匹配,选取其外接拟合椭圆所包围的整个区域进行变换。之后,将椭圆区域规范为统一的尺寸,并采用尺度不变特征转换(SIFT)描述符[14]和混合溢出树方法分别进行描述和检索。
完成区域对应后,即进入特征点对应阶段。为了产生足够数量的局部特征点,当前的检测算法倾向于通过直接比较周围像素点的亮度关系来定位特征点。这是因为SIFT等经典算法,为了得到更好的重复率,使提取的图像特征能够有效抑制二阶作用的影响,通常引入一些具有针对性的处理过程。但是这些操作,只有在极端测试环境下(例如大范围视角偏移等),其作用才能真正体现,而在常规的测试环境中(例如尺度、旋转、小范围光照变化等),不仅导致了运算量的增加,也影响了算法的鲁棒性。基于上述分析,在本阶段的特征点检测部分,仅对候选点周围离散圆上16个像素点的强度进行考察。
在进行特征点检测之前,首先将已建立了对应关系的特征区域调整为同样的尺寸,以提高算法对尺度变化的鲁棒性。
在椭圆区域中的离散圆上,若至少n个连续像素的亮度均大于(负极性)或者小于(正极性)中心点亮度一定程度,则该中心点为特征点(如图 4所示)。根据实验,在n取12时得到最好的性能。当n取值小于12时,有可能定位到边缘;相反,当n取值大于12时,准则又过于苛刻,从而把一些较显著的局部特征滤除。在多数情况下,仅仅判断几个像素点便可将非特征点滤除。

|
图 4 特征点定位 |
当特征点定位后,对离散圆上每相邻的3个像素点的亮度求和,共同组成一个低维描述符。假定Ri是离散圆R上的一个像素点,Ricw和Riccw表示其在圆上顺时针和逆时针方向相邻位置的像素点,则其对应于描述符D上的元素可被表述为
| $ {D_i} = 0.5 \times {I_{{R_{icw}}}} + {I_{{R_i}}} + 0.5 \times {I_{{R_{iccw}}}}, $ | (7) |
其中,i∈[1, 16]。实验证明,这比直接采用单像素点的亮度构建描述符元素更加稳定。进一步采用圆上像素点到圆心的亮度梯度G来代替其亮度I,以便抑制弱光照变化的影响,于是Di可表述为
| $ {D_i} = 0.5 \times {G_{{R_{icw}} \to P}} + {G_{{R_i} \to P}} + 0.5 \times {G_{{R_{iccw}} \to P}}, $ | (8) |
其中,i∈[1, 16]。
选择最显著和(即Di的最大值)作为描述符的第一维度,然后按照顺时针方向依次填充描述符向量。如果最显著和不止一个,则所有可能的描述符都将被单独保留。这种简单的操作不仅使对特征点的描述与图像的二维旋转无关,更重要的是,它减少了计算描述符朝向的运算开销。为了抑制对比度的变化,还需要对描述符进行归一化处理。在实际中,每个特征点的极性也被记录,因为在进行检索时利用它们进行最初的二分类非常有效。
最后,所有的描述符都被存储于一个列表中,并以描述符上所有元素的绝对值之和来表征其显著性。众所周知,一个区域上特征点的数量依赖于图像的内容,纹理变化丰富的区域通常可以检测到较多的特征点。为了使特征点的分布更加均匀,根据显著性排序,并按照一定的密度(不高于12像素每点)选取区域中待匹配的特征点。
在最后的匹配部分,采用混合溢出树方法进行对应特征的检索,并采用RANSAC方法去除错误匹配[15]。
2.4 图像并行管理优化实验为了验证提出的多媒体数据并行管理框架的性能,作者将并行优化后的二步式图像配准方法与SIFT算法和GLOH[16]算法进行对比分析。
首先采用对应特征数目和重建相似度2个评估指标测试算法精度[17],测试图像选自牛津大学仿射协变特征图像测试库[18]。所有测试图像的尺寸在实验前被统一规范化为800×600像素。图 5显示了对“Graffiti”序列进行实验的结果,其中图 5(a)图显示了对应点数随着视角变化的曲线,图 5(b)显示了重建相似度随着视角变化的曲线。可以看出,无论是对应特征数目还是重建相似度,与SIFT和GLOH算法相比,并行优化后的二步式快速图像配准算法在较小的旋转和视角变化下,性能并有未显著的损失,在较大的视角偏移下性能更加接近。同时,研究方法执行一次配准操作所需的时间仅为0.311 s,相当于SIFT算法(1.972 s)的15.77%,以及GLOH算法(2.087 s)的14.90%。实验的硬件平台为配置为2.7 GHz Intel Core i5 CPU和4 GB RAM的笔记本电脑。
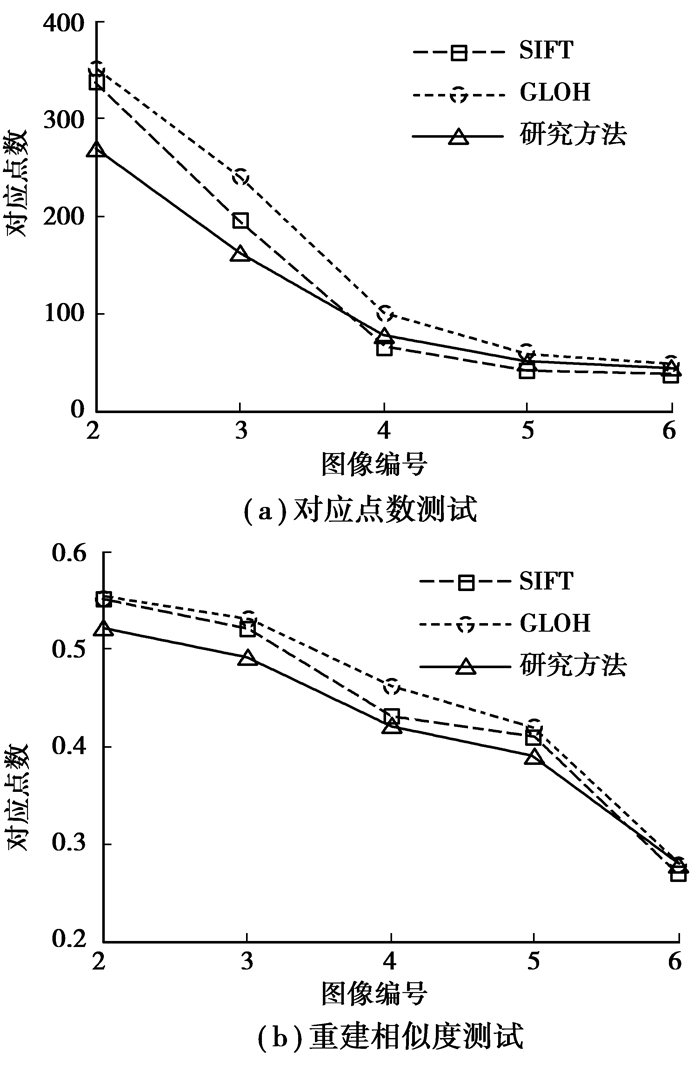
|
图 5 “Graffiti”序列的性能比较 |
从带宽需求方面分析,当传输环境为TD-SCDMA理论峰值速率2.8 Mbps时,传输QCIF标准无损原数据的帧率为15帧/s,达到农村信息化建设中准实时视频监控需求。同样传输环境下,每分钟可连续传输D1标准无损原数据54张,而连续传输传统的D1标准视频图像仅有18张。可见,按照研究方法并行优化后,网络数据量明显减小,可有效降低带宽需求。
3 结论提出一种多媒体数据的并行管理框架。该框架改进了多媒体数据管理中典型的顺序执行方式,实现了标准数据生成和原始数据分析的并行处理。以图像分析为例,介绍了利用该并行管理框架进行优化设计的实现方式。实验证明,提出的多媒体数据的并行管理框架有助于减小多媒体数据在传输和处理过程中的数据量,易于多核处理器的优化,在一定程度上缓解了农村信息化建设中多媒体应用对TD-SCDMA网络传输带宽的需求。并且,为TD-SCDMA向TD-LTE过渡过程中多媒体数据的管理技术发展提供了新的启示。
| [1] |
李曼.
基于社会资本理论的农村信息化发展研究[J]. 科技进步与对策, 2009, 26(18): 56–59.
LI Man. The study on the informatization of the rural areas based on the theory of social capital[J]. Science & Technology Progress and Policy, 2009, 26(18): 56–59. (in Chinese) |
| [2] |
石宏, 杨骅.
我国TD-SCDMA产业的发展[J]. 电信快报, 2004, 9: 4–8.
SHI Hong, YANG Hua. The development of TD-SCDMA industry in China[J]. Telecommunications Information, 2004, 9: 4–8. (in Chinese) |
| [3] |
李德明.
多措并举——构建和谐行业生态[J]. 中国电信业, 2011(2): 44–47.
LI Deming. Take measures to build the harmonious industry environment[J]. China Telecommunications Trade, 2011(2): 44–47. (in Chinese) |
| [4] |
胡兴军.
我国TD-SCDMA产业化进展综述[J]. 有线电视技术, 2008, 15(2): 81–84.
HU Xingjun. The review of commercialization of TD-SCDMA in China[J]. CATV Technology, 2008, 15(2): 81–84. (in Chinese) |
| [5] |
张凯, 来志京, 田云飞.
TD-SCDMA到TD-LTE跨系统小区重选仿真研究[J]. 现代电信科技, 2010(12): 56–61.
ZHANG Kai, LAI Zhijing, TIAN Yunfei. The simulation of the re-selection from TD-SCDMA to TD-LTE[J]. Modern Science & Technology of Telecommunications, 2010(12): 56–61. DOI:10.3969/j.issn.1002-5316.2010.12.018 (in Chinese) |
| [6] |
曹折波, 李青.
多核处理器并行编程模型的研究与设计[J]. 计算机工程与设计, 2010, 31(13): 2999–3002.
CAO Zhebo, LI Qing. Research and design of parallel programming model on multi-core[J]. Computer Engineering and Design, 2010, 31(13): 2999–3002. (in Chinese) |
| [7] | Hytti H T. Characterization of digital image noise properties based on RAW data[J]. IS & T/SPIE Electronic Imaging:Image Quality and System Performance Ⅲ, 2006, 6059: 128–133. |
| [8] | Menon D, Calvagno G. Color image demosaicking:an overview[J]. Signal Processing:Image Communication, 2011, 26: 518–533. DOI:10.1016/j.image.2011.04.003 |
| [9] | Vandewalle P, Kpichane K, Alleysson D, et al. Joint demosaicing and super-resolution imaging from a set of unregistered aliased images[C]//Proceedings of IS & T/SPIE Electronic Imaging:Digital Photography Ⅲ, January 28-February 1, 2007, Jose, CA, USA.[S.l.]IS & T/SPIE Electronic Imaging:Digital Photography Ⅲ, 2007, 6502:1-20. |
| [10] | Ramanath R, Snyder W E, Bilbro G L. Demosaicking methods for Bayer color arrays[J]. Journal of Electronic Imaging, 2002, 11(3): 306–315. DOI:10.1117/1.1484495 |
| [11] | Li Z H, Gong W G, Nee A Y C, et al. Region-restricted rapid keypoint registration[J]. Optics Express, 2009, 17(24): 22096–22101. DOI:10.1364/OE.17.022096 |
| [12] | Liu T, Moore A, Gray A, et al. An investigation of practical approximate nearest neighbor algorithms[J]. Advances in Neural Information Processing Systems, 2004: 825–832. |
| [13] | Bovic A. Handbook of image and video processing (2nd ed)[M]. San Diego: Elsevier Academic Pres, 2005. |
| [14] | Lowe D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91–110. DOI:10.1023/B:VISI.0000029664.99615.94 |
| [15] | Martin A, Bolles R C. Random sample consensus:a paradigm for model fitting with applications to image analysis and automated cartography[J]. Communications of the ACM, 1981, 24(6): 381–395. DOI:10.1145/358669.358692 |
| [16] | Mikolajczyk K, Schmid C. A performance evaluation of local descriptors[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(10): 1615–1630. DOI:10.1109/TPAMI.2005.188 |
| [17] |
李正浩, 龚卫国, 倪亦靖, 等.
基于匹配技术的影像真实性鉴别[J]. 仪器仪表学报, 2009, 30(4): 876–881.
LI Zhenghao, GONG Weiguo, NI Yijing, et al. Image authenticity verification based on matching technology[J]. Chinese Journal of Scientific Instrument, 2009, 30(4): 876–881. (in Chinese) |
| [18] | 牛津大学仿射协变特征图像测试库[DB/OL]. http://www.robots.ox.ac.uk/~vgg/research/affine/, 2007. |
 2013, Vol. 36
2013, Vol. 36


