由于生命系统的高度复杂性以及研究的困难程度,心血管系统是较早地应用建模和仿真的领域之一。心血管系统建模仿真以血流动力学为基础,结合人体的解剖结构,建立相应的数学模型,可以揭示心血管系统的生理病理机理,为临床诊断和治疗提供理论依据和新思路[1-3]。因此当一个心血管系统的模型建立起以后,如能令其中的某些参数如血压、血流、外周阻力等作种种变化,就相当于制造了种种病例,从而预测某种生理病理疾病的发展趋势,并提出相应的防治措施。
心血管系统的数学模型多种多样,如系统辨识法[4]、有限元分析法[5]、功率键合图法[6]和电网络模型[7]。系统辨识法是利用控制理论中的系统辨识技术来对血液循环系统建模,它仅仅只强调了外部观测和系统在某方面的整体功能,模型参数的生理意义不明确,且模型的正确与否强烈依赖于输入输出提取的准确性,局限性较大。有限元分析法要求对系统的有关生理、解剖及物理参数有详尽的了解,同时用有限元分布参数模型模拟整个循环系统的计算量相当巨大,不便于应用。功率键合图建模法其建立过程比较繁琐,需要区分功率键、结点以及它们所代表的不同器官,容易出错。而电网络模型可克服上述缺点及不足,具有直观形象,容易实现,方便调节参数,可直接从电路图中得出想要的仿真结果等优点。对于上肢模型的研究,国内外学者中对其研究较少,白净等人先建立了一系列心血管系统的动力学分布式模型,为了研究桡动脉脉搏波,在原有模型上加上上肢部分,从力学的角度以寸、关、尺三个部分来观察脉搏波的变化。Noordergraaf及Westerhof等提出了反映人体55段主动脉的人体动脉树模型,把人体动脉树模型看作分布式的输电线网络。因此本文根据弹性腔理论,从电路学的角度建立上肢血管系统的集总参数电网络模型,利用Matlab中的Simulink和Simpowersystems模块对模型进行仿真研究,并将仿真结果与临床实测作对比分析。鉴于高血压和动脉硬化等疾病都会导致心血管系统动力性参数的变化,如高血压将会引起的外周阻力的增大和动脉硬化导致顺应性的减小,本文就外周阻力和顺应性的改变所致桡动脉脉搏波的变化进行了仿真研究。
1 原理 1.1 弹性腔理论与电网络模型早在19世纪末和20世纪初期,Frank建立起相当于动脉系统集中参数模型的风箱理论(Windkessel theory),亦称弹性腔理论[8-10]。把大动脉比拟为一个弹性腔,将小动脉和毛细血管比拟为弹性腔的外周阻力。心脏把血液压入弹性腔,然后血液再从弹性腔通过外周阻力流入到人体各部分组织,引入了单弹性腔模型。
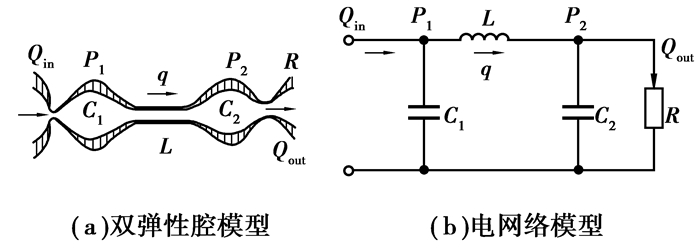
由于单弹性腔模型过于简化,1967年由美国的戈特温和瓦特共同提出了双弹性腔模型,双弹性腔模型将人体主动脉及其主要分支看作两个弹性腔。第一个弹性腔表征主动脉弓及其主要分支的集总顺应性(Compliance)C1;第二个弹性腔表征腹主动脉及其主要分支的集总顺应性C2;连接两腔体的血柱L表征血液的惯性。心脏收缩时,血液Qin由心室进入第一个弹性腔C1与血柱L,而后进入第二个弹性腔C2,最后流经集中的外周阻力R而进入静脉腔,如图 1所示。
|
图 1 动脉系统双弹性腔模型及其电网络模型 |
根据心血管动力学原理和流体网络理论,通过线性化假设导出的流体传输和等效网路与电气网络中相应的传输方程和等效电路有相同的数学形式[11-12],可以建立流体网络与电气网络各个参数之间的类比关系如下表 1所示。
| 表 1 生理参数与工程学参数的转换流体参数 |
从而可用电气网络理论的原理和方法去解决心血管网络中的传输和瞬变问题。图 1(b)就是根据流体网络和电气网络之间的等效关系得出动脉系统双弹性腔的电网络模型。
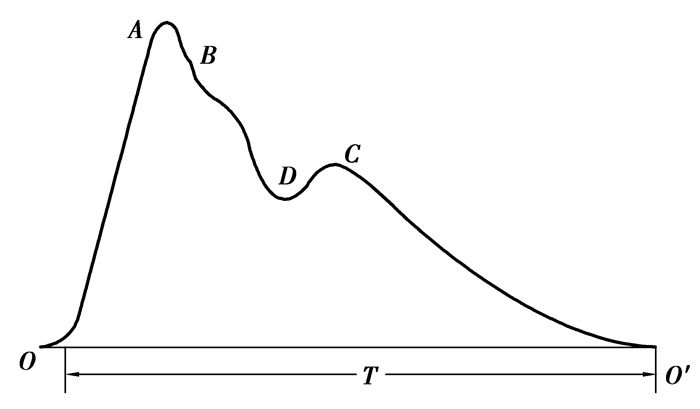
1.2 脉搏波与生理病理变化关系脉搏波形中包括1个升支和1个降支,如下图 2所示,升支代表心室收缩时动脉的突然扩张;降支表示心室舒张。升支一般迅速而平滑,它代表心室快速射血,主动脉血量增加及血压升高,其上升的速度及波幅的大小受射血速度、动脉阻力和动脉壁弹性的影响[13-14]。降支代表心室射血的后期,进入主动脉的血量少于由主动脉流向外周的血量,动脉血压逐渐降低。下降支部分的潮波,它是在减慢射血期后期心室停止射血,动脉扩张,血压下降,动脉内逆向流动而形成的反射波,主要与外周阻力、血管弹性及降支下降速度等变化有关。
|
图 2 脉搏波波形特征 |
脉搏波的幅值和波形变化反映出一个心动周期中动脉血压随时间的脉动变化。脉搏波中所包含的高血压和动脉硬化等信息主要反映在脉搏波的幅值和波形变化之中,如果进行波形特征分析,该信息又可以更加具体地将血压、血流、血管阻力和血管壁弹性等血流参数的变化表示出来。如外周阻力高时,脉搏波下降支的下降速率较慢,切迹的位置较高。外周阻力低时,下降支的下降速率较快,切迹位置较低,切迹以后下降支的坡度小,较为平坦[15]。而主波的高度主要反映左心室的射血功能和大动脉的顺应性。当动脉的顺应性C减小时,动脉弹性功能减弱,动脉血压的波动幅度增大,脉搏波上升支的斜率和幅度也加大[4]。
2 上肢的电网络模型由于动脉系统是全身分布动态系统,而要建立全身动脉系统的数学模型较难,从局部开始,以上肢为例建立人体血管系统的数学模型。根据弹性腔理论,假设动脉系统的模型是线性的和非时变的系统,动脉壁看作是不可压缩的,也就是说动脉壁被压缩时不会改变动脉的特征参数。在建立模型时只考虑主动脉和大动脉的影响,忽略其它的静脉和小动脉的影响。
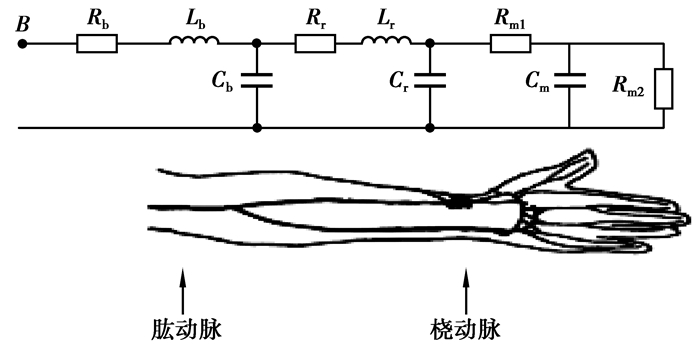
用三段式来表示上肢的模型,第一部分是肱动脉部分,即至肘关节处;第二部分是整个的桡动脉;第三部分是手的动脉参数。具体的电路模型如图 3所示。
|
图 3 上肢的电网络模型 |
其中Rb、Rr分别是肱、桡动脉的血流阻力;Lb、Lr分别是肱、桡动脉的血流惯性;Cb、Cr分别是肱、桡动脉的顺应性。Rm1、Rm2、Cm表示手掌的末端参数。把这三段模型应用到拉普拉斯域表示,从HA端看上去得到的阻抗为
| $ {{Z}_{\rm{H}}}\left( s \right)=\frac{s{{R}_{\rm{m1}}}{{R}_{\rm{m}2}}+{{R}_{\rm{m1}}}+{{R}_{\rm{m2}}}}{s{{R}_{\rm{m2}}}{{C}_{\rm{m}}}+1}。$ | (1) |
从RA端看上去得到的阻抗为
| $ \begin{array}{l} {Z_{{\rm{RA}}}}\left( s \right) = {R_r} + s{L_r} + \\ \frac{{s{R_{{\rm{m1}}}}{R_{{\rm{m2}}}}{C_{\rm{m}}} + {R_{{\rm{m1}}}} + {R_{{\rm{m}}2}}}}{{{s^2}{C_{\rm{r}}}{R_{{\rm{m}}1}}{R_{{\rm{m2}}}}{C_{\rm{m}}} + s({C_{\rm{r}}}{R_{{\rm{m}}1}} + {C_{\rm{r}}}{R_{{\rm{m}}2}} + {R_{\rm{m}}}_2{C_{\rm{m}}}) + 1}}。\end{array} $ | (2) |
从BA端看上去得到的阻抗为
| $ \begin{array}{l} {Z_{{\rm{BA}}}}\left( s \right) = {R_{\rm{b}}} + s{L_{\rm{b}}} + \\ \frac{{Rr + sLr + \frac{{s{R_{{\rm{m}}1}}{R_{{\rm{m}}2}}{C_{\rm{m}}} + {R_{{\rm{m}}1}} + {R_{{\rm{m}}2}}}}{{{s^2}{C_{\rm{r}}}{R_{{\rm{m1}}}}{R_{{\rm{m2}}}}{C_{\rm{m}}} + s({C_{\rm{r}}}{R_{{\rm{m}}1}} + {C_{\rm{r}}}{R_{{\rm{m}}2}} + {R_{{\rm{m}}2}}{C_{\rm{m}}}) + 1}}}}{{s{C_{\rm{b}}}({R_{\rm{r}}} + s{L_{\rm{r}}} + \frac{{s{R_{{\rm{m1}}}}{R_{{\rm{m2}}}}{C_{\rm{m}}} + {R_{{\rm{m}}1}} + {R_{{\rm{m}}2}}}}{{{s^2}{C_{\rm{r}}}{R_{{\rm{m}}1}}{R_{{\rm{m}}2}}{C_{\rm{m}}} + s({C_{\rm{r}}}{R_{{\rm{m1}}}} + {C_{\rm{r}}}{R_{{\rm{m}}2}} + {R_{{\rm{m}}2}}{C_{\rm{m}}}) + 1}} + \frac{1}{{s{C_{\rm{b}}}}}}}。\end{array} $ | (3) |
其中:
| $ {R_{\rm{b}}} = \frac{{8\eta {l_{\rm{b}}}}}{{\pi {r_{\rm{b}}}^4}}, {R_{\rm{r}}} = \frac{{8\eta {l_{\rm{r}}}}}{{\pi {r_{\rm{r}}}^4}}{\rm{, }}({\rm{mmHg\cdot s/mL}})。$ | (4) |
| $ {\rm{ }}{L_{\rm{b}}} = {c_{\rm{u}}}\frac{{\rho {l_{\rm{b}}}}}{{\pi {r_{\rm{b}}}^2}}, {L_{\rm{r}}} = {c_{\rm{u}}}\frac{{\rho {l_{\rm{r}}}}}{{\pi {r_{\rm{r}}}^2}}, ({\rm{mmHg\cdot}}{{\rm{s}}^2}/{\rm{mL}})。$ | (5) |
| $ {C_{\rm{b}}} = \frac{{\pi {r_{\rm{b}}}\mathit{\Delta }{D_{\rm{b}}}{l_{\rm{b}}}}}{{PP}}, {\rm{ }}{C_{\rm{r}}} = \frac{{\pi {r_{\rm{r}}}\mathit{\Delta }{D_{\rm{r}}}{l_{\rm{r}}}}}{{PP}}, ({\rm{mL/mmHg}})。$ | (6) |
η是血液粘度(3.5×10-3mm·Hg·s),ρ是血液密度(1.056 g/cm3)。rb、rr分别是肱、桡动脉血管半径,可通过超声仪器测出;ΔDb、ΔDr是肱、桡动脉半径的改变量。cu是常数1.33,它表明在桡动脉处的血流呈抛物线分布;lb、lr分别表示部分肱动脉长度、整个桡动脉的长度,由于取的肱动脉部分只是一部分,而桡动脉是整个部分,本文近似取lb/lr=1:20;PP是脉压(收缩压与舒张压的差值),可通过动脉硬化检测装置测量。
3 基于Simulink/Simpowersystem的上肢的仿真模型 3.1 信号源的提取在进行人体上肢的电网络模型仿真时,由于脉搏波是不规则的周期波形,怎样将采集到的脉搏波作为模型的输入信号是仿真需要解决的首要问题。
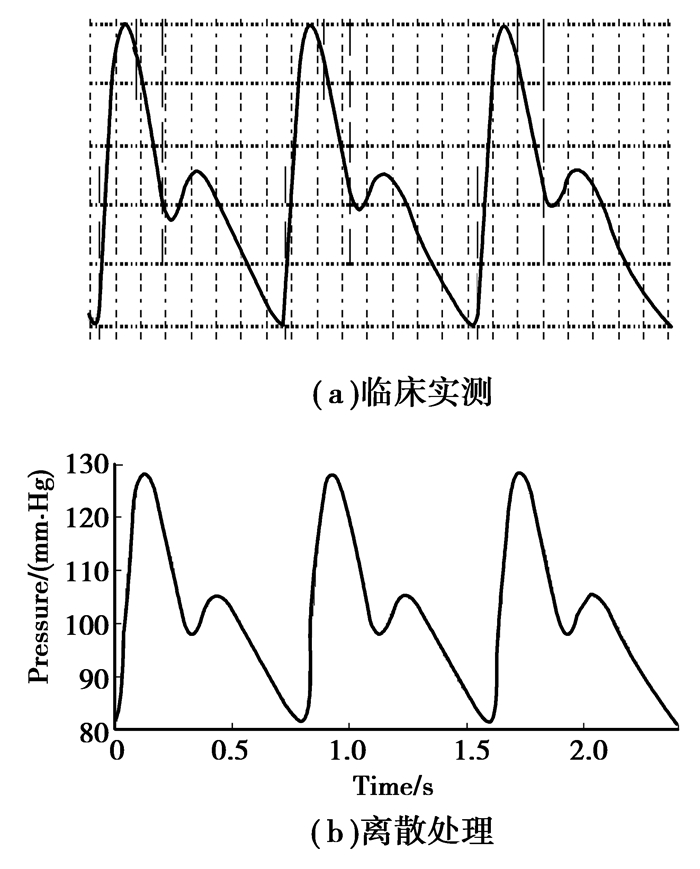
从日本欧姆龙的动脉硬化检测装置BP-203RPEII测出一健康人左上臂的脉搏波波形如下图 4(a)所示:以左上臂的波形作激励源。由于脉搏波是不规则的周期波形,所以将上述测量的图形先离散化处理后,再经傅里叶变换,借助MATLAB工具编程将其转化成规则图形的叠加。
|
图 4 肱动脉压力波形 |
将经离散化和傅里叶变换处理的激励源导入到MATLAB的工作空间中,通过直接调用工作空间里的数据进行建模和仿真。经处理后的信号源如图 4(b)所示,利用Matlab中的Simulink模块和Simpowersystems模块对上肢进行建模仿真时,由于Simpowersystems模块与常规的Simulink模块毕竟是两类本质不同的模块。所以,对于同时使用两类模块的仿真模型,必然会有两类模块之间的信号流动,这就需要中间接口模块。采用可控电压源作为中间接口模块,将Simulink模块的信号送入Simpowersystems模块,而采用电流和电压测量模块将Simpowersystems模块中的信号反馈给Simulink模块。
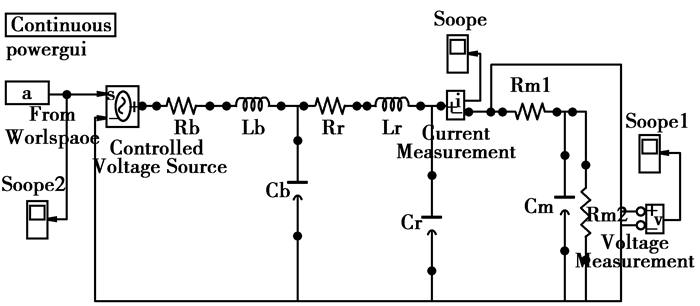
3.2 电网络模型框图人体上肢的电网络模型仿真框图如图 5所示,图中示波器2(Scope2)显示输入波形,通过From Workspace模块从工作空间中导入信号用作激励源,是经动脉硬化检测装置测量的左上臂的波形经离散化处理后的波形,如下图 6所示。Controlled Voltage Source作为Simulink模块和Simpowersystems模块之间的接口模块,将Simulink模块的信号送入Simpowersystems模块。而图中电路的元器件和图 3中上肢的电网络模型相对应的。Voltage Measurement和Current Measurement将Simpowersystems模块中的信号反馈给Simulink模块的。Current Measurement测得的是桡动脉处的血流情况,而Voltage Measurement测得的是桡动脉压力脉搏波。
|
图 5 上肢的仿真框图 |
|
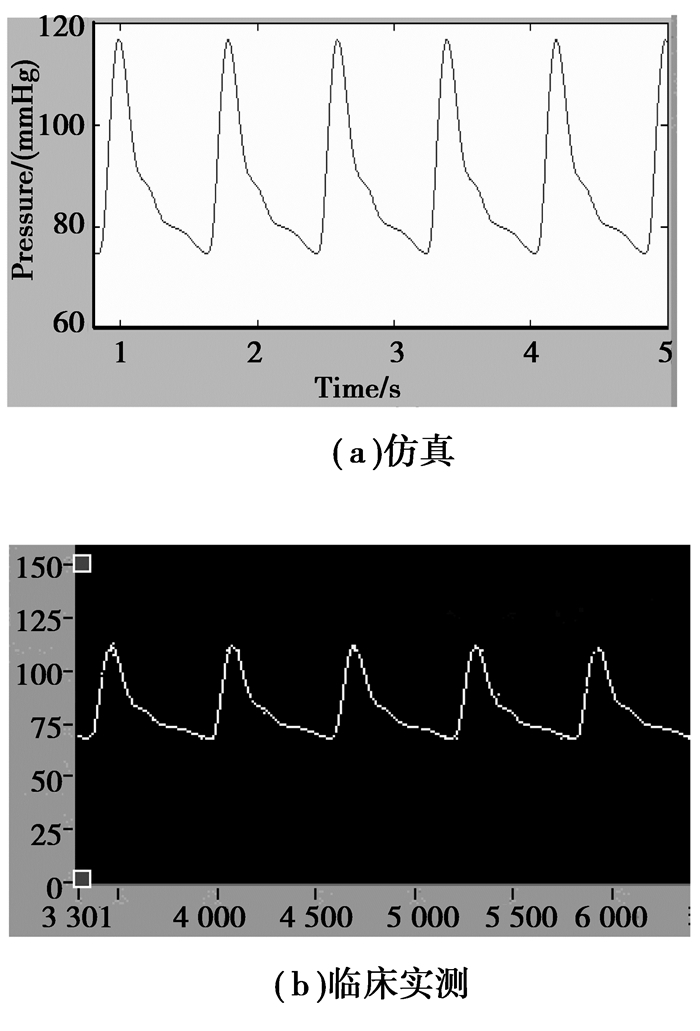
图 6 桡动脉压力波形 |
建立的Simulink/SimPowerSystems电网络模型采用变步长的ode45仿真算法,仿真的相对误差限取10-3,仿真时间设置为5s,按健康人的标准设定参数,如将人体心率设置为75 beat/min(即心动周期为0.8 s),仿真结果通过示波器显示。
同时,研究中采用动脉硬化检测仪YF/XGYD进行对比分析和研究。该动脉硬化检测仪系我们和四川宇峰科技有限公司合作研制,(采样频率为600 Hz)通过该仪器测出桡动脉脉搏波如图 6所示。
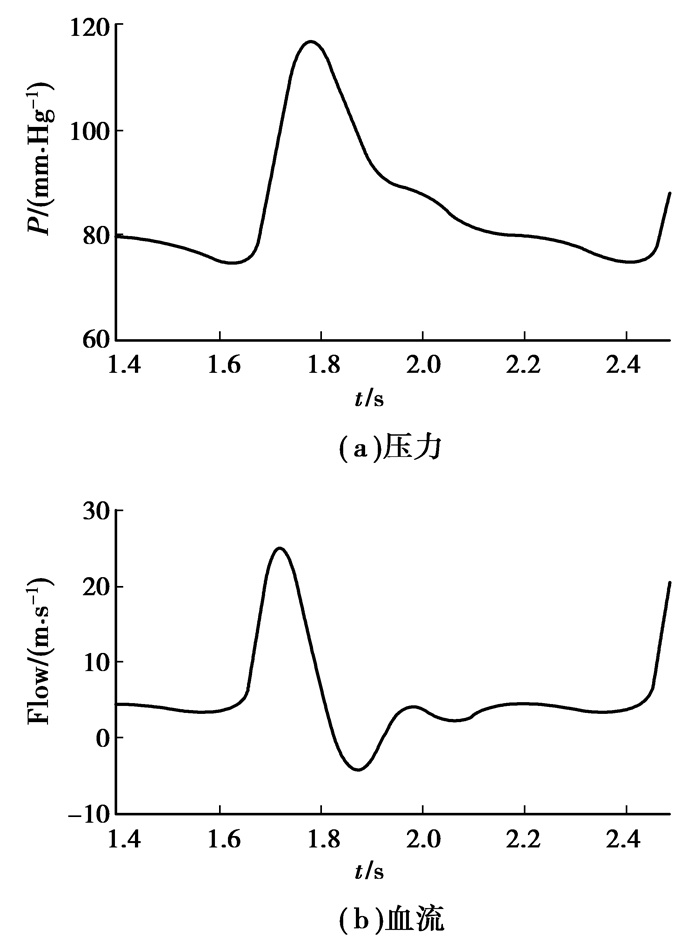
仿真的桡动脉的压力、血流波形如图 7所示。由图 6可知仿真结果与临床测试结果基本相符,证明了模型的有效性。
|
图 7 桡动脉压力和血流波形 |
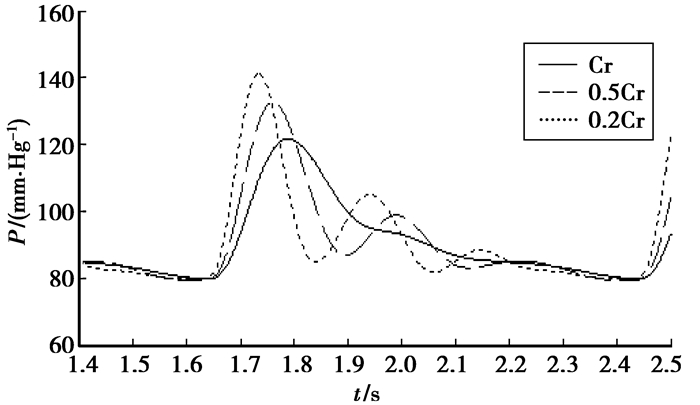
血管的顺应性C反应了血管的弹性功能,其值越小,动脉的弹性功能越差。通过建立的电网络模型分别就顺应性正常时及将顺应性减小到0.5倍及0.2倍时如图 8所示对模型进行仿真分析,对应图 5中桡动脉顺应性Cr的变化。从图中结果可知,桡动脉血管顺应性减小时,脉搏波上升支的斜率和幅度加大,重搏波变明显,脉压差增大。
|
图 8 血管顺应性变化时桡动脉压力波形 |
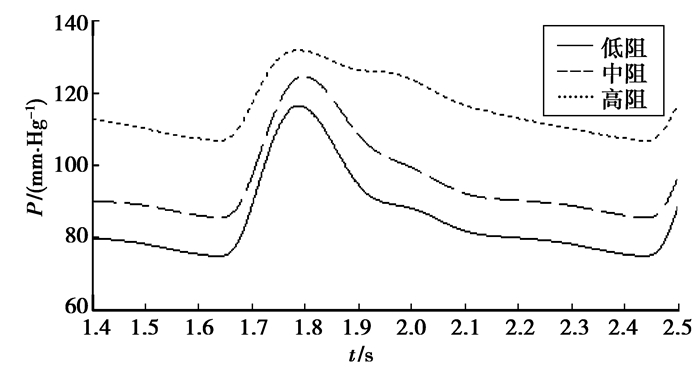
增大外周血流阻力是临床上高血压的常见症状,外周阻力增加,血压增高。通过建立的电网络仿真模型,分别就外周阻力为低阻(Rm1)、中阻(2Rm1)、高阻(5Rm1)时如图 9所示进行仿真分析。经比较可见,当外周阻力增大,脉搏波下降支的下降速率较慢,切迹的位置较高,脉搏波收缩期和舒张期压力均上升,但舒张期压力增大较收缩期大,故脉压差呈减小趋势。
|
图 9 外周阻力变化时桡动脉压力波形 |
动脉硬化检测仪(YF/XGYD)对142位受试者正常人组81人(男51,女30),高血压患者组61人(收缩压≥140,舒张压≥90 mmHg)(男36,女25)进行临床试验,测量其桡动脉顺应性和外周阻力,统计结果如下表 2所示。
| 表 2 正常人和高血压患者心血管动力学参数均值统计 |
由临床统计结果表 2可知,高血压组的桡动脉的顺应性和外周阻力与正常人比较都会发生相应的变化,桡动脉顺应性会减小约0.4倍而外周阻力会增大4倍左右,由此可看出高血压通常会导致外周阻力的增大和顺应性的减小。通过该电网络模型的仿真,当改变模型中外周阻力和桡动脉顺应性时,得出的结论中脉搏波的变化趋势与前面理论部分所述相符,从而验证了模型的有效性。
4 结论Windkessel模型出发,通过电气网络和流体力学之间的等比关系建立了一个人体上肢的电网络模型,通过仿真实验模拟出符合人体心血管系统生理情况的结果。鉴于生命系统的高度复杂性以及研究的困难程度,仿真过程中我们对模型和参数都做了适当的提炼。后续研究中,将进一步完善上肢的模型,逐步建立下肢、心脏及其全身的电网络模型,并将模型和临床实验作对照,可确定人体血管的阻塞情况。这些研究结果可以预测人体心血管系统的生理病理状态,对我国心血管病方面流行病学的调查、疾病预防和疾病的早期发现及诊断都具有一定的应用价值。
| [1] |
胡喆, 刁颖敏.
心脏-肺循环-体循环系统建模初探[J]. 同济大学学报:自然科学版, 2002, 30(1): 61–65.
HU Zhe, DIAO Yingmin. Primary model of heart-systemic-pulmonary system[J]. Journal of Tongji University:Natural Science Edition, 2002, 30(1): 61–65. (in Chinese) |
| [2] | Sugawara M, Niki K, Ohte N, et al. Clinical usefulness of wave intensity analysis[J]. Medical & Biological Engineering & Computing, 2009, 47(2): 197–206. |
| [3] | Marchandise E, Willemet M, Lacroix V. A numerical hemodynamic tool for predictive vascular surgery[J]. Medical Engineering & Physics, 2009, 31(1): 131–144. |
| [4] | 罗志昌, 张松, 杨益民. 脉搏波的工程分析与临床应用[M]. 北京: 科学出版社, 2006. |
| [5] | Westerhof N, Lankhaar J W, Westerhof B E. The arterial Windkessel[J]. Med Biol Eng Comput, 2009, 47: 131–141. DOI:10.1007/s11517-008-0359-2 |
| [6] |
宁钢民, 代开勇, 李英奇, 等.
心血管系统键合图模型研究[J]. 浙江大学学报:工学版, 2007, 41(5): 864–870.
NING Gangmin, DAI Kaiyong, LI Yingqi, et al. Bond graph model for cardiovascular system[J]. Journal of Zhejiang University. Engineering Science, 2007, 41(5): 864–870. (in Chinese) |
| [7] | Alastruey J, Parker K H, Peiré J, et al. Modelling the circle of Willis to assess the effects of anatomical variations and occlusions on cerebral flows[J]. Journal of Biomechanics, 2007, 40(8): 1794–1805. DOI:10.1016/j.jbiomech.2006.07.008 |
| [8] | 柳兆荣, 李惜惜. 弹性腔理论及其在心血管系统分析中的应用[M]. 北京: 科学出版社, 1987. |
| [9] | Zhu Y, Spraque B J, Phernetton T M, et al. Transmission line models to simulate the impedance of the uterine vasculature during the ovarian cycle and pregnancy[J]. European Journal of Obstetrl & Cynecology and Reproductive Blology, 2009, 144(Sup1): 184–191. |
| [10] | McDonald D A. Blood flow in arteries[M]. Baltimore: Williams & Wilkins, 1960. |
| [11] |
陈义清, 何为.
用示波法计算动脉顺应性的研究与实现[J]. 重庆大学学报:自然科学版, 2005, 28(9): 35–38.
CHEN Yiqing, HE Wei. Research realization of calculating artery compliance using oscillmetric method[J]. Journal of Chongqing University:Natural Science Edition, 2005, 28(9): 35–38. (in Chinese) |
| [12] | Peng X Q, Recchia F A, Byene B J, et al. In vitro system to study realistic pulsatile flow and stretch signaling in cultured vascular cells[J]. American Journal of Physiology, Cell Physiology, 2007, 279(3): 797–805. |
| [13] | Qiu Y, Tarbell J M. Interaction between wall shear stress and circumferential strain affects endothelial cell biochemical production[J]. Journal of Vascular Research, 2008, 37(3): 147–157. |
| [14] | Liang F Y, Takagi S, Himeno R, et al. Biomechanical characterization of ventricular-arterial coupling during aging:a multi-scale model study[J]. Journal of Biomechanics, 2009, 42(6): 692–704. DOI:10.1016/j.jbiomech.2009.01.010 |
| [15] | Liang F Y, Takagi S, Himeno R, et al. Multi-scale modeling of the human cardiovascular system with applications to aortic valvular and arterial stenoses[J]. Medical & Biological Eng ineering & Computing, 2009, 47(7): 743–755. |
 2013, Vol. 36
2013, Vol. 36


