近年来,神经网络被广泛应用于旋转机械的故障诊断,取得了不错的效果,但传统的人工神经网络不能解决旋转机械故障分类边界的模糊性问题。而且应用问题的规模往往很大,理论上要求求解这个问题的网络规模和实例规模相匹配[1]。传统的人工神经网络,如BP神经网络、自组织特征映射人工神经网络(SOFM)等不能解决上述旋转机械故障诊断的两个问题,导致故障诊断分类不够准确,诊断正确率不高。提出的自学习模糊脉冲神经网络[2-4](SLFSNN),目前在国内外应用都较少,主要应用在统计人口种群分布和图像处理方面,尤其在图像分割方面取得了较好的应用效果[5-9]。SLFSNN为基于脉冲神经网络的模糊聚类分析,它采用更接近于生物神经元的动态的脉冲神经元作为计算单元来进行信息编码和处理,结合聚类的无监督性和样本的先验知识,通过脉冲神经网络的精确聚类分析和迭代搜寻最优解。将SLFSNN算法应用于旋转机械故障诊断,并与传统的SOFM及BP网络诊断方法相比较,实验结果表明,SLFSNN不仅迭代次数少,而且聚类分析精度也得到较大的提高,较好地解决了故障分类的边界性问题及神经网络规模问题,较大提高了故障诊断的准确率。
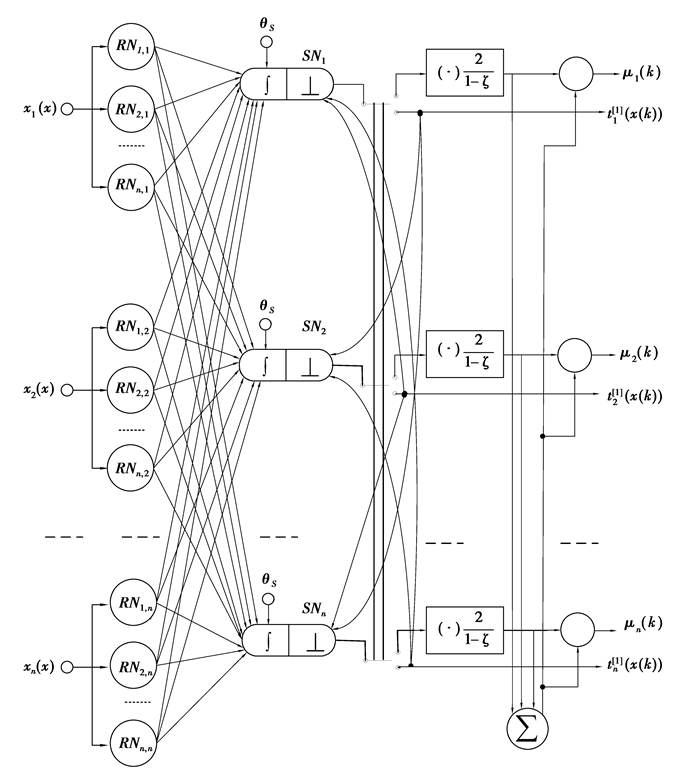
2 自学习模糊脉冲神经网络模糊脉冲神经网络SLFSNN是一个不均匀的3层前向反馈神经网络,其两个隐含层形成了自学习神经网络。在模糊脉冲神经网络中突触是变化的,突触分为两种,一种为输入层和隐层之间的兴奋性突触,另一种为隐藏层和输出层间的抑制性突触。下图是模糊脉冲神经网络的拓扑结构图。
|
图 1 SLFSNN的拓扑结构 |
输入神经元的功能是为了把特征数据编码成一个适当的频率范围,脉冲序列用线性编码方式生成这些特征数据。输入层总是有大量的预处理输入数据被要求典型地转化成暂态的脉冲序列数据,其中编码方式采用了频率数据点数并把它们转化成一个用于创建线性输入脉冲序列的间隔脉冲区间(ISI)。每个数据点被编码成一个特定的发放率,这个发放率被用于生成一个带恒定常数ISI的输入脉冲序列。
2.2 隐层2个隐含层中的第1个隐含层把(n×1)维输入模式x(k)(这里K是1个模式数)编码成脉冲t[0](x(k))的输入速度,其中每个脉冲称为它的点火周期。为提高聚类分析的精确性,在第1个隐含层里通过种群编码来增加输入维数。种群编码计划蕴含了1个输入xi(k)在同一时间被大量的感受野神经元RNli所处理,l=1, 2, ..h。作为一个规则,他们的激活功能是转换,折叠和钟形。
通常情况下一个感受野神经元发出的每个脉冲的点火周期落在一个特定的区间[0, tmax[0]]内,这个区间被称为编码间隔,可以表示成如下
| $ {t^{[0]}}(x(k)) = \left| {t_{\max }^{[0]}(1 - \psi (\left| {{x_i}(k) - c_{li}^{[0]}} \right|, {\sigma _i}))} \right|, $ |
其中|·|是层函数,ψ(·, ·)是感受野神经元的激励函数。
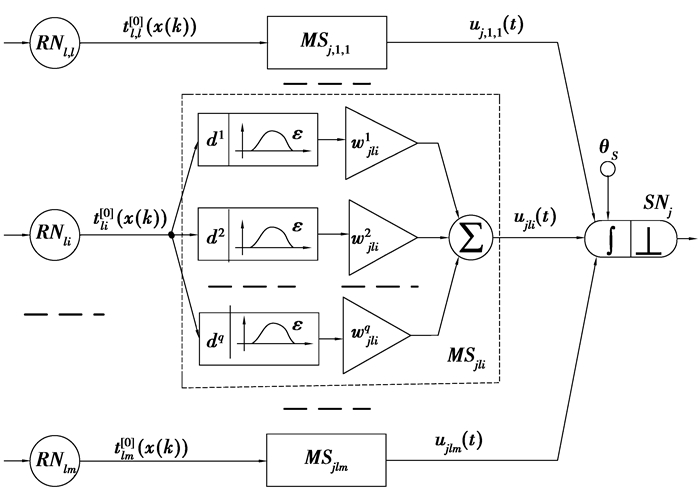
第2个隐含层由n个脉冲神经元SNj组成,j=1, 2…m。它们和前面的层通过多元突触相连接,如图 2所示。
|
图 2 多元突触结构 |
这个隐含层中1个多元突触是由一系列带有时间延迟d和变化的权重q的微突触组成。需要指出的是在多元突触内大量的微突触和一系列的时间延迟被整个神经网络所固定。第li个感受神经元有1个脉冲tli[0](x(k)), 第j个脉冲神经元得第p个微突触产生1个延迟了的突触后电位。
| $ {u_{jli}}^p\left( t \right) = {w_{jli}}^p{\varepsilon _{jli}}^p\left( t \right) = {w_{jli}}^p\varepsilon (t- ({t_{li}}^{[0]}\left( {x\left( k \right)} \right) + {d^p})), $ |
上式中ε(·)是一种脉冲响应函数,其表达式定义如下
| $ \varepsilon (t) = \frac{t}{\tau }\exp (1-\frac{t}{\tau })H(t)。$ |
式中τ是膜电位衰减时间常数,它的值能通过实证获得。
H(·)是Heaviide阶跃函数,多元突触MSjli的输出形成总的突触膜后电位
| $ {u_{jli}}(t) = \sum\limits_{p = 1}^q {u_{jli}^p(t)} 。$ |
每一个进来的突触膜后电位传递给脉冲神经元SN膜电位,如下表达式所示
| $ {u_j}(t) = \sum\limits_{i = 1}^n {\sum\limits_{l = 1}^h {{u_{jli}}(t)} } 。$ |
在一个模拟间隔中脉冲神经元SN在一个脉冲t的大部分时间里生成,在膜电位到达点火阈值θs的瞬间点火。学习阶段过后,每个脉冲神经元代表特定数据聚类中心,脉冲神经元的点火周期反映了输入模式到聚类中心的距离。第二个隐层的神经元通过横向抑制节点连接,使其它神经元在第一个神经元被点火之后点火,根据“胜者为王”规则定义输入模式的隶属度[10]。脉冲神经网络的学习算法是根据下面的规则更新突触权重得到的:那些对神经元的点火胜率有贡献的微突触的权重被加强,而那些没有贡献的微突触的权重被减弱。所以,这个规则使微突触权重wjli向输入模式xk附近获胜神经元的中心转移[11]。
2.3 输出模糊聚类层输出层,也被称为输出模糊聚类层,它提高了脉冲神经网络的性能,能在模糊领域里处理有效数据的聚类分析。训练的模糊脉冲神经网络能够成功解决各种变化的硬聚类数据分析任务。在模糊聚类模型中,脉冲神经网络包含三层,第二层的横向节点不起作用,模糊聚类层的输出在输入模式到每个脉冲神经元中心之间接收信息。输入模式到第j个聚类中心的隶属度是
| $ {\mu _j}(k) = \frac{{{{(t_j^{[1]}(x(k)))}^{\frac{1}{{1 - \xi }}}}}}{{\sum\limits_{\tau = 1}^m {{{(t_\tau ^{[1]}(x(k)))}^{\frac{1}{{1 -\xi }}}}} }}。$ |
其中ζ为模糊权系数,它决定最终划分的模糊量的集群和控制组之间的模糊边界。
2.4 SLFSNN诊断算法流程网络的算法流程如下:
1) 初始化:初始化权值矩阵w=[wij]m×ζ, i=1, 2, …, m, j=1, 2, …, ζ, ζ是模糊权系数,m是输入矢量的维数。设定迭代停止阈值ε。
2) 在m个学习模式中任选一个模式x(k)供给网络输入层,并计算矩阵范数
| $ {d_{\rm{g}}} = \left\| {{w_{jli}}(k)- {x_k}} \right\| = \sqrt {\sum\limits_{i = 1}^N {{{[w_{jli}^k(t)-x_i^k(t)]}^2}} }, $ |
计算出一个具有最小距离的脉冲神经元SNj。
3) 定义一个周围的邻域Ng(t), 使Ng(t)内的单元输出为1,Ng(t)外的单元输出为0。
4) 用Heeb规则修正脉冲神经元SNj及其邻域内的权值。权值调整公式如下
| $ \left\{ \begin{array}{l} {w_{jli}}^p\left( {K + 1} \right) = {w_{jli}}^p\left( K \right) + {\eta _w}\left( K \right)L(\mathit{\Delta }{t_{jli}}^p), j \in {N_g}\left( t \right);\\ {w_{jli}}^p\left( {K + 1} \right) = {w_{jli}}^p\left( K \right)j \notin {N_g}\left( t \right)。\end{array} \right. $ |
式中0 < ηw(k) < 1, ηw(k)为一学习因子,并随时间下降到0。
5) 将全部样本学习一遍作为一次循环,计算循环前后wjli的变化,当该变化小于阈值ε时,学习过程结束,否则转向步骤2)。
若把需诊断输入模式与网络输入层连接,按照上述学习算法进行迭代计算,模糊聚类层的获胜神经元就会兴奋起来,在输入模式到每个脉冲神经元之间接收信息,并依据隶属度公式识别输入信号的所属类别,实现对旋转机械故障的诊断[12-14]。
3 SLFSNN在旋转机械故障诊断中的应用 3.1 SLFSNN输入向量为检验SLFSNN算法的聚类有效性,以某热电厂汽轮机为例将SLFSNN诊断方法与SOFM算法进行比较。笔者收集了汽轮机组8种振动故障大量的现场试验数据建立故障样本,样本原始信号经过预处理,并去除噪声,选取其中40组典型数据建立故障样本集,样本维数为8,每维特征分别对应特征频谱0.01f~0.39f、0.40f~0.49f、0.50f、0.51f~0.99f、1.0f、2.0f、3~5f、>5f共8个频段的幅值,其中f为工频。表 1为40组样本中抽取的8组不同频段下的典型故障中心样本。
| 表 1 典型故障中心样本 |
表 2为2个诊断实例的待检故障样本。实例1,汽轮鼓风机组在运行过程中,2瓦、3瓦轴振动超标,对2瓦水平方向采集到的振动频谱进行特征提取并模糊预处理后,得到故障模式x1。实例2,汽轮机经过大修且过了大约一个月后,机组振动异常,相位极不稳定,振动值随转速升高明显加大,振动频谱的主要分量为基频,并带有明显的2f、3f及低频分量。
| 表 2 待检测故障样本待检故障样本 |
针对汽轮机组的实际工况,将上述40组典型故障样本分别输入SLFSNN和SOFM进行诊断测试仿真,并将SLFSNN与基于传统SOFM算法的诊断效果进行了比较,SLFSNN和SOFM的初始学习率均取0.2。硬件环境:CPU为Intel(R) core(TM)2, 主频为2 GHz, 内存为1 GHz。在Matlab7.0环境下两算法的训练耗时、诊断正确率及迭代次数的比较见表 3。
| 表 3 两种算法的实验结果 |
由表 3可知,SLFSNN比SOFM的迭代次数少,学习效率更高。将表 2的故障样本x1、x2分别送入已训练好的两种网络进行诊断比较,故障样本与哪种标准故障中心聚为一类,则说明该故障属于与模糊脉冲聚类中心同类的故障。诊断结果如表 4所示。
| 表 4 SLFSNN和SOFM诊断结果 |
上述少了比较,对实例1,两种算法诊断结果为:x1与F2聚为一类,表明该故障属于F2故障模式,即机组发生了不对中故障,与现场检查结果一致。对实例2,SLFSNN诊断结果:x2与F6聚为一类,其余各中心聚为一类,表明该故障模式属于F6的故障,即转子支承系统松动故障,与现场实际故障相符。SOFM诊断结果为x2既属于F2故障,又属于F6故障。实例2结果表明,SLFSNN比SOFM算法更有效,能较好地解决旋转机械故障分类边界的模糊性问题。
4 结论通过对SLFSNN和SOFM的诊断结果分析和比较,可以认为在旋转机械故障诊断中,基于自学习模糊脉冲神经网络算法比起传统的SOFM算法速度更快,诊断准确率更高,且它能通过自身的快速自学习能力和精确的聚类分析,有效地解决了应用问题规模和网络实例规模匹配的矛盾问题及故障分类边界的模糊性问题。
| [1] |
杨晓帆, 陈廷槐.
人工神经网络固有的优点和缺点[J]. 计算机科学, 1994, 21(2): 23–26.
YANG Xiaofan, CHEN Tinghuai. Inherent advantages and disadvantages of Artificial neural network[J]. Computer Science, 1994, 21(2): 23–26. (in Chinese) |
| [2] | Glackin C, Liam M, McDaid L, et al. Receptive field optimisation and supervision of a fuzzy spiking neural network[J]. Neural Networks, 2011, 24(3): 247–256. DOI:10.1016/j.neunet.2010.11.008 |
| [3] | Bodyanskiy Y, Dolotov A. Image processing using self-learning fuzzy spiking neural network in the presence of overlapping classes[C]//Proceedings of the 200811th International Biennial Baltic Electronics Conference (BEC2008), October 6-8, 2008, Tallinn, Estonia. Piscataway:IEEE Press, 2008:213-216. |
| [4] | Kubota N, Sasaki H. Genetic algorithm for a fuzzy spiking neural network of a mobile robot[C]//Proceedings of the 2005 IEEE International Symposium on Computational Intelligence in Robotics and Automation, June 27-30, 2005, Barcelona, Spain. Piscataway:IEEE Press, 2005:321-326. |
| [5] | Sheikhan M, Hemmati E. Trancsient chaotic neural network-based disjoint multipath routing for mobile ad-hoc networks[J]. Neural Computing and Applications, 2012, 21(6): 1403–1412. DOI:10.1007/s00521-011-0594-6 |
| [6] | Wade J J, McDaid L, Santos J A, et al. SWAT:an unsupervised SNN training algorithm for classification problems[C]//Proceedings of the 2008 International Joint Conference on Neural Networks, June 1-8, 2008, Hong Kong, China. Piscataway:IEEE Press, 2008:2648-2655 |
| [7] | Li A, Gu Q, Feng G C, et al. SNN:a neural network based combination of software reliability growth models[C]//Proceedings of the 20091st International Conference on Information Science and Engineering, December 26-28, 2009, Nanjing, China. Piscataway:IEEE Press, 2009:5109-5112. |
| [8] | Igwe P, Emrani M, Adeeb S, et al. Assessing torso deformity in scoliosis using self-organizing neural networks (SNN)[C]//Proceedings of the 2008 seventh International Conference on Machine Learning and Applications, December 11-13, 2008, San Diego, CA. Piscataway:IEEE Press, 2008:497-502. |
| [9] | Allen J N, Hasan S B, Abdel-Aty-Zohdy H S, et al. A low-power haar-wavelet preprocessing approach for a SNN olfactory system[C]//Proceedings of the IDT 20072nd International Design and Test Workshop, December 16-18, 2007, Cairo, Egypt. Piscataway:IEEE Press, 2007:222-225. |
| [10] | 高新波. 模糊聚类分析及其应用[M]. 西安: 西安电子科技大学出版社, 2004. |
| [11] | 马义德, 李廉, 王亚馥, 等. 脉冲耦合神经网络原理及其应用[M]. 北京: 科学出版社, 2006. |
| [12] |
谢志江, 程力旻, 陈平, 等.
模糊Kohonen神经网络回热系统故障诊断[J]. 重庆大学学报, 2008, 31(9): 992–996.
XIE Zhijiang, CHENG Limin, CHEN Ping, et al. Fuzzy fault diagnosis for a regenerative heating system based on a Kohonen neural network[J]. Journal of Chongqing University, 2008, 31(9): 992–996. DOI:10.11835/j.issn.1000-582X.2008.09.006 (in Chinese) |
| [13] |
李慧, 祁晓钰, 叶玉杰, 等.
SOFM神经网络在电动机故障诊断中的应用[J]. 装备制造技术, 2008(11): 23–24.
LI Hui, QI Xiaoyu, YE Yujie, et al. Application of self-organizing feature map neural network for fault diagnosis of motor[J]. Equipment Manufacturing Technology, 2008(11): 23–24. DOI:10.3969/j.issn.1672-545X.2008.11.009 (in Chinese) |
| [14] |
胡芳霞, 谢志江, 岳茂雄.
混沌粒子群优化模糊聚类的旋转机械故障诊断[J]. 重庆大学学报, 2011, 34(6): 26–30.
HU Fangxia, XIE Zhijiang, YUE Maoxiong. Fault diagnosis of rotating machinery based on fuzzy clustering optimized by chaos embedded particle swarm optimization[J]. Journal of Chongqing University, 2011, 34(6): 26–30. DOI:10.11835/j.issn.1000-582X.2011.06.005 (in Chinese) |
| [15] |
陈平, 谢志江, 欧阳奇.
多层传递函数的量子神经网络在汽轮机故障诊断中的应用[J]. 动力工程, 2007, 27(4): 569–572.
CHEN Ping, XIE Zhijiang, OU Yangqi. Application of quantum neural network based on multilevel transfer functions in fault diagnosis of steam turbine sets[J]. Power Engineering, 2007, 27(4): 569–572. (in Chinese) |
 2013, Vol. 36
2013, Vol. 36


