2. 重庆理工大学 计算机科学与工程学院 重庆 400050
2. College of Computer Science and Engineering, Chongqing University of Technology, Chongqing 400050, China
双足机器人具有与人相似的步行运动方式,对协助人类具有重要的意义,双足步行控制问题是双足机器人研究的前沿和热点之一,但由于其存在的高阶、强耦合和非线性等特性,实现快速稳定的动态步行仍然是一个挑战性的问题。
目前,双足机器人步行控制大多采用跟踪离线或在线生成的轨迹的控制方法,如基于ZMP(zero moment point)稳定判据的控制方法,使ZMP位于一定的支撑区域内[1-8],系统各个自由度直接可控。这种控制方法缩小了步行运动的范围, 当步行过程中出现脚部欠驱动相时[9],不再符合ZMP姿态稳定判据的要求。从控制理论的观点看,在稳定域附近的调整是小范围的,真正困难的是双足机器人在步行过程中经常处于不稳定域。
欠驱动双足机器人动态步行的研究给出了一种新的思路,这类机器人可控关节数小于自由度数,小腿末端与地面间处于点接触状态。Grizzle等通过对机器人施加一系列虚拟完整约束、计算Poincaré回归映射以实现欠驱动双足机器人动态行走[10-12]。但由于获得Poincaré映射理论方法的困难性和数值方法计算模型的复杂性,其应用仍具有很大的局限性。
人在步行过程中,特别是快速行走时,身体经常处于前倾状态,即通过不断打破所谓“稳定”来获得更高的速度。在完成这些动作的过程中, 身体各关节力的大小和方向的协调控制具有高度的技巧和动觉智能[13]。研究并模拟这些肢体运动技巧和动觉智能, 对建立双足机器人运动的智能控制理论和方法具有十分重要的意义。稳定快速步行是双足运动的基本动作之一,其中蕴涵了多个动觉智能基元,其运动控制研究对于模仿和认识人体的动觉智能的特征均有重要意义。
结合仿人智能控制具有多模态控制、简单易在实际系统实现的特点,在分析双足机器人动力学模型的基础上,应用基于动觉智能图式的仿人智能控制的分析设计方法, 设计了动态步行控制器, 并通过仿真实验验证了控制策略的有效性。
1 双足机器人模型假定双足机器人行走平面设定为矢状面xz平面内,机构包括躯干和完全相同的两腿,每条腿有两杆通过膝关节链接而成,膝和髋均为一自由度理想(无摩擦)旋转关节。机器人步行过程由单腿支撑阶段和双腿支撑阶段组成。
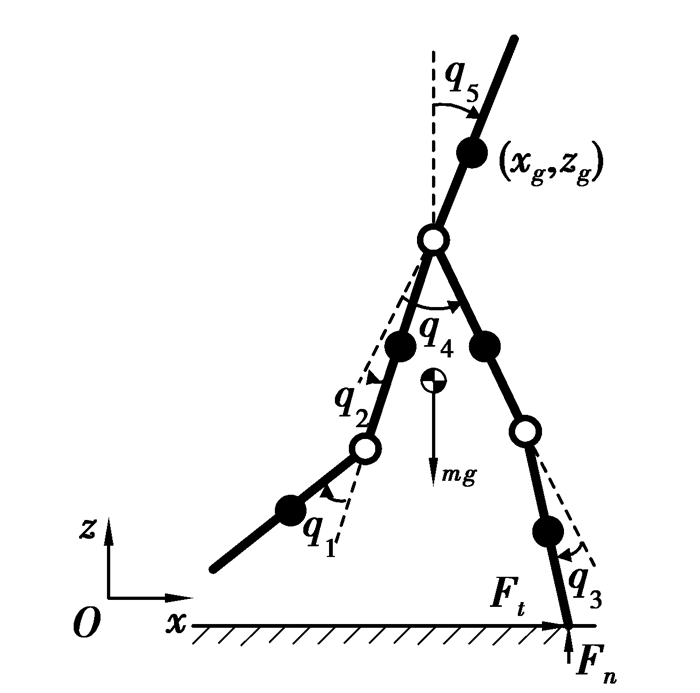
令qc=[q1, q2, q3, q4]T为机器人的位形相对坐标,q5为躯干与绝对坐标系z轴的夹角,pxz=(xg, zg)为躯干质心在绝对坐标系下的位置,qr=[q1, q2, q3, q4, q5, xg, zg]T为广义坐标,u=[u1, u2, u3, u4]T为机器人各杆链接处的关节驱动力矩,q=[q1, q2, q3, q4, q5]T为角度向量。如图 1所示。
|
图 1 双足机器人模型 |
双足机器人系统的拉格朗日方程形式为
| $ \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\frac{{\partial K}}{{\partial {{\dot q}_{{{\rm{r}}_n}}}}}} \right) - \frac{{\partial K}}{{\partial {q_{{{\rm{r}}_n}}}}} + \frac{{\partial P}}{{\partial {q_{{{\rm{r}}_n}}}}} = {Q_n},(n = 1,2, \cdots ,7), $ | (1) |
其中:K为系统的动能;P为系统的势能;Qn为广义力。
躯干质心和腿末端pek(xek, zek)位置关系可以表示为
| $ \left[{\begin{array}{*{20}{c}} {{x_g}}\\ {{z_g}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} {{x_{ek}}}\\ {{z_{ek}}} \end{array}} \right] + \left[{\begin{array}{*{20}{c}} {{f_{kx}}(q)}\\ {{f_{kz}}(q)} \end{array}} \right], $ | (2) |
其中:fk(q)=[fkx(q), fkz(q)]T, (k=1, 2)表示躯干质心和腿末端间关系的向量函数,由q和双足机器人物理参数共同决定,进而得到
| $ \mathit{\boldsymbol{K}} = \mathit{\boldsymbol{q}}_{\rm{r}}^{\rm{T}}\left[{\begin{array}{*{20}{c}} {\mathit{\boldsymbol{A}}({\mathit{\boldsymbol{q}}_c})}&0\\ 0&{M{\mathit{\boldsymbol{I}}_2}} \end{array}} \right]{\mathit{\boldsymbol{q}}_{\rm{r}}}, $ | (3) |
| $ \mathit{\boldsymbol{Q}} = \left[{\begin{array}{*{20}{c}} {{I_4}}\\ 0 \end{array}} \right]u + \sum\limits_{k = 1, 2} {\left[{\begin{array}{*{20}{c}} {-\frac{{\partial {\mathit{\boldsymbol{f}}_k}{{(\mathit{\boldsymbol{q}})}^{\rm{T}}}}}{{\partial \mathit{\boldsymbol{q}}}}}\\ {{\mathit{\boldsymbol{I}}_1}} \end{array}} \right]} {R_i}, $ | (4) |
其中:M为双足机器人的质量;A(qc)为5×5矩阵;
用分块矩阵表示式(1),机器人的动力学方程表示为
| $ \begin{array}{l} \left[{\begin{array}{*{20}{c}} \mathit{\boldsymbol{D}}&{\mathit{\boldsymbol{D}}_R^{\rm{T}}}\\ {{\mathit{\boldsymbol{D}}_R}}&{M{\mathit{\boldsymbol{I}}_2}} \end{array}} \right]{\mathit{\boldsymbol{q}}_r} + \left[{\begin{array}{*{20}{c}} \mathit{\boldsymbol{C}}&{{0_{5 \times 2}}}\\ {{\mathit{\boldsymbol{C}}_R}}&{{0_{2 \times 2}}} \end{array}} \right]{\mathit{\boldsymbol{q}}_r} + \left[{\begin{array}{*{20}{c}} G\\ {{G_R}} \end{array}} \right] = \\ \left[{\begin{array}{*{20}{c}} \mathit{\boldsymbol{B}}\\ {{0_{2 \times 4}}} \end{array}} \right]u + \mathit{\boldsymbol{J}}_1^{\rm{T}}{\mathit{\boldsymbol{R}}_1} + \mathit{\boldsymbol{J}}_2^{\rm{T}}{\mathit{\boldsymbol{R}}_2}, \end{array} $ | (5) |
其中,D(5×5)、DR(2×5)为惯性矩阵,C(5×5)、CR(2×5)为离心力和哥氏力矩阵,G、GR为重力项,B=[01×4; I4]表示关节驱动关系,J1、J2分别为腿末端作用力R1、R2对应的Jacobian矩阵。
2 基于动觉智能图式的步行控制应用基于动觉智能图式的仿人智能控制的分析设计方法,需要将目标动作划分为几个串行控制阶段,并为每个阶段分配不同的控制任务;各阶段内部又包含若干个并行或串行的控制模态,根据输入的特征模态来决定控制模态的执行[14-15]。
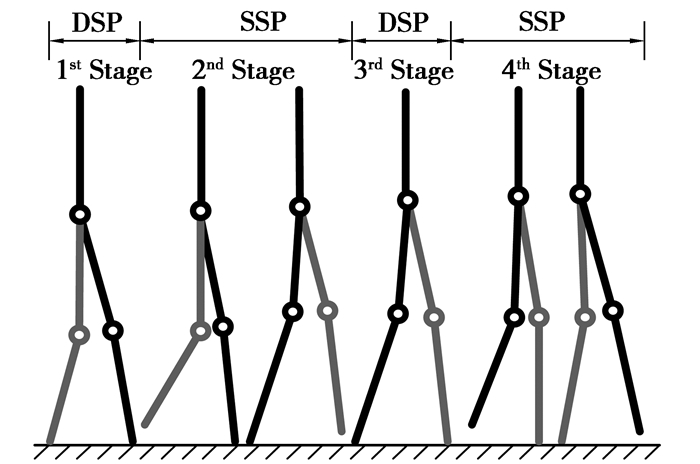
2.1 步行控制任务的分解通过对人类步行运动的观察,双足步行是支撑腿与摆动腿交替的周期性动作,基于动觉智能图式理论的仿人智能控制根据步行中摆动腿及支撑腿姿态的变化,将一个周期内的步行运动过程划分为4个串行的目标阶段:左腿在前双支撑相、左腿单支撑相、右腿在前双支撑相和右腿单支撑相。步行控制的关键为单支撑相摆动腿与支撑腿的协调运动,如图 2所示。DSP(double support phase)表示机器人处于双支撑相(左腿或右腿在前),SSP(single support phase)表示机器人处于单支撑相(左腿或右腿单支撑)。
|
图 2 双足步行任务分解 |
各目标阶段的双腿运动姿态具体描述如下:
1) 左腿在前双支撑相。
这个阶段的主要目标是调整左右腿髋、膝关节的初始角度和初始速度值,使双腿都处于适合进入下一阶段左腿单支撑相运动的状态。
2) 左腿单支撑相。
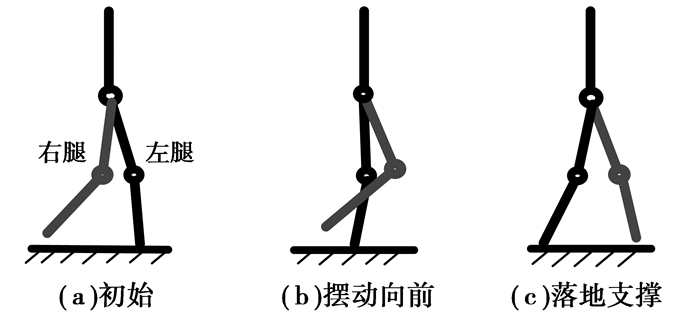
在左腿单支撑相,摆动腿动作变化最大,参照其不同运动姿态,可以将单支撑相划分为初始离地阶段、摆动向前阶段和落地支撑阶段,如图 3所示。
|
图 3 双足步行单步过程 |
ⅰ)初始离地阶段,右大腿向前摆起一定角度,右小腿后摆离地,左腿保持支撑动作,如图 3(a)所示;
ⅱ)摆动向前阶段,右大腿继续向前摆起,右小腿保持一定夹角摆过躯干中线,左腿保持支撑同时其大腿绕左髋关节顺时针转动,躯干质心前移,如图 3(b)所示;
(ⅲ)落地支撑阶段,右小腿绕膝关节逆时针转动伸展至一定角度开始落地,左腿保持支撑同时左大腿继续绕左髋关节顺时针转动,如图 3(c)所示。
3) 右腿在前双支撑相
这个阶段的控制目标是调整上一阶段中的双腿姿态,使得左右腿都处于适合进入下一阶段右腿单支撑相运动的状态。
4) 右腿单支撑相
在右腿单支撑相,左腿变为摆动腿,姿态运动过程也可以划分为初始离地阶段、摆动向前阶段和落地支撑阶段,左腿摆动及右腿支撑过程与左腿单支撑相类似。
2.2 步行控制的动觉智能图式群用SKGij(i=1, 2, 3, 4;j=1, 2, 3, 4)表示第i阶段4个驱动关节的输出,用表示运动趋势的各关节夹角误差ej和夹角的变化速度dej表征姿态,用Δe=e4-e2表征左右大腿与躯干间的夹角之差。依据对上述4个串行阶段目标动作的规划及其中单个阶段机器人的动力学特征,结合误差相平面分析法,可得到动觉智能图式群。
在一个步行周期内,双支撑相可根据初始目标值采用PD控制调整步行姿态;由于步行中摆动腿小腿在离地与落地阶段具有重要作用,因此步行控制的关键为单支撑相内摆动腿小腿与大腿及支撑腿的协调运动,这里主要对单支撑相进行说明。
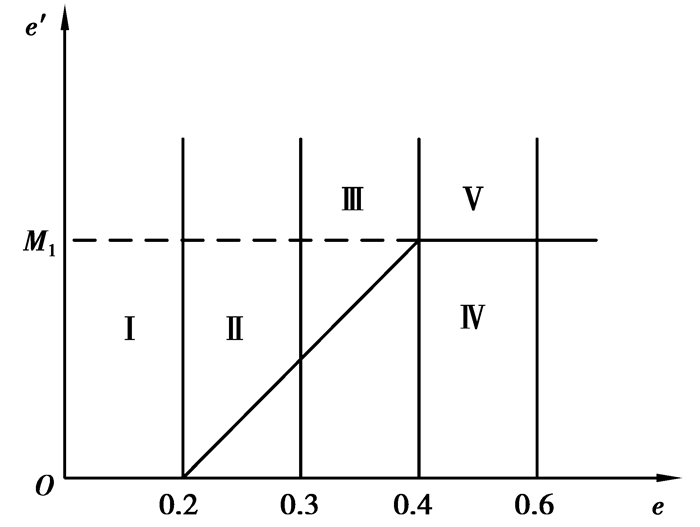
以第2阶段左腿单支撑相为例,右膝关节角误差相平面图如图 4所示,将0.4作为区分摆动腿膝关节角离目标远近的界限。当摆动腿膝关节角小于0.4时,采用正向大力矩,激发右小腿的速度,但此时还必须考虑右大腿的运动情况,当从左腿在前双支撑相转换到左腿单支撑相时,首先应使右大腿以较大的速度向前摆起,若右小腿顺时针转动过快会给右大腿一个反向作用,阻碍e2的变化,所以这阶段一开始(图 4区域Ⅰ和Ⅱ), 正向的u4值应较小,以让右大腿摆起。当e4≥0.3右小腿有了一定速度后(图 4区域Ⅲ),再将u4增大到关节力矩的最大值。e4>0.6后, 应控制右小腿的运动速度。图 4中区域Ⅳ使用比例控制激发速度,区域Ⅴ采用比例微分控制抑制速度。当从摆动向前阶段进入落地支撑阶段时,采用PD控制右小腿稳定落地。
|
图 4 第2阶段右膝关节角误差相平面图 |
可得到左腿单支撑相右腿膝关节的动觉智能图式
| $ \begin{array}{l} {S_{KG21}}:{u_1} = {k_{p21}}({e_1}-0.04) + {k_d}_{21}d{e_1}{\rm{; }}\\ {S_{KG22}}:{u_2} = {k_{p22}}({e_2} + 0.23) + {k_d}_{22}d{e_2}{\rm{;}}\\ {S_{KG23}}:{u_3} = {k_{p23}}({e_3}-0.1) + {k_d}_{23}d{e_3}. \end{array} $ |
| $ {S_{KG24}}:\left\{ \begin{array}{l} {u_4} = \left\{ \begin{array}{l} {k_{p24}}({e_4}-0.6), {\rm{d}}{e_4} < {\rm{ }}{M_1}; \cap (0.4{\rm{ }} < {\rm{ }}{e_4} < {\rm{ }}0.6) \cap \left( {\Delta {\rm{ }}e{\rm{ }} < {\rm{ }}0.2} \right);\\ {U_{H24}}, {e_4} < {\rm{ }}0.3 \cap \left( {\Delta {\rm{ }}e{\rm{ }} < {\rm{ }}0.2} \right);\\ U{'_{H24}}0.3{\rm{ }} < {\rm{ }}{e_4} < {\rm{ }}0.4 \cap \left( {\Delta {\rm{ }}e{\rm{ }} < {\rm{ }}0.2} \right){\rm{;}}\\ {k_{p24}}({e_4}-0.6) + {k_d}_{24}{\rm{d}}{e_4}{\rm{, d}}{e_4} > {\rm{ }}{M_1} \cap (0.4{\rm{ }} < {\rm{ }}{e_4} < {\rm{ }}0.6) \cap \\ \left( {\Delta {\rm{ }}e{\rm{ }} < {\rm{ }}0.2} \right); \end{array} \right.\\ {u_4} = {k_{p2}}({e_4}-0.2) + {k_d}_2{\rm{d}}{e_4}, \Delta {\rm{ }}e{\rm{ }} > {\rm{ }}0.2 \end{array} \right. $ | (6) |
对右腿单支撑相,输出控制可以看作是左右腿交换情形,同理可得
| $ \begin{array}{l} {S_{KG41}}:{u_1} = {k_{p41}}({e_1}-0.04) + {k_d}_{41}{\rm{d}}{e_1}, {\rm{ }}\\ {S_{KG42}}:{u_2} = {k_{p42}}({e_2} + 0.23) + {k_d}_{42}{\rm{d}}{e_2}, {\rm{ }} \end{array} $ |
| $ \begin{array}{l} {S_{KG43}}:\left\{ \begin{array}{l} {u_3} = \left\{ \begin{array}{l} {k_{p43}}({e_3}-0.6), {\rm{d}}{e_3} < {\rm{ }}{M_2} \cap (0.4{\rm{ }} < {\rm{ }}{e_3} < {\rm{ }}0.6) \cap \left( {\Delta {\rm{ }}e{\rm{ }} > {\rm{ }}-0.2} \right);{\rm{ }}\\ {U_{H43}}, {e_3} < {\rm{ }}0.3 \cap \left( {\Delta {\rm{ }}e{\rm{ }} > {\rm{ }}-0.2} \right);\\ U{'_{H43}}.0.3{\rm{ }} < {\rm{ }}{e_3} < {\rm{ }}0.4 \cap \left( {\Delta {\rm{ }}e{\rm{ }} > {\rm{ }} - 0.2} \right);\\ {k_{p43}}({e_3} - 0.6) + {k_d}_{43}{\rm{d}}{e_4}, {\rm{d}}{e_3} > {\rm{ }}{M_2} \cap (0.4{\rm{ }} < {\rm{ }}{e_3} < {\rm{ }}0.6) \cap \\ \left( {\Delta {\rm{ }}e{\rm{ }} > {\rm{ }} - 0.2} \right); \end{array} \right.\\ {u_3} = {k_{p4}}({e_3} - 0.2) + {k_{d4}}{\rm{d}}{e_4}, \Delta {\rm{ }}e{\rm{ }} < {\rm{ }} - 0.2; \end{array} \right.\\ {S_{KG44}}:{u_4} = {k_{p44}}({e_4} - 0.1) + {k_d}_{44}{\rm{d}}{e_3}. \end{array} $ | (7) |
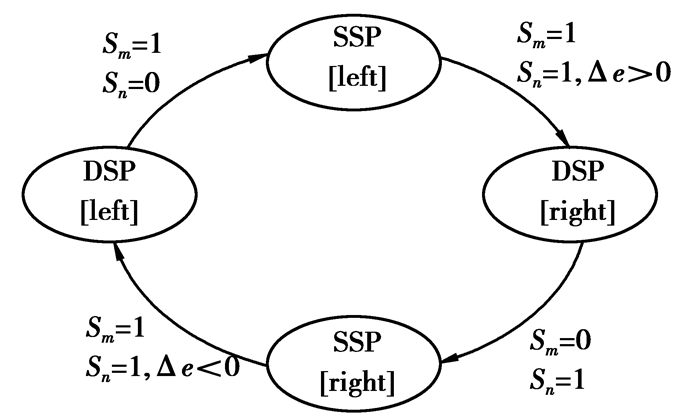
周期步行时序规划控制图式如图 5所示,Sm、Sn分别表示左右腿与地接触情形,Δe正负表示左右腿姿态前后关系。
|
图 5 周期步行规划图式 |
利用Matlab的仿真工具Simulink建立双足机器人步行仿真模型,地面接触力采用弹簧阻尼模型计算,假设双腿与地接触端各有一个弹簧阻尼模型,取弹性系数K=10 000 N/m,阻尼系数C=500 N·s/m。仿真采样时间为0.005 s。机器人结构参数如表 1所示。
| 表 1 双足机器人结构参数模型参数 |
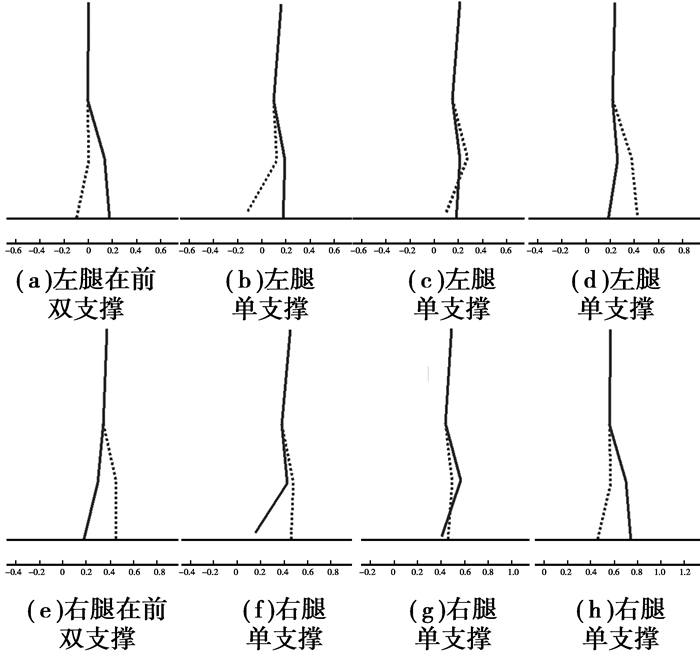
步行控制结果动画显示由人机界面GUI完成,一个步行周期内机器人动态步行各阶段结果如图 6所示。图 6(a)为左腿在前双支撑相结束时的姿态;图 6(b-d)为左腿单支撑相的姿态,依次表示初始离地、摆动向前和落地支撑阶段;图 6(e)为右腿在前双支撑相结束时的姿态;图 6(f-h)为右腿单支撑相的姿态。可见,用仿人智能控制方法设计的步行运动控制器,实现了姿态控制目标。
|
图 6 一个周期内的步行姿态 |
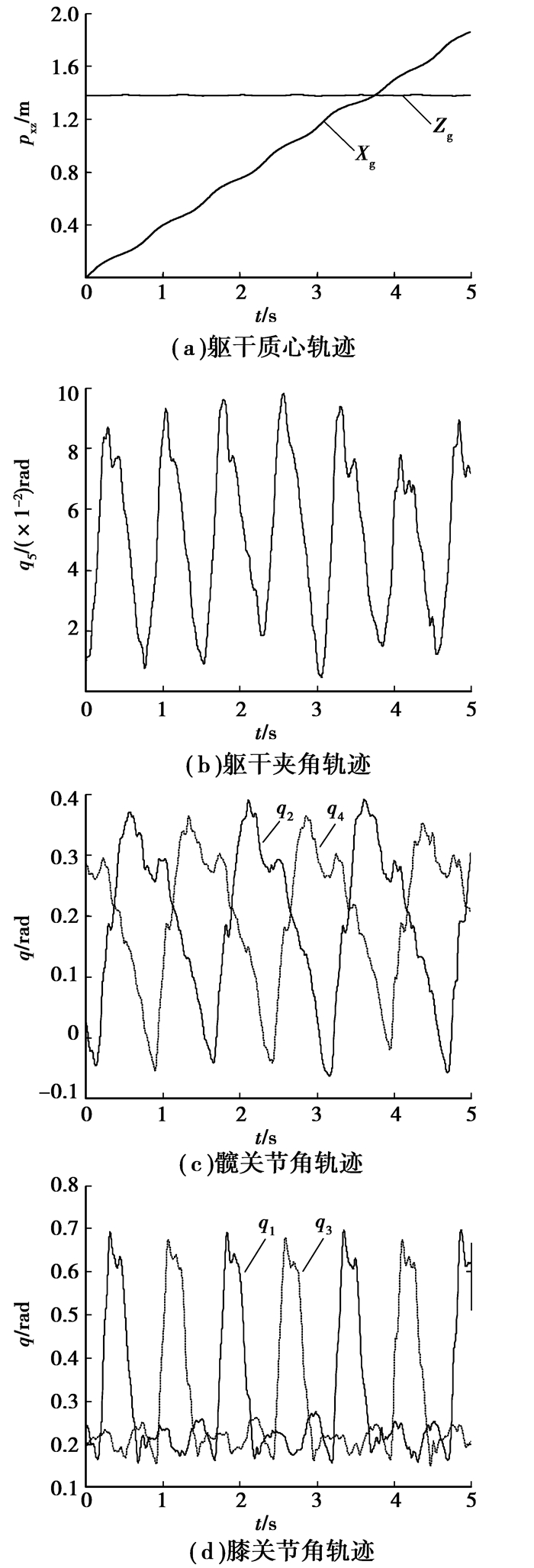
连续步行中双足机器人的躯干质心位置和各关节角变化如图 7所示。
|
图 7 连续步行躯干质心及关节角变化 |
矢状面内前向步行过程中,躯干质心纵坐标zg近似为一条直线、躯干夹角保持在较小的波动范围内,有利于机器人稳定连续步行,如图 7(a)、(b)所示;左右腿髋关节角和膝关节角周期性协调变化,表明双腿摆动或支撑动作呈周期性交替出现,如图 7(c)、(d)所示。
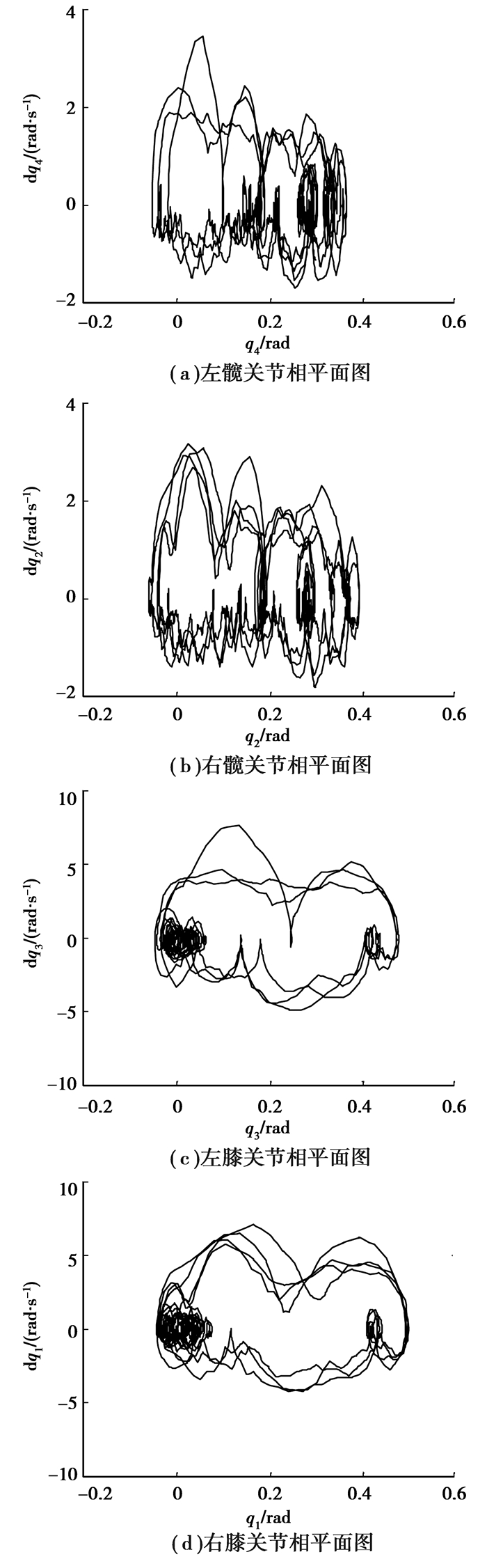
双足稳定步行状态最终会收敛于稳定的极限环[16]。双足机器人各关节行走相平面如图 8所示,实现连续稳定步行。
|
图 8 连续步行关节相平面图 |
应用基于动觉智能图式的仿人智能控制, 实现了双足机器人连续动态稳定步行的控制目标。
4 结论主要研究了双足机器人动态步行控制问题,在分析平面五杆双足机器人动力学模型的基础上, 将动态步行复杂控制任务分解为顺序执行的4个过程,应用基于动觉智能图式的仿人智能控制的分析设计方法, 结合相平面法定性定量的分析, 设计了适合双足机器人动态步行控制的动觉智能图式群。
仿真结果表明,该控制方法实现了双足机器人连续动态步行运动,控制方式简单,使双足步行控制不局限于基于ZMP的方法,对实现大步幅快速步行、动态跑步等具有一定的借鉴作用。
| [1] | Lim H, Ogura Y, Takanishi A. Locomotion pattern generation and mechanisms of a new biped walking machine[J]. Proceedings of the Royal Society of London:Series A, 2008, 464: 273–288. DOI:10.1098/rspa.2007.1908 |
| [2] | Vukobratovic M, Herr H M, Borovac B, et al. Biological principles of control selection for a humanoid robot's dynamic balance preservation[J]. International Journal of Humanoid Robotics, 2008, 5(3): 639–678. |
| [3] | Tang Q, Xiong R, Chu J. Tip over avoidance control for biped robot[J]. Robotica, 2009, 27(6): 883–889. DOI:10.1017/S0263574708005298 |
| [4] | Park I W, Kim J Y, Oh J H. Online walking pattern generation and its application to a biped humanoid robot:KHR-3(HUBO)[J]. Advanced Robotics, 2008, 22(2/3): 159–190. |
| [5] | Vanderborght B, Verrelst B, Ham R V, et al. Objective locomotion parameters based inverted pendulum trajectory generator[J]. Robotics and Autonomous Systems, 2008, 56(9): 738–750. DOI:10.1016/j.robot.2008.01.003 |
| [6] | Kwon O, Park J H. Asymmetric trajectory generation and impedance control for running of biped robots[J]. Autonomous Robots, 2009, 26(1): 47–78. DOI:10.1007/s10514-008-9106-7 |
| [7] | Capi G, Yokota M. Optimal multi-criteria humanoid robot gait synthesis:an evolutionary approach[J]. International Journal of Innovative Computing, Information and Control, 2006, 2(6): 1249–1258. |
| [8] | Harada K, Kajita S, Kaneko K, et al. Dynamics and balance of a humanoid robot during manipulation tasks[J]. IEEE Transactions on Robotics, 2006, 22(3): 568–575. DOI:10.1109/TRO.2006.870649 |
| [9] |
付成龙, 陈恳.
五杆四驱动平面双足机器人动态步态规划与非线性控制[J]. 机器人, 2006, 28(2): 206–212.
FU Chenglong, CHEN Ken. Gait planning and nonlinear control of dynamic walking for a five-link, four-actuator, planar biped robot[J]. Robot, 2006, 28(2): 206–212. (in Chinese) |
| [10] | Chevallereau C, Grizzle J W, Shih C L. Asymptotically stable walking of a five-link underactuated 3-D bipedal robot[J]. IEEE Transactions on Robotics, 2009, 25(1): 37–50. DOI:10.1109/TRO.2008.2010366 |
| [11] | Grizzle J W, Abba G, Plestan F. Asymptotically stable walking for biped robots:analysis via systems with impulse effects[J]. IEEE Transactions on Automatic Control, 2001, 46(1): 51–64. DOI:10.1109/9.898695 |
| [12] | Plestan F, Grizzle J W, Westervelt E R, et al. Stable walking of a 7-DOF biped robot[J]. IEEE Transactions on Robotics, 2003, 19(4): 653–668. DOI:10.1109/TRA.2003.814514 |
| [13] | Jordan K, Challis J H, Cusumano J P, et al. Stability and the time-dependent structure of gait variability in walking and running[J]. Human Movement Science, 2009, 28(1): 113–128. DOI:10.1016/j.humov.2008.09.001 |
| [14] | 李祖枢. 仿人智能控制理论与多级摆的摆起控制[M]//涂序彦. 人工智能: 回顾与展望. 北京: 科学出版社, 2006: 174-207. |
| [15] | Li Z S, Wang G P. Schema theory and human simulated intelligent control[C]//Proceedings of the 2003 IEEE International Conference on Robotics, Intelligent Systems and Signal Processing, October 8-13, 2003, Changsha, Hunan, China. Piscataway:IEEE Press, 2003, 1:524-530. |
| [16] | 付成龙. 平面双足机器人的截面映射稳定性判据与应用[D]. 北京: 清华大学博士学位论文, 2006. |
 2013, Vol. 36
2013, Vol. 36

