1b. 重庆大学 山地城镇建设与新技术教育部重点实验室, 重庆 400045;
2. 后勤工程学院 建筑工程系, 重庆 400041
1b. Key Laboratory of New Technology for Construction of Cities in Mountain Area, Ministry of Education, Chongqing University Chongqing, 400045, China;
2. Department of Architecture & Civil Engineering, LEU, Chongqing, 400041, China
小净距隧道是指隧道间的中间岩柱厚度小于某一建议值的特殊隧道布置形式[1],由于小净距隧道在复杂地质条件下能够较好的衔接桥隧,实现总体线形优化和合理利用土地资源[2],在中国高速发展的公路网、铁路网建设中,修建了大量的浅埋小净距隧道。但从小净距隧道设计图纸可知,各隧道间支护参数千差万别,即使在相近的地质和地形情况下,隧道间的设计参数各不相同,这与小净距隧道的围岩压力计算是息息相关的[3-4]。
小净距隧道根据地形、地质情况,可分为浅埋非偏压和偏压小净距隧道。其中浅埋非偏压小净距隧道的围岩压力计算理论经过肖明清[5]、龚建武,夏才初[6]、喻军[7]等在试验和现场监测的基础上取得了一定的研究成果。而浅埋偏压小净距隧道进一步又可分为浅埋单侧偏压小净距隧道和浅埋双侧偏压小净距隧道。舒志乐,刘保县[8]、沈习文,邓荣贵[9]、彭琦,李亮[10]、刘元峰[11]等在公路设计规范的基础上,对浅埋单侧偏压小净距隧道的围岩压力计算理论进行推导,建立了相应的理论体系。而目前在西部海拔较高地区出现了大量的浅埋双侧偏压小净距隧道,该类型隧道由于受地形、地质情况的制约,受力情况更加复杂。但尚未建立该类型隧道的围岩压力计算理论,若采用浅埋非偏压或单侧偏压小净距隧道围岩压力计算理论进行计算,其结果将偏于保守,难以指导工程设计与施工。
笔者参照现有的公路设计规范,在国内外学者获得的学术成果的基础上,进一步考虑小净距隧道左右洞先后施工的相互作用,对浅埋双侧偏压小净距隧道的围岩压力计算理论进行探讨。
1 围岩压力计算公式推导 1.1 基本假定1) 岩(土)体为连续均匀介质,各向同性。隧道左侧地表倾角为αl,右侧地表倾角为αr,隧道左、右洞结构对称且在水平向平行布置,左、右洞按先后顺序开挖,不考虑仰拱对隧道的影响。
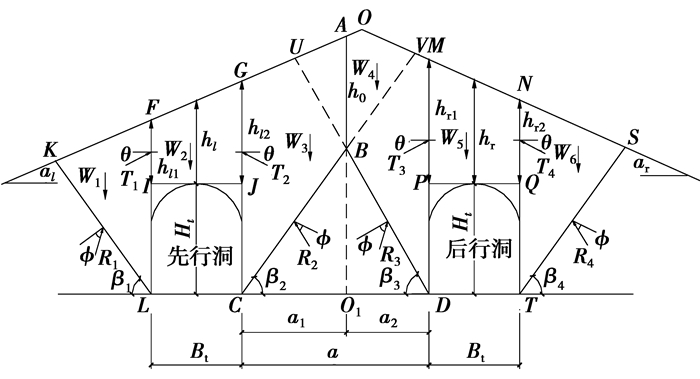
2) 先行洞开挖时,在先行洞外侧岩(土)体中形成与水平面成β1角的破裂面LK,在内侧形成与水平面成β2角的破裂面CV。当后行洞开挖时,后行洞外侧形成与水平面成β4角的破裂面TS,内侧为与水平面成β3角的破裂面DU,且与斜直面CV相交于隧道中岩柱处B点,由于隧道非对称偏压,岩柱中形成的破裂面的交点偏离中岩柱中心线一定距离,计算模型见图 1。
|
图 1 双侧偏压小净距隧道假定滑裂模式及计算简图 |
3) 分析多边形UBVOA,根据隧道开挖后岩(土)体的运动趋势,在多边形内竖直面AB处会产生张性破裂面,则后行洞内侧滑裂面变为ABD。由土力学理论可知,滑裂面AB的法向相互作用力必小于静止土压力,则假定滑裂面AB的法向作用力为0,此假定偏于安全。
4) 根据山体变形及两洞先后开挖后岩(土)体运动规律,假设隧道顶上覆土柱FIJG和MPNQ分别下沉,从而分别带动两侧土体LFK、CVG、TSN、DMOU下沉。T1,T2,T3,T4为左右洞两侧岩(土)体对拱顶下沉土柱施加的摩擦阻力,分析时考虑了内聚力c的影响,采用计算摩擦角φc。由于FI、GJ、MP、NQ并非实际破裂面,其滑面阻力小于破裂面阻力,该滑面的摩擦角为θ值,小于土体值φ,θ值按规范[1]选取。
1.2 围岩压力计算设隧道左侧地表倾角为αl,右侧地表倾角为αr,隧道净宽为Bt,净高为Ht,左洞左侧埋深为hl1, 右侧埋深为hl2,右洞左侧埋深为hr1, 右侧埋深为hr2,隧道左右洞净距为a,h0为左右洞内侧滑裂面交点至地表的垂直距离。
1) 先行洞开挖时围岩压力计算
先行洞开挖时,隧道内外侧围岩压力的计算可以采用规范中单洞偏压隧道围岩压力计算方法,其计算如下:
① 隧道侧向水平压力
假定偏压分布图形与地面坡一致,隧道内外侧的侧压力系数按下式计算
| $ {\lambda _1} = \frac{{\frac{{\left( {\tan {\beta _1} - \tan {\varphi _{\rm{c}}}} \right)}}{{\left( {\tan {\beta _1} - \tan {\alpha _{\rm{l}}}} \right)}}}}{{1 + \tan {\beta _1}\left( {\tan {\varphi _{\rm{c}}} - \tan \theta } \right) + \tan {\varphi _{\rm{c}}}\tan \theta }}, $ | (1) |
| $ tan{\beta _1} = \tan {\varphi _{\rm{c}}} + \sqrt {\frac{{\left( {{{\tan }^2}{\varphi _{\rm{c}}} + 1} \right)\left( {\tan {\varphi _{\rm{c}}} + \tan {\alpha _{\rm{l}}}} \right)}}{{\tan {\varphi _{\rm{c}}} - \tan \theta }}} , $ | (2) |
| $ {\lambda _2} = \frac{{\frac{{\left( {\tan {\beta _2} - \tan {\varphi _{\rm{c}}}} \right)}}{{\left( {\tan {\beta _2} - \tan {\alpha _{\rm{l}}}} \right)}}}}{{1 + \tan {\beta _2}\left( {\tan {\varphi _{\rm{c}}} - \tan \theta } \right) + \tan {\varphi _{\rm{c}}}\tan \theta }}, $ | (3) |
| $ tan{\beta _2} = \tan {\varphi _{\rm{c}}} + \sqrt {\frac{{\left( {{{\tan }^2}{\varphi _{\rm{c}}} + 1} \right)\left( {\tan {\varphi _{\rm{c}}} - \tan {\alpha _{\rm{l}}}} \right)}}{{\tan {\varphi _{\rm{c}}} - \tan \theta }}} , $ | (4) |
式中:β1,β2为外侧、内侧产生最大推力时的破裂角。
先行洞外侧、内侧水平压力为
| $ 外侧:{e_{{\rm{l}}1}} = {\lambda _1}\gamma {h_i}, $ | (5) |
| $ 内侧:{e_{{\rm{l}}2}} = {\lambda _2}\gamma {h_j}, $ | (6) |
式中:hi,hj为计算点至地表的垂直距离。
② 隧道拱顶垂直压力
假定偏压分布图形与地面坡一致,则
| $ {Q_1} = \frac{\gamma }{2}\left[ {\left( {{h_{{\rm{l1}}}} + {h_{{\rm{l2}}}}} \right){B_{\rm{t}}} - \left( {{\lambda _1}h_{{\rm{l1}}}^2 + {\lambda _1}h_{{\rm{l2}}}^2} \right)\tan \theta } \right], $ | (7) |
式中:hl1,hl2为先行洞外、内侧由拱顶至地面的高度, m。
由式(7)可得
| $ {q_{le}} = \frac{\gamma }{2}\left[ {\left( {{h_{{\rm{l1}}}} + {h_{{\rm{l2}}}}\left( { - \frac{{\left( {{\lambda _1}h_{{\rm{l1}}}^2 + {\lambda _2}h_{{\rm{l2}}}^2} \right)\tan \theta }}{{{B_t}}}} \right.} \right.} \right], $ | (8) |
| $ \left. \begin{array}{l} {q_1} = {q_{le}} - \frac{{{B_{\rm{t}}}}}{2}\tan {\alpha _{\rm{l}}}\\ {q_2} = {q_{le}} + \frac{{{B_{\rm{t}}}}}{2}\tan {\alpha _{\rm{l}}} \end{array} \right\}。$ | (9) |
2) 后行洞开挖时围岩压力计算
① 后行洞外侧侧向水平压力
后行洞开挖时,后行洞外侧侧向水平压力计算与先行洞外侧水平压力计算原理相同,则
| $ {\lambda _4} = \frac{{\frac{{\left( {\tan {\beta _4} - \tan {\varphi _{\rm{c}}}} \right)}}{{\left( {\tan {\beta _4} - \tan {\alpha _{\rm{r}}}} \right)}}}}{{1 + \tan {\beta _4}\left( {\tan {\varphi _{\rm{c}}} - \tan \theta } \right) + \tan {\varphi _{\rm{c}}}\tan \theta }}, $ | (10) |
| $ tan{\beta _4} = \tan {\varphi _{\rm{c}}} + \sqrt {\frac{{\left( {{{\tan }^2}{\varphi _{\rm{c}}} + 1} \right)\left( {\tan {\varphi _{\rm{c}}} + \tan {\alpha _{\rm{r}}}} \right)}}{{\tan {\varphi _{\rm{c}}} - \tan \theta }}} , $ | (11) |
式中β4为后行洞外侧产生最大推力时的破裂角。
外侧向水平压力
| $ {e_{r2}} = {\lambda _4}\gamma {h_i}, $ | (12) |
式中hj为计算点至地表的垂直距离。
② 后行洞内侧侧向水平压力
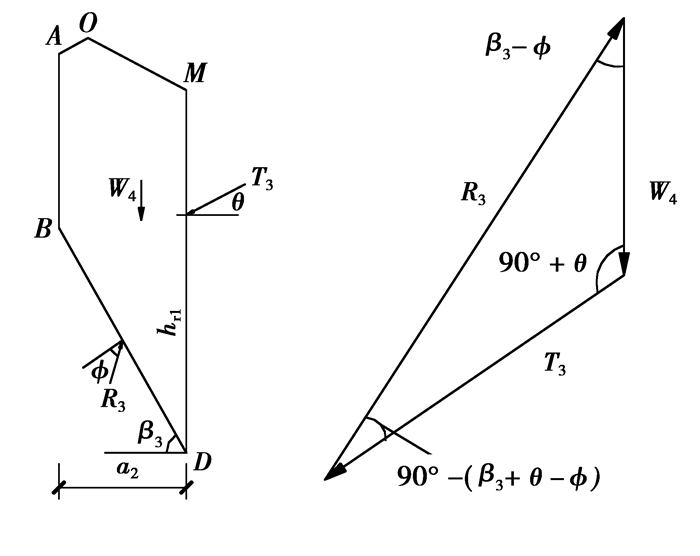
后行洞内侧侧压力计算时,对隔离体ABDMO进行受力分析,其计算简图如图 2所示。
|
图 2 后行洞开挖时内侧侧压力计算简图 |
根据前述假定及力的平衡原理,可得
| $ \begin{array}{*{20}{c}} {{T_3} = \frac{{\sin \left( {{\beta _3} - {\varphi _{\rm{c}}}} \right)}}{{\sin \left[ {{{90}^ \circ } - \left( {{\beta _3} - {\varphi _{\rm{c}}} + \theta } \right)} \right]}}{W_4} = }\\ {\frac{{\gamma {a_2}\left[ {{h_{{\rm{r1}}}} + {H_{\rm{t}}} + {h_0}} \right]\sin \left( {{\beta _3} - {\varphi _{\rm{c}}}} \right)}}{{2\sin \left[ {{{90}^ \circ } - \left( {{\beta _3} - {\varphi _{\rm{c}}} + \theta } \right)} \right]}},} \end{array} $ | (13) |
经整理后
| $ {T_3} = \frac{1}{2}\gamma h_{{\rm{r1}}}^2\frac{{{\lambda _3}}}{{\cos \theta }}, $ | (14) |
其中
| $ {\lambda _3} = \frac{{\frac{{{a_2}}}{{h_{{\rm{r1}}}^2}}\left[ {{h_{{\rm{rl}}}} + {H_{\rm{t}}} + {h_0}} \right]\left( {\tan {\beta _3} - \tan {\varphi _{\rm{c}}}} \right)}}{{1 + \tan {\beta _3}\left( {\tan {\varphi _{\rm{c}}} - \tan \theta } \right) + \tan {\varphi _{\rm{c}}}\tan \theta }}, $ | (15) |
式中λ3为后行洞内侧侧向水平压力系数。
为使得T3取极大值,令
| $ \begin{array}{l} \tan {\beta _3} = \frac{{\left( {\tan {\varphi _{\rm{c}}} - \tan \theta } \right)}}{{2\left( {\tan {\varphi _{\rm{c}}} - \tan \theta } \right)}} + \\ \frac{{\sqrt { - 4\left( {1 + {{\tan }^2}{\varphi _{\rm{c}}}} \right)\left( {\tan {\varphi _{\rm{c}}} - \tan \theta } \right) + {{\left( {\tan {\varphi _{\rm{c}}} - \tan \theta } \right)}^2}} }}{{2\left( {\tan {\varphi _{\rm{c}}} - \tan \theta } \right)}}, \end{array} $ | (16) |
式中β3为产生最大推力T3时的破裂角。
后行洞内侧侧向水平压力er1为
| $ {e_{r1}} = {\lambda _3}\gamma {h_i}, $ | (17) |
式中hi为计算点至地表的垂直距离。
③ 后行洞拱顶垂直压力
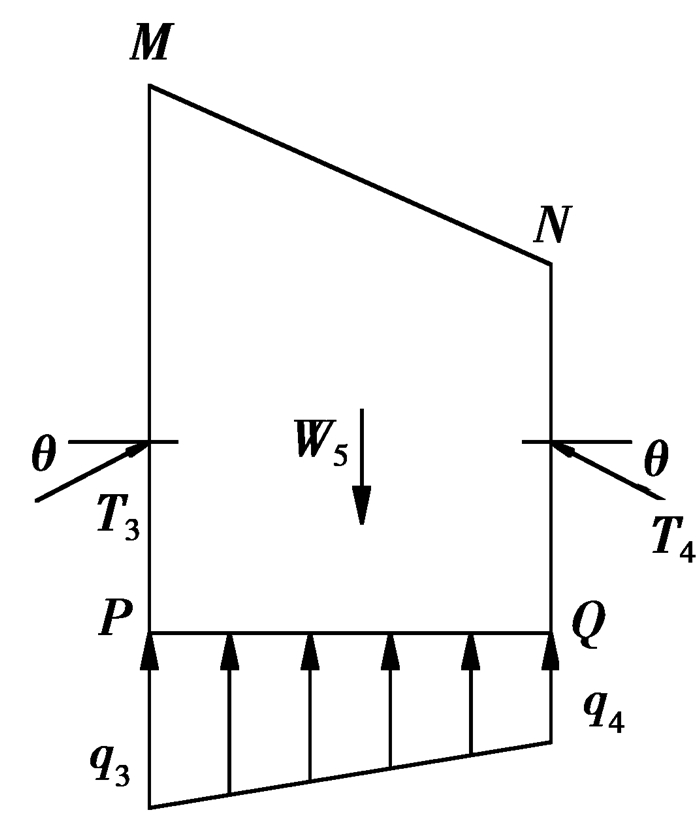
设作用于后行洞顶部的垂直压力内侧为q3,外侧为q4,内外侧之间按线性变化,其计算简图如图 3所示。
|
图 3 后行洞拱顶围岩体受力计算简图 |
| $ {Q_r} = {W_5} - {T_3}\sin \theta - {T_4}\sin \theta , $ | (18) |
换算为作用在后行洞拱顶支护结构上的均布荷载为
| $ {q_{re}} = \frac{{{W_5} - {T_3}\sin \theta - {T_4}\sin \theta }}{{{B_t}}} = $ | (19) |
| $ \frac{1}{2}\gamma \left[ {\left( {{h_{{\rm{r1}}}} + {h_{{\rm{r2}}}}} \right) - \frac{{\tan \theta }}{{{B_t}}}\left( {{\lambda _3}h_{{\rm{r1}}}^2 + {\lambda _4}h_{{\rm{r2}}}^2} \right)} \right], $ | (20) |
| $ \left. \begin{array}{l} {q_3} = {q_{re}} + \frac{{{B_t}}}{2}\tan {\alpha _{\rm{r}}}\\ {q_4} = {q_{re}} - \frac{{{B_t}}}{2}\tan {\alpha _{\rm{r}}} \end{array} \right\}。$ | (21) |
3) 后行洞开挖后先行洞围岩压力
① 后行洞开挖后先行洞侧向水平压力
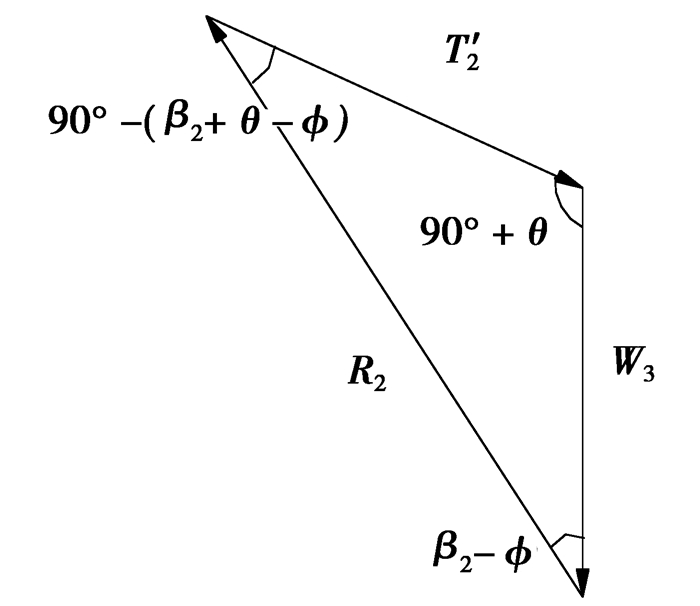
后行洞开挖后,先行洞外侧围岩压力基本保持不变,其侧向水平压力计算仍按式(5)进行。而内侧围岩压力发生变化,取隔离体ABCG进行受力分析,如图 4所示。
|
图 4 隔离体ABCG受力分析图 |
| $ \begin{array}{l} {{T'}_2} = \frac{{\sin \left( {{\beta _2} - {\varphi _{\rm{c}}}} \right)}}{{\sin \left[ {{{90}^ \circ } - \left( {{\beta _3} - {\varphi _{\rm{c}}} + \theta } \right)} \right]}}{W_3} = \\ \;\;\;\;\;\;\;\frac{{\gamma {a_1}\left[ {{h_{12}} + {H_{\rm{t}}} + {h_0}} \right]\sin \left( {{\beta _2} - {\varphi _{\rm{c}}}} \right)}}{{2\sin \left[ {{{90}^ \circ } - \left( {{\beta _2} - {\varphi _{\rm{c}}} + \theta } \right)} \right]}}, \end{array} $ | (22) |
经整理得
| $ {{T'}_2} = \frac{1}{2}\gamma h_{12}^2\frac{{{{\lambda '}_2}}}{{\cos \theta }}, $ | (23) |
其中
| $ {{\lambda '}_2} = \frac{{\frac{{{a_1}}}{{h_{{\rm{l}}2}^2}}\left[ {{h_{{\rm{l2}}}} + {H_{\rm{t}}} + {h_0}} \right]\left( {\tan {\beta _2} - \tan {\varphi _{\rm{c}}}} \right)}}{{1 + \tan {\beta _2}\left( {\tan {\varphi _{\rm{c}}} - \tan \theta } \right) + \tan {\varphi _{\rm{c}}}\tan \theta }}, $ | (24) |
式中λ′2为后行洞开挖后先行洞内侧侧向水平压力系数,其中β2按式(4)计算。
先行洞内侧侧向水平压力e′l2为
| $ {{e'}_{{\rm{l2}}}} = {{\lambda '}_2}\gamma {h_i}, $ | (25) |
式中hi为计算点至地表的垂直距离。
② 后行洞开挖后先行洞拱顶垂直压力
类似于前面计算,可得先行洞拱顶内外侧垂直压力q1和q′2为
| $ {q_{le}} = \frac{\gamma }{2}\left[ {\left( {{h_{{\rm{l1}}}} + {h_{{\rm{l2}}}}} \right) - \frac{{\tan \theta }}{{{B_t}}}\left( {{\lambda _2}h_{{\rm{l1}}}^2 + {{\lambda '}_2}h_{{\rm{l2}}}^2} \right)} \right], $ | (26) |
| $ \left. \begin{array}{l} {{q'}_1} = {q_{le}} - \frac{{{B_{\rm{t}}}}}{2}\tan {\alpha _1}\\ {{q'}_2} = {q_{le}} + \frac{{{B_{\rm{t}}}}}{2}\tan {\alpha _1} \end{array} \right\}。$ | (27) |
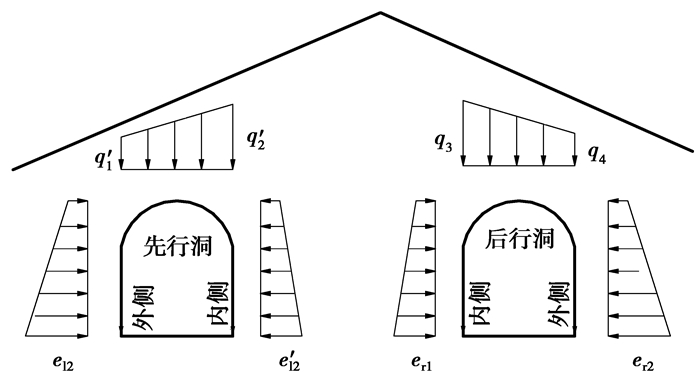
由上述理论推导可得,浅埋双侧偏压小净距隧道开挖后先行洞与后行洞围岩压力分布如图 5所示。
|
图 5 双侧偏压小净距隧道围岩压力分布图 |
钻前门隧道位于山西省忻保高速G1段,为双向四车道,是一座典型的浅埋双侧偏压小净距隧道。隧道左线起止桩号为ZK30+045~ZK30+316,长271 m;隧道右线起止桩号为YK30+050~YK30 +315,长265 m,如图 6所示。隧道浅埋偏压段主要为全~强风化片麻岩,围岩级别为V级,容重为20 kN/m3。文中选取K30+100断面进行分析,隧道左洞埋深为22.60 m,右洞埋深为17.44 m,左右洞净距为16.5 m。隧道单洞开挖宽度Bt为12.56 m,隧道高度Ht为8.84 m。隧道左侧地表倾角为32°,右侧地表倾角为25°。

|
图 6 钻前门隧道 |
为了研究浅埋双侧偏压小净距隧道围岩与初期支护间接触压力分布情况,在隧道里程为K30+100断面布置了一批振弦式围岩压力计监测点,现场测点安装及布置如图 7所示。

|
图 7 围岩压力测点安装及布置示意图 |
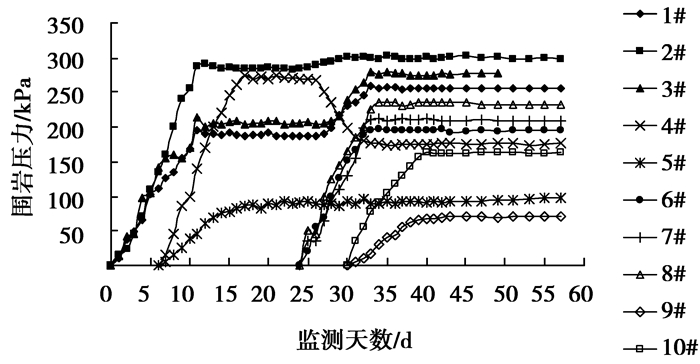
该隧道在K30+100断面的围岩与初期支护间接触压力现场监测结果见图 8所示,左、右洞均采用上下台阶法开挖,右洞滞后左洞24 d开挖。
|
图 8 围岩与初期支护间接触压力随时间的关系图 |
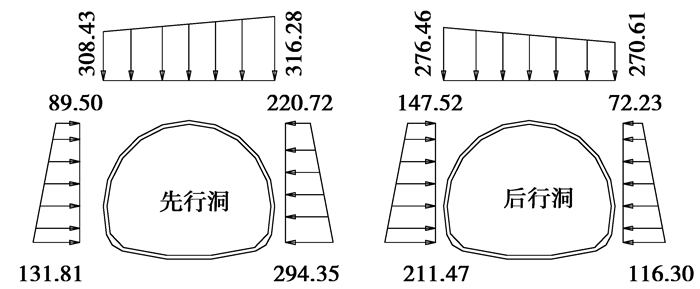
由公式(5)、(12)、(17)、(21)、(25)、(27)可求得钻前门隧道K30+100断面的竖直围岩压力和侧向水平围岩压力值,见图 9所示。
|
图 9 钻前门隧道围岩压力理论计算值(kPa) |
由图 8监测结果可知,隧道左洞开挖后,由于受左侧地形偏压的影响,左洞右拱腰处接触压力最大,右边墙及左拱腰处次之。当右洞开挖时,左洞围岩与初期支护接触压力受影响较大,左洞右拱腰、左拱腰及拱顶处围岩压力值增大,而左洞右边墙处围岩压力减小,左边墙处围岩压力稍有增加,但增大值极小。受右侧地形偏压的影响,右洞左拱腰处围岩压力最大,右洞右拱腰处次之。
为了便于对理论计算值与现场监测值进行比较,将图 9中竖向围岩压力与侧向水平围岩压力进行矢量合成后作用于隧道洞周面上。隧道各关键点的围岩压力理论计算值与现场监测最终值经整理后如表 1所示。
| 表 1 隧道各关键点围岩压力理论计算值与监测值 |
由表 1可知,隧道各关键点围岩压力监测值比理论值偏小,究其原因:一是隧道现场监测测点布置滞后, 隧道开挖后围岩压力发生释放,前期释放值无法测出;二是理论计算是基于一系列假设和极限平衡理论的基础上建立的,而实际隧道不可能让围岩变形充分发展直至发生破坏,且隧道现场的地质及施工情况极其复杂。从各关键点围岩压力值大小和分布来看,监测值均小于理论值,且两者的分布规律相似,由此可知按此理论计算模型进行该类型隧道围岩压力的计算是可行的。
3 结论1) 浅埋双侧偏压小净距隧道围岩压力大小及分布规律与单侧偏压或非偏压隧道相比,具有独特的之处,左右洞内侧拱腰处围岩压力最大,外侧拱腰处次之,然后依次为拱顶处、内边墙处,外边墙处最小。
2) 从理论计算和现场监测可知,后行洞开挖对先行洞围岩压力分布具有一定的影响,先行洞右拱腰、左拱腰及拱顶处围岩压力值增大,而右边墙处围岩压力值减小,左边墙处围岩压力基本保持不变。该类型隧道设计时应重视左右洞开挖相互影响,避免隧道初期支护参数不足导致隧道发生大变形或坍塌。
3) 由于浅埋双侧偏压小净距隧道中间岩柱承担较大的竖向压力,尤其是在净距较小的情况下,应加强对中间岩柱的加固,确保隧道的整体稳定性。
| [1] | 中华人民共和国行业标准编写组. JTG D70-2004公路隧道设计规范[S]. 北京: 人民交通出版社, 2004. |
| [2] |
黄拔洲, 陈少华, 秦峰.
小净距隧道在京福高速公路上的实践[J]. 重庆大学学报:自然科学版, 2003, 26(10): 19–22.
HUANG Bazhou, CHEN Shaohua, QIN Feng. Development of parallel tunnels with super-small interval in Beijing-Fuzhou freeway engineering[J]. Journal of Chongqing University:Natural Science Edition, 2003, 26(10): 19–22. (in Chinese) |
| [3] | Sari Y D, Pasamehmetoglu A G, Cetiner E, et al. Numerical analysis of a tunnel support design in conjunction with empirical methods[J]. International Journal of Geomechanics, 2008, 8(1): 74–81. DOI:10.1061/(ASCE)1532-3641(2008)8:1(74) |
| [4] | Shao Y, Macari E J. Information feedback analysis in deep excavations[J]. International Journal of Geomechanics, 2008, 8(1): 91–103. DOI:10.1061/(ASCE)1532-3641(2008)8:1(91) |
| [5] |
肖明清.
小间距浅埋隧道围岩压力的探讨[J]. 现代隧道技术, 2004, 41(3): 7–10.
XIAO Mingqing. Study on the rock pressure acting on shallow tunnels with small spacing[J]. Modern Tunnelling Technology, 2004, 41(3): 7–10. (in Chinese) |
| [6] |
龚建伍, 夏才初, 雷学文.
浅埋小净距隧道围岩压力计算与监测分析[J]. 岩石力学与工程学报, 2010, 29(2): 4139–4145.
GONG Jianwu, XIA Caichu, LEI Xuewen. Analysis of field measurement and theoretical calculation on rock pressure in shallow-buried twin tunnels with small spacing[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(2): 4139–4145. (in Chinese) |
| [7] |
喻军, 刘松玉, 童立元.
小净距隧道设计荷载的确定[J]. 东南大学学报:自然科学版, 2008, 38(5): 856–860.
YU Jun, LIU Songyu, TONG Liyuan. Determination of designing load of small clear space tunnel[J]. Journal of Southeast University:Natural Science Edition, 2008, 38(5): 856–860. (in Chinese) |
| [8] |
舒志乐, 刘保县, 李月.
偏压小净距隧道围岩压力分析[J]. 地下空间与工程学报, 2007, 3(3): 430–433.
SHU Zhile, LIU Baoxian, LI Yue. Surrounding rock pressure analysis of neighbourhood tunnel under unsymmetrical pressure[J]. Chinese Journal of Underground Space and Engineering, 2007, 3(3): 430–433. (in Chinese) |
| [9] | 沈习文. 小净距偏压公路隧道围岩压力分析[D]. 四川: 西南交通大学硕士学位论文, 2007. |
| [10] | 彭琦. 浅埋偏压小净距隧道围岩压力及施工力学研究[D]. 长沙: 中南大学硕士学位论文, 2008. |
| [11] | 刘元锋. 米家寨隧道施工力学及其空间效应研究[D]. 重庆: 重庆大学硕士学位论文, 2010. |
 2013, Vol. 36
2013, Vol. 36

