b. 重庆大学 软件学院, 重庆 400044
b. College of Software Engineering, Chongqing University, Chongqing 400044, China
在电力系统负荷预测实际工作中,由于SCADA系统中的量测、记录、转换、传输等任意环节故障都可能导致观测数据出现反常态势,以致与大多数观测值不一致;另一方面,由于特殊事件(如线路检修停电,切负荷停电,大事件冲击等)而引起负荷的异常变化,也会导致观测数据违背常规。所有这些非正常的负荷观测数据统称为坏数据。如果直接采用含有坏数据的原始负荷数据进行电力负荷建模与负荷预测,其预测结果的准确度将无法保障,因此在进行预测工作之前需要对原始负荷数据进行预处理[1],剔除其中的坏数据。
目前对于负荷数据中的坏数据的辨识以及修正已经提出了多种方法。文献[2]中分别计算历史数据中各日同时刻的负荷,确定其变化率范围,再以此对比检测日同时刻的负荷变化率确定该点异常与否。但是该方法仍然存在不足,主要在于其虽然对于单个坏数据的识别比较有效,但是如果数据第一点是坏数据或者坏数据连续产生时,该方法容易产生漏判或误判。文献[3]中采用在灰色估计中引入了参数估计法,以此为模型对坏数据进行辨识,但是参数估计是非线性优化问题,由于其所具有的复杂性,导致该方法计算速率较慢,且容易陷入局部极值。在文献[1]中提出了用神经网络辨识坏数据并给予调整,能有效地实现坏数据的定位,但是该方法仍然有两个缺陷:一是该方法中所采用的Kohonen神经网络[4]只能实现球形数据的硬聚类,以此为基准来调整坏数据比较粗糙;二是因为BP神经网络[4-6]所固有的特性,无法从根本上避免陷入局部极小。针对传统负荷预测中数据预处理的不足,本文提出了基于加权核函数模糊C均值聚类算法(weighing Kernel-based Fuzzy C-means clustering-WKFCM)结合超圆神经元网络的数据辨识修正模型,有效提高了数据预处理的精度。
1 负荷坏数据聚类算法如果不剔除和修正原始负荷数据中的坏数据,那么它们将以伪信息、伪变化规律的方式提供给负荷预测作为参考,必然影响预测结果的精确度及可靠性。在原始负荷数据中,坏数据的产生往往是随机的。虽然有些坏数据可以通过分析数据的物理意义进行剔除和修正,比如线路检修停电、切负荷停电、大事件冲击等可以从事件发生的时间来分离正常数据和坏数据,但这种方法效率低,且对于数据采集、传输过程中产生的坏数据无法剔除和修正。
如何辨识与修正这些坏数据是必须要考虑的首要问题。电力负荷曲线具有明显的周期性、平滑性和相似性特点,对坏数据进行辨识的第一步就是对原始负荷数据进行聚类分析[7-11],提取负荷的特征曲线。
作为目前研究应用最广泛的聚类算法,模糊C均值聚类算法(Fuzzy C-means clustering-FCM)[9-10]本质上是一种局部搜索算法,整个算法的关键是求取目标函数极值点,该点为聚类中心和数据点之间的距离加权和,从而得到聚类中心的迭代公式,该算法通过构造拉格朗日函数,迭代求取各样本到聚类中心的全局加权距离平方和最小值以获得最优聚类中心。
FCM算法是个体属于某聚类的程度或计算隶属度的一种算法,将N个个体xk(k=1, 2, ……, n)分为c个模糊类,分别计算类的聚类中心,使其类内加权误差平方和达到最小。FCM算法和硬C均值聚类算法之间的主要区别为FCM算法采用模糊划分,计算每个给定数据点的隶属度,以此确定该数据点属于各组的程度,为了和模糊划分适应,设定隶属矩阵U取值范围为[0, 1]间,进行标准化以后,每个个体的隶属度总和均为1
| $ \sum\limits_{i = 1}^c {{\mu _{ik}}} = 1,k = 1,2, \cdots ,n。$ | (1) |
目标函数为
| $ \min \left\{ {{J_m}\left( {U,V} \right)} \right\} = \min \left\{ {\sum\limits_{k = 1}^n {\sum\limits_{i = 1}^c {{{\left( {{\mu _{ik}}} \right)}^m}{{\left( {{d_{ik}}} \right)}^2}} } } \right\}。$ | (2) |
其中:μik∈[0, 1]表示第k个数据隶属于第i个聚类中心的程度;vi为模糊类的聚i类中心;dik为第k个聚类中心与第i个数据间的欧氏距离;m∈[0, 2]为一个加权指数,根据聚类准则构造拉格朗日函数
| $ F = \sum\limits_{i = 1}^c {{{\left( {{\mu _{ik}}} \right)}^m}{{\left( {{d_{ik}}} \right)}^2} + {\lambda _k}\left( {\sum\limits_{i = 1}^c {{\mu _{ik}}} - 1} \right)} 。$ | (3) |
上式中λk(k=1, 2, ……n)为拉格朗日乘子,若对所有输入参数求导得到目标函数最小,其必要条件如下
| $ {\mu _{ik}} = \frac{1}{{\sum\nolimits_{j = 1}^c {{{\left( {\frac{{{d_{ik}}}}{{{d_{jk}}}}} \right)}^{\frac{2}{{m - 1}}}}} }}, $ | (4) |
| $ {v_i} = \frac{{\sum\nolimits_{k = 1}^n {{{\left( {{\mu _{ik}}} \right)}^m}{x_k}} }}{{\sum\nolimits_{k = 1}^n {{{\left( {{\mu _{ik}}} \right)}^m}} }}。$ | (5) |
虽然FCM算法具有上述优点,但也存在着不足之处,主要是模式的线性可分概率较低,计算的复杂度较高[11-13]。针对这一问题,本文采用核诱导距离1-K(xk-vi)的简单两项和替代欧氏距离以此来提高线性可分概率,减小计算的复杂度。
则聚类目标公式相应变为
| $ J\left( {U,V} \right) = \sum\limits_{i = 1}^c {\sum\limits_{k = 1}^n {\mu _{ik}^m\left( {1 - K\left( {{x_k} - {v_i}} \right)} \right)} } 。$ | (6) |
另外为了表示各类的不同重要度,本文在目标公式的核函数中加入一个动态权值αi,该权值的意义是:在迭代过程中有的类元素较多,组织较为稠密,这样的类别相应的重要度也应更大,且所有元素隶属度相加之和也大;反之亦如此,该方法我们称为加权核函数模糊C均值聚类算法(WKFCM)。在聚类算法中加入动态权值可以为不同的类分配不同权值,以此来达到改善聚类的目的。
改进后的WKFCM算法的目标函数为
| $ {J_{Km}}\left( {U,V} \right) = \sum\limits_{i = 1}^c {\sum\limits_{k = 1}^n {\alpha _i^m\mu _{ik}^m\left( {1 - K\left( {{x_k} - {v_i}} \right)} \right)} } 。$ | (7) |
其中
| $ {{\hat v}_i} = \frac{{\sum\limits_{k = 1}^N {\mu _{ik}^mK\left( {{x_k},{v_i}} \right){x_k}} }}{{\sum\limits_{k = 1}^N {\mu _{ik}^mK\left( {{x_k},{v_i}} \right)} }}, $ | (8) |
| $ {{\hat a}_i} = \frac{{{{\left( {\sum\limits_{k = 1}^N {\mu _{ik}^md_{ik}^2\left( {{x_k},{{\hat v}_i}} \right)} } \right)}^{\frac{1}{{1 - m}}}}}}{{\sum\limits_{i = 1}^C {{{\left( {\sum\limits_{k = 1}^N {\mu _{ik}^md_{ik}^2\left( {{x_k},{{\hat v}_i}} \right)} } \right)}^{\frac{1}{{1 - m}}}}} }}, $ | (9) |
| $ {{\hat \mu }_{ik}} = \frac{{{a_i}{{\left( {1 - k\left( {{x_k} - {v_i}} \right)} \right)}^{\frac{1}{{1 - m}}}}}}{{\sum\limits_{i = 1}^C {{a_i}{{\left( {1 - k\left( {{x_k} - {v_i}} \right)} \right)}^{\frac{1}{{1 - m}}}}} }}。$ | (10) |
当max‖
| $ \begin{array}{*{20}{c}} {K\left( {{x_k} - {v_i}} \right) = \exp \left( { - {\sigma ^{ - 2}}{{\left\| {{x_k} - {v_i}} \right\|}^2}} \right);\sigma \in R,}\\ {且\;\sigma \ne 0。} \end{array} $ | (11) |
其中σ值的确定可由经验或者根据实验获取。
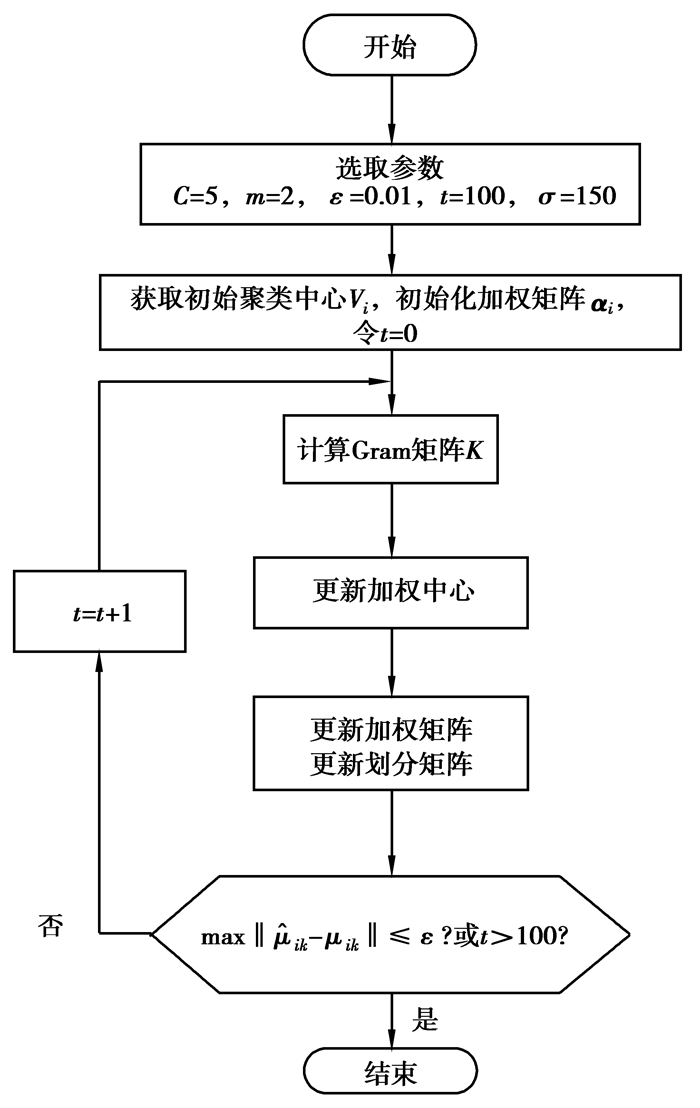
整个WKFCM聚类算法流程如图 1所示。
|
图 1 算法流程图 |
超圆神经元网络(Super circle covering artificial neural network-CC)[14-15]中的每一个神经元都具有一个吸引域。相同的响应输出在吸引域内对应于相同的输入数据。在神经元吸引域中的输入特征和相同的输出类别对应。
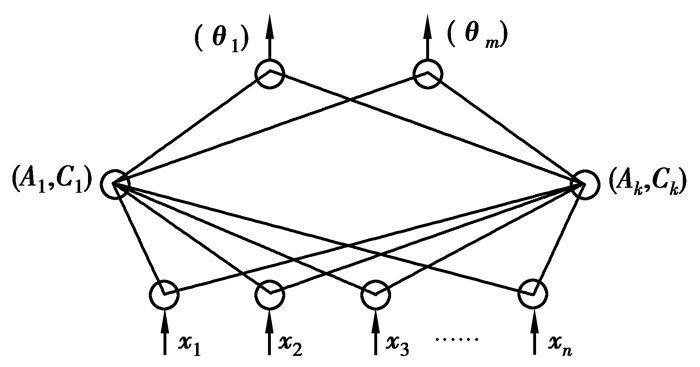
所以,CC模型是用非线性的方法对输入空间进行分割。下图是CC模型的网络结构,如图 2所示。其中第一层是指CC神经元层,它们的主要作用是完成对样本空间的划分,下面提到的算法确定其个数每个CC神经元的参数为(Ai, Ci),Ai表示的是特征向量,Ci表示的是吸引域。第二层是指MP神经元层,它的作用是完成对输出的判断,参数θ由每个MP神经元确定。CC神经元层的M个元件到MP神经元层的K个元件是全连接的,其权值定义如下
| $ \begin{array}{*{20}{c}} {{\omega _{mk}} = - \left( {y\left( {{A^m}} \right)} \right)k;\;\;\;{\theta _k} = - \sum\limits_m {{\omega _{mk}}} ,}\\ {\left( {m = 1,2, \cdots ,M;k = 1,2, \cdots ,K} \right)。} \end{array} $ | (12) |
|
图 2 基于CC模型的网络结构 |
仅需构造出CC网的训练样本集即可完成对CC网的训练。根据上节中WKFCM聚类算法根据聚类中心将负荷曲线划分成P类,分别标记为X1, X2, …, XP,则基于CC网络的辨识模型的样本集训练如下所示。
1) 样本输入选择特征曲线X1,其样本输出Y为(0, …, 0)。
2) 将一个偏差e叠加到X1的第一个分量, 于是产生了一条曲线,该曲线含有1个坏数据,对应的输出Y为(1, 0, …, 0)。然后依次对第二个直至全部分量均如此处理, 最终得到正偏差的样本集。
3) 把e换成-e,+1换成-1,重复上面第2) 步,这样得到了负偏差样本集,从而形成CC1的样本集,从而第i个CC模型的训练数据样本集就得到了。
按照上面的步骤方法就可以形成CC2,…, CCp的输入和输出样本集,从而得到所有模型的坏数据集。本文把曲线的横向特征作为主要考虑对象,通常对坏数据的直观判断方法是对识别一些使曲线突变和破坏的曲线。CC模型训练结束后,将本类型中任意一条负荷曲线输入网络。这样包含了坏数据的输出将会接近1,相对的正常点的输出接近0。对于任何种类模型的坏数据都能进行定位与辨识。
3 坏数据修正采用WKFCM算法对历史负荷数据进行聚类后,得到5条特征曲线,通过超圆神经网络对坏数据进行辨识,找到电力负荷样本中的坏数据,并对检测出来的坏数据进行修正,以免这些坏数据影响负荷预测的精度。
设曲线xj的t1点到t2点之间的数据为坏数据,它的隶属度中最大的两个类中心分别为vi1和vi2,在采用下列公式对坏数据进行修正
| $ {{x'}_j}\left( t \right) = {{\nu '}_{il}}\left( t \right)\frac{{{u_{i1,j}}}}{{{u_{i1,j}} + {u_{i2,j}}}} + {{\nu '}_{i2}}\left( t \right)\frac{{{u_{i2,j}}}}{{{u_{i1,j}} + {u_{i2,j}}}}, $ | (13) |
| $ {{\nu '}_{il}}\left( t \right) = {\nu _{il}}\left( t \right) \times \left( {\frac{{{x_j}\left( {{t_1} - 1} \right)}}{{{\nu _{i1}}\left( {{t_1} - 1} \right)}} + \frac{{{x_j}\left( {{t_2} + 1} \right)}}{{{\nu _{i1}}\left( {{t_2} + 1} \right)}}} \right)/2, $ | (14) |
| $ {{\nu '}_{i2}}\left( t \right) = {\nu _{i2}}\left( t \right) \times \left( {\frac{{{x_j}\left( {{t_1} - 1} \right)}}{{{\nu _{i2}}\left( {{t_1} - 1} \right)}} + \frac{{{x_j}\left( {{t_2} + 1} \right)}}{{{\nu _{i2}}\left( {{t_2} + 1} \right)}}} \right)/2。$ | (15) |
式中t∈[t1, t2];νi1,j、νi2,j、分别表示数据矢量xj对类中心νi1、νi2的隶属度值。
经过上面式子的调整,可以得到修正后的曲线xj,从经过修正之后的曲线和本类曲线更加吻合,而且即使有个别正常数据被误检为坏数据,来用上述公式进行修正后其结果也不会产生大的误差。
4 实例分析根据所提出坏数据辨识调整智能模型,用四川某电业局2010年1月1日至2月28日工作日的实际负荷数据为依据,对上述模型进行训练。
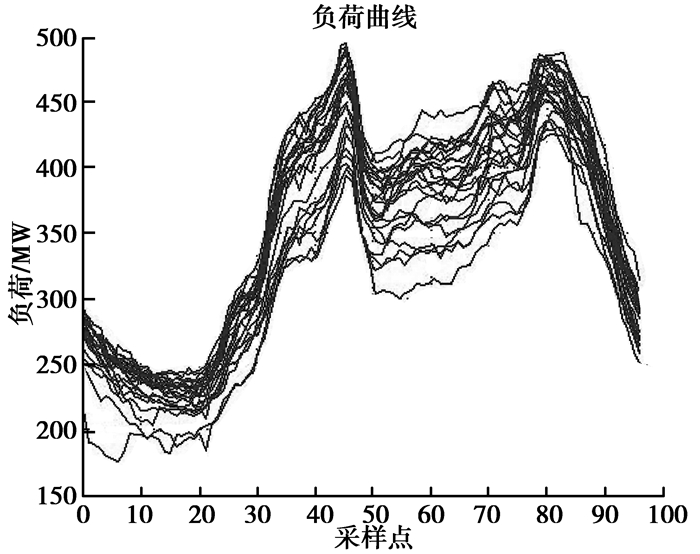
在提出的模型中,应在合理的区间内选取聚类中心数c。因为如果c值过小,整个聚类过程比较粗糙,修正误差也比较大;反之如果c过大,模型的计算量会大大增加,聚类也变得毫无意义。在实际工作中我们分析发现。2010年1月1日至2月28日工作的数据虽然数值大小差别较大,但是各负荷曲线在形状上却非常相似(见图 3)。
|
图 3 2010年1月1日至2月28日负荷曲线 |
由于所提出的模型都是利用负荷曲线的相似性与平滑性来实现坏数据的处理。为了使得特征曲线具有更强的代表性,且进一步消除负荷水平的影响,需要对负荷数据进行归一化处理。
采用归一化公式
| $ {{x'}_j}\left( i \right) = \frac{{{x_j}\left( t \right)}}{{\sum\limits_{i = 1}^q {{x_j}\left( i \right)} }}。$ | (16) |
上式中xj代表一天的实际负荷;q表示每天的采样数目,每天取96个数据,i=1, 2, …, 96。
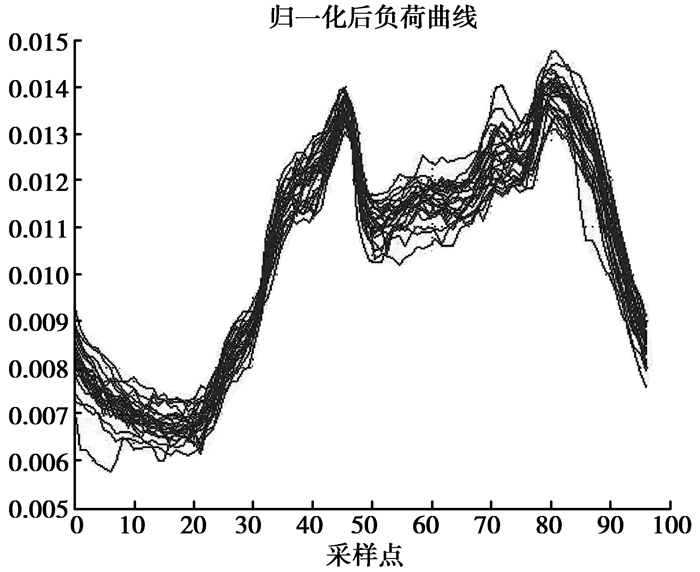
从图 4可以看出,经过归一化后,各曲线的形状都十分相似,在多次试验的基础上,我们发现把聚类中心数的取值为5能够准确地反映各曲线的特征。另外对图 4仔细观察可以看出,没有经过修正的曲线仍然有不少表示坏数据的毛刺。
|
图 4 2010年1月1日至2月28日的负荷归一化后的曲线 |
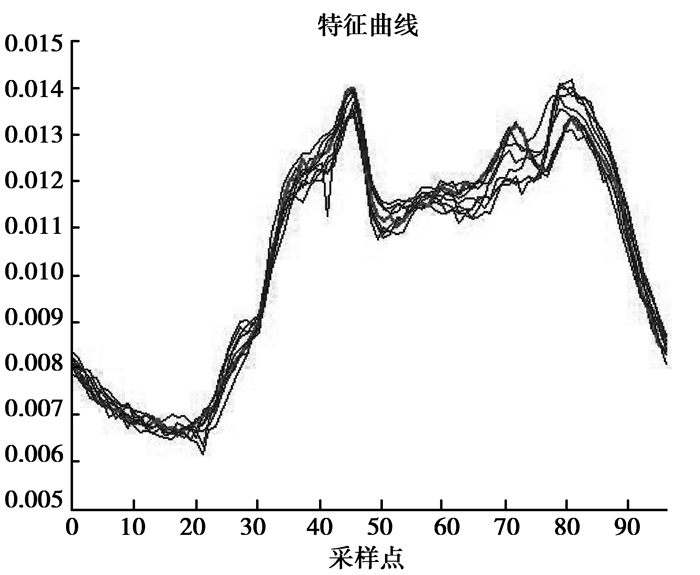
在MATLAB中通过随机选取出一条特征曲线和隶属于该曲线的负荷曲线经过归一后的图像来表现出更好的聚类分析效果,如图 5所示。
|
图 5 归一化后的某类曲线及其特征曲线 |
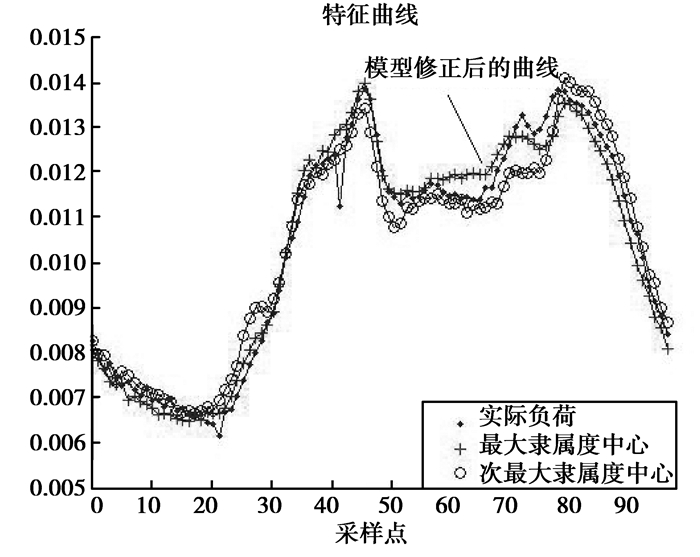
从图 5可以看出,可以发现明显的代表坏数据的尖刺,并且可以发现正常曲线和中心两者之间的距离非常小。为了验证本文所述修正方法的有效性,将含有坏数据的负荷曲线以及该曲线的最大特征中心曲线、次大特征中心曲线与修正后的曲线负荷输出进行比较分析,结果如图 6所示。
|
图 6 对含有坏数据曲线的检测 |
从图 6可以看出,聚类曲线对坏数据的辨识以及修正的效果是令人满意的。随机抽取训练集中和训练集外某月的历史负荷数据进行检验,检验结果如表 1所示。
| 表 1 随机抽取负荷数据的检测结果 |
由表 1可以看出,所提出的智能辨识模型对坏数据的平均检测正确率为89.2%,远远高于采用单一BP神经网络辨识模型的检测正确率,可以看出其令人满意的效果。本文提出的坏数据辨识模型采用WKFCM聚类算法对负荷数据进行聚类得到5条特征曲线,并采用超圆神经元网络坏数据进行辨识,完成对样本的最优或次优划分,提高了坏数据辨识精度。
5 结论本文基于数据挖掘思想对电力负荷历史数据中的坏数据进行辨识和修正,得出以下结论:
1) 提出了基于加权核函数模糊C均值聚类算法(WKFCM),采用核诱导距离代替了复杂的欧氏距离,在目标函数中加入动态权值,为数据集中不同的类分配不同的权值,改善了聚类的效果;
2) 在WKFCM聚类基础上,结合超圆神经网络构成坏数据辨识组合模型,并利用修正公式对检测出的坏数据进行修正,最后实例验证了本文提出的方法的有效性。
| [1] |
张国江, 邱家驹, 李继红.
基于人工神经网络的电力负荷坏数据辨识与调整[J]. 中国电机工程学报, 2001, 21(8): 104–107, 113.
ZHANG Guojiang, QIU Jiaju, LI Jihong. Outlier identification and justification based on neural network[J]. Proceedings of the CSEE, 2001, 21(8): 104–107, 113. (in Chinese) |
| [2] |
莫维仁, 张伯明, 孙宏斌, 等.
扩展短期负荷预测方法的应用[J]. 电网技术, 2003, 27(5): 6–9.
MO Weiren, ZHANG Boming, SUN Hongbing, et al. Application of extended short-term load forecasting[J]. Power System Technology, 2003, 27(5): 6–9. (in Chinese) |
| [3] |
康重庆, 夏清, 相年德.
灰色系统参数估计与不良数据辨识[J]. 清华大学学报:自然科学版, 1997, 37(4): 72–75.
KANG Chongqing, XIA Qing, XIANG Niande. Parameter estimation and bad data identification of gray systems[J]. Journal of Tsinghua University:Science & Technology, 1997, 37(4): 72–75. (in Chinese) |
| [4] | 袁曾任. 人工神经元网络及其应用[M]. 北京: 清华大学出版社, 1999. |
| [5] | Park D C, El-Sharkawi M A, Marks R J Ⅱ, et al. Electric load forecasting using an artificial neural network[J]. IEEE Transactions on Power Systems, 1991, 6(2): 442–449. DOI:10.1109/59.76685 |
| [6] | Drezga I, Rahman S. Input variable selection for ann-based short-term load forecasting[J]. IEEE Transactions on Power Systems, 1998, 13(4): 1238–1244. DOI:10.1109/59.736244 |
| [7] |
李培强, 李欣然, 唐外文, 等.
模糊C均值聚类在电力负荷建模中的应用研究[J]. 湖南大学学报, 2006, 33(3): 41–45.
LI Peiqian, LI Xinran, TANG Waiwen, et al. Fuzzy C means clustering based static electric load modeling[J]. Journal of Hunan University, 2006, 33(3): 41–45. (in Chinese) |
| [8] | Huang S J, Shih K R. Short-term load forecasting via ARMA model identification including non-Gaussian process considerations[J]. IEEE Transactions on Power Systems, 2003, 18(2): 673–679. DOI:10.1109/TPWRS.2003.811010 |
| [9] | 李相镐, 李洪兴, 陈世权. 模糊聚类分析及其应用[M]. 贵州: 贵州科技出版社, 1994. |
| [10] |
张晓星, 程其云, 周湶, 等.
基于数据挖掘的电力负荷脏数据动态智能清洗[J]. 电力系统自动化, 2005, 29(8): 60–64.
ZHANG Xiaoxing, CHENG Qiyun, ZHOU Quan, et al. Dynamic intelligent cleaning for dirty electric load data based on data mining[J]. Automatic of Electrical Power Systems, 2005, 29(8): 60–64. (in Chinese) |
| [11] |
高翠芳, 吴小俊.
一种改进的加权模糊核聚类算法[J]. 数据采集与处理, 2010, 25(5): 631–636.
GAO Cuifang, WU Xiaojun. Improved algorithm for weighted fuzzy kernel clustering analysis[J]. Journal of Data Acquisition & Processing, 2010, 25(5): 631–636. (in Chinese) |
| [12] | Sato-Ilic M. Fuzzy regression analysis using fuzzy clustering[C]//Proceedings of the 2002 Annual Meeting of the North American Fuzzy Information Processing Society (NAFIPS), June 27-29, New Orleans, LA, USA. Piscataway:IEEE Press, 2002, 2002:57-62. |
| [13] |
柳炳祥, 李海林, 李慧颖.
基于模糊模式识别的超圆神经网络模型[J]. 微计算机信息, 2007, 23(5): 303–304, 308.
LIU Bingxiang, LI Hailin, LI Huiying. Research of the algorithm of artificial neural network based on fuzzy pattern recognition[J]. Control & Automation, 2007, 23(5): 303–304, 308. (in Chinese) |
| [14] | Abu-El-Magd M A, Findlay R D. A new approach using artificial neural network and time series models for short term load forecasting[C]//Proceedings of the 2003 IEEE Canadian Conference on Electrical and Computer Engineering, May 4-7, 2003, Montreal, Canada. Piscataway:IEEE Press, 2003, 3:1723-1726. |
| [15] | Taylor J W, Buizza R. Neural network load forecasting with weather ensemble predictions[J]. IEEE Transactions on Power Systems, 2002, 17(3): 626–632. DOI:10.1109/TPWRS.2002.800906 |
| [16] | Marin F J, Garcia-Lagos F, Joya G, et al. Global model for short-term load forecasting using artificial neural networks[J]. IEE Proceedings of Generatio, Transmission and Distribution, 2002, 149(2): 121–125. DOI:10.1049/ip-gtd:20020224 |
| [17] | Senjyu T, Takara H, Uezato K, et al. One-hour-ahead load forecasting using neural network[J]. IEEE Transactions on Power Systems, 2002, 17(1): 113–118. DOI:10.1109/59.982201 |
| [18] | Ling S H, Leung F H F, Lam H K, et al. Short-term electric load forecasting based on a neural fuzzy network[J]. IEEE Transactions on Industrial Electronics, 2003, 50(6): 1305–1316. DOI:10.1109/TIE.2003.819572 |
 2013, Vol. 36
2013, Vol. 36

