2. 重庆市万州供电局, 重庆 400000
2. Chongqing Wanzhou Power Supply Bureau, Chongqing 400000, China
由于混合动力汽车融合了传统内燃机汽车和电动汽车的优点,其已被世界汽车工业确立为中长期内清洁化汽车的主要发展方向[1-2]。并联混合动力汽车(PHEV)作为混合动力汽车中一种具有发展前景的结构形式[3],其控制策略成为目前的研究热点[4]。PHEV控制策略的基本功能是在满足整车动力需求的前提下,实现发动机、电动机之间合理的转矩分配,获得最优燃油消耗率、最小尾气排放以及维持电池荷电状态稳定,因而整车性能与采用的整车控制策略密切相关[5]。而现有控制策略主要有基于稳态优化的控制策略[6]、基于动态优化的控制策略[7]和基于模糊逻辑的控制策略[8]。由于模糊控制策略的鲁棒性强,实时性好并且控制简单,能够克服其他控制策略的不足之处[9],因此很适合与多目标最优化算法结合后作为PHEV整车控制策略。
提出的模糊多目标控制策略以整车燃油消耗率和尾气排放为目标,兼顾维持电池荷电状态稳定,应用最小加权偏差法对模糊化后的可选工作点进行寻优计算,求得最优工作点作为输出。同时在寻优过程中使用部分未知偏好加权方法来满足不同工况对优化目标的偏好差异,也即不同地域环境(例如:市区与郊区)对尾气排放限制的差异。
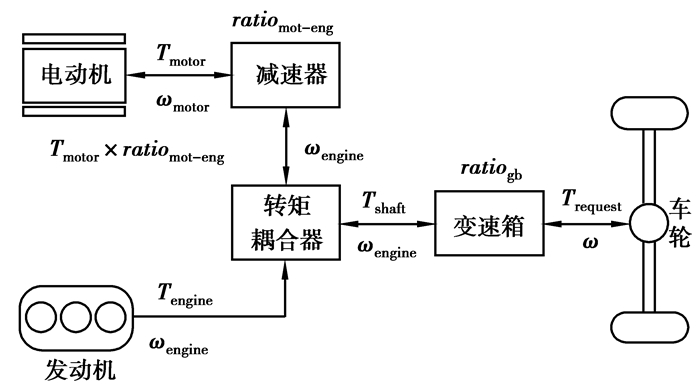
1 PHEV动力总成分析图 1为本文研究的并联混合动力汽车动力总成构型,其采用转矩耦合式的并联结构。
|
图 1 PHEV动力总成构型 |
发动机与电动机之间转速和转矩的关系如下
| $ \omega = {\omega _{{\rm{engine}}}} \times rati{o_{{\rm{gb}}}} = \left( {{\omega _{{\rm{motor}}}} \times rati{o_{{\rm{mot - eng}}}}} \right) \times rati{o_{{\rm{gb}}}}, $ | (1) |
| $ \frac{{{T_{{\rm{request}}}}}}{{rati{o_{{\rm{gb}}}}}} = {T_{shaft}} = {T_{{\rm{engine}}}} + {T_{{\rm{motor}}}} \times rati{o_{{\rm{mot - eng}}}}。$ | (2) |
ωengine,Tengine分别为发动机转速和转矩;ωmotor,Tmotor分别为电动机转速和转矩;ratiogb,ratiomot-eng分别为变速箱和减速器的减速比。根据公式(1),(2)可以确定电动机转矩的可选工作范围,也即可选工作点范围。当ω,ratiogb,Trequest给定时,有
| $ \max \left\{ {{T_{{\rm{motor + }}}}} \right\} = \min \left\{ \begin{array}{l} {T_{{\rm{shaft}}}},\\ \max \left\{ {{T_{{\rm{motor}}}}} \right\},\\ \max \left\{ {{T_{{\rm{battery + }}}}} \right\} \end{array} \right\}, $ | (3) |
| $ \max \left\{ {\left| {{T_{{\rm{motor}} - }}} \right|} \right\} = \min \left\{ \begin{array}{l} 0,\\ max\left\{ {{T_{{\rm{engine}}}}} \right\} - {T_{{\rm{shaft}}}},\\ \max \left\{ {{T_{{\rm{motor}}}}} \right\},\\ \max \left\{ {\left| {{T_{{\rm{battery}} - }}} \right|} \right\} \end{array} \right\}。$ | (4) |
其中,max{Tmotor+},max{|Tmotor-|}分别为电动机正、负转矩的可选最大值,即有-max{|Tmotor-|}≤Tmotor≤max{Tmotor+}。本文此后对最优工作点进行的分析计算都限制在公式(3),(4)所确定的可选工作点范围内。
2 候选工作点燃油消耗与尾气排放为了确定最优工作点,需要计算整车燃油消耗,也即需要计算各个可选工作点的发动机系统燃油消耗和电动机电池系统等效燃油消耗的总和。下面分三步阐述如何计算整车燃油消耗。
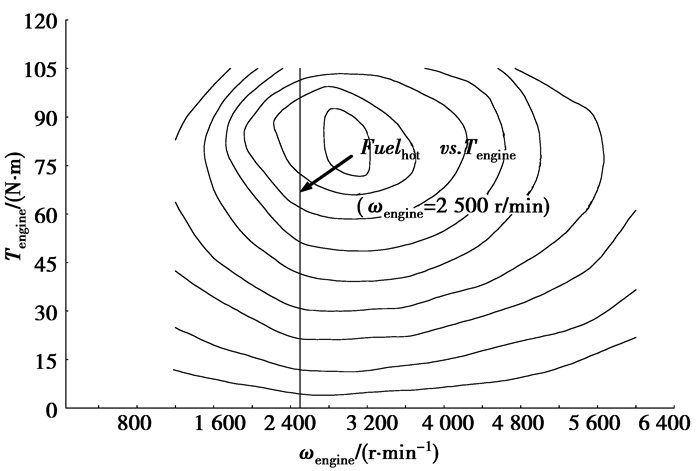
2.1 发动机燃油消耗在给定发动机转速ωengine =2 500 r/min下,根据发动机稳态万有特性图(图 2)可得Fuelhot vs. Tengine。又根据公式(2),进而可得Fuelhot vs. Tmotor。Fuelhot为热发动机燃油消耗。
|
图 2 发动机万有特性图 |
考虑到发动机效率对温度敏感,有必要引入一个温度系数对其效率进行修正。使用式(5)来反映这一现象。
| $ \begin{array}{l} Fue{l_{{\rm{engine}}}} = Fue{l_{{\rm{hot}}}} \times \left( {Coef{f_{{\rm{engine}}}} + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{{\left( {\frac{{95 - Tem{p_{{\rm{engine}}}}}}{{75}}} \right)}^{Ex{p_{{\rm{engine}}}}}}} \right)。\end{array} $ | (5) |
其中,Fuelengine为温度修正后发动机燃油消耗,Tempengine为发动机冷却剂温度,Coeffengine和Expengine为常数。在对Fuelhot vs. Tmotor进行温度修正后即可获得发动机燃油消耗曲线Fuelengine vs. Tmotor(图 3)。

|
图 3 发动机燃油消耗曲线 |
使用一种等效燃油消耗的概念来度量电动机的能量消耗,以避免计算电池系统与其他系统之间复杂的时变非线性能量转换关系。等效燃油消耗是一定量的假设能量,用于平衡由于放电(Tmotor > 0)或者充电(Tmotor < 0)而引起的电池荷电状态变化(ΔSOC)。
2.2.1 制动回收能量当汽车减速时,电机输出负转矩同时对电池进行充电,进而使得电池SOC升高。由于回收这些制动能量时不需要额外消耗其他的能量,所以这些回收能量被视为一种“免费能量”。当选择最优工作点时,以电池SOC改变量(ΔSOCregen)的形式计算这些回收能量。
由于精确预测ΔSOCregen的时间复杂度过高,本文根据最近工作状态来估算未来ΔSOCregen。具体而言,通过重复记录最近时间窗口Tframe的ΔSOCregen,可以获得一组以时间为序的ΔSOCregen, i,即:ΔSOCregen, 1, ΔSOCregen, 2, …, ΔSOCregen, n。对时间上最近的m个求平均值,其结果作为预测值ΔSOCregen。
| $ \frac{{\Delta SO{C_{{\rm{regen}}}} = \sum\limits_{i = 0}^{m - 1} {\Delta SO{C_{{\rm{regen,}}n - i}}} }}{{\left( {m \times {T_{{\rm{frame}}}}} \right)}} $ | (6) |
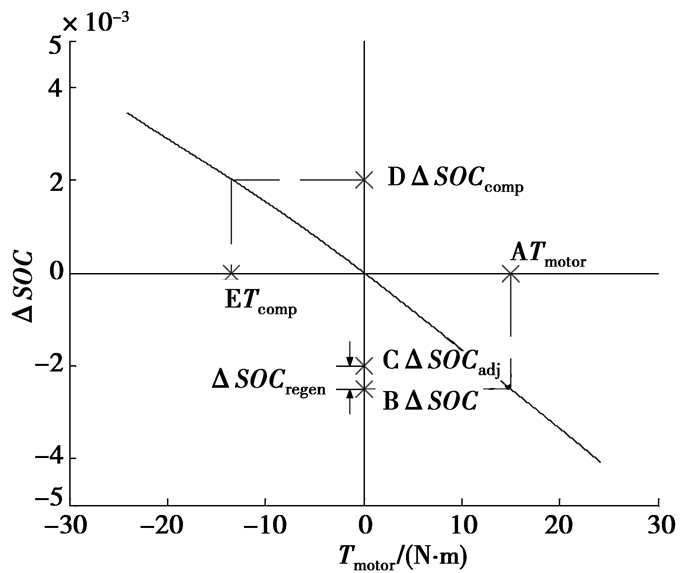
如果不考虑回收制动ΔSOCregen,当Tmotor > 0时,电机将电池储能转化为机械能以驱动传动系统。这会电池放电以提供电机所需的电能,即ΔSOC < 0。同理,当Tmotor > 0时,电池充电,ΔSOC > 0。电机输出转矩Tmotor与其产生的电池能量变化ΔSOC之间的关系如图 4所示。一般而言,ΔSOC与Tmotor不是线性关系。这主要是由于两个原因造成的:1)电机效率与电机转矩不是线性的;2)电池充放电内阻不同且非线性。
|
图 4 电机输出转矩与电池电量变化 |
取可选工作点内任意一点Tmotor,不妨假设其为图 4点A。则根据曲线ΔSOC vs. Tmotor可得对应的电池ΔSOC (图 4点B)。如前所述,这表示定量的Tmotor在一定时间内引起电池荷电状态的变化ΔSOC。再将回收制动能量考虑进来,电池荷电状态会被提升ΔSOCregen (图 4线段BC)。经过修正后的SOC变化量即为ΔSOCadj (图 4点C)。
| $ \Delta SO{C_{{\rm{adj}}}} = \Delta SOC + \Delta SO{C_{{\rm{regen}}}}。$ | (7) |
笔者采用电池充放电平衡策略。即对任意循环工况,虽然行驶过程中SOC会出现升降变化,但是最终SOC都须尽可能趋近于初始SOC。对具体一个循环工况而言,如果在某段时间电池放电一定能量ΔSOCadj以驱动电机,根据充放电平衡策略则电池SOC需在未来某一时间段被补偿充电相同能量ΔSOCcomp (图 4点D),即有
| $ \Delta SO{C_{{\rm{comp}}}} = - 1 \times \Delta SO{C_{{\rm{adj}}}}。$ | (8) |
将ΔSOCcomp代回曲线ΔSOC vs. Tmotor可得Tcomp (图 4点E)。其表示补偿电池荷电状态变化所需要的电机转矩。
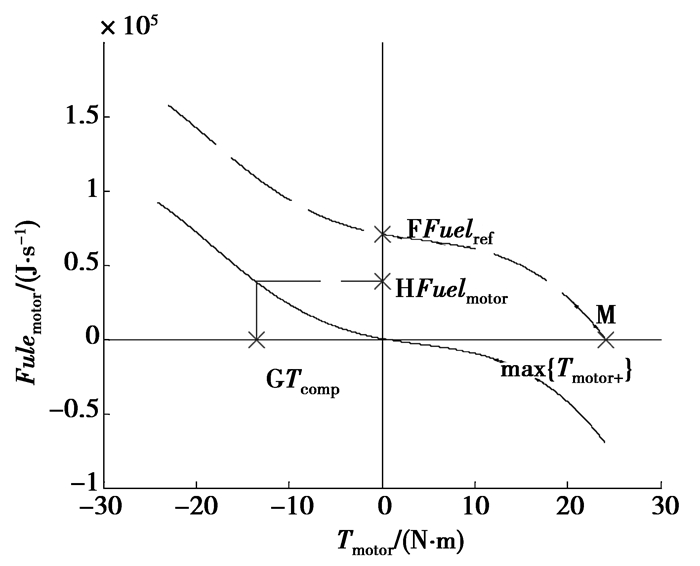
2.2.3 电机输出转矩产生的等效燃油消耗图 5中虚线与图 3中Fuelengine vs. Tmotor相同。而在图 5这一特定工况下,当电机转矩取最大值时(点M),有max{Tmotor+}=Tshaft,即此时电机提供所有Tshaft。于是Tengine=0,即在图 4点M处发动机不工作,无燃油消耗。随着Tmotor减小,发动机负载增加,相应的发动机油耗上升。当Tmotor减小到0,则发动机提供所有的Tshaft,此时的发动机油耗被定义为Fuelref (图 5点F)。即如果电动机常关,相应的发动机油耗必为Fuelref。
|
图 5 补偿转矩与等效燃油消耗 |
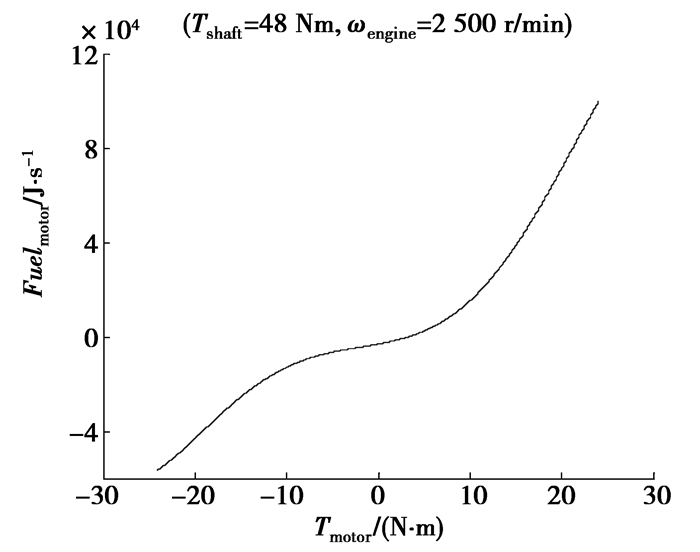
图 5中虚线减去Fuelref后所得的实线即为由于补偿电池荷电状态变化而需要消耗的能量。将前面图 4所得的代Tcomp入图 5中(图 5点G),可得相对应的补偿能量Fuelmotor(图 5点H)。Fuelmotor定义为电机输出转矩为Tmotor时的等效燃油消耗量。逐一计算所有可选工作点,建立图 6中的Fuelmotor vs. Tmotor曲线。
|
图 6 电机输出转矩与等效燃油消耗 |
需要指出上述方法是建立在假设所有当前电机能量消耗都会在未来某一时刻以类似工况条件(Tshaft和ωengine)被补偿。另外,实际计算中Tmotor的范围会适当大于其可选范围,以避免图 5中Tmotor计算时超出范围。这主要是由两个原因造成的:1)max{Tmotor+}和max{Tmotor-}可能不相等;2)ΔSOCadj被回收能量ΔSOCregen抬高。
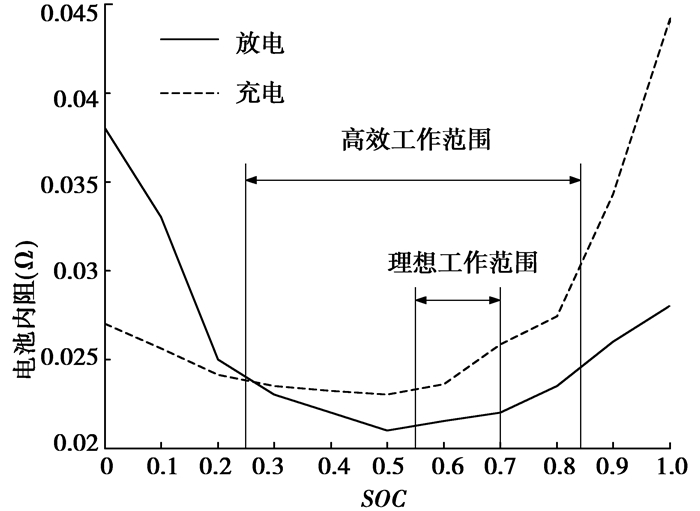
2.2.4 SOC修正系数控制策略在根据工作点效率高低对电动机电池系统进行充放电的同时,必须保证电池SOC被维持在一定范围之内[10]。限制电池SOC的工作范围是因为:1)根据充放电平衡策略,电池理想工作范围必然小于其高效工作范围;2)电池高效工作范围并不完全适用于实际工况。例如根据图 7中高效工作范围,电池SOC可以低至0.25。而此时的SOC在实际工况中显然过低,可能无法满足未来工况的转矩需求。
|
图 7 SOC高效工作范围和理想工作范围 |
因为上述原因,需要通过一个基于SOC的修正系数Scale来控制电机的充放电趋势,以维持电池荷电状态在理想工作范围之内:
| $ Fue{l_{{\rm{mother,scaled}}}} = Fue{l_{{\rm{mother}}}} \times Scale。$ | (9) |
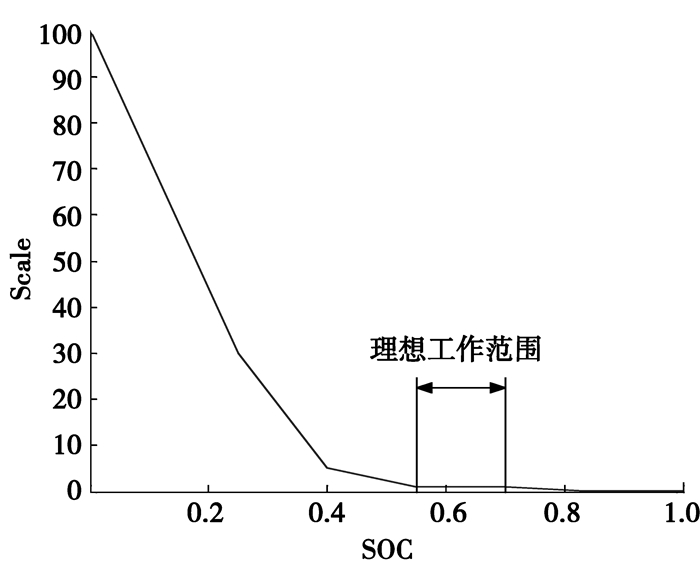
Fuelmotor, scaled即为修正后的电机等效燃油消耗。根据SOC的不同,公式(9)中Scale被分为3个部分(图 8):当SOC位于理想工作范围内,Scale趋近于1,即此工况下无需额外调整SOC;当SOC低于理想工作范围,Scale增大使得消耗电池能量变得不经济,而对电池充电则更经济;当SOC高于理想工作范围,类似地Scale减小使得放电行为比充电行为更为经济。
|
图 8 SOC调整系数 |
将前面得到的发动机燃油消耗与电动机等效燃油消耗叠加得到可选工作范围内的整车燃油消耗
| $ Fue{l_{{\rm{vehicle}}}} = Fue{l_{{\rm{engine}}}} + Fue{l_{{\rm{mother,scaled}}}}。$ | (10) |
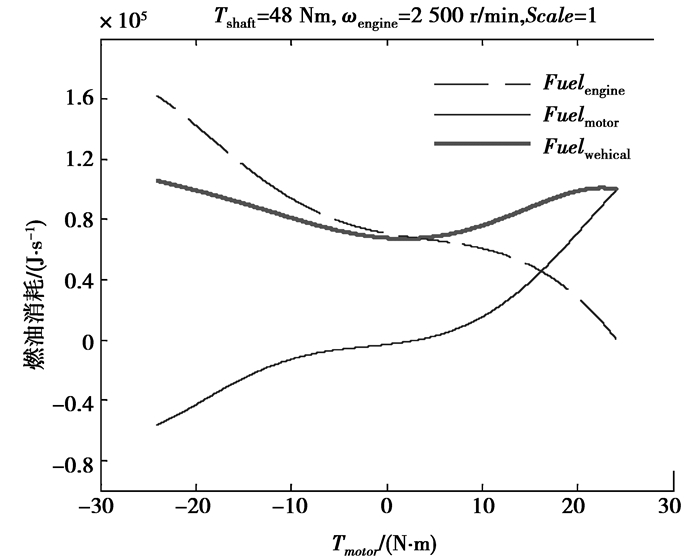
图 9为给定Tshaft和ωengine下可选工作点范围内的的整车燃油消耗。其中Tmotor的可选范围由公式3和4确定。
|
图 9 整车燃油消耗 |
计算发动机尾气排放与计算发动机燃油消耗过程类似。首先,根据发动机排放特性图(图 10)确定给定转速下四种主要排放物(HC, CO, NOX, PM)与发动机转矩Tengine的关系。

|
图 10 发动机尾气排放图(CO) |
与燃油消耗类似,当发动机温度升高,其尾气排放呈下降趋势。所以,需要对尾气排放进行温度修正。以CO为例,其温度修正公式如下
| $ C{O_{{\rm{cold}}}} = C{O_{{\rm{hot}}}} \times \left( {Coef{f_{CO}} + {{\left( {\frac{{95 - Tem{p_{engine}}}}{{75}}} \right)}^{Ex{p_{CO}}}}} \right)。$ | (11) |
其中,COhot为热发动机尾气排放,COcold为温度修正后发动机尾气排放,ExpCO和CoeffCO为常数。最后,需要计算尾气催化剂的转化效率,其转化效率为催化剂温度的函数EffCO(Tcatalyst)。经过催化剂净化后的即可得到排气管尾气排放CO
| $ CO = C{O_{{\rm{cold}}}} \times \left( {1 - Ef{f_{CO}}\left( {{T_{{\rm{catalyst}}}}} \right)} \right)。$ | (12) |
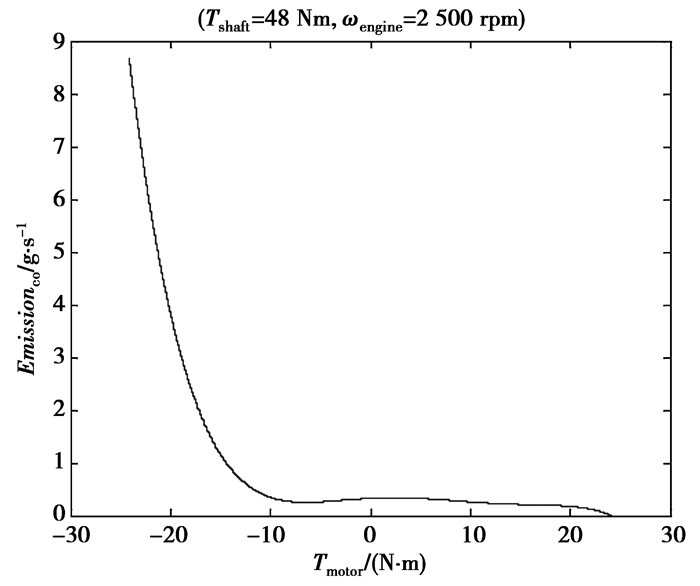
给定工况下,可选工作点范围内的整车尾气排放(CO)与电动机转矩Tmotor的关系如图 11所示。
|
图 11 整车尾气排放(CO) vs. Tmotor |
为了计算最优工作点,根据上述计算结果建立多目标最优化问题如下
| $ \begin{array}{*{20}{c}} {\min \left\{ {\begin{array}{*{20}{c}} {Fue{l_{{\rm{vehicle}}}}\left( {{T_{{\rm{motor}}}}} \right),}\\ {HC\left( {{T_{{\rm{motor}}}}} \right),}\\ {CO\left( {{T_{{\rm{motor}}}}} \right),}\\ {N{O_X}\left( {{T_{{\rm{motor}}}}} \right),}\\ {PM\left( {{T_{{\rm{motor}}}}} \right)} \end{array}} \right\},}\\ {{\rm{s}}{\rm{.}}\;{\rm{t}}{\rm{.}}\;\;\;\; - {\rm{max}}\left\{ {\left| {{T_{{\rm{motor}} - }}} \right|} \right\} \le {T_{{\rm{motor}}}} \le {\rm{max}}\left\{ {{T_{{\rm{motor}} + }}} \right\}。} \end{array} $ | (13) |
为表述方便,用如下标准化公式表示式(13)
| $ \left. \begin{array}{l} \min \left( {{f_1}\left( x \right),{f_2}\left( x \right), \cdots ,{f_m}\left( x \right)} \right),\\ {\rm{s}}{\rm{.}}\;{\rm{t}}{\rm{.}}\;\;x \in X = \left\{ {{x_1},{x_2}, \cdots ,{x_n}} \right\}。\end{array} \right\} $ | (14) |
其中,fi(x) (i=1, …, m)是优化目标;X={x1, x2, …, xn}是可选方案集。本文采用最小加权偏差方法对公式(14)进行寻优求解。
3.1 模糊化过程定义fi*为优化目标fi(x), i=1, …, m的理想目标值,其具体值定义在表 1中。
| 表 1 燃油消耗和尾气排放理想目标值 |
根据定义,控制策略需要使各目标尽可能地靠近理想目标值。Zimmerman等人的研究[11]证明应用模糊集可以有效求解此问题。本文使用的三角形隶属度函数定义如下:
| $ {\mu _{ij}} = {\mu _{{f_i}}}\left( {{x_j}} \right) = \left\{ \begin{array}{l} 1\;\;\;\;{f_i}\left( {{x_j}} \right) \le f_i^ * ;\\ \frac{{f_i^{\max } - {f_i}\left( {{x_j}} \right)}}{{f_i^{\max } - f_i^ * }},f_i^ * \le {f_i}\left( {{x_j}} \right) \le f_i^{\max }\\ 1 \le i \le m\\ 0,{f_i}\left( {{x_j}} \right) \ge f_i^{\max };1 \le j \le n。\end{array} \right. $ | (15) |
其中fimax是优化目标的容忍上限。由于多目标优化问题中各目标的容忍上限不易确定,使用理想方案支付表[12](表 2)计算fimax的具体值。
| 表 2 理想方案支付表 |
理想方案x+的目标值可以定义为(f1(x1*), f2(x2*), …, fm(xm*)),即所有目标分量fi(x)都分别取得最小值时所得方案。理想方案x+不必是可行方案,即x+∉X。其中
| $ {f_i}\left( {{x^{i * }}} \right) = \mathop {\min }\limits_{x \in X} {f_i}\left( X \right),\;\;\;\;i = 1, \cdots ,m。$ | (16) |
显然,fi(xi*)为表 2中对角线元素。根据每行所得的xi*求得此行其余m-1个元素,即
| $ {f_{ik}} = {f_i}\left( {{x^{k * }}} \right),\;\;\;i,k = 1, \cdots ,m。$ | (17) |
根据求得的支付表,定义各目标容忍上限fimax
| $ f_i^{\max } = \mathop {\max }\limits_{k = 1, \cdots ,m} {f_{ik}},\;\;\;i = 1, \cdots ,m。$ | (18) |
由于整车控制实时性的限制,本文中多目标优化是通过建立评价函数将多目标问题转换为单目标问题进行求解的。而评价函数的建立是基于决策者对各目标的优先偏好,即是说各目标偏好加权需要被预先确定。由于混合动力系统是非线性时变系统,所以难以确定所有偏好加权。于是偏好加权被定义为部分未知,而其未知部分使用最小加权偏差法确定。
为了不失一般性,不妨假设偏好加权的前p(p≥ 1)个为未知,而其后m-p个为已知
| $ \left. \begin{array}{l} \omega = \left( {{\omega _1},{\omega _2}, \cdots ,{\omega _m}} \right) = \left( {{\omega ^0},{\omega ^ * }} \right),\\ {\omega ^0} = \left( {\omega _1^0,\omega _2^0, \cdots ,\omega _p^0} \right),\\ {\omega ^ * } = \left( {\omega _{p + 1}^ * ,\omega _{p + 2}^ * , \cdots ,\omega _m^ * } \right)。\end{array} \right\} $ | (19) |
其中,ωi0(i=1, 2, …, p)是未知,ωi*(i=p+1, p+2, …, m)是已知。
理想方案x+的隶属度定义如下
| $ A = {\left( {{\alpha _1},{\alpha _2}, \cdots ,{\alpha _m}} \right)^{\rm{T}}}, $ | (20) |
| $ {\alpha _i} = \mathop {\max }\limits_{1 \le j \le n} {\mu _{ij}},\;\;\;i = 1,2, \cdots ,m。$ | (21) |
显然,理想方案x+的隶属度是所有可选方案(x∈{x1, x2, …, xn})中的最大值。定义如下目标函数
| $ {g_j}\left( {{\omega ^0}} \right) = \sum\limits_{i = 1}^m {{\omega _i}\left( {{\alpha _i} - {\mu _{ij}}} \right)} ,\;\;\;\;j = 1,2, \cdots ,n。$ | (22) |
其表示可选方案xj各目标相对理想方案x+的加权偏差距离之和。对于给定的偏好加权向量ω,若gj(ω0)越小,则xj越靠近理想方案,也即xj越优。于是,建立多目标决策模型
| $ \begin{array}{*{20}{c}} {\min \left\{ {g\left( {{\omega ^0}} \right) = \left( {{g_1}\left( {{\omega ^0}} \right),{g_2}\left( {{\omega ^0}} \right), \cdots ,{g_n}\left( {{\omega ^0}} \right)} \right)} \right\},}\\ {{\rm{s}}{\rm{.}}\;{\rm{t}}{\rm{.}}\;\;\;\left\{ \begin{array}{l} \sum\limits_{i = 1}^p {{{\left( {\omega _i^0} \right)}^2}} = c,\\ \omega _i^0 \ge 0,\;\;\;\;i = 1,2, \cdots ,p。\end{array} \right.} \end{array} $ | (23) |
考虑到gj(ω)之间没有优先性,公式(23)的多目标决策模型可以转换为如下等效单目标决策模型
| $ \begin{array}{*{20}{c}} {\min \left\{ {\sum\limits_{j = 1}^n {{g_j}\left( {{\omega ^0}} \right)} } \right\},}\\ {{\rm{s}}{\rm{.}}\;{\rm{t}}{\rm{.}}\;\;\;\left\{ \begin{array}{l} \sum\limits_{i = 1}^p {{{\left( {\omega _i^0} \right)}^2}} = c,\\ \omega _i^0 \ge 0,\;\;\;\;i = 1,2, \cdots ,p。\end{array} \right.} \end{array} $ | (24) |
运用拉格朗日乘数法求解公式(23)中的非线性规划问题。首先,建立相应拉格朗日函数
| $ \begin{array}{*{20}{c}} {L\left( {{\omega ^0},\lambda } \right) = \sum\limits_{j = 1}^n {{g_j}\left( {{\omega ^0}} \right)} + \lambda \left( {\sum\limits_{i = 1}^p {{{\left( {\omega _i^0} \right)}^2} - c} } \right) = }\\ {\sum\limits_{j = 1}^n {\sum\limits_{i = 1}^m {{\omega _i}\left( {{\alpha _i} - {\mu _{ij}}} \right)} } + \lambda \left( {\sum\limits_{i = 1}^p {{{\left( {\omega _i^0} \right)}^2} - c} } \right)。} \end{array} $ | (25) |
其中,λ是拉格朗日乘子。然后,分别对拉格朗日函数L(ω0, λ)求ωi00 (i=1, 2, …, p)和λ的偏导并令其为0。
| $ \begin{array}{*{20}{c}} {\frac{{\partial L\left( {{\omega ^0},\lambda } \right)}}{{\partial \omega _i^0}} = \sum\limits_{j = 1}^n {\left( {{\alpha _i} - {\mu _{ij}}} \right) + 2\lambda \omega _i^0} = 0,\;\;\;\;i = 1,2, \cdots ,p,}\\ {\frac{{\partial L\left( {{\omega ^0},\lambda } \right)}}{{\partial \lambda }} = \sum\limits_{i = 1}^p {{{\left( {\omega _i^0} \right)}^2} - c = 0} 。} \end{array} $ | (26) |
求解此方程组,可得偏好权重
| $ \begin{array}{*{20}{c}} {\omega _i^0 = \sum\limits_{j = 1}^n {\left( {{\alpha _i} - {\mu _{ij}}} \right)} \sqrt {\frac{c}{{\sum\limits_{i = 1}^p {{{\left[ {\sum\limits_{j = 1}^n {\left( {{\alpha _i} - {\mu _{ij}}} \right)} } \right]}^2}} }}} ,}\\ {i = 1,2, \cdots ,p。} \end{array} $ | (27) |
接着,对求得的偏好权重进行标准化
| $ \bar \omega _i^0 = \frac{{\left( {1 - \sum\limits_{i = p + 1}^m {\omega _i^ * } } \right)\sum\limits_{j = 1}^n {\left( {{\alpha _i} - {\mu _{ij}}} \right)} }}{{\sum\limits_{i = 1}^p {\sum\limits_{j = 1}^n {\left( {{\alpha _i} - {\mu _{ij}}} \right)} } }},\;\;\;\;i = 1,2, \cdots ,p。$ | (28) |
联合偏好权重已知部分可得最小偏差权重
| $ \begin{array}{*{20}{c}} {{\omega ^{MD}} = \left\{ {\omega _1^{MD},\omega _2^{MD}, \cdots ,\omega _m^{MD}} \right\} = }\\ {\left\{ {{{\bar \omega }^0},{\omega ^ * }} \right\} = \left\{ {\bar \omega _1^0,\bar \omega _2^0, \cdots ,\bar \omega _p^0,\omega _{p + 1}^ * ,\omega _{p + 2}^ * , \cdots ,\omega _m^ * } \right\}。} \end{array} $ | (29) |
联立公式(20), (28), (29)即可求得可选集X中各可选方案xj的加权偏差值。根据加权偏差值大小就可以确定各个方案的优劣关系,进而选定最优可选方案xopt
| $ \begin{array}{*{20}{c}} {{g_{{\rm{opt}}}}\left( {{\omega ^{MD}}} \right) = \sum\limits_{i = 1}^m {\omega _i^{MD}{\mu _{{f_i}}}\left( {{x_{{\rm{opt}}}}} \right)} = \min \left\{ {\sum\limits_{i = 1}^m {\omega _i^{MD}{\mu _{{f_i}}}\left( {{x_j}} \right)} ,} \right.}\\ {\left. {j = 1,2, \cdots ,n} \right\}。} \end{array} $ | (30) |
最小加权偏差法能够保证在不同工况下控制策略的灵活性。具体而言,在郊区或高速公路,控制策略将优先考虑燃油消耗;而在市区或其它排放限制区域,尾气排放和燃油消耗将具有同等的优先级。此问题在最小加权偏差法中的处理方法如下:
1) 在非排放限制工况中,各排放目标的权重定义为未知,而燃油消耗目标的权重ωfuel定义为常量(本文中,ωfuel=0.6)。这保证了燃油消耗总是获得最高优先级。
2) 在排放限制工况中,所有目标权重皆为未知,即p=m。这意味着确定最小加权偏差值时,各目标间优先级相同。而此时的最小加权偏差法可定义为
| $ \begin{array}{*{20}{c}} {\bar \omega _i^0 = \frac{{\sum\limits_{j = 1}^n {\left( {{\alpha _i} - {\mu _{ij}}} \right)} }}{{\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {\left( {{\alpha _i} - {\mu _{ij}}} \right)} } }},\;\;\;\;i = 1,2, \cdots ,m.}\\ {{\omega ^{MD}} = \left\{ {\omega _1^0,\omega _2^0, \cdots ,\omega _m^0} \right\}。} \end{array} $ | (31) |
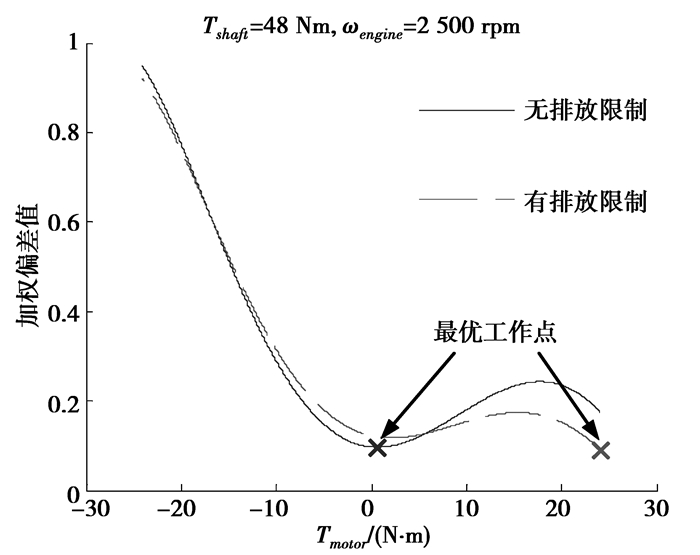
根据式(30),计算具体工况中各可选工作点的加权偏差值,可得具有最小加权偏差值的最优工作点(图 12)。显然,在有排放限制下最优工作点的电动机转矩Tmotor更大。这表明此时控制策略更倾向于使用无尾气排放的电能。
|
图 12 加权偏差值 |
使用ADVISOR在MATLAB/SIMULINK环境中对前述模糊控制策略(FMCS)进行仿真验证,并使用基于规则集的传统阈值控制策略(RBCS)[13-15]进行性能对比测试。通过两种控制策略的仿真对比,可以证明模糊多目标控制策略的性能提升。
仿真验证中使用的PHEV系统参数如下:电喷汽油发动机,排量1.4 L,额定功率50 kW;交流异步电动机,额定功率20 kW,峰值功率40 kW;锂电池组,额定电压300 V DC,额定容量10Ah;5档手动变速箱;整车质量1 050 kg。
4.1 NEDC工况工作效率对比选用新欧洲循环工况(NEDC)进行仿真分析是因为NEDC同时包括了市区工况(0~800 s,有排放限制)和郊区工况(801~1 185 s,无排放限制)。
图 13是NEDC工况下FMCS与RBCS转矩分配的仿真对比。FMCS的Tengine比RBCS的更一致,并且在市区工况中RBCS的Tengine主要处于低转矩区域。这表明RBCS的发动机在低速工况下工作在低效率区域。此外,比较FMCS分别位于有限制排放和无限制排放下的Tmotor,可知在有排放限制时FMCS更倾向于使用电动机。最后,由于FMCS采用充放电平衡策略,所以FMCS的最终SOC(0.651)比RBCS的(0.601)更接近初始SOC(0.7)。

|
图 13 FMCS和RBCS在NEDC工况下对比仿真 |
图 14是两种控制策略的发动机工作点在万有特性图上的分布。FMCS的发动机工作点相比RBCS更多地集中在高效区,同时在低速区RBCS的发动机工作点散布在效率不高的低负荷区。这说明FMCS能够控制发动机更高效地工作,进而减少燃油消耗。

|
图 14 FMCS和RBCS发动机工作点在效率图上的分布 |
PHEV最要部件在NEDC工况下的平均效率如表 3所示。由于电动机电池系统自身的高效区分别较宽并且对负载不敏感,所以电动机和电池的效率在FMCS与RBCS之间差异不如发动机的明显。
| 表 3 在NEDC工况下主要部件效率 |
为了准确比较FMCS和RBCS的燃油消耗,电池SOC在循环工况的起始点和结束点都必须保证相同。因此,在相同循环工况下两种控制策略的初始SOC从0.7到0.35进行一系列仿真测试。根据仿真结果使用线性回归求得燃油消耗与SOC改变量之间的关系。进而可以得到起始点与结束点SOC无改变情况下的燃油消耗[16]。根据上述算法,本文选用了表 4中4种典型循环工况进行FMCS与RBCS之间燃油消耗和尾气排放的对比测试。
| 表 4 循环工况及其排放限制 |
| 表 5 燃油消耗以及尾气排放对比 |

|
图 15 四种工况中FMCS对RBCS的改善比例 |
1) 比较不同循环工况下的发动机燃油消耗,FMCS(方差值:0.853)的燃油消耗比RBCS(方差值:0.148 6)的更一致。
2) 在兼有市区和郊区工况的循环工况(NEDC,1015)中,FMCS燃油消耗的改善更明显。而在高速公路循环工况(HWFET)中,由于工况本身使得发动机工作效率高于城市工况,所以FMCS的改善有限。
3) 在纯城市循环工况(UDDS)中,FMCS可以极大改善尾气排放水平。另外,在高速公路(HWFET)上FMCS的尾气排放较RBCS仍有明显改善。
4 结论通过等效燃油消耗的概念,FMCS将整车燃油消耗和尾气排放作为优化目标,控制整车转矩分配同时保证电池荷电状态稳定。考虑到不同工况对目标偏好的不同,使用了最小加权偏差法进行多目标求解。仿真结果证明FMCS在燃油消耗与尾气排放之间进行的折中选择可以有效维持电池荷电状态,并且充分满足用户动力需求。但是由于FMCS使用充放电平衡策略使得其不适用于插电式PHEV中,所以后续研究将引入全局优化算法来保证控制策略的通用性。
| [1] | Xin L, Williamson S S. Assessment of efficiency improvement techniques for future power electronics intensive hybrid electric vehicle drive trains[C]//Proceedings of the 2007 IEEE Canada Electrical Power Conference, October 25-26, 2007, Montreal, Que., Canada. Piscataway:IEEE Press, 2007:268-273. |
| [2] | Bayindir K C, Gözüküçük M A, Teke A. A comprehensive overview of hybrid electric vehicle:powertrain configurations, powertrain control techniques and electronic control units[J]. Energy Conversion and Management, 2011, 52(2): 1305–1313. DOI:10.1016/j.enconman.2010.09.028 |
| [3] | Chan C C. The state of the art of electric, hybrid, and fuel cell vehicles[J]. Proceedings of the IEEE, 2007, 95(4): 704–718. DOI:10.1109/JPROC.2007.892489 |
| [4] | Salmasi F R. Control strategies for hybrid electric vehicles:evolution, classification, comparison, and future trends[J]. IEEE Transactions on Vehicular Technology, 2007, 56(5): 2393–2404. DOI:10.1109/TVT.2007.899933 |
| [5] | Williamson S S, Emadi A. Comparative assessment of hybrid electric and fuel cell vehicles based on comprehensive well-to-wheels efficiency analysis[J]. IEEE Transactions on Vehicular Technology, 2005, 54(3): 856–862. DOI:10.1109/TVT.2005.847444 |
| [6] |
王锋, 冒晓建, 卓斌. ISG并联混合动力轿车最优转矩分配策略[J].重庆大学学报, 2008, 31(5):499-504. WANG Feng, MAO Xiaojian. Torque distribution for an integrated starter generator parallel hybrid electric car[J]. Journal of Chongqing University, 2008, 31(5):499-504. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=five200805007&dbname=CJFD&dbcode=CJFQ |
| [7] |
朱道伟, 谢晖, 严英, 等.
基于道路工况自学习的混合动力城市客车控制策略动态优化[J]. 机械工程学报, 2010, 46(6): 33–38.
ZHU Daowei, XIE Hui, YAN Ying, et al. Control strategy dynamic optimization of the hybrid electric bus based on driving cycle self-learning[J]. Chinese Journal of Mechanical Engineering, 2010, 46(6): 33–38. (in Chinese) |
| [8] | Kheir N A, Salman M A, SchoutenN J. Emissions and fuel economy trade-off for hybrid vehicles using fuzzy logic[J]. Mathematics and Computer in Simulation, 2004, 66(2/3): 155–172. |
| [9] | Baumann B M, Washington G, Glenn B C, et al. Mechatronic design and control of hybrid electric vehicles[J]. IEEE/ASME Transactions on Mechatronics, 2000, 5(1): 58–72. DOI:10.1109/3516.828590 |
| [10] | Ehsani M, Gao Y M, Butler K L. Application of electrically peaking hybrid (ELPH) propulsion system to a full-size passenger car with simulated design verification[J]. IEEE Transactions on Vehicular Technology, 1999, 48(6): 1779–1787. DOI:10.1109/25.806770 |
| [11] | Zimmermann H J. Fuzzy programming and linear programming with several objective functions[J]. Fuzzy Sets and Systems, 1978, 1(1): 45–55. DOI:10.1016/0165-0114(78)90031-3 |
| [12] | Li S Y, Hu C F. Two-step interactive satisfactory method for fuzzy multiple objective optimization with preemptive priorities[J]. IEEE Transactions on Fuzzy Systems, 2007, 15(3): 417–425. DOI:10.1109/TFUZZ.2006.887463 |
| [13] | Banvait H, Anwar S, Chen Y B. A rule-based energy management strategy for plug-in hybrid electric vehicle(PHEV)[C]//Proceedings of the 2009 Conference on American Control, June 10-12, 2009, St. Louis, MO. Piscataway:IEEE Press, 2009:3938-3943. |
| [14] | Sun H, Yang L F, Jing J Q, et al. Control strategy of hydraulic/electric synergy system in heavy hybrid vehicles[J]. Energy Conversion and Management, 2011, 52(1): 668–674. DOI:10.1016/j.enconman.2010.07.045 |
| [15] | Pisu P, Rizzoni G. A comparative study of supervisory control strategies for hybrid electric vehicles[J]. IEEE Transactions on Control Systems Technology, 2007, 15(3): 506–518. DOI:10.1109/TCST.2007.894649 |
| [16] |
戴一凡, 罗禹贡, 边明远, 等.
一种新型强混合动力结构的控制策略[J]. 汽车工程, 2009(10): 919–923, 951.
DAI Yifan, LUO Yugong, BIAN Mingyuan, et al. The control strategy for a new full hybrid powertrain structure[J]. Automotive Engineering, 2009(10): 919–923, 951. DOI:10.3321/j.issn:1000-680X.2009.10.005 (in Chinese) |
 2013, Vol. 36
2013, Vol. 36


