b. 华中科技大学 控制结构湖北省重点实验室, 湖北 武汉 430074
b. Hubei Key Laboratory of Control Structure, Huazhong University of Science & Technology, Wuhan 430074, Hubei China
流体流动现象广泛存在于自然界和各种工程领域中,所有这些过程都要受质量守恒、动量守恒、能量守恒等基本物理定律的支配,即要满足一定的控制微分方程[1]。计算流体动力学(computational fluid dynamics, CFD)是通过计算机数值计算和图像显示,对包含有流体流动和热传导等相关物理现象的系统所做的分析。CFD的基本思想可以归结为:把原来空间域和时间域上连续的物理场,比如压力场和速度场,用一系列有限个离散点上的变量值的集合来代替,通过一定的原则和方式建立起关于这些离散点上场变量之间关系的代数方程组,然后求解代数方程组获得场变量的近似值[2-3],也就是说CFD的首要问题就是要将这些控制流体流动的微分方程离散化,即把求解区域划分成便于求解的网格模型。传统的CFD离散方法包括有限差分法、有限元法和有限体积法,其中又以有限体积法应用最为广泛[4]。它们都有着各自划分网格的方法,统称为网格生成技术。传统的离散方法都是将求解域划分成均匀的网格,然而在实际应用中,经常出现网格的大变形、某些物理量在很小的区域内却发生了很大的变化,比如流固耦合边界、层流及紊流中的剪切层、爆炸等问题,对于这些问题如果采用简单的均匀网格求解则难以达到合理的精度,因此生成与问题相匹配的计算网格显得尤为重要。文中将移动网格这一数学方法引入CFD计算仿真,在不额外增加计算机资源消耗的前提下,很好地解决了这一类问题。
1 流体动力学控制方程及其解法 1.1 流体动力学控制微分方程任何流动问题都必须满足质量守恒定律。该定律可以描述为:单位时间内流体微元体中质量的增加,等于同一时间内流入该微元体的净质量。按照这一定律,可得质量守恒方程
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \left( {\rho u} \right)}}{{\partial x}} + \frac{{\partial \left( {\rho v} \right)}}{{\partial y}} + \frac{{\partial \left( {\rho w} \right)}}{{\partial z}} = 0, $ | (1) |
式中:ρ为流体密度;u、v、w为速度矢量在x、y、z 3个方向的分量;t为时间。
任何流体都应该满足动量守恒定律。该定律可以描述为:微元体中流体的动量对时间的变化率等于外界作用在该微元体上的各种力之和。按照这一定律,可得著名的Navier-Stokes方程
| $ \rho \frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial t}} + \rho \left( {\mathit{\boldsymbol{u}} \cdot \nabla } \right)\mathit{\boldsymbol{u}} = \nabla \left( { - \rho \mathit{\boldsymbol{I}} + \tau } \right) + F, $ | (2) |
式中:u为速度矢量;I为单位矩阵;τ为流体的粘性应力张量; F为流体的体积力。▽为Hamilton算子。
任何流体还应该满足能量守恒定律。该定律可以描述为:微元体能量的增加率等于微元体的净吸热量和外界对微元体的做功之和。按照这一定律,可得能量守恒方程
| $ \frac{{\partial \left( {\rho T} \right)}}{{\partial t}} + \nabla \cdot \left( {\rho \mathit{\boldsymbol{u}}T} \right) = \nabla \cdot \left( {\frac{k}{{{c_{\rm{p}}}}}\nabla T} \right) + {S_{\rm{T}}}, $ | (3) |
式中:T为流体的绝对温度;cp为流体的比热容;k为流体的传热系数;ST为流体的内热源及由于粘性作用流体机械能转化为热能的部分,有时称为粘性耗散项。
式(1)、(2)、(3)即为控制流体流动的微分方程,计算流体动力学的求解过程本质上就是解上述偏微分方程组。
1.2 控制微分方程的一般解法无论是流体流动问题还是流体热传导问题,无论是稳态问题还是瞬态问题,CFD的求解过程如下:
1) 建立控制微分方程,确定初边值条件;
2) 划分计算网格,生成计算节点;
3) 建立离散方程,代入初边值条件;
4) 给定求解控制参数,求解离散方程;
5) 判断解是否收敛。否,转到2);是,转到6);
6) 显示输出计算结果。
可以看出,CFD本质上就是求解式(1)、式(3)的偏微分方程组,而重点难点在于求解域网格的剖分。在一般情况下,传统的网格技术可以很好模拟流体流动问题(比如物体的气动力特性问题),然而对于某些特定的问题(如网格大变形问题),即使数值方法精度再高,如果网格条件与实际问题不匹配,那么得到的数值解也会完全失真。也就是说网格技术对偏微分方程数值解的精确性起着和数值方法同样重要的作用。
2 移动网格技术 2.1 移动网格技术的优势及基本思想移动网格技术作为自适应网格的一种, 最初是由Liao[5]在1992年提出来的,后来被一些学者广泛应用于偏微分方程领域,并取得了一定的效果[6-7]。在网格大变形的流体问题计算中,传统的Lagrange法与Euler法存在缺陷:Lagrange法虽然具有能精确分辨物质界面的优点,但大形变引起的网格相交会导致计算中断;在Euler法中,虽然网格的几何形状较好,但边界处的界面跟踪、混合网格、重构等问题较难处理。移动网格方法是求解发展方程的一种方法,它根据物理解的变化,随时调整网格的疏密和形状。移动网格法既可以精确分辨物质界面又可以保持网格的几何特性,因此在求解网格大变形问题时具有不可比拟的优点。移动网格的特色是,在求解区域内以解的特征决定网格的特征,并且在求解过程中不断更新网格,使之自动与解相匹配。为了实现这一过程,就要用到一种基于调和映射的移动网格方法[8-9],这种方法的基本思想是:将网格变形和控制微分方程的求解完全分开,从而只需构造一个适合问题的控制函数即可。在这个过程中需要引进一个逻辑区域,网格的移动通过由物理区域到逻辑区域的变换实现,物理区域就是需要求解的实际流体区域。
2.2 调和映射移动网格方法最关键也是最困难的一点的就是要找到满足一定条件的网格映射或网格变换。调和映射是Fuller在上世纪40年代提出来的,后来广泛应用于数学物理领域,也用到了自适应网格领域[10],调和映射定下如下:
对于2个n维计算区域Dp和DL,给定一个光滑的映射:ξ:Dp→DL,它的能量密度为
| $ e\left( \xi \right)\left( x \right) = \frac{1}{2}{\left| {d\xi } \right|^2}\left( x \right),\;\;\;x \in {D_{\rm{p}}},e\left( \xi \right) \in {C^\infty }\left( {{D_{\rm{p}}}} \right)。$ | (4) |
映射ξ的能量就是能量密度的积分
| $ E\left( \xi \right) = \int_{{D_p}} {\frac{1}{2}{{\left| {d\xi } \right|}^2}\left( x \right){\rm{d}}x} , $ | (5) |
式中:Dp、DL分别为计算区域的物理区域和逻辑区域。
能量泛函:E:C∞(Dp、DL)→R的临界点就称为调和映射。能量泛函的Lagrange-Euler方程为
| $ \Delta {\xi ^k} + {G^{ij}}\mathit{\Gamma }_{\alpha \beta }^k\frac{{\partial {\xi ^\alpha }}}{{\partial {x^i}}}\frac{{\partial {\xi ^\beta }}}{{\partial {x^j}}} = 0, $ | (6) |
式中:Δ为Laplace-Beltrimi算子;Gij为局部坐标系xn的Rieman度量;Γαβk为Dp上的联络系数。
从以上推导可知,调和映射本质上是调和函数与极小子流形的推广[11]。Hamilton, Schoen等建立了比较完善的调和映射存在性和唯一性的定理[12-13],并给出了相应的条件。存在唯一性的结论有利于避免网格互相交错缠绕而导致的计算中断。
2.3 控制函数控制函数其实就是求解域上给定的一个正定的函数矩阵,它是生成移动网格的关键因素。控制函数在变分形式可以用来控制网格的质量,并使网格与求解域的物理解耦合起来,这时控制函数就可以用来度量物理区域上的物理量,物理区域上的度量矩阵可取为控制函数的逆。对于控制函数构造的一般原则是:用数值解的梯度来判断求解域中哪个部分的解改变得快,从而就将网格集中在哪里。利用梯度构造的控制函数的一般形式取为
| $ M = \sqrt {1 + \alpha {{\left| u \right|}^2} + \beta {{\left| {\nabla u} \right|}^2} + \gamma {{\left| {{\nabla ^2}u} \right|}^2}\mathit{\boldsymbol{I}}} , $ | (7) |
式中,α、β、γ为正参数;I为单位矩阵;▽为Hamilton算子。
也有将控制函数与误差估计联系在一起构造控制函数的[14]:
| $ G\left( {x,{t_n}} \right) = \sqrt {\left. {1 + \alpha {{\left( {\bar e\left( {x,{t_n}} \right)/{{\left\| {\bar e\left( {x,{t_n}} \right)} \right\|}_\Omega }} \right)}^2}} \right)} \mathit{\boldsymbol{I}}, $ | (8) |
式中,e(x, tn)为关于误差指标e的函数。
还有利用方向导数构造控制函数[15]:
| $ f\left( {{X_i},t} \right) = g\left( {\partial u/\partial l} \right)\mathit{\boldsymbol{I}}。$ | (9) |
它们的原理和关于梯度的控制函数是一样的。
2.4 网格的移动从求解域的物理区域Dp到逻辑区域DL变换的具体实现方法,是在选定了逻辑区域DL和给定了流场DP上的一个一致剖分T(设其节点为xi)后,先确定在流体在边界上的映射的情况,然后将这个边界上的映射记为给定的一个同胚φ在边界上的限制,再通过解Possion方程组
| $ \Delta {\xi ^k} = 0,{\xi ^k}\left| {_{\partial {D_{\rm{p}}}}} \right. = \varphi \left| {_{\partial {D_{\rm{p}}}}} \right.,\left( {1 \le k \le n} \right)。$ | (10) |
根据上式就可以得到一个逻辑网格了,式(10)的解将求解域的物理区域Euclid度量变换成了逻辑区域的诱导度量
要完成网格的移动,最终还是要通过移动的向量场来实现。假设t时刻对应的物理网格为Tt(其结点记为Xti),通过计算控制函数M,在网格Tt上求解椭圆方程组
| $ \frac{\partial }{{\partial {x^i}}}\left( {{G^{ij}}\frac{{\partial {\xi ^k}}}{{\partial {x^j}}}} \right) = 0,\xi \left| {_{\partial {D_{\rm{p}}}}} \right. = {\xi _b}。$ | (11) |
可得到流场网格的节点Xti在调和映射下的像ξti,进而得到它与逻辑网格之间的差δξi*=ξi-ξti。利用逻辑网格到流场网格上变换的一阶导数,将它插值为流场网格上的一个分片性的向量场,从而得到流场上的每个节点的移动方向δXi, *,于是流场网格的节点更新为
| $ {X_t}: = X_t^i + \eta \cdot \delta {X^{i, * }}, $ | (12) |
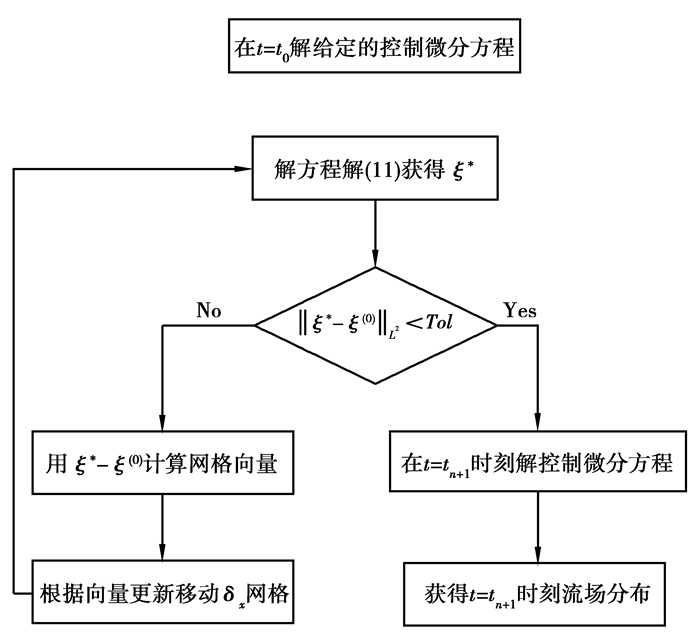
式中,η为网格移动的步长。这样求解域的网格就达到了更新的目的。移动网格法应用于CFD数值仿真的程序流程如图 1所示。
|
图 1 移动网格法应用于CFD的程序流程图 |
可以看出,移动网格求解CFD过程由2部分构成:网格移动和时间步进。网格移动本质上就是建立在流场网格(物理区域)与逻辑网格之间的调和映射的一个迭代过程。在这个过程中,网格逐步向调和映射逼近,最终得到需要的实际流场。在数值计算过程中,逻辑区域的初始网格保持固定,这个网格不用来接任何偏微分方程,但是它与方程(11)的解的误差用来实现网格的移动。
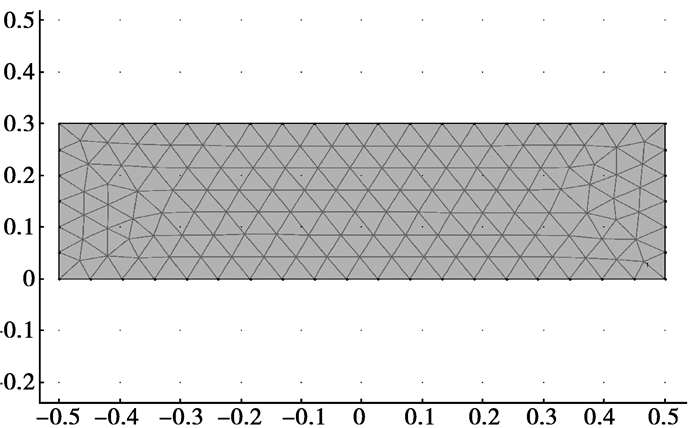
3 数值仿真算例 3.1 模型背景当油箱做倾斜晃动的过程中,油箱内的油会在重力矢量的作用下来回晃动,由于表面没有约束,导致其变形很大而且非常不规则,采用传统均匀固定的网格几乎无法求解,然而用移动网格技术可以很好的解决此类问题。本案例借助多物理场耦合软件COMSOL Multiphysics中的计算流体动力学模块(CFD模块)和移动网格模块(ALE模块)来仿真油箱中油的运动规律。COMSOL Multiphysics作为全球第一款真正的多物理场耦合分析软件,采用基于偏微分方程建模的方式,因此在处理移动网格和控制方程耦合问题时有它特有的优势。模型参数为:矩形油箱,高度足够高,内部装有一定量的油,求解域长1 m,宽0.3 m,液体密度取1 270 kg/m3, 粘度取1.49 Pa·s,油箱摆动的最大倾角为4°。流体为牛顿流体,模型采用单向流的层流模型,不考虑导热过程。根据程序本身强大的网格划分功能自由剖分成三角形网格,其求解域的初始网格如图 2所示。
|
图 2 求解域初始网格模型 |
控制方程的求解域确定后,接下来就是要设置控制微分方程及移动网格的边界条件。
流体控制微分方程边界条件的确定:矩形左边界、右边界及下边界为滑动壁面边界条件;上边界为自由液面,为开边界,法向应力为零。
移动网格边界条件的确定:对于矩形区域的左边界和右边界,指定网格位移在水平方向为零,竖直方向自由变形;对于下边界,指定网格在水平方向及竖直方向都为零;对于自由液面,采用边界坐标系,指定网格法向的速度为“u·nx+v·ny”,即把网格的水平速度u和竖直速度v分解到法向, 切向速度不做约束。
通过以上设置,其实就是将移动网格和求解区域耦合起来,在进行瞬态分析时,每经过一个时间子步,网格就会产生一个变形,更新之后的网格模型又会成为下一个时间子步的初始条件,这样往复下去,就可以得到一段时间内网格的变形情况。
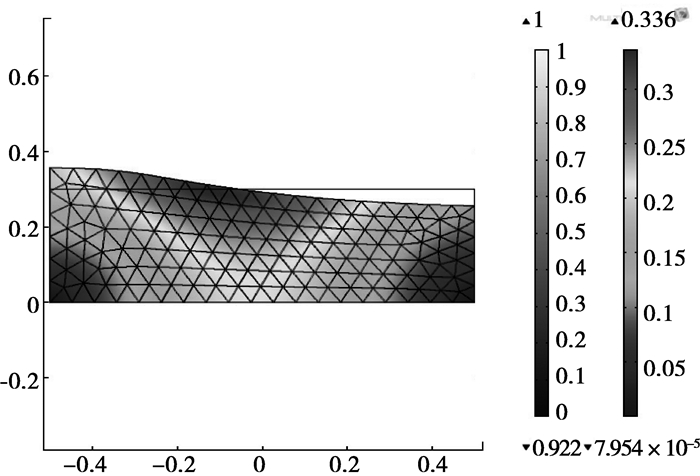
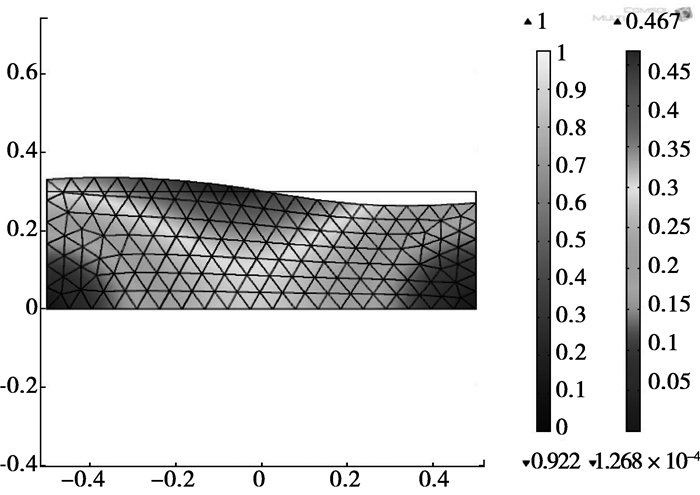
3.3 仿真结果及分析采用软件提供的瞬态求解器求解,仿真时间为6 s,时间步长为0.1 s。其中时间t分别为1、1.3、1.6 s的速度矢量及网格变形如图 3~图 5所示。
|
图 3 t=1 s网格分布及速度矢量图 |
|
图 4 t=1.3 s网格分布及速度矢量图 |
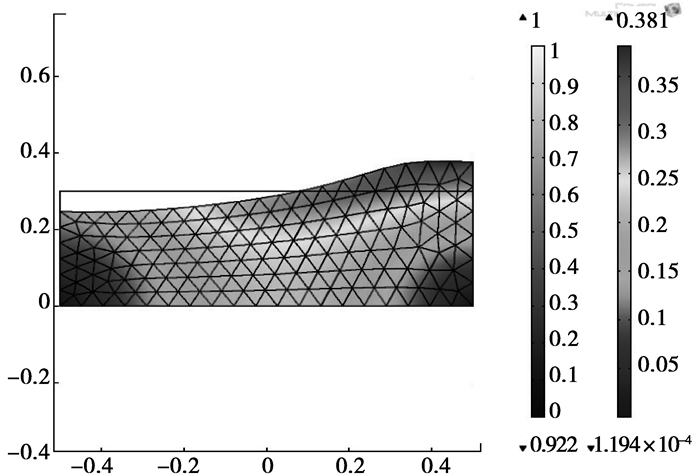
|
图 5 t=1.6 s网格分布及速度矢量图 |
通过移动网格技术,还可以追踪液体自由液面的运动情况,如图 6所示,矩形左端液面高程和右端液面高程随时间变化的关系。
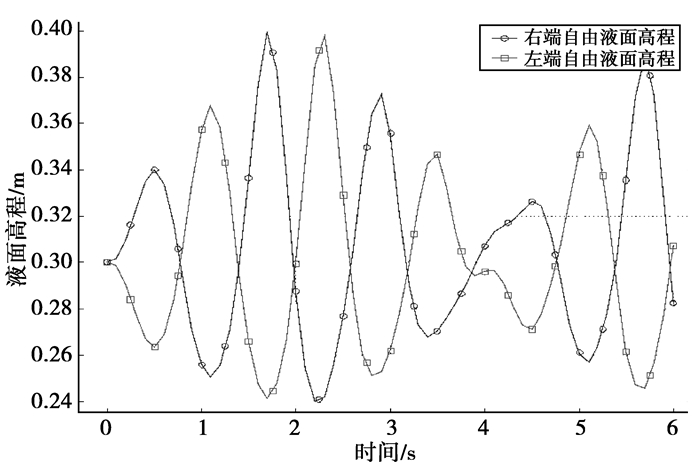
|
图 6 求解域左右液面高程图 |
从图 3~图 5可以看出,在油箱的晃动过程中,油箱内的液体在重力矢量的作用下也在来回晃动。从图 6可以看出,当左端自由液面高程达到波峰时,右端自由液面高程达到波谷,反之亦然,左端液面高程与右端的液面高程正好相差一个相位,这与实际情况是相符的。通过该数值算例可以得出如下结论。
1) 将移动网格技术应用于CFD仿真计算,可以很好的模拟流体网格大变形的情况,较为真实地反应流体流动。
2) 在网格的变形过程中,网格的结构没有发生改变,网格的加密和稀疏化是自动实现的。而且在移动过程中,网格之间没有出现缠绕畸变等情况,保证了仿真结果的正确性和精度。
3) 对于网格的移动,只是网格节点位置的调整,而节点数和网格节点的数据结构并不会发生改变,因此移动网格在保证计算精度的同时,又不额外的增加计算量,大大节省计算机的内存开销,缩短了计算时间,程序的调试也变得简单很多。
4 结语CFD问题可以最终归结为求解偏微分方程的问题,因此可以引入一种强有力的解偏微分方程的工具:移动网格技术。移动网格具有传统固定网格无法比拟的优点,将其应用于CFD的数值仿真领域,可以很好地解决广泛存在于自然界的流体区域大变形问题,而且在仿真过程中,不改变节点和网格数量,对计算机资源没有额外开销。因此,移动网格技术在CFD的数值仿真研究领域有着广泛的应用前景。
| [1] | Anderson J D. 计算流体力学基础及其应用[M]. 吴颂平, 刘赵淼, 译. 武汉: 机械工业出版社, 2007. |
| [2] | 朱红钧, 林元华, 谢龙汉. FLUENT流体分析及仿真实用教程[M]. 北京: 人民邮电出版社, 2010. |
| [3] | Sun D K, Owen J S, Wright N G, et al. Fluid-structure interaction of prismatic line-like structures, using LES and block-iterative coupling[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(6/7): 840–858. |
| [4] | Ju L L, Du Q. A finite volume method on general surfaces and its error estimates[J]. Journal of Mathematical Analysis and Applications, 2009, 352(2): 645–668. DOI:10.1016/j.jmaa.2008.11.022 |
| [5] | Liao G J, Anderson D. A new approach to grid genertion[J]. Applicable analysis, 1992, 44(3/4): 285–298. |
| [6] | Tuković Ž, Jasak H. A moving mesh finite volume interface tracking method for surface tension dominated interfacial fluid flow[J]. Computers & Fluids, 2012, 55(15): 70–84. |
| [7] | Wan D C, Turek S. Fictitious boundary and moving mesh methods for the numerical simulation of rigid particulate flows[J]. Journal of Computational Physics, 2007, 222(1): 28–56. DOI:10.1016/j.jcp.2006.06.002 |
| [8] | Iwaniec T, Kovalev L V, Onninen J. The harmonic mapping problem and affine capacity[J]. Proceedings of the Royal Society of Edinburgh:Section A Mathematics, 2011, 141(5): 1017–1030. DOI:10.1017/S0308210510000107 |
| [9] | Li X, Guo X H, Wang H Y, et al. Meshless harmonic volumetric mapping using fundamental solution methods[J]. IEEE Transactions on Automation Science and Engineering, 2009, 6(3): 409–422. DOI:10.1109/TASE.2009.2014735 |
| [10] | Barrera-Sánchez P, Noda L C, Francisco J, et al. Adaptive discrete harmonic grid generation[J]. Mathematics and Computers in Simulation, 2009, 79(6): 1792–1809. DOI:10.1016/j.matcom.2007.04.015 |
| [11] | 李阳贵. 移动网格方法在非定常渗流计算中的应用[D]. 湖南: 南华大学硕士学位论文, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10540-2010254653.htm |
| [12] | Hamilton R S. Harmonic maps of manifolds with boundary:lecture notes in mathematics[M]. Berlin: Springer-Verlag, 1975. |
| [13] | Schoen R, Yau S T. On univalent harmonic maps between surfaces[J]. Inventiones Mathematicae, 1978, 44(3): 265–278. DOI:10.1007/BF01403164 |
| [14] | Cao W M, Huang W Z, Russell R D. An error indicator monitor function for an r-adaptive finite element method[J]. Journal of Computational Physics, 2001, 170(2): 871–892. DOI:10.1006/jcph.2001.6770 |
| [15] |
王礼广, 蔡放, 熊岳山.
一种新的基于方向导数的二维自适应网格生成算法[J]. 国防科技大学学报, 2007, 29(6): 126–130.
WANG Liguang, CAI Fang, XIONG Yueshan. A new algorithm of mesh generation for 2-D adaptive mesh based on directional derivatives[J]. Journal of National University of Defense Technology, 2007, 29(6): 126–130. (in Chinese) |
| [16] | Cao W M, Huang W Z, Russell R D. Comparison of two-dimensional r-adaptive finite element methods using various error indicators[J]. |
 2013, Vol. 36
2013, Vol. 36


