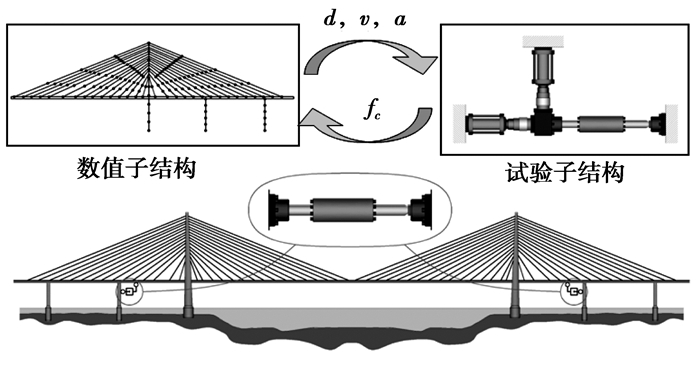
随着计算机技术和计算方法的飞速发展，结构抗震的数值分析方法也越来越先进，如有限元方法、边界元方法及数值积分方法等，可以很容易地进行复杂结构的地震反应模拟。但是地震作用下，结构局部表现出非线性特性以及智能结构的率相关特性，使现有数值模拟方法的计算结果受到限制。实时子结构试验是近年来得到快速发展的一种新型试验方法，该方法只需要对结构中物理特性复杂或不易用数值方法模拟的部分进行实时加载，而其余部分采用数值积分方法进行模拟(如图 1所示)，大大减小了物理模型的试验规模，可以方便进行大比例尺甚至足尺试验。

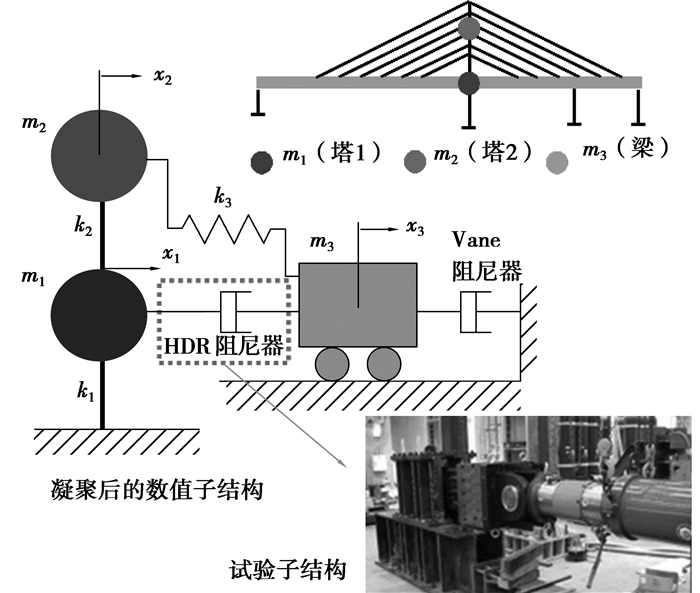
目前实时子结构试验的研究仍处于起步阶段，已有的研究成果^[1-4]局限于一些小规模的试验，大部分试验中物理子结构和数值子结构的耦联只通过单个作动器实现；而数值模型也很简单，多为一个或几个自由度的线性模型。实时子结构试验需要以实际荷载速率进行加载，这意味着每一个加载过程必须在几个毫秒内完成，这就要求数值子结构的计算在非常短且固定的时间内完成。而对复杂结构进行实时子结构试验时，数值子结构大都有几十个到上千个自由度，有时还需要考虑非线性的数值子结构模型。现有的积分方法很难实现，大多是通过自由度凝聚把复杂结构转化几个自由度的线性模型^[5](如图 2所示)，这样也降低了最终结果的精度。解决该问题的另一可行方法是采用多步长的耦合积分方法，采用不同的步长来进行数值子结构和试验子结构的积分。

耦合积分方法最早应用于多物理(Multi-Physics)问题，如流固耦合问题^[6]。随着高性能并行计算机及混合模拟技术^[7]的出现，不少学者开始研究：如何把一个大规模的模拟或计算任务分解成若干个小问题；然后采用不同的积分过程或者积分方法进行有针对性的求解。这样耦合积分方法得到更为广泛的应用^[8]。近年来，耦合积分方法已应用于连续拟动力试验^[9]。在多体动力学领域，也有学者尝试把它应用于实时模拟^[10]，如硬件在环试验(hardware-in-the-loop testing)。但在实时子结构试验上应用较少。

笔者基于Rosenbrock积分方法提出了一种多步长的耦合积分方法，并进行了稳定性及精度分析。具体地讲，首先简单介绍了实时Rosenbrock积分方法；在此基础上，提出了一种耦合积分方法；然后采用单自由度的验证系统对该耦合积分方法的精度和稳定性进行了数值分析；最后对三自由度(界面两自由度)验证模型进行了数值模拟，为其在实时子结构试验上的应用提供了理论依据。

1 Rosenbrock积分方法简介

Rosenbrock积分方法在一阶刚性系统初值问题的求解方面应用广泛。该方法是在隐式Runge-Kutta方法基础上采用内嵌牛顿迭代来实现显示化的，它既保持了隐式Runge-Kutta方法的稳定性，又避免了迭代。这类方法既不属于显式积分方法也不属于隐式积分方法，在数学上被称为线性隐式积分方法^[11]。考虑n维非线性常微分方程组初值问题：

$ \dot y = f\left( {y,t} \right),y\left( {{t_0}} \right) = {y_0}, $

(1)

假设f(y, t)具有以下讨论所需要的各阶导数。把所要求的总计算时间等分为N个步长Δt的时间单元。记t_k=kΔt，用y_k表示在t_k时刻的状态变量值。为求解t_k+1的状态变量值y_k+1，应用s级Rosenbrock积分方法可得

$ \begin{array}{*{20}{c}} {{y_{k + 1}} = {y_k} + \sum\limits_{i = 1}^s {{b_i}{k_i}} ,}\\ {{k_i} = {{\left[ {\mathit{\boldsymbol{I}} - {\gamma _{ii}}\Delta tJ} \right]}^{ - 1}} \cdot \left[ {f\left( {{y_k} + \sum\limits_{j = 1}^{i - 1} {{\alpha _{ij}}{k_j}} ,{t_k} + } \right.} \right.}\\ {\left. {\left. {{\alpha _i}\Delta t} \right)\Delta t + J\sum\limits_{j = 1}^{i - 1} {{\gamma _{ij}}{k_j}\Delta t} } \right],} \end{array} $

(2)

其中：I为n×n的单位矩阵；α_i、α_ij、γ_ij和b_i属于算法系数。这些系数决定了该积分方法的数值特性，比如精度阶数、稳定性、数值阻尼特性以及兼时性(real-time compatibility)^[12]。对于线性问题而言，J=∂f/∂y为Jacobian矩阵；而对于非线性问题而言，J为近似的Jacobian矩阵，可采用t_k时刻的Jacobian矩阵，即J=∂f/∂y|_tk。同时该方法还包括s个未知量k_i，这就需要进行s次求逆矩阵[I-γ_iiΔtJ]^-1。为简化计算，假设γ₁₁=γ₂₂=…=γ_ss=γ。

在这种线性隐式Rosenbrock积分方法基础上，Bursi等^[12]提出了3种兼时积分算法。考虑到精度需求和应用方便，文中只分析具有二阶精度(满足工程需要)的LSRT2法(l-stable real-time compatible method)。考虑到兼时性、二阶精度和L稳定性的需要，算法参数取值为

$ \begin{array}{*{20}{c}} {{\alpha _2} = {\alpha _{21}} = 1/2,{b_1} = 0,{b_2} = 1,}\\ {{\gamma _{21}} = - \gamma ,\gamma = 1 \pm \sqrt 2 /2。} \end{array} $

(3)

考虑这些参数，LSRT2方法可写为

$ {k_1} = {\left[ {\mathit{\boldsymbol{I}} - \gamma \Delta t\mathit{\boldsymbol{J}}} \right]^{ - 1}}{f_k}\Delta t,{y_{k + \frac{1}{2}}} = {y_k} + \frac{1}{2}{k_1}, $

(4)

$ \begin{array}{*{20}{c}} {{k_2} = {{\left[ {\mathit{\boldsymbol{I}} - \gamma \Delta t\mathit{\boldsymbol{J}}} \right]}^{ - 1}}\left( {{f_{k + \frac{1}{2}}} - \mathit{\boldsymbol{J}}\gamma {k_1}} \right)\Delta t,}\\ {{y_{k + 1}} = {y_k} + {k_2}。} \end{array} $

(5)

将Rosenbrock积分方法推广到结构动力学问题上，考虑空间离散后的一般运动方程：

$ \mathit{\boldsymbol{M}}\ddot u\left( t \right) + \mathit{\boldsymbol{R}}\left( {u\left( t \right),\dot u\left( t \right)} \right) = P\left( t \right), $

(6)

对线性问题有

$ \mathit{\boldsymbol{R}}\left( {u\left( t \right),\dot u\left( t \right)} \right) = \mathit{\boldsymbol{C}}\dot u\left( t \right) + \mathit{\boldsymbol{K}}u\left( t \right), $

(7)

其中：M是质量矩阵，K是刚度阵，C为粘性阻尼阵，都是对称的，且一般M正定，K、C正定或半正定。u(t), $\dot u$(t)和$\ddot u$(t)分别是结构系统的位移、速度和加速度；P(t)是随时间变化的激励力向量。为采用一阶积分格式的LSRT2法，将二阶动力方程(6)转化为一阶形式：

$ \dot y = f\left( {y,t} \right) = \left\{ {\begin{array}{*{20}{c}} {\dot u}\\ {P - R\left( {u,\dot u} \right)} \end{array}} \right\},y = \left\{ {\begin{array}{*{20}{c}} u\\ {\dot u} \end{array}} \right\}。$

(8)

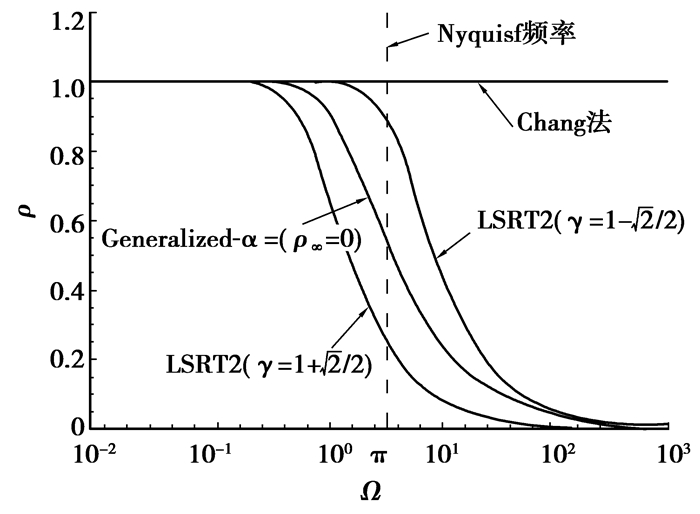
其中y为结构的状态变量。文献[7]基于二阶标量验证方法对LSRT2法进行了谱分析。图 1绘制了LSRT2法、Generalized-α法和Chang法的谱曲线。即谱半径ρ和采样频率Ω(Ω=ωΔt)的关系曲线。如图 3所示。LSRT法在整个Ω区间内，谱半径都小于等于1；在高频区间(after Nyquist frequency)谱半径随Ω的增大趋近于0；在低频区间(before Nyquist frequency)谱半径随Ω的减小趋近于1。这表明该方法具有高频响应过滤特性，且不影响低频响应的精度。

2 耦合积分方法及其并行格式

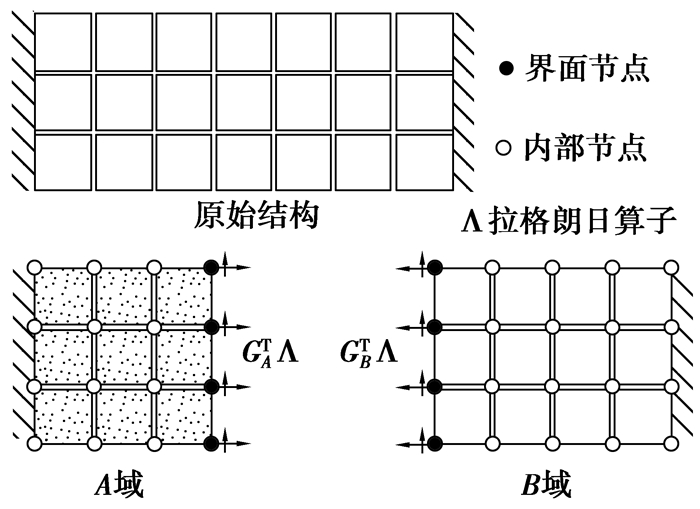
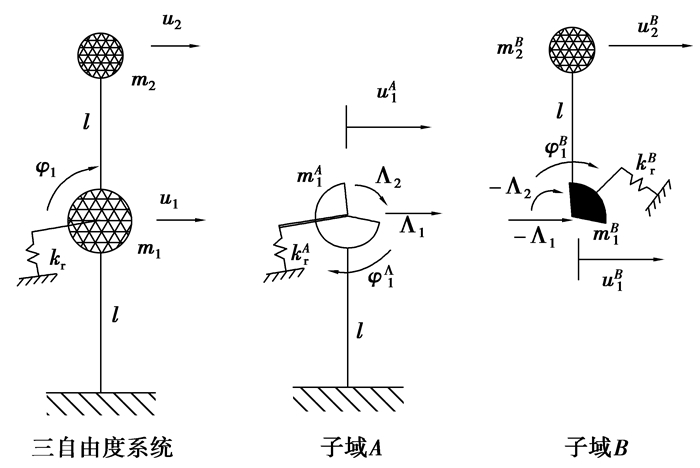
对复杂结构或复杂问题进行分析时，不同区域的非线性程度可能截然不同(如图 4所示)。有时，为达到预期的精度，计算模型中不同的区域需要截然不同的网格划分方式。对于特定问题，分析中涉及不同材料(如钢木组合结构、钢混凝土组合结构等)、不同特性的子系统(如结构控制问题等)。这些情况下若采用直接积分方法(如Newmark法、Runge-Kutta法)对整个模型进行求解，即所谓的整体积分方式，可能所需要的积分步长会非常小，从而导致计算量很大。这主要是因为所采用的积分步长要满足整个系统的计算精度和稳定性的要求。对于这类问题，不少学者借助耦合积分方法：对不同的区域采用不同的积分方法或不同的积分步长，以期获得更好的计算效率或计算精度。这些采用不同积分步长的方法也叫子步法(subcycling)或多步长方法(multi-time-step method)。文中采用有限元分裂内联法^[14](finite element tearing and interconnection，FETI)进行区域分解。如图 5所示，采用FETI法将一个两端固支的梁分割成A域和B域，分割后的两子域的藕联是通过界面上的力平衡和运动变量(位移、速度或加速度)的协调来实现的。

各子域的运动方程及其加速度约束方程可以表示成

$ \left. \begin{array}{l} {\mathit{\boldsymbol{M}}_A}{{\ddot u}^A} + {R^A}\left( {{u^A},{{\dot u}^A}} \right) = {P^A} + \mathit{\boldsymbol{G}}_A^T\Lambda \\ {\mathit{\boldsymbol{M}}_B}{{\ddot u}^B} + {R^B}\left( {{u^B},{{\dot u}^B}} \right) = {P^B} + \mathit{\boldsymbol{G}}_B^T\Lambda \\ {\mathit{\boldsymbol{G}}_A}{{\ddot u}^A} + {\mathit{\boldsymbol{G}}_B}{{\ddot u}^B} = 0 \end{array} \right\}, $

(9)

方程(9)就是典型的Index-1代数微分方程^[8]。式中Λ是拉格朗日算子；G_A是布尔矩阵(boolean matrix)，它用于列出界面节点的运动变量，而它的转置则用于列出界面力。因此，式(9)中的代数方程表示的是界面上的运动协调方程，而G_A^TΛ和G_B^TΛ分别表示A域和B域的界面节点力向量，它们用在方程(9)中以表征界面的力平衡。考虑到采用一阶积分方法，故采用降阶处理：

$ \left. \begin{array}{l} {\mathit{\boldsymbol{A}}_A}{{\dot y}^A} = {F^A} + C_A^T\Lambda \\ {\mathit{\boldsymbol{A}}_B}{{\dot y}^B} = {F^B} + C_B^T\Lambda \\ {C_A}{{\dot y}^A} + {C_B}{{\dot y}^B} = 0 \end{array} \right\}, $

(10)

其中，

$ {\mathit{\boldsymbol{A}}_A} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_A}}&0\\ 0&{{\mathit{\boldsymbol{M}}_A}} \end{array}} \right],{\mathit{\boldsymbol{A}}_B} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_B}}&0\\ 0&{{\mathit{\boldsymbol{M}}_B}} \end{array}} \right], $

$ {y^A} = \left\{ {\begin{array}{*{20}{c}} {{u_A}}\\ {{{\dot u}_A}} \end{array}} \right\},{y^B} = \left\{ {\begin{array}{*{20}{c}} {{u_B}}\\ {{{\dot u}_B}} \end{array}} \right\},{\mathit{\boldsymbol{C}}_A} = \left[ {\begin{array}{*{20}{c}} 0\\ {{\mathit{\boldsymbol{G}}_A}} \end{array}} \right],{\mathit{\boldsymbol{C}}_B} = \left[ {\begin{array}{*{20}{c}} 0\\ {{\mathit{\boldsymbol{G}}_B}} \end{array}} \right], $

$ {F^A} = \left\{ {\begin{array}{*{20}{c}} 0\\ {{P^A} - {R^A}\left( {{u^A},{{\dot u}^A}} \right)} \end{array}} \right\},{F^B} = \left\{ {\begin{array}{*{20}{c}} 0\\ {{P^B} - {R^B}\left( {{u^B},{{\dot u}^B}} \right)} \end{array}} \right\}。$

把公式(10)的常微分方程带入代数方程，可以求解拉格朗日算子：

$ \Lambda = - {H^{ - 1}}\left( {{\mathit{\boldsymbol{C}}_A}\mathit{\boldsymbol{A}}_A^{ - 1}{F^A} + {\mathit{\boldsymbol{C}}_B}\mathit{\boldsymbol{A}}_B^{ - 1}{F^B}} \right), $

(11)

其中，H=C_AA_A^-1C_A^T+C_BA_B^-1C_B^T。

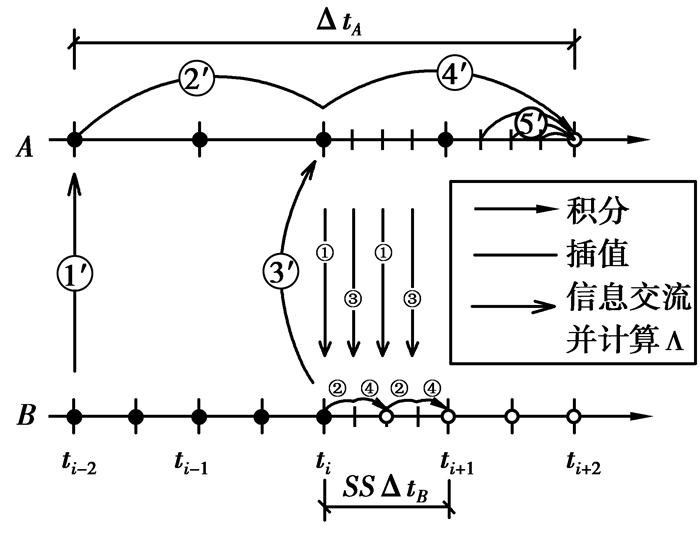
文中所提出的耦合积分方法具有显式特性，主要是由于显式的拉格朗日算子(11)以及Rosenbrock的显式求解格式。为满足复杂结构的实时子结构试验及并行模拟的需要，该耦合算法采用线性插值的子步法并设计成并行格式。如图 6所示，A域的积分步长为Δt_A=4·Δt；B域的积分步长为$\Delta {t_B} = \frac{{\Delta t}}{{ss}}$，其中Δt是系统步长。

该方法详细的计算步骤如下：

1) 计算F_i-2^A和F_i-2^B并求解Λ_i-2，

$ {\Lambda _{i - 2}} = - {H^{ - 1}}\left( {{\mathit{\boldsymbol{C}}_A}\mathit{\boldsymbol{A}}_A^{ - 1}F_{i - 2}^A + {\mathit{\boldsymbol{C}}_B}\mathit{\boldsymbol{A}}_B^{ - 1}F_{i - 2}^B} \right); $

2) 计算k₁^A并求解A域的状态变量y_i^A，

$ k_1^A = {\left[ {\mathit{\boldsymbol{I}} - 4\Delta t\gamma {\mathit{\boldsymbol{J}}^A}} \right]^{ - 1}}\mathit{\boldsymbol{A}}_A^{ - 1}\left[ {F_{i - 2}^A + \mathit{\boldsymbol{C}}_A^{\rm{T}}{\Lambda _{i - 2}}} \right]4\Delta t, $

$ y_i^A = y_{i - 2}^A + 1/2 \cdot k_1^A; $

3) 计算F_i^A和F_i^B并求解Λ_i，

$ {\Lambda _i} = - {H^{ - 1}}\left( {{\mathit{\boldsymbol{C}}_A}\mathit{\boldsymbol{A}}_A^{ - 1}F_i^A + {\mathit{\boldsymbol{C}}_B}\mathit{\boldsymbol{A}}_B^{ - 1}F_i^B} \right); $

4) 计算k₂^A并求解A域的状态变量y_i+2^A

$ k_2^A = {\left[ {\mathit{\boldsymbol{I}} - 4\Delta t\gamma {\mathit{\boldsymbol{J}}^A}} \right]^{ - 1}}\left\{ {\mathit{\boldsymbol{A}}_A^{ - 1}\left[ {F_i^A + \mathit{\boldsymbol{C}}_A^{\rm{T}}{\Lambda _i}} \right] - \gamma {\mathit{\boldsymbol{J}}^A}k_1^A} \right\}4\Delta t, $

$ y_{i + 2}^A = y_{i - 2}^A + k_2^A; $

5) 采用线性插值的方法计算步内变量

$ y_{i + 1 + \frac{{in}}{{2ss}}}^A = \left( {1 - \frac{{in}}{{2ss}}} \right)y_{i + 1}^A + \frac{{in}}{{2ss}}y_{i + 2}^A $

其中，in=1, 2, …, 2ss。

与此同时，B域的积分包括ss个子步，第j个子步的积分过程如下：

① 计算$F_{i + \frac{{j - 1}}{{ss}}}^A$和$F_{i + \frac{{j - 1}}{{ss}}}^B$并求解${\Lambda _{i + \frac{{j - 1}}{{ss}}}}$，

$ {\Lambda _{i + \frac{{j - 1}}{{ss}}}} = - {H^{ - 1}}\left[ {{\mathit{\boldsymbol{C}}_A}\mathit{\boldsymbol{A}}_A^{ - 1}F_{i + \frac{{j - 1}}{{ss}}}^A + {\mathit{\boldsymbol{C}}_B}\mathit{\boldsymbol{A}}_B^{ - 1}F_{i + \frac{{j - 1}}{{ss}}}^B} \right]。$

② 计算k₁^B并求解B域的状态变量$y_{i + \frac{{2j - 1}}{{2ss}}}^B$，

$ k_1^B = {\left[ {\mathit{\boldsymbol{I}} - \frac{{\Delta t}}{{ss}}\gamma {\mathit{\boldsymbol{J}}^B}} \right]^{ - 1}}\mathit{\boldsymbol{A}}_B^{ - 1}\left[ {F_{i + \frac{{j - 1}}{{ss}}}^B + \mathit{\boldsymbol{C}}_B^{\rm{T}}{\Lambda _{i + \frac{{j - 1}}{{ss}}}}} \right]\frac{{\Delta t}}{{ss}}, $

$ y_{i + \frac{{2j - 1}}{{ss}}}^B = y_{i + \frac{{j - 1}}{{ss}}}^B + \frac{1}{2}k_1^B $

(3) 计算$F_{i + \frac{{2j - 1}}{{2ss}}}^A$和$F_{i + \frac{{2j - 1}}{{2ss}}}^B$并求解${\Lambda _{i + \frac{{2j - 1}}{{2ss}}}}$，

$ {\Lambda _{i + \frac{{2j - 1}}{{ss}}}} = - {H^{ - 1}}\left[ {{\mathit{\boldsymbol{C}}_A}\mathit{\boldsymbol{A}}_A^{ - 1}F_{i + \frac{{2j - 1}}{{ss}}}^A + {\mathit{\boldsymbol{C}}_B}\mathit{\boldsymbol{A}}_B^{ - 1}F_{i + \frac{{2j - 1}}{{ss}}}^B} \right]。$

(4) 计算k₂^B并求解B域的变量$y_{i + \frac{{j + 1}}{{ss}}}^B$，

$ \begin{array}{l} k_2^B = \\ {\left[ {\mathit{\boldsymbol{I}} - \frac{{\Delta t}}{{ss}}\gamma {\mathit{\boldsymbol{J}}^B}} \right]^{ - 1}}\left\{ {\mathit{\boldsymbol{A}}_B^{ - 1}\left[ {F_{i + \frac{{2j - 1}}{{ss}}}^B + \mathit{\boldsymbol{C}}_B^{\rm{T}}{\Lambda _{i + \frac{{2j - 1}}{{ss}}}}} \right] - \gamma {\mathit{\boldsymbol{J}}^B}k_1^B} \right\}\frac{{\Delta t}}{{ss}}, \end{array} $

$ y_{i + \frac{j}{{ss}}}^B = y_{i + \frac{{j - 1}}{{ss}}}^B + k_2^B。$

以上为一个系统积分步长的计算过程。该过程可以做到独立计算甚至并行计算是因为：A域的步长放大了4倍，这样一方面可以采用B域前几步的界面节点上的状态变量；同时另一方面又可以为B域下一步的求解提供了步内状态变量。另外，需要指出的是：这过程不是自启动(self-starting)，这里就需要一个启动算法来计算所需的Δt和2·Δt时刻的状态变量。以下的数值模拟均采用等步长的耦合积分方法作为启动算法^[15]。

3 耦合积分方法的收敛性分析

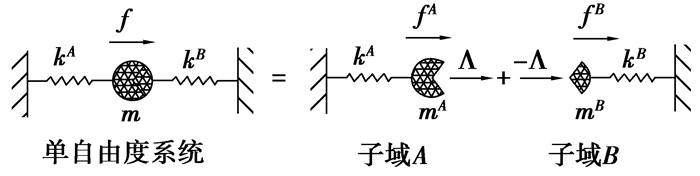
对于数值积分方法而言，收敛性(即稳定性和精度)是最受关注的问题。为分析该耦合方法的收敛性，文中选取单自由度分离质量模型^[16](如图 7所示)。

首先进行稳定性分析。假设m=m_A+m_B=1，k=k_A+k_B=1，并定义参数

$ {b_1} = \frac{{{m_A}}}{{{m_B}}} = \frac{{{k_B}}}{{{k_A}}}。$

(12)

为了分析该耦合方法的算法耗散特性，假设系统阻尼和外力均为0。将耦合积分方法应用于图 7所示的验证模型，分别在相邻不同的时刻应用该算法可得如下一般形式：

$ {x_{k + 1}} = \mathit{\boldsymbol{R}}{x_k}, $

(13)

式中R为放大矩阵。这里通过分析R的特征值来分析该算法的谱稳定性。该积分方法不是自启动算法，而且它包含子步思想。对于这种复杂算法的谱稳定性分析，其关键在于选择合适的x_k向量。在前述的积分过程中，所需要的输入变量为y_i-2^A、y_i-2^B、y_i^A、y_i^B和y_i+1^A，而所输出的变量为y_i-1^A和y_i-1^B。为分析其放大特性，应选取

$ \begin{array}{*{20}{c}} {{x_k} = \left\{ {\begin{array}{*{20}{c}} {{{\left( {y_{i - 2}^A} \right)}^{\rm{T}}}}&{{{\left( {y_{i - 2}^B} \right)}^{\rm{T}}}}&{{{\left( {y_{i - 1}^A} \right)}^{\rm{T}}}} \end{array}} \right.}\\ {{{\left. {\begin{array}{*{20}{c}} {{{\left( {y_{i - 1}^B} \right)}^{\rm{T}}}}&{{{\left( {y_i^A} \right)}^{\rm{T}}}}&{{{\left( {y_i^B} \right)}^{\rm{T}}}}&{{{\left( {y_{i + 1}^A} \right)}^{\rm{T}}}} \end{array}} \right\}}^T}} \end{array} $

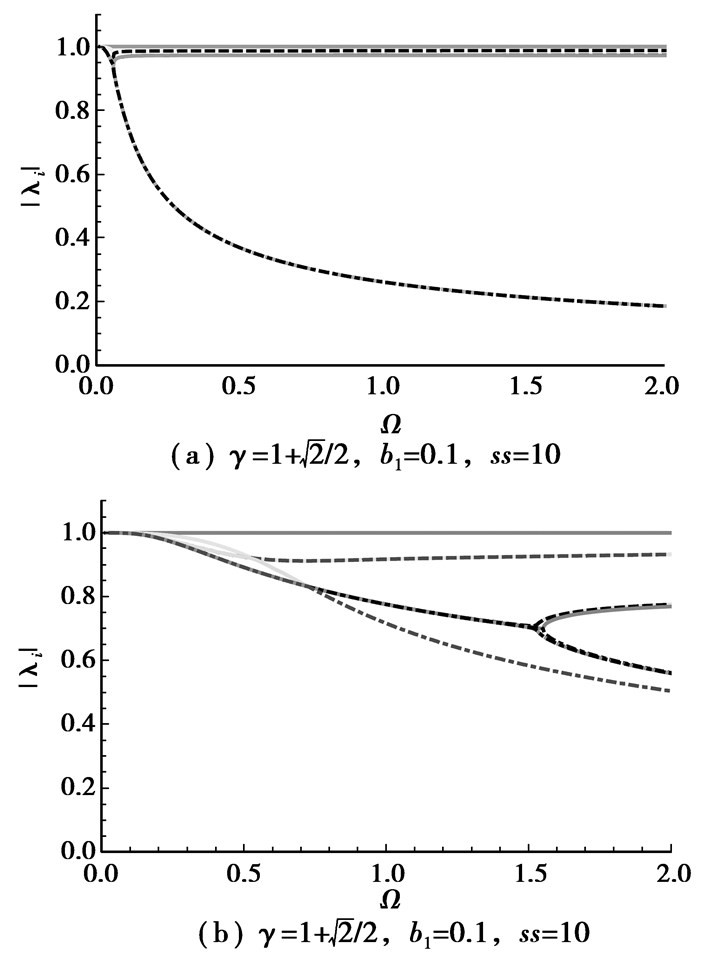
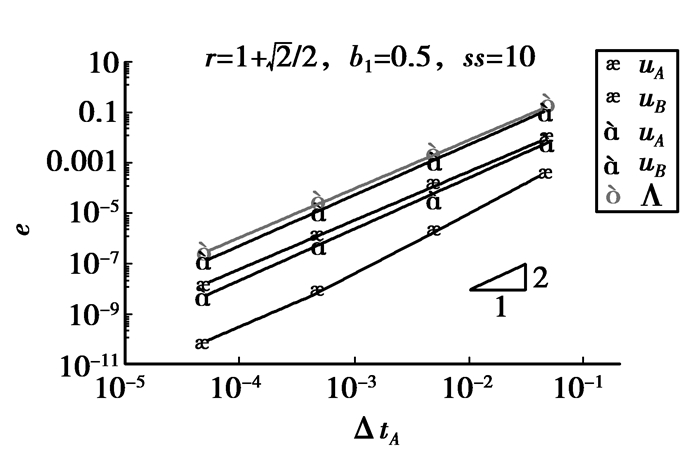
因此，R矩阵的维数为14。它特征值的绝对值与采样频率$\Omega = \sqrt {k/m} \Delta {t_A}$的关系曲线如图 8所示。R矩阵的非零特征值的个数为10，其中，4对共轭复数，2个为实数(其中有1个特征值恒为1)。通过不同情况(不同的参数ss和b₁)分析发现：在γ=1+$\sqrt 2 $/2时该方法具有较好的能量耗散特性，能够保证其无条件稳定性；在γ=1-$\sqrt 2 $/2时该方法仅为条件稳定。文献[17]指出，多步长的积分方法会随着系统自由度数量的增加，其稳定性概率大幅提高。文中将该方法求解多自由度问题成功应用，也恰恰证实这一结论。

分析其精度。令单自由度系统的初值条件为：d(t₀)=1和v(t₀)=1。图 9给出了采用该耦合方法得到t=0.5 s的全局误差。从图中不难发现：该耦合方法具有二阶精度。

4 多自由度模型的数值分析

为直观地说明该耦合方法在求解多自由度问题时的算法特性，选取图 10所示的结构模型。考虑到正阻尼对稳定性有利，且导致系统能量降低，为说明算法耗散特性，故假设阻尼为0。结构其他系统参数为：E= 2×10⁸ kN/m²，I=2×10^-5 m⁴，m₁ =1×10⁴ kg，m₂=5×10³ kg，ρ=2，r=2，l=5 m。分离后的结构模型中的质量矩阵和刚度矩阵分别为

$ {\mathit{\boldsymbol{M}}_A} = \frac{r}{{1 + r}}\left[ {\begin{array}{*{20}{c}} {{m_1}}&0\\ 0&{{\rho ^2}{m_1}} \end{array}} \right], $

$ {\mathit{\boldsymbol{M}}_B} = \frac{1}{{1 + r}}\left[ {\begin{array}{*{20}{c}} {{m_1}}&0&0\\ 0&{{\rho ^2}{m_1}}&0\\ 0&0&{{m_2}\left( {1 + r} \right)} \end{array}} \right], $

$ {\mathit{\boldsymbol{K}}_A} = \frac{{EI}}{{l_A^3}}\left[ {\begin{array}{*{20}{c}} {12}&{6l}\\ {6l}&{7{l^2}} \end{array}} \right], $

${\mathit{\boldsymbol{K}}_B} = \frac{{EI}}{{l_B^3}}\left[ {\begin{array}{*{20}{c}} 3&{ - 3l}&{ - 3}\\ { - 3l}&{6{l^2}}&{3l}\\ { - 3}&{3l}&3 \end{array}} \right]{\rm{。}}$

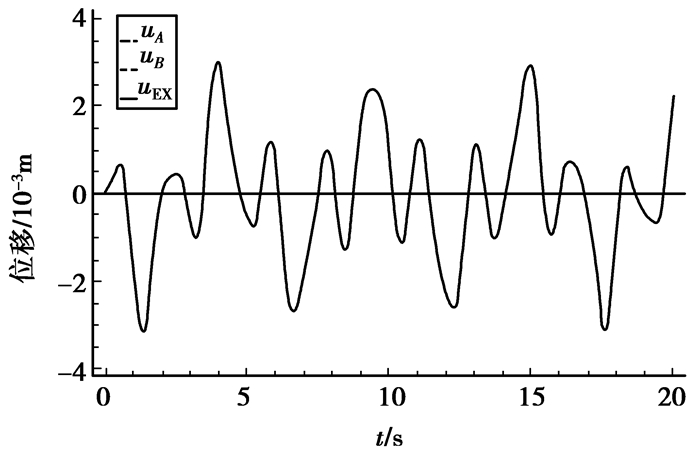
所选用的初值条件为：所有位移取为0；所有平动速度为0.001 m/s；转动速度为0.01 rad/s。数值模拟采用的是自编的Mathematica程序，并选取算法参数γ=1-$\sqrt 2 $/2，ss=10，Δt=10 ms。数值模拟主要针对耦合积分方法的位移偏移，图 10给出了采用该方法求解得到的顶点位移响应。从图 11中可以看出，计算结果与精确解较接近，没有出现明显的能量耗散(energy decay)和周期滞后(period delay)，与收敛性分析的结果一致。较好的精度一方面取决于Rosenbrock方法的特性(如图 3所示)，同时也说明该耦合方法的界面耦联及插值过程中没有引入过多的数值阻尼。

5 结论

直接积分方法，如Newmark系列积分方法和Runge-Kutta法可能不太适合复杂结构或复杂问题的实时子结构试验。众所周知，实时子结构试验需要实时加载，而积分方法很难在控制需要的步长内完成对数值子结构的求解。为此，文中提出了一种具有并行格式的耦合积分方法，并对其稳定性和精度进行了理论分析。然后通过三自由度分离质量模型的模拟，验证了该方法的收敛性和其他算法性能。理论分析和数值模拟结果表明，该方法具有良好的稳定性和二阶精度，与直接积分方法相比更适合用于复杂结构的实时子结构试验及类似的并行模拟。