2. 南京信息工程大学 电子与信息工程学院, 江苏 南京 210044
2. College of Electronic and Information Engineering, Nanjing University of Information Science and Technology, Nanjing 210044, Jiangsu, China
自适应模糊控制作为一种研究非线性控制的有效方法引起了人们的广泛关注.其成功应用在于自适应模糊逻辑系统具有一致逼近的特性,能够在任意精度上逼近一个定义在致密集上的连续非线性函数[1]。在自适应模糊控制中,采用“if-then”规则来构建自适应模糊逻辑系统,用来逼近系统中未知不确定部分.以此为基础设计控制器,当对模型施加恰当的控制,可使系统有期望的输出。文献[2-4]给出了几种单输入单输出和多输入多输出非线性系统的自适应模糊控制方案,所设计的控制器可使非线性系统稳定并使系统输出跟踪期望信号。
在实际工程中存在着许多非线性系统,都不可避免地存在着多种时延因素,比如机械臂系统,由于惯性效应导致连杆之间的时延行为发生,还有电网和核反应堆系统等,时延的存在使得控制器设计不同于对传统非线性控制器设计,从而非线性时延系统的稳定性问题备受关注。文献[5-16]提出了多种行之有效的非线性时延系统的模糊控制方案。这些控制手段不但具有很好的理论突破,而且还成功的应用到工程设计中。文献[5-7]提出了采用时延模糊T-S模型的建模方法。但是该方法忽略了对非线性时延函数的建模误差,可是建模误差的忽略会影响系统的稳定性。文献[8-10]假定非线性时延函数满足匹配条件。尽管匹配条件实现了对误差的建模,然而匹配条件是强假设条件,不易寻求。文献[11-14]考虑建模误差和非线性时延函数有上界。虽然上界比匹配条件降低了保守性,可是上界同样会给控制器的设计增加约束。文献[15-16]提出的模糊自适应方法与反推技术相结合的控制方法。然而反推技术算法复杂,这给控制器的设计增加了难度。
研究工作拓展了文献[2]中的基于T-S模型的自适应模糊系统,推广到时延情形,构建了基于模糊T-S模型的自适应时变时延模糊逻辑系统。用该模糊逻辑系统来逼近未知非线性时变时延函数,从而实现了对一类多输入多输出非线性时变时延系统的建模,以此为基础,提出了一种自适应模糊跟踪控制方案。与文献[5-7]只考虑线性化之后的线性系统相比,笔者没有忽略建模误差,从非线性系统出发设计控制器,从而降低了保守性。与文献[8-14]相比,采用自适应时变时延模糊逻辑系统逼近非线性时延函数,从而克服了对时延函数做匹配条件假设和上界条件假设的不足,同时也降低了不等式的阶数,减少了求解不等式的难度。
具体设计思路:针对一类多输入多输出非线性时变时延系统,构建了基于模糊T-S模型的自适应时变时延模糊逻辑系统用来逼近未知非线性时变时延函数,通过反复调整模糊系统的权值、中心和幅度实现对未知非线性时变时延函数的近似。在自适应算法中,采用跟踪误差来调整自适应时变时延模糊逻辑系统中的参数。应用H∞补偿器来抵消模糊逼近误差和外部扰动。根据Lyapunov稳定性理论,证明了闭环系统的稳定性并满足期望的H∞跟踪性能。机械臂的仿真结果表明了该方案的可行性。
1 问题描述考虑如下多输入多输出非线性时变时延系统
| $ \begin{array}{*{20}{c}} {{{\dot x}_1} = {x_2},}\\ \cdots \\ {{{\dot x}_{\left( {{\beta _1} - 1} \right)}} = {x_{{\beta _1}}},}\\ {{{\dot x}_{{\beta _1}}} = {f_1}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{x}}\left( {t - {\tau _1}\left( t \right), \cdots ,\mathit{\boldsymbol{x}}\left( {t - {\tau _r}\left( t \right)} \right)} \right)} \right. + }\\ {\sum\limits_{i = 1}^m {{g_{1i}}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{x}}\left( {t - {\tau _1}\left( t \right)} \right), \cdots ,\mathit{\boldsymbol{x}}\left( {t - {\tau _r}\left( t \right)} \right)} \right){u_i} + {d_1}} ,} \end{array} $ | (1) |
| $ \begin{array}{*{20}{c}} {{{\dot x}_{\left( {{\beta _1} + 1} \right)}} = {\mathit{\boldsymbol{x}}_{\left( {{\beta _1} + 2} \right)}},}\\ \cdots \\ {{{\dot x}_n} = {f_m}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{x}}\left( {t - {\tau _1}\left( t \right)} \right), \cdots ,\mathit{\boldsymbol{x}}\left( {t - {\tau _r}\left( t \right)} \right)} \right)}\\ {\sum\limits_{i = 1}^m {{g_{mi}}\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{x}}\left( {t - {\tau _1}\left( t \right)} \right), \cdots ,\mathit{\boldsymbol{x}}\left( {t - {\tau _r}\left( t \right)} \right)} \right){u_i} + {d_m}} ,} \end{array} $ |
| $ \begin{array}{*{20}{c}} {{y_1} = {x_1},}\\ \cdots \\ {{y_m} = {x_{\left( {n - {\beta _m} + 1} \right)}},}\\ {x\left( t \right) = \mathit{\Xi }\left( t \right),t \in \left[ { - \zeta ,0} \right],} \end{array} $ |
其中x=[x1, …, x1(β1-1), …, x(n-βm+1), …, x(n-βm+1)(βm-1)]T∈Rn、u=[u1, …, um]T和y=[y1, …, ym]T分别是系统的状态、输入和输出向量,状态是可量测的,β1+β2+…+βm=n,fi、gij(i, j=1, …, m)为充分光滑连续函数,di(i=1, …, m)是外部扰动,Ξ(t)连续,表示系统的初始状态,τi(t)(i=1, 2, …, r)表示时变时延,ζ=max{τi(t)|1≤i≤r}。
引进时延算子σi(t):σi(t)x(t)=x(t-τi(t))(i=0, 1, …, r), 其中τ0(t)=0,τi(t) > 0(i=1, …, r)。令σ(t)=[σ0(t) σ1(t) … σr(t)],于是,含有时变时延的非线性向量函数和含有时变时延非线性矩阵函数可表示为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{F}}_{\sigma \left( t \right)}}\left( x \right) \buildrel \Delta \over = F\left( {x,x\left( {t - {\tau _1}\left( t \right)} \right), \cdots ,x\left( {t - {\tau _r}\left( t \right)} \right)} \right) = }\\ {\left[ {{f_i}\left( {x,x\left( {t - {\tau _1}\left( t \right)} \right), \cdots ,x\left( {t - {\tau _r}\left( t \right)} \right)} \right)} \right],\left( {i = 1,2, \cdots ,m} \right),}\\ {{\mathit{\boldsymbol{G}}_{\sigma \left( t \right)}}\left( x \right) \buildrel \Delta \over = G\left( {x,x\left( {t - {\tau _1}\left( t \right)} \right), \cdots ,x\left( {t - {\tau _r}\left( t \right)} \right)} \right) = }\\ {\left[ {\left( {{g_{ij}}\left( {x,x\left( {t - {\tau _1}\left( t \right)} \right), \cdots ,x\left( {t - {\tau _r}\left( t \right)} \right)} \right)} \right.} \right],}\\ {\left( {i,j = 1,2, \cdots ,m} \right),} \end{array} $ |
其中Fσ(t)(x)是m维的列向量,Gσ(t)(x)是m阶的方矩阵。从而,非线性系统(1)可改写为
| $ \dot x = \mathit{\boldsymbol{A}}x + \mathit{\boldsymbol{B}}\left[ {{\mathit{\boldsymbol{F}}_{\sigma \left( t \right)}}\left( x \right) + {\mathit{\boldsymbol{G}}_{\sigma \left( t \right)}}\left( x \right)u + d} \right], $ | (2) |
| $ \begin{array}{*{20}{c}} {y = \mathit{\boldsymbol{C}}x,}\\ {x = \mathit{\Xi }\left( t \right),t \in \left[ { - \zeta ,0} \right],} \end{array} $ |
式中A=diag[A1, …, Am], B=diag[B1, …, Bm], C=diag[C1, …, Cm],
对给定的参考信号yr1, …, yrm, 定义跟踪误差为e1=yr1-y1, …, em=yrm-ym。令yr=[yr1, …, yrm]T, yr(β)=[yr1(β1), …, yrm(βm)]T, Ym=[y1r, …, y1r(β1-1), …, ymr, …, ymr(βm-1)]T,e=[e1, …, e1(β1-1), …, em, …, em(βm-1)]T。
控制任务:求一个反馈控制u=uσ(t)(x|Θ1, Θ2, α, δ)和调整参数Θ1、Θ2、α和δ的自适应律,使闭环系统满足期望的H∞跟踪性能并使系统输出快速跟踪参考信号。
假定1 ∀x∈U, U是致密集,Gσ(t)(x)是非奇异的。
假定2 τi(t)≤τiM,
自适应模糊逻辑系统(adaptive time-varying delay fuzzy logic systems)具有一致逼近特性,能够在任意精度上逼近一个定义在致密集上的连续非线性函数。构建基于模糊T-S模型的自适应时变时延模糊逻辑系统来逼近m维非线性时变时延向量函数Fσ(t)(x)和m阶非线性时变时延矩阵函数Gσ(t)(x),自适应参数为权值Θ1和Θ2、中心α和幅度δ。对向量函数的第k个分量的逼近形式如下
Rl:若x1是A1l, …, xn是Anl,则
于是, 对向量函数的第k个分量的逼近如下
| $ \begin{array}{*{20}{c}} {{{\hat f}_{k\sigma \left( t \right)}}\left( {x\left| {{\theta _k},\alpha ',\delta '} \right.} \right) = }\\ {\frac{{\sum\limits_{l = 1}^p {\left( {a_0^l + \sum\limits_{i = 1}^n {\left( {a_i^l{x_i} + \sum\limits_{j = 1}^r {a_{ij}^l{x_i}\left( {t - {\tau _j}\left( t \right)} \right)} } \right)} } \right)} \prod\limits_{i = 1}^n {{\mu _{F_i^l}}\left( {{x_i},{{\alpha '}_l},{{\delta '}_l}} \right)} }}{{\sum\limits_{l = 1}^p {\prod\limits_{i = 1}^n {{\mu _{F_i^l}}\left( {{x_i},{{\alpha '}_l},{{\delta '}_l}} \right)} } }} = }\\ {\mathit{\boldsymbol{\xi }}_k^{\rm{T}}\left( {x,\alpha ',\delta '} \right){\theta _k}X,} \end{array} $ | (3) |
式中模糊基函数ξkT(x, α′, δ′)=(ξk1, …, ξkp)∈Rp,
| $ {{\mathit{\boldsymbol{\hat F}}}_{\sigma \left( t \right)}}\left( x \right) = \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\left( {x,\alpha ,\delta } \right){\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1}X,{{\mathit{\boldsymbol{\hat G}}}_{\sigma \left( t \right)}}\left( x \right) = \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\left( {x,\alpha ,\delta } \right){\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2}\bar X, $ | (4) |
式中模糊基函数矩阵Ψ(x, α, δ)=diag[ξ1T(x, α′, δ′), …, ξmT(x, α′, δ′)]∈Rm×pm, 权值Θ1=[θ1T, θ2T, …, θmT]T∈Rpm×(n(r+1)+1),权值Θ2=(θij)m×m∈Rpm×m(n(r+1)+1),中心
定义参数误差
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat F}}}_{\sigma \left( t \right)}}\left( {x\left| {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1},\alpha ,\delta } \right.} \right) - {\mathit{\boldsymbol{F}}_{\sigma \left( t \right)}}\left( x \right) = \left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\left( x \right) - \alpha {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\alpha }\left( x \right) - } \right.}\\ {\left. {\delta {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\delta }\left( x \right)} \right){{\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}}_1}X + \left( {\tilde \alpha {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\alpha }\left( x \right) + \tilde \delta {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\delta }\left( x \right)} \right){\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1}X + {w_1},} \end{array} $ | (5) |
| $ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\hat G}}}_{\sigma \left( t \right)}}\left( {x\left| {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2},\alpha ,\delta } \right.} \right) - {\mathit{\boldsymbol{G}}_{\sigma \left( t \right)}}\left( x \right) = \left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\left( x \right) - \alpha {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\alpha }\left( x \right) - } \right.}\\ {\left. {\delta {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\delta }\left( x \right)} \right){{\mathit{\tilde \Theta }}_2}\bar X + \left( {\tilde \alpha {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\alpha }\left( x \right) + \tilde \delta {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\delta }\left( x \right)} \right){\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2}\bar X + {w_2},} \end{array} $ | (6) |
其中Ψ(x)=Ψ(x, α, δ),Ψα(x)=diag[ξ1α′T(x, α′, δ′), …, ξmα′T(x, α′, δ′)],Ψδ(x)=diag[ξ1δ′T(x, α′, δ′), …, ξmδ′T(x, α′, δ′)],ξiα′T(x, α′, δ′)和ξiδ′T(x, α′, δ′)分别表示ξiT关于α′和δ′的偏导数,w1和w2是残差项。
注1:为了证明所构建的自适应时变时延模糊逻辑系统的一致逼近特性,设Y为由式(3)的模糊逻辑系统组成的集合。可以证明1)(Y,d∞)是一个代数,2)(Y,d∞)能离析U上各点,3)(Y,d∞)在U上任意点上均不为零。根据Stone-Weierstrass定理和1),2),3)可以推出自适应时变时延模糊逻辑系统的泛逼近性。由式(3)可以看出,模糊系统的输出为模糊基函数加权平均与权值的乘积,模糊基函数的中心和幅度也在线调整,从而该模糊系统不但了实现了模糊模型的自动更新,而且能不断修正各隶属度函数,使得模糊逼近更准确,提高了逼近精度。模糊规则通常可选择5-7条,也可适当增加模糊规则数,隶属度函数可选择不对称高斯函数、梯形函数以及钟形函数等。从而自适应模糊逻辑系统的模糊基函数具有更大的可变性和延展性,提高自适应模糊逻辑系统的逼近能力。当逼近误差的范数小于一个数量级10-5时,逼近精度是可接受的,逼近误差可作为程序结束的条件。
3 控制器设计采用模糊控制律
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{u}} = {{\hat G}_{\sigma \left( t \right)}}{{\left( {x\left| {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2},\alpha ,\delta } \right.} \right)}^{ - 1}}\left[ { - {{\hat F}_{\sigma \left( t \right)}}\left( {x\left| {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1},\alpha ,\delta } \right.} \right) + } \right.}\\ {\left. {y_r^{\left( \beta \right)} + {\mathit{\boldsymbol{K}}^{\rm{T}}}e - {u_{com}}} \right],} \end{array} $ | (7) |
式中
因为
| $ \begin{array}{*{20}{c}} {\dot e = \left( {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{K}}^{\rm{T}}}} \right)e + \mathit{\boldsymbol{B}}\left[ {\left( {{{\mathit{\boldsymbol{\hat F}}}_{\sigma \left( t \right)}}\left( {x\left| {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1},\alpha ,\delta } \right.} \right) - {\mathit{\boldsymbol{F}}_{\sigma \left( t \right)}}\left( x \right)} \right) + } \right.}\\ {\left. {\left( {{{\mathit{\boldsymbol{\hat G}}}_{\sigma \left( t \right)}}\left( {x\left| {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2},\alpha ,\delta } \right.} \right) - {\mathit{\boldsymbol{G}}_{\sigma \left( t \right)}}\left( x \right)} \right)u - d} \right] + \mathit{\boldsymbol{B}}{u_{{\rm{com}}}}。} \end{array} $ | (8) |
定义最优参数Θ1*、Θ2*、α*和δ*
| $ \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1^ * \buildrel \Delta \over = \arg \mathop {\min }\limits_{{\mathit{\Theta }_1} \in {\mathit{\Omega }_1}} \left[ {\mathop {\sup }\limits_{x \in U} \left\| {{{\mathit{\boldsymbol{\hat F}}}_{\sigma \left( t \right)}}\left( {x\left| {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1},\alpha ,\delta } \right.} \right) - {\mathit{\boldsymbol{F}}_{\sigma \left( t \right)}}\left( x \right)} \right\|} \right], $ |
| $ \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2^ * \buildrel \Delta \over = \arg \mathop {\min }\limits_{{\mathit{\Theta }_2} \in {\mathit{\Omega }_2}} \left[ {\mathop {\sup }\limits_{x \in U} \left\| {{{\mathit{\boldsymbol{\hat G}}}_{\sigma \left( t \right)}}\left( {x\left| {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2},\alpha ,\delta } \right.} \right) - {\mathit{\boldsymbol{G}}_{\sigma \left( t \right)}}\left( x \right)} \right\|} \right], $ |
| $ \begin{array}{l} {\alpha ^ * } \buildrel \Delta \over = \arg \mathop {\min }\limits_{\alpha \in {\mathit{\Omega }_3}} \left[ {\mathop {\sup }\limits_{x \in U} \left( {\left\| {{{\mathit{\boldsymbol{\hat F}}}_{\sigma \left( t \right)}}\left( {x\left| {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1},\alpha ,\delta } \right.} \right) - {\mathit{\boldsymbol{F}}_{\sigma \left( t \right)}}\left( x \right)} \right\| + } \right.} \right.\\ \left. {\left. {\left\| {{{\mathit{\boldsymbol{\hat G}}}_{\sigma \left( t \right)}}\left( {x\left| {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2},\alpha ,\delta } \right.} \right) - {\mathit{\boldsymbol{G}}_{\sigma \left( t \right)}}\left( x \right)} \right\|} \right)} \right], \end{array} $ |
| $ \begin{array}{l} {\delta ^ * } \buildrel \Delta \over = \arg \mathop {\min }\limits_{\delta \in {\mathit{\Omega }_4}} \left[ {\mathop {\sup }\limits_{x \in U} \left( {\left\| {{{\mathit{\boldsymbol{\hat F}}}_{\sigma \left( t \right)}}\left( {x\left| {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1},\alpha ,\delta } \right.} \right) - {\mathit{\boldsymbol{F}}_{\sigma \left( t \right)}}\left( x \right)} \right\| + } \right.} \right.\\ \left. {\left. {\left\| {{{\mathit{\boldsymbol{\hat G}}}_{\sigma \left( t \right)}}\left( {x\left| {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2},\alpha ,\delta } \right.} \right) - {\mathit{\boldsymbol{G}}_{\sigma \left( t \right)}}\left( x \right)} \right\|} \right)} \right], \end{array} $ |
其中U={x∈Rn},Ω1={Θ1=(θi)m×1∈Rpm×(n(r+1)+1)},Ω2={Θ2=(θij)m×m∈Rpm×m(n(r+1)+1)},Ω3={α=diag[α1, …, αm]∈Rm×pm},Ω4={δ=diag[δ1, …δm]∈Rm×pm}。
于是,定义最优逼近误差为w
| $ \begin{array}{*{20}{c}} {w = \left( {{{\mathit{\boldsymbol{\hat F}}}_{\sigma \left( t \right)}}\left( {x\left| {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1^ * ,{\alpha ^ * },{\delta ^ * }} \right.} \right) - {\mathit{\boldsymbol{F}}_{\sigma \left( t \right)}}\left( x \right)} \right) + }\\ {\left( {{{\mathit{\boldsymbol{\hat G}}}_{\sigma \left( t \right)}}\left( {x\left| {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1^ * ,{\alpha ^ * },{\delta ^ * }} \right.} \right) - {\mathit{\boldsymbol{G}}_{\sigma \left( t \right)}}\left( x \right)} \right)u。} \end{array} $ | (9) |
由式(5)和式(6),改写式(9),从而w=w1+w2u。于是,式(8)可改写为
| $ \begin{array}{*{20}{c}} {\dot e = \left( {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{K}}^{\rm{T}}}} \right)e + \mathit{\boldsymbol{B}}\left[ {\left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\left( x \right) - \alpha {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\alpha }\left( x \right) - } \right.} \right.}\\ {\left. {\left. {\delta {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\delta }\left( x \right)} \right){{\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}}_1}X + \left( {\tilde \alpha {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\alpha }\left( x \right) + \tilde \delta {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\delta }\left( x \right)} \right){\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1}X} \right] + }\\ {\mathit{\boldsymbol{B}}\left[ {\left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\left( x \right) - \alpha {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\alpha }\left( x \right) - \delta {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\delta }\left( x \right)} \right){{\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}}_2}\bar X + \left( {\tilde \alpha {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\alpha }\left( x \right) + } \right.} \right.}\\ {\left. {\tilde \delta {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\delta }\left( x \right){\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2}\bar X} \right]u + \mathit{\boldsymbol{B}}\bar w + \mathit{\boldsymbol{B}}{u_{com}}。} \end{array} $ | (10) |
其中w=w-d。
根据跟踪误差e,选择模糊逻辑系统的参数自适应律
| $ {{\mathit{\boldsymbol{ \boldsymbol{\dot \varTheta} }}}_1} = - {\eta _1}{\left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\left( x \right) - \alpha {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\alpha }\left( x \right) - \delta {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\delta }\left( x \right)} \right)^{\rm{T}}}{\mathit{\boldsymbol{B}}^{\rm{T}}}P\left( {e + 2\mu \dot e} \right){\mathit{\boldsymbol{X}}^{\rm{T}}}, $ | (11) |
| $ {{\mathit{\boldsymbol{ \boldsymbol{\dot \varTheta} }}}_2} = - {\eta _2}{\left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\left( x \right) - \alpha {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\alpha }\left( x \right) - \delta {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\delta }\left( x \right)} \right)^{\rm{T}}}{\mathit{\boldsymbol{B}}^{\rm{T}}}P\left( {e + 2\mu \dot e} \right){\left( {\bar Xu} \right)^{\rm{T}}}, $ | (12) |
| $ \dot \alpha = - {\eta _3}{\mathit{\boldsymbol{B}}^{\rm{T}}}P\left( {e + 2\mu \dot e} \right){\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\alpha }\left( x \right)\left( {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1}X + {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2}\bar Xu} \right)} \right)^{\rm{T}}}, $ | (13) |
| $ \dot \delta = - {\eta _4}{\mathit{\boldsymbol{B}}^{\rm{T}}}P\left( {e + 2\mu \dot e} \right){\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\delta }\left( x \right)\left( {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1}X + {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2}\bar Xu} \right)} \right)^{\rm{T}}}, $ | (14) |
其中η1,η2,η3,η4和μ是正常数,Ψ(x), Ψα(ξ), Ψδ(x)分别为模糊基函数矩阵,模糊基函数矩阵关于中心的偏导数,模糊基函数矩阵关于幅度的偏导数。
采用H∞补偿器ucom来补偿外部扰动和逼近误差,H∞补偿器如下
| $ {u_{com}} = - \left( {\frac{1}{\alpha }} \right){\mathit{\boldsymbol{B}}^{\rm{T}}}Pe, $ | (15) |
其中外部扰动有界,逼近误差的范数小于数量级10-5,对称正定矩阵P由下面不等式给出
| $ \mathit{\boldsymbol{S}} = \left[ {\begin{array}{*{20}{c}} {{s_{11}}}&{{R_{1M}}}& \cdots &{{R_{rM}}}&{\mu \left( {{{\left( {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{K}}^{\rm{T}}}} \right)}^{\rm{T}}} + \frac{1}{\gamma }\mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P}}} \right)}\\ * &{ - \left( {1 - {\tau _{1D}}} \right){R_1} - {R_{1M}}}& \cdots &0&0\\ \vdots&\vdots&\ddots&\vdots&\vdots \\ *&*&\cdots &{ - \left( {1 - {\tau _{rD}}} \right){R_r} - {R_{rM}}}&0\\ *&*&\cdots&* &{ - 2\mu \mathit{\boldsymbol{P}} + \sum\limits_{i = 1}^r {\tau _{iM}^2{\mathit{\boldsymbol{R}}_{iM}}} + \frac{{4{\mu ^2}}}{{{\rho ^2}}}\mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P}}} \end{array}} \right] < 0, $ | (16) |
式中s11=(A-BKT)P+P(A-BKT)-
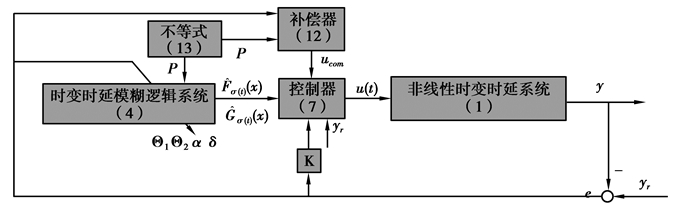
|
图 1 多输入多输出非线性时变时延系统的自适应模糊跟踪控制原理框图 |
定理1 对多输入多输出非线性时变时延系统(1),选择模糊控制律(7),自适应时变时延模糊逻辑系统(4),参数自适应律(11-14),H∞补偿器(15),则闭环系统(8)是有界稳定的并满足H∞跟踪性能
| $ \begin{array}{*{20}{c}} {\int_0^T {{{\mathit{\boldsymbol{\tilde e}}}^{\rm{T}}}\left( { - S} \right)\tilde e{\rm{d}}t} \le {\mathit{\boldsymbol{e}}^{\rm{T}}}\left( 0 \right)Pe\left( 0 \right) + \sum\limits_{i = 1}^r {\int_{ - {\tau _i}\left( 0 \right)}^0 {{\mathit{\boldsymbol{e}}^{\rm{T}}}\left( s \right){R_i}e\left( s \right){\rm{d}}s} } + }\\ {\sum\limits_{i = 1}^r {{\tau _{iM}}\int_{ - {\tau _{iM}}}^0 {\left( {s - {\tau _{iM}}} \right){{\mathit{\boldsymbol{\dot e}}}^{\rm{T}}}\left( s \right){R_{iM}}\dot e\left( s \right){\rm{d}}s} } + }\\ {\frac{1}{{{\eta _1}}}tr\left( {\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}_1^{\rm{T}}\left( 0 \right){{\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}}_1}\left( 0 \right)} \right) + \frac{1}{{{\eta _2}}}tr\left( {\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}_2^{\rm{T}}\left( 0 \right){{\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}}_2}\left( 0 \right)} \right) + }\\ {\frac{1}{{{\eta _3}}}tr\left( {{{\mathit{\boldsymbol{\tilde \alpha }}}^{\rm{T}}}\left( 0 \right)\tilde \alpha \left( 0 \right)} \right) + \frac{1}{{{\eta _4}}}tr\left( {{{\mathit{\boldsymbol{\tilde \delta }}}^{\rm{T}}}\left( 0 \right)\tilde \delta \left( 0 \right)} \right) + {\rho ^2}\int_0^T {\left( {{{\mathit{\boldsymbol{\bar w}}}^{\rm{T}}}\mathit{\boldsymbol{\bar w}}} \right){\rm{d}}t} 。} \end{array} $ | (14) |
其中e=[eT(t) eT(t-τ1(t)) … eT(t-τr(t))
证 选取Lyapunov函数
| $ \begin{array}{*{20}{c}} {V = \frac{1}{2}{\mathit{\boldsymbol{e}}^{\rm{T}}}Pe + \frac{1}{2}\sum\limits_{i = 1}^r {\int_{t - {\tau _i}\left( t \right)}^t {{\mathit{\boldsymbol{e}}^{\rm{T}}}\left( s \right){\mathit{\boldsymbol{R}}_i}e\left( s \right){\rm{d}}s} } + }\\ {\frac{1}{2}\sum\limits_{i = 1}^r {{\tau _{iM}}\int_{t - {\tau _{iM}}}^t {\left( {s - \left( {t - {\tau _{iM}}} \right)} \right){{\mathit{\boldsymbol{\dot e}}}^{\rm{T}}}\left( s \right){\mathit{\boldsymbol{R}}_{iM}}\dot e\left( s \right){\rm{d}}s} } + \frac{1}{{2{\eta _1}}}tr\left( {\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}_1^{\rm{T}}{{\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}}_1}} \right)}\\ { + \frac{1}{{2{\eta _2}}}tr\left( {\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}_2^{\rm{T}}{{\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}}_2}} \right) + \frac{1}{{2{\eta _3}}}tr\left( {{{\tilde \alpha }^{\rm{T}}}\tilde \alpha } \right) + \frac{1}{{2{\eta _4}}}tr\left( {{{\mathit{\boldsymbol{\tilde \delta }}}^{\rm{T}}}\mathit{\boldsymbol{\tilde \delta }}} \right)。} \end{array} $ |
| $ \begin{array}{*{20}{c}} {\dot V = \frac{1}{2}{\mathit{\boldsymbol{e}}^{\rm{T}}}\left[ {{{\left( {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{K}}^{\rm{T}}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{P}} + \mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{K}}^{\rm{T}}}} \right) - \frac{2}{\alpha }\mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P}}} \right]\mathit{\boldsymbol{e + }}}\\ {\frac{1}{2}{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{PB\bar w + }}\frac{1}{2}{{\mathit{\boldsymbol{\bar w}}}^{\rm{T}}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{Pe + }}\frac{1}{2}{\mathit{\boldsymbol{e}}^{\rm{T}}}\sum\limits_{i = 1}^r {{\mathit{\boldsymbol{R}}_i}e} - }\\ {\frac{1}{2}\sum\limits_{i = 1}^r {\left( {1 - {\tau _{iD}}} \right){\mathit{\boldsymbol{e}}^{\rm{T}}}\left( {t - {\tau _i}\left( t \right)} \right){\mathit{\boldsymbol{R}}_i}e\left( {t - {\tau _i}\left( t \right)} \right)} + }\\ {\frac{1}{2}{{\mathit{\boldsymbol{\dot e}}}^{\rm{T}}}\sum\limits_{i = 1}^r {\tau _{iM}^2{\mathit{\boldsymbol{R}}_{iM}}\mathit{\boldsymbol{\dot e}}} - \frac{1}{2}\sum\limits_{i = 1}^r {\left( {{\mathit{\boldsymbol{e}}^{\rm{T}}}\left( t \right) - {\mathit{\boldsymbol{e}}^{\rm{T}}}\left( {t - } \right.} \right.} }\\ {\left. {{\tau _i}\left( t \right)} \right){\mathit{\boldsymbol{R}}_{iM}}\left( {e\left( t \right) - e\left( {t - {\tau _i}\left( t \right)} \right) + \left[ {{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{PB}}\left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\left( x \right) - } \right.} \right.} \right.}\\ {\left. {\left. {\alpha {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\alpha }\left( x \right) - \delta {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\delta }\left( x \right)} \right){{\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}}_1}X + \frac{1}{{{\eta _1}}}tr\left( {\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}_1^{\rm{T}}{{\mathit{\boldsymbol{ \boldsymbol{\dot {\tilde \varTheta}} }}}_1}} \right)} \right] + }\\ {\left[ {{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{PB}}\left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\left( x \right) - \alpha {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\alpha }\left( x \right) - \delta {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\delta }\left( x \right)} \right){{\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}}_2}\bar Xu} \right. + }\\ {\left. {\frac{1}{{{\eta _2}}}tr\left( {\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}_2^{\rm{T}}{{\mathit{\boldsymbol{ \boldsymbol{\dot {\tilde \varTheta}} }}}_2}} \right)} \right] + \left[ {{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{PB}}\tilde \alpha {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\alpha }\left( x \right)\left( {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1}X + {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2}\bar Xu} \right)} \right. + }\\ {\left. {\frac{1}{{{\eta _3}}}tr\left( {{{\mathit{\boldsymbol{\tilde \alpha }}}^{\rm{T}}}\dot {\tilde \alpha} } \right)} \right] + \left[ {{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{PB}}\tilde \delta {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\delta }\left( x \right)\left( {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1}X + {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2}\bar Xu} \right) + \frac{1}{{{\eta _4}}}tr\left( {{{\mathit{\boldsymbol{\tilde \delta }}}^{\rm{T}}}\dot {\tilde \delta} } \right)} \right]。} \end{array} $ | (18) |
对任意的正常数μ > 0,有下面等式(19)和不等式(20)成立
| $ \begin{array}{*{20}{c}} {0 = \frac{1}{2}\left( {2\mu {{\mathit{\boldsymbol{\dot e}}}^{\rm{T}}}P\mathit{\boldsymbol{\dot e}} + \mu {{\mathit{\boldsymbol{\dot e}}}^{\rm{T}}}P\left\{ {\left( {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{K}}^{\rm{T}}}} \right)e + } \right.} \right.}\\ {\mathit{\boldsymbol{B}}\left[ {\left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\left( x \right) - \alpha {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\alpha }\left( x \right) - \delta {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\delta }\left( x \right)} \right){{\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}}_1}X + \left( {\tilde \alpha {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\alpha }\left( x \right) + } \right.} \right.}\\ {\left. {\left. {\tilde \delta {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\delta }\left( x \right)} \right){\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1}X} \right] + \mathit{\boldsymbol{B}}\left[ {\left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\left( x \right) - \alpha {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\alpha }\left( x \right) - } \right.} \right.}\\ {\left. {\left. {\delta {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\delta }\left( x \right)} \right){{\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}}_2}\bar X + \left( {\tilde \alpha {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\alpha }\left( x \right) - \tilde \delta {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\delta }\left( x \right)} \right){\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2}\bar X} \right]u + }\\ {\left. {\mathit{\boldsymbol{B\bar w}} + \mathit{\boldsymbol{B}}{u_{com}}} \right\} + \mu \left\{ {\left( {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{K}}^{\rm{T}}}} \right)e + \mathit{\boldsymbol{B}}\left[ {\left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\left( x \right) - } \right.} \right.} \right.}\\ {\left. {\left. {\alpha {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\alpha }\left( x \right) - \delta {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\delta }\left( x \right)} \right){{\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}}_1}X + \left( {\tilde \alpha {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\alpha }\left( x \right) - \tilde \delta {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\delta }\left( x \right)} \right){\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1}X} \right] + }\\ {\mathit{\boldsymbol{B}}\left[ {\left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\left( x \right) - \alpha {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\alpha }\left( x \right) - \delta {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\delta }\left( x \right)} \right){{\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}}_2}\bar X + \left( {\tilde \alpha {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\alpha }\left( x \right) + } \right.} \right.}\\ {\left. {{{\left. {\left. {\left. {\tilde \delta {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\delta }\left( x \right)} \right){\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2}\bar X} \right]u + \mathit{\boldsymbol{B\bar w}} + \mathit{\boldsymbol{B}}{u_{com}}} \right\}}^{\rm{T}}}P\dot e} \right)。} \end{array} $ | (19) |
| $ \begin{array}{*{20}{c}} {\frac{1}{2}\mu \left( {{{\mathit{\boldsymbol{\dot e}}}^{\rm{T}}}\mathit{\boldsymbol{PB\bar w + }}{{\mathit{\boldsymbol{\bar w}}}^{\rm{T}}}{B^{\rm{T}}}P\mathit{\boldsymbol{\dot e}}} \right) \le }\\ {\frac{1}{2}\left( {\frac{{4{\mu ^2}}}{{{\rho ^2}}}{{\mathit{\boldsymbol{\dot e}}}^{\rm{T}}}\mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{B}}^{\rm{T}}}P\dot e + \frac{{{\rho ^2}}}{4}{{\mathit{\boldsymbol{\bar w}}}^{\rm{T}}}\mathit{\boldsymbol{\bar w}}} \right)。} \end{array} $ | (20) |
又因为
| $ \frac{1}{2}{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{PB\bar w}} + \frac{1}{2}{{\mathit{\boldsymbol{\bar w}}}^{\rm{T}}}{\mathit{\boldsymbol{B}}^{\rm{T}}}Pe \le \frac{1}{2}\left( {\frac{4}{{{\rho ^2}}}{\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{B}}^{\rm{T}}}Pe + \frac{{{\rho ^2}}}{4}{{\mathit{\boldsymbol{\bar w}}}^{\rm{T}}}\mathit{\boldsymbol{\bar w}}} \right)。$ | (21) |
于是,对式(18)左右两端分别加式(19)的左右两端,再由不等式(20)(21),得到
| $ \begin{array}{*{20}{c}} {\dot V \le \frac{1}{2}{\mathit{\boldsymbol{e}}^{\rm{T}}}\left[ {{{\left( {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{K}}^{\rm{T}}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{P}} + \mathit{\boldsymbol{P}}\left( {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{K}}^{\rm{T}}}} \right) - } \right.}\\ {\left. {\frac{2}{\alpha }\mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P + }}\frac{4}{{{\rho ^2}}}\mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P}}} \right]\mathit{\boldsymbol{e + }}\frac{1}{2}\left( {\frac{4}{{{\rho ^2}}}{e^{\rm{T}}}\mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{B}}^{\rm{T}}}Pe + } \right.}\\ {\left. {\frac{{{\rho ^2}}}{4}{{\mathit{\boldsymbol{\bar w}}}^{\rm{T}}}\mathit{\boldsymbol{\bar w}}} \right) + \frac{1}{2}{\mathit{\boldsymbol{e}}^{\rm{T}}}\sum\limits_{i = 1}^r {{R_i}e} - \frac{1}{2}\sum\limits_{i = 1}^r {\left( {1 - {\tau _{iD}}} \right){\mathit{\boldsymbol{e}}^{\rm{T}}}\left( {t - } \right.} }\\ {\left. {{\tau _i}\left( t \right)} \right){\mathit{\boldsymbol{R}}_i}e\left( {t - {\tau _i}\left( t \right)} \right) + \frac{1}{2}{{\dot e}^{\rm{T}}}\sum\limits_{i = 1}^r {\tau _{iM}^2{\mathit{\boldsymbol{R}}_{iM}}\dot e - } }\\ {\frac{1}{2}\sum\limits_{i = 1}^r {\left( {{\mathit{\boldsymbol{e}}^{\rm{T}}}\left( t \right) - {\mathit{\boldsymbol{e}}^{\rm{T}}}\left( {t - {\tau _i}\left( t \right)} \right){\mathit{\boldsymbol{R}}_{iM}}\left( {e\left( t \right) - e\left( {t - {\tau _i}\left( t \right)} \right)} \right.} \right.} + }\\ {\frac{1}{2}\left( {\frac{{4{\mu ^2}}}{{{\rho ^2}}}{{\dot e}^{\rm{T}}}\mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{B}}^{\rm{T}}}P\dot e + \frac{{{\rho ^2}}}{4}{{\mathit{\boldsymbol{\bar w}}}^{\rm{T}}}\mathit{\boldsymbol{\bar w}}} \right) + \frac{1}{2}\left[ {2\mu {{\dot e}^{\rm{T}}}P\dot e + } \right.}\\ {\mu {{\mathit{\boldsymbol{\dot e}}}^{\rm{T}}}P\left( {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{K}}^{\rm{T}}}} \right)e + \mu {\mathit{\boldsymbol{e}}^{\rm{T}}}{{\left( {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{K}}^{\rm{T}}}} \right)}^{\rm{T}}}P\dot e - }\\ {\left. {\left( {\frac{\mu }{\alpha }} \right){{\dot e}^{\rm{T}}}\mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{B}}^{\rm{T}}}Pe - \left( {\frac{\mu }{\alpha }} \right){\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{PB}}{\mathit{\boldsymbol{B}}^{\rm{T}}}P\dot e} \right] + }\\ {\left[ {{{\left( {e + 2\mu \dot e} \right)}^{\rm{T}}}\mathit{\boldsymbol{PB}}\left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\left( x \right) - \alpha {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\alpha }\left( x \right) - } \right.} \right.}\\ {\left. {\left. {\delta {\mathit{\Psi }_\delta }\left( x \right)} \right){{\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}}_1}X + \frac{1}{{{\eta _1}}}tr\left( {\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}_1^{\rm{T}}{{\mathit{\boldsymbol{ \boldsymbol{\dot {\tilde \varTheta}} }}}_1}} \right)} \right] + }\\ {\left[ {{{\left( {e + 2\mu \dot e} \right)}^{\rm{T}}}\mathit{\boldsymbol{PB}}\left( {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}\left( x \right) - \alpha {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\alpha }\left( x \right) - } \right.} \right.}\\ {\left. {\left. {\delta {\mathit{\Psi }_\delta }\left( x \right)} \right){{\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}}_2}X + \frac{1}{{{\eta _2}}}tr\left( {\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}_2^{\rm{T}}{{\mathit{\boldsymbol{ \boldsymbol{\dot {\tilde \varTheta}} }}}_2}} \right)} \right] + }\\ {\left[ {{{\left( {e + 2\mu \dot e} \right)}^{\rm{T}}}\mathit{\boldsymbol{PB}}\tilde \alpha {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\alpha }\left( x \right)\left( {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1}X + {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2}\bar Xu} \right) + } \right.}\\ {\left. {\frac{1}{{{\eta _3}}}tr\left( {{{\mathit{\boldsymbol{\tilde \alpha }}}^{\rm{T}}}\dot {\tilde \alpha} } \right)} \right] + \left[ {{{\left( {e + 2\mu \dot e} \right)}^{\rm{T}}}\mathit{\boldsymbol{PB}}\tilde \delta {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}_\delta }\left( x \right)} \right.}\\ {\left. {\left( {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1}X + {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2}\bar Xu} \right) + \frac{1}{{{\eta _4}}}tr\left( {{{\mathit{\boldsymbol{\tilde \delta }}}^{\rm{T}}}\dot {\tilde \delta} } \right)} \right]。} \end{array} $ | (22) |
令e=[eT(t) eT(t-τ1(t)) … eT(t-τr(t))
| $ \begin{array}{*{20}{c}} {\dot V \le \frac{1}{2}{{\tilde e}^{\rm T}}S\tilde e + \frac{1}{2}{\rho ^2}{{\mathit{\boldsymbol{\bar w}}}^{\rm{T}}}\mathit{\boldsymbol{\bar w}}}\\ { \le - \frac{1}{2}{\lambda _{\min }}\left( { - S} \right){{\left\| {\tilde e} \right\|}^2} + \frac{1}{2}{\rho ^2}{{\left\| {\bar w} \right\|}^2}。} \end{array} $ | (23) |
当‖e‖ >
对式(23)在[0, T]积分,得
| $ \begin{array}{*{20}{c}} {\int_0^{\rm{T}} {{{\mathit{\boldsymbol{\tilde e}}}^{\rm{T}}}\left( { - S} \right)\tilde e{\rm{d}}t} \le {\mathit{\boldsymbol{e}}^{\rm{T}}}\left( 0 \right)Pe\left( 0 \right) + }\\ {\sum\limits_{i = 1}^r {\int_{ - {\tau _i}\left( 0 \right)}^0 {{\mathit{\boldsymbol{e}}^{\rm{T}}}\left( s \right){R_i}e\left( s \right){\rm{d}}s} } + }\\ {\sum\limits_{i = 1}^r {{\tau _{iM}}\int_{ - {\tau _{iM}}}^0 {\left( {s - {\tau _{iM}}} \right){{\mathit{\boldsymbol{\dot e}}}^{\rm{T}}}\left( s \right){\mathit{\boldsymbol{R}}_{iM}}\mathit{\boldsymbol{\dot e}}\left( s \right){\rm{d}}s} } + }\\ {\frac{1}{{{\eta _1}}}tr\left( {\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}_1^{\rm{T}}\left( 0 \right){{\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}}_1}\left( 0 \right)} \right) + \frac{1}{{{\eta _2}}}tr\left( {\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}_2^{\rm{T}}\left( 0 \right){{\mathit{\boldsymbol{ \boldsymbol{\tilde \varTheta} }}}_2}\left( 0 \right)} \right) + }\\ {\frac{1}{{{\eta _3}}}tr\left( {{{\mathit{\boldsymbol{\tilde \alpha }}}^{\rm{T}}}\left( 0 \right)\tilde \alpha \left( 0 \right)} \right) + \frac{1}{{{\eta _4}}}tr\left( {{{\mathit{\boldsymbol{\tilde \delta }}}^{\rm{T}}}\left( 0 \right)\tilde \delta \left( 0 \right)} \right) + {\rho ^2}\int_0^{\rm{T}} {\left( {{{\mathit{\boldsymbol{\bar w}}}^{\rm{T}}}\mathit{\boldsymbol{\bar w}}} \right){\rm{d}}t} 。} \end{array} $ |
证毕。
5 仿真算例设多输入多输出非线性时变时延系统为2连杆机械臂系统[19]
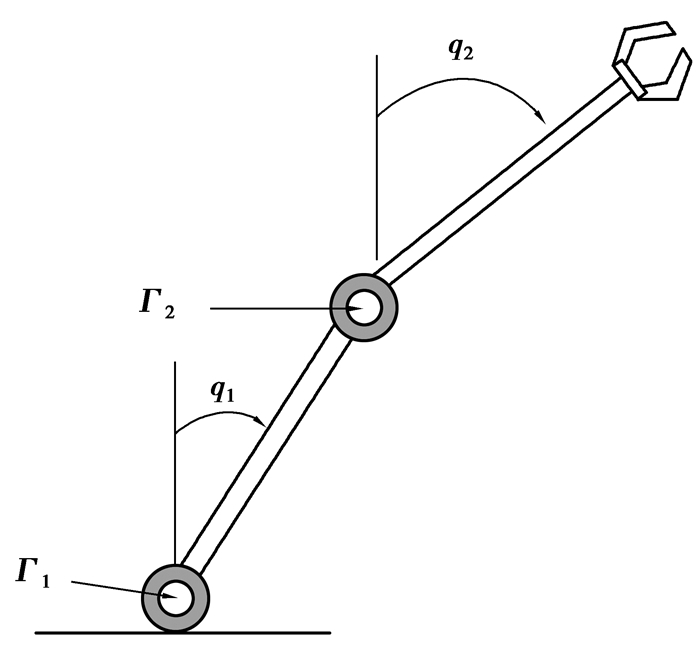
|
图 2 2连杆机械臂系统 |
| $ \begin{array}{*{20}{c}} {\ddot q\left( t \right) + C\left( {q,\dot q} \right)\dot q\left( t \right) + g\left( q \right) = }\\ {B\left( q \right)\mathit{\Gamma }\left( t \right) + \sum\limits_{i = 1}^r {{\xi _i}\left( t \right)q\left( {t - {\tau _i}\left( t \right)} \right) + d'} ,} \end{array} $ |
其中C(q,
令x1=q1, x2=
| $ \begin{array}{*{20}{c}} {\dot x = \mathit{\boldsymbol{A}}x + \mathit{\boldsymbol{B}}\left[ {{\mathit{\boldsymbol{F}}_{\sigma \left( t \right)}}\left( x \right) + {\mathit{\boldsymbol{G}}_{\sigma \left( t \right)}}\left( x \right)u + d'} \right],}\\ {y = Cx,}\\ {x = \mathit{\Xi }\left( t \right),t \in \left[ { - \zeta ,0} \right],} \end{array} $ |
A=diag(A1, A2), B=diag(B1, B2), C=diag(C1, C2), A1=A2=
设计自适应模糊控制器,以跟踪信号yr1与yr2。yr1与yr2满足
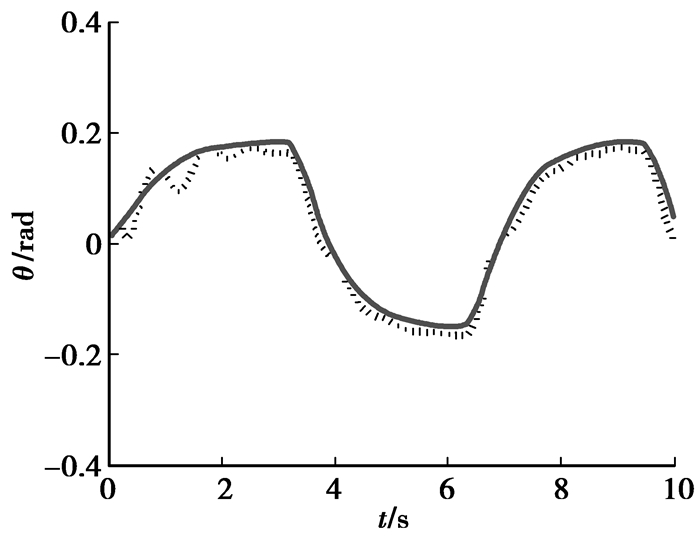
|
图 3 输出y1(虚线)和期望值yr1(实线) |
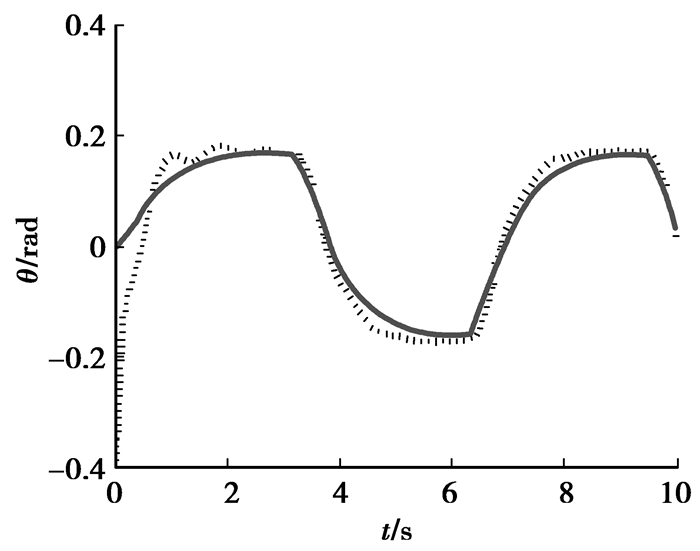
|
图 4 输出y2(虚线)和期望值yr2(实线) |
|
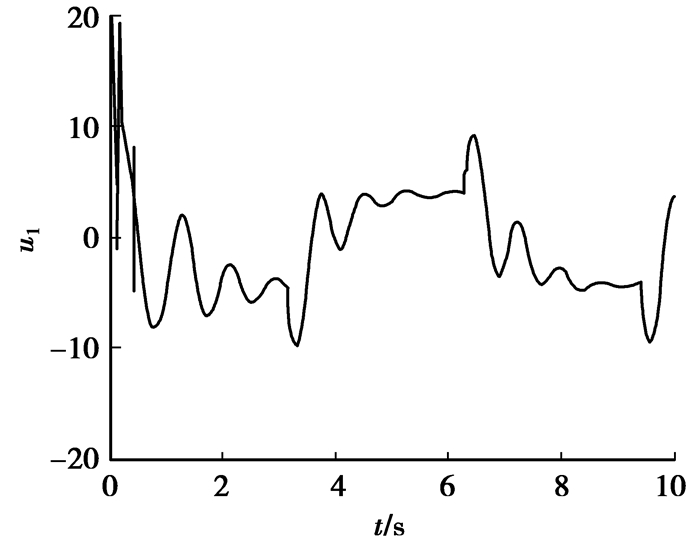
图 5 控制输入u1 |
|
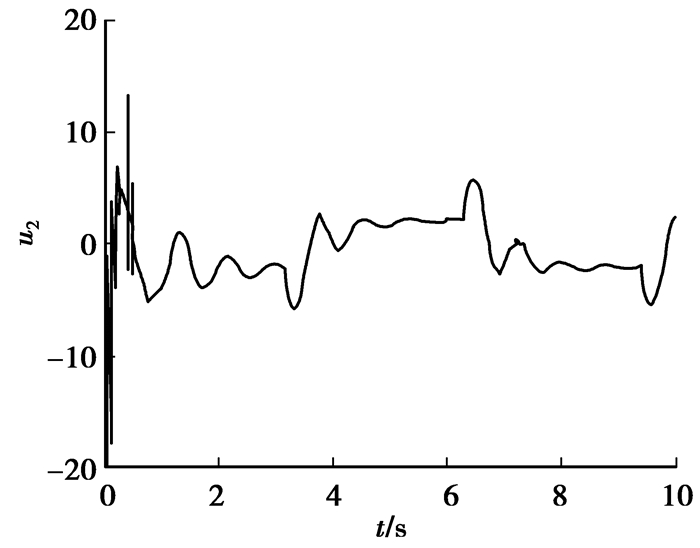
图 6 控制输入u2 |
自适应模糊控制器的具体设计参数如下
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{u}} = {{\mathit{\boldsymbol{\hat G}}}_{\sigma \left( t \right)}}{{\left( {x\left| {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_2},\alpha ,\delta } \right.} \right)}^{ - 1}}\left[ { - {{\mathit{\boldsymbol{\hat F}}}_{\sigma \left( t \right)}}\left( {x\left| {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_1},\alpha ,\delta } \right.} \right) + } \right.}\\ {\left. {y_r^{\left( \beta \right)} + {\mathit{\boldsymbol{K}}^{\rm{T}}}e - {u_{com}}} \right],} \end{array} $ |
式中
选择7条模糊规则, 隶属度函数选择如下
| $ {R^{\left( j \right)}}:{\rm{if}}\;{x_1}\;{\rm{is}}\;F_1^j, \cdots ,{x_4}\;{\rm{is}}\;F_4^j,{\rm{then}}\;y\;{\rm{is}}\;{G^j}\left( {j = 1, \cdots ,7} \right)。$ |
| $ {\mu _{F_i^1}}\left( {{x_i}} \right) = \frac{1}{{1 + \exp \left( {\frac{{{x_i} - {{\alpha '}_1}}}{{{{\delta '}_1}}}} \right)}}, $ |
| $ {\mu _{F_i^2}}\left( {{x_i}} \right) = \exp \left[ { - {{\left( {\frac{{{x_i} - {{\alpha '}_2}}}{{{{\delta '}_2}}}} \right)}^2}} \right], $ |
| $ {\mu _{F_i^3}}\left( {{x_i}} \right) = \exp \left[ { - {{\left( {\frac{{{x_i} - {{\alpha '}_3}}}{{{{\delta '}_3}}}} \right)}^2}} \right], $ |
| $ {\mu _{F_i^4}}\left( {{x_i}} \right) = \exp \left[ { - {{\left( {\frac{{{x_i} - {{\alpha '}_4}}}{{{{\delta '}_4}}}} \right)}^2}} \right], $ |
| $ {\mu _{F_i^5}}\left( {{x_i}} \right) = \exp \left[ { - {{\left( {\frac{{{x_i} - {{\alpha '}_5}}}{{{{\delta '}_5}}}} \right)}^2}} \right], $ |
| $ {\mu _{F_i^6}}\left( {{x_i}} \right) = \exp \left[ { - {{\left( {\frac{{{x_i} - {{\alpha '}_6}}}{{{{\delta '}_6}}}} \right)}^2}} \right], $ |
| $ {\mu _{F_i^7}}\left( {{x_i}} \right) = \frac{1}{{1 + \exp \left( {\frac{{{x_i} - {{\alpha '}_7}}}{{{{\delta '}_7}}}} \right)}}\left( {i = 1,2,3,4} \right)。$ |
令S1=
于是,关于隶属度函数的模糊基矩阵为
Ψ(x)=diag[ξT(x, α′, δ′), ξT(x, α′, δ′)]2×14。
同理可得Ψα(x)=diag[ξα′T(x, α′, δ′), …, ξα′T(x, α′, δ′)]14×14,Ψδ(x)=diag[ξδ′T(x, α′, δ′), …, ξδ′T(x, α′, δ′)]14×14,ξα′T(x, α′, δ′)和ξδ′T(x, α′, δ′)分别表示ξT关于α′和δ′的偏导数, 自适应时变时延模糊逻辑系统中的参数Θ1、Θ2、α和δ的自适应律具有(11-13)的形式,其中η1=1.5,η2=0.8,η3=0.02,η4=0.01是可选择的正常数,Ψ(x),Ψα(x),Ψδ(x)是关于隶属度函数的矩阵, B=diag((0;1), (0;1)), X=diag[X, X],X=(1 x1 x1(t-τ1(t)) x1(t-τ2(t)) … x4 x4(t-τ1(t)) x4(t-τ2(t)))T∈R13,e=[e1,
| $ \mathit{\boldsymbol{P}} = \left[ {\begin{array}{*{20}{c}} {0.0209}&{0.0083}&0&0\\ {0.0083}&{0.0278}&0&0\\ 0&0&{0.0378}&{0.0234}\\ 0&0&{0.0234}&{0.0436} \end{array}} \right]。$ |
当r1(t)和r2(t)均是幅值为1,周期为π的方波信号。可得仿真结果如图 7-图 8所示。
|
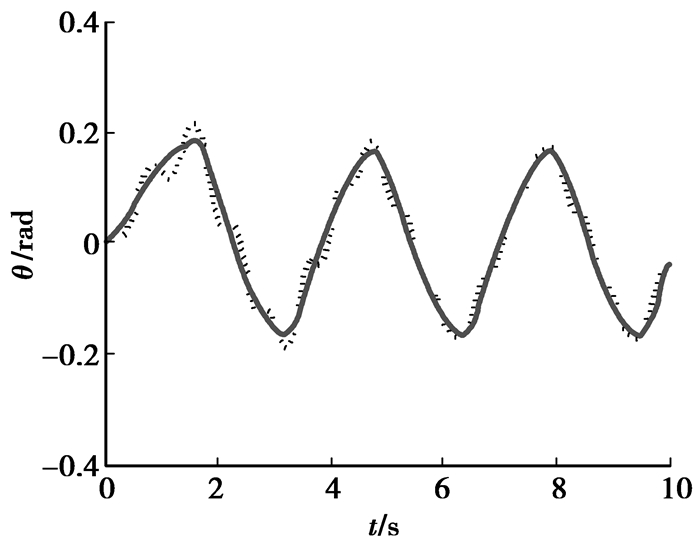
图 7 输出y1(虚线)和期望值yr1(实线) |
|
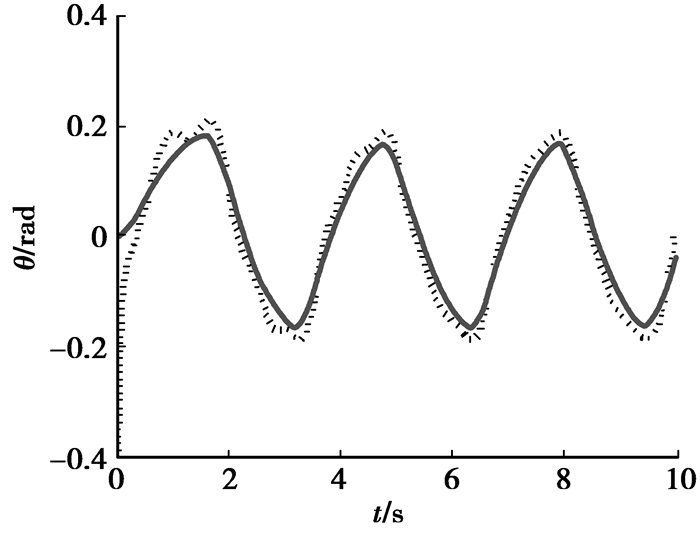
图 8 输出y2(虚线)和期望值yr2(实线) |
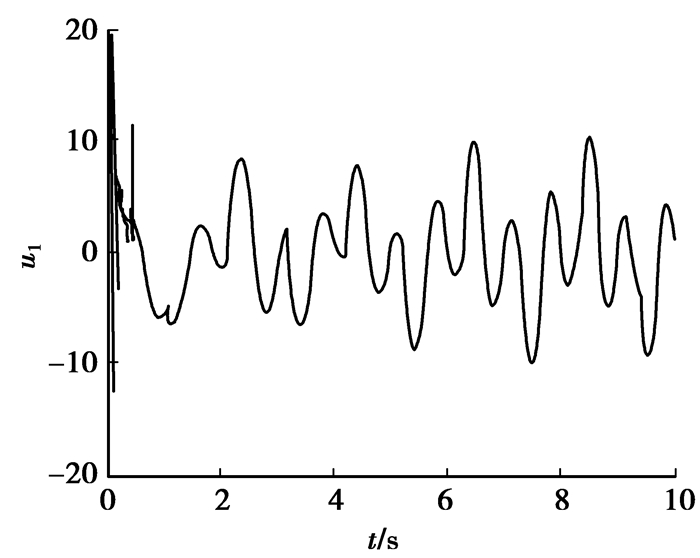
|
图 9 控制输入u1 |
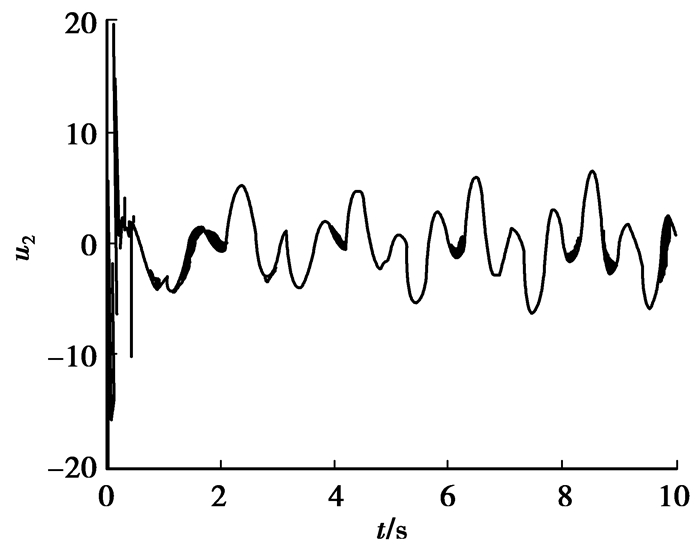
|
图 10 控制输入u2 |
仿真结果表明设计的自适应模糊控制器能快速的跟踪给定的参考信号。
6 结论构建了基于模糊T-S模型的自适应时变时延模糊逻辑系统,通过在线自适应调整模糊系统的参数来逼近未知非线性时变时延函数,从而实现了对多输入多输出非线性时变时延系统的建模,以此为基础设计了模糊控制器,提出了一种自适应模糊跟踪控制方案。该方案从理论分析到仿真结果都表明了该方案的有效性。
| [1] | Wang L X. Stable adaptive fuzzy control of nonlinear systems[C]//Proceedings of the 31st IEEE Decision and Control, December 16-18, 1992, Tucson, AZ. Piscataway:IEEE Press, 1993, 3:2511-2516. |
| [2] | Golea N, Golea A, Benmahammed K. Stable indirect fuzzy adaptive control[J]. Fuzzy Sets and Systems, 2003, 137(3): 353–366. DOI:10.1016/S0165-0114(02)00279-8 |
| [3] | Labiod S, Guerra T M. Adaptive fuzzy control of a class of SISO nonaffine nonlinear systems[J]. Fuzzy Sets and Systems, 2007, 158(10): 1126–1137. DOI:10.1016/j.fss.2006.11.013 |
| [4] | Liu Y J, Tong S C, Wang W. Adaptive fuzzy output tracking control for a class of uncertain nonlinear systems[J]. Fuzzy Sets and Systems, 2009, 160(19): 2727–2754. DOI:10.1016/j.fss.2008.12.016 |
| [5] | Cao Y Y, Frank P M. Stability analysis and synthesis of nonlinear time-delay systems via linear Takagi-Sugeno fuzzy models[J]. Fuzzy Sets and Systems, 2001, 124(2): 213–229. DOI:10.1016/S0165-0114(00)00120-2 |
| [6] | Lin C, Wang Q G, Lee T H. Delay-dependent LMI conditions for stability and stabilization of T-S fuzzy systems with bounded time-delay[J]. Fuzzy Sets and Systems, 2006, 157(9): 1229–1247. DOI:10.1016/j.fss.2005.10.001 |
| [7] | Vasegh N, Majd V J. Fuzzy model-based adaptive synchronization of time-delayed chaotic systems[J]. Chaos, Solitons and Fractals, 2009, 40(3): 1484–1492. DOI:10.1016/j.chaos.2007.09.030 |
| [8] | Guan X P, Chen C L. Delay-dependent guaranteed cost control for T-S fuzzy systems with time delays[J]. IEEE Transactions on Fuzzy Systems, 2004, 12(2): 236–249. DOI:10.1109/TFUZZ.2004.825085 |
| [9] | Tian E, Peng C. Delay-dependent stability analysis and synthesis of uncertain T-S fuzzy systems with time-varying delay[J]. Fuzzy Sets and Systems, 2006, 157(4): 544–559. DOI:10.1016/j.fss.2005.06.022 |
| [10] | Lien C H, Yu K W. Robust control for Takagi-Sugeno fuzzy systems with time-varying state and input delays[J]. Chaos, Solitons & Fractals, 2008, 35(5): 1003–1008. |
| [11] | Lien C H. Stabilization for uncertain Takagi-Sugeno fuzzy systems with time-varying delays and bounded uncertainties[J]. Chaos, Solitons & Fractals, 2007, 32(2): 645–652. |
| [12] | Hua C C, Wang Q G, Guan X P. Robust adaptive controller design for nonlinear time-delay systems via T-S fuzzy approach[J]. IEEE Transactions on Fuzzy Systems, 2009, 17(4): 901–910. DOI:10.1109/TFUZZ.2008.924351 |
| [13] | Hua C C, Wang Q G, Guan X P. Adaptive fuzzy output-feedback controller design for nonlinear time-delay systems with unknown control direction[J]. IEEE Transactions on Systems, Man, and Cybernetics:part B:cybernetics, 2009, 39(2): 363–374. DOI:10.1109/TSMCB.2008.2005204 |
| [14] | Xia Y, Yang Z, Han M. Lag synchronization of unknown chaotic delayed Yang-Yang-type fuzzy neural networks with noise perturbation based on adaptive control and parameter identification[J]. IEEE Transactions on Neural Networks, 2009, 20(7): 1165–1180. DOI:10.1109/TNN.2009.2016842 |
| [15] | Zhang T P, Ge S S. Adaptive neural control of MIMO nonlinear state time-varying delay systems with unknown dead-zones and gain signs[J]. Automatica, 2007, 43(6): 1021–1033. DOI:10.1016/j.automatica.2006.12.014 |
| [16] | Ge S S, Tee K P. Approximation-based control of nonlinear MIMO time-delay systems[J]. Automatica, 2007, 43(1): 31–43. DOI:10.1016/j.automatica.2006.08.003 |
| [17] | Wang M, Chen B, Liu K F, et al. Adaptive fuzzy tracking control of nonlinear time-delay systems with unknown virtual control coefficients[J]. Information Sciences, 2008, 178(22): 4326–4340. DOI:10.1016/j.ins.2008.07.008 |
| [18] | Wang M, Chen B, Liu X P, et al. Adaptive fuzzy tracking control for a class of perturbed strict-feedback nonlinear time-delay systems[J]. Fuzzy Sets and Systems, 2008, 159(8): 949–967. DOI:10.1016/j.fss.2007.12.022 |
| [19] | Yu W S. H∞ tracking-based adaptive fuzzy-neural control for MIMO uncertain robotic systems with time delays[J]. Fuzzy Sets and Systems, 2004, 146(3): 375–401. DOI:10.1016/j.fss.2003.07.001 |
| [20] | Tseng C S, Chen B S, Uang H J. Fuzzy tracking control design for nonlinear dynamic systems via TS fuzzy model[J]. IEEE Transactions on Fuzzy Systems, 2001, 9(3): 381–392. DOI:10.1109/91.928735 |
 2013, Vol. 36
2013, Vol. 36

