2. 东方电气集团东方电机有限公司, 四川 德阳 618000
2. Dongfang Electric Machinery Co. Ltd., Deyang, Sichuan 618000, China
滚动轴承是机械设备中的重要部件之一,但由于磨损、疲劳、腐蚀、过载等因素的影响,滚动轴承容易出现局部损伤故障,特别是在内圈、外圈和滚动体等部位可能出现复合故障。复合故障可能是同时发生的多种故障,也可能是先发生某一故障,导致运转状况的恶化,引起相关部件相继发生故障。在滚动轴承故障发生早期,对复合故障进行准确诊断和预示对于保证机械设备安全可靠运行具有重要的意义。但由于复合故障发生部位不同,对滚动轴承振动影响的方式和程度也有所不同;其次多种故障特征都比较微弱,且叠加在一起会相互干扰,因此给滚动轴承早期复合故障诊断带来很大困难。
目前,关于滚动轴承故障诊断的研究主要集中于单故障诊断,常用的分析方法有频谱分析、包络谱分析、小波分析、经验模态分解(empirical mode decomposition, EMD)、迭代Hilbert变换、局部均值分解等[1-6],其中研究较多的是基于EMD的故障诊断方法。通过将EMD与其他方法相结合,如谱峭度法[7]、奇异值差分谱理论[8]、多尺度形态学[9]等,提出了多种滚动轴承故障诊断方法,较好地解决了滚动轴承单一故障的准确识别。但是,关于滚动轴承复合故障诊断的研究还比较少,主要采用小波变换来实现复合故障特征提取。例如,王晓东等[10]提出了基于自适应多小波的滚动轴承复合故障诊断方法;崔玲丽等[11]采用第二代小波变换和EMD实现轴承损伤性复合故障诊断。这些方法从本质上来讲都是采用二进尺度上的小波变换,存在时频分辨率不高,平移不变性较差,逼近阶次较低等问题,从而会影响多种微弱故障特征的准确提取。通过增加小波基冗余度,可以获得一些人们期望的性质,如对称性、平移不变性、高时频分辨率、高消失矩、高逼近阶次等。常用的冗余小波变换有双密度离散小波变换(Double-density DWT,DD-DWT)[12]和高密度离散小波变换(Higher-density DWT,HD-DWT)[13-14]。与DD-DWT相比,HD-DWT能实现间尺度分析,具有更高的时频栅格采样率和平移不变性,因而更加适合早期复合故障特征提取。
笔者针对现有方法在滚动轴承早期复合故障诊断方面的不足,提出了基于高密度小波单子带重构和包络谱的诊断方法。该方法首先对滚动轴承振动信号进行高密度小波变换,然后对小波系数进行单子带重构以减少频率混叠,再对重构后的信号进行包络谱分析,最后根据特征频率识别滚动轴承出现的各种故障模式。在两个具体实例中的应用结果表明了该方法的有效性和先进性。
1 高密度离散小波变换 1.1 快速分解与重构算法HD-DWT对信号进行分解与重构是通过如图 1所示的3通道滤波器组实现的。图中,hi(n)(i=0, 1, 2)表示小波滤波器;cj(n)和di, j(n)(i=1, 2)分别表示第j级分解后得到的尺度系数和小波系数。由多采样率信号处理的基本关系可知,其理想重建条件为
| $ \begin{array}{*{20}{c}} {{H_0}\left( z \right){H_0}\left( {1/z} \right) + {H_1}\left( z \right){H_1}\left( {1/z} \right) + }\\ {2{H_2}\left( z \right){H_2}\left( {1/z} \right) = 2,} \end{array} $ | (1) |
| $ {H_0}\left( z \right){H_0}\left( { - 1/z} \right) + {H_1}\left( z \right){H_1}\left( { - 1/z} \right) = 0, $ | (2) |
式中Hi(z)表示hi(k)(i=0, 1, 2)的z变换。
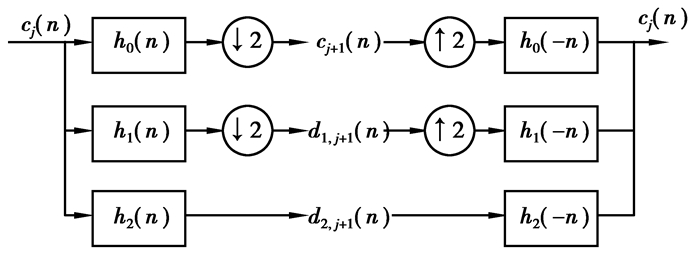
|
图 1 HD-DWT的分解与重构 |
从图 1可知,HD-DWT的快速分解算法可表示为
| $ {c_{j + 1}}\left( n \right) = \sum\limits_k {{h_0}\left( {k - 2n} \right){c_j}\left( k \right)} , $ | (3) |
| $ {d_{1,j + 1}}\left( n \right) = \sum\limits_k {{h_1}\left( {k - 2n} \right){c_j}\left( k \right)} , $ | (4) |
| $ {d_{2,j + 1}}\left( n \right) = \sum\limits_k {{h_2}\left( {k - n} \right){c_j}\left( k \right)} 。$ | (5) |
快速重构算法可表示为
| $\begin{array}{*{20}{l}} {{c_j}\left( n \right) = \sum\limits_k {{h_0}\left( {2k - n} \right){c_{j + 1}}\left( k \right)} + }\\ {\;\;\;\;\;\;\;\;\;\;\;\sum\limits_k {{h_1}\left( {2k - n} \right){d_{1,j + 1}}\left( k \right)} + }\\ {\;\;\;\;\;\;\;\;\;\;\;\sum\limits_k {{h_2}\left( {k - n} \right){d_{2,j + 1}}\left( k \right)} {\rm{。}}} \end{array}$ | (6) |
为了满足理想重建条件式(2),且小波具有指定的K2阶消失矩,则H0(z)和H1(z)可分别取为
| $ {H_0}\left( z \right) = {\left( {\frac{{1 + {z^{ - 1}}}}{2}} \right)^{{K_0}}}A\left( z \right), $ | (7) |
| $ \begin{array}{*{20}{c}} {{H_1}\left( z \right) = {z^{ - \alpha }}{{\left( {\frac{{1 + {z^{ - 1}}}}{2}} \right)}^{{K_1}}}{{\left( {\frac{{1 - {z^{ - 1}}}}{2}} \right)}^{{K_2}}} \cdot }\\ {A\left( { - 1/z} \right){{\left( { - z} \right)}^{ - M}},} \end{array} $ | (8) |
式中:M表示A(z)的次数;α定义为
| $ \alpha = \left\{ \begin{array}{l} 0,M + {K_2}\;为奇数;\\ 1,M + {K_2}\;为偶数。\end{array} \right. $ |
再利用式(1),可得
| $ \begin{array}{l} {H_2}\left( z \right){H_2}\left( {1/z} \right) = \frac{1}{2}\left[ {2 - {H_0}\left( z \right){H_0}\left( {1/z} \right) - } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{H_1}\left( z \right){H_1}\left( {1/z} \right)} \right]。\end{array} $ | (9) |
显然,求出H0(z)和H1(z)后,通过因式分解便能得到H2(z)。特别地,若2-H0(z)H0(1/z)在z=1处具有2K2重零点,则由式(1)可知,H2(z)可表示为
| $ {H_2}\left( z \right) = \frac{1}{{\sqrt 2 }}{\left( {\frac{{1 - {z^{ - 1}}}}{2}} \right)^{{K_2}}}C\left( z \right)。$ | (10) |
于是,由式(7)、(8)和(10)可知,H0(z)、H1(z)和H2(z)分别为低通、带通和高通滤波器。因此,HD-DWT对时频面的采样情况如图 2所示。从图中可见,HD-DWT能实现间尺度分析,因而能更加准确地提取到分布在不同频带中的故障特征。
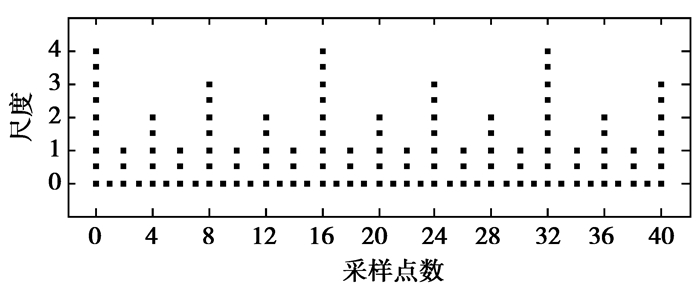
|
图 2 HD-DWT对时频面的采样情况 |
从图 1可见,除第1级高频小波系数d2, 1(n)外,d1, j(n)和d2, j(n)都必须经过下采样才能得到,因而它们都存在频率混叠,这就会影响到复合故障诊断中各个故障特征频率的识别。
下采样后的信号ν(m)和隔点采样前的信号x(m)之间的关系为
| $ v\left( m \right) = x\left( {2m} \right), $ | (11) |
对式(11)两端取傅里叶变换可得
| $ V\left( \omega \right) = \frac{1}{2}\left[ {X\left( {\frac{\omega }{2}} \right) + X\left( {\frac{\omega }{2} + {\rm{ \mathsf{ π} }}} \right)} \right]。$ | (12) |
式(12)说明,下采样产生如下结果:1)采样后信号频谱多出一项X(ω/2+π);2)采样后信号频谱值减半(经重构后频谱值将恢复正常)。可见,下采样会引起严重的频率折叠。另外,下采样还会使数据量减半和时间分辨率降低。而重构过程中的上采样能有效解决这些问题。上采样后的信号w(m)和上采样前的信号v(m)之间的关系为
| $ \left\{ \begin{array}{l} w\left( {2m} \right) = v\left( m \right),\\ w\left( {2m + 1} \right) = 0。\end{array} \right. $ | (13) |
对式(13)两端取傅里叶变换可得
| $ W\left( \omega \right) = V\left( {2\omega } \right)。$ | (14) |
将式(12)代入式(14),并根据X(ω)的周期为2π可得
| $ W\left( \omega \right) = \frac{1}{2}\left[ {X\left( \omega \right) + X\left( {\omega + 2{\rm{ \mathsf{ π} }}} \right)} \right] = X\left( \omega \right)。$ | (15) |
显然,上采样不仅能有效克服频率折叠,还能增大数据量和提高时间分辨率。
于是,笔者提出单子带重构算法来解决HD-DWT快速分解算法中的频率混叠问题。在式(6)中,取cj+1(k)、d1, j+1(k)或d2, j+1(k)为0,并进行迭代操作便形成了单子带重构。对cj+1(n)进行j+1次上采样和低通滤波(滤波器为h0(n))操作后便得到第j+1级分解后的低频尺度系数的重构信号。在式(6)中,令cj+1(k)和d2, j+1(k)为0,得到cj(n),然后对cj(n)进行j次上采样和低通滤波操作后便得到第j+1级分解后中频小波系数d1, j+1(n)的重构信号D1, j+1(n)。同理,可得到第j+1级分解后高频小波系数d2, j+1(n)的重构信号D2, j+1(n)。具体的实现框图如图 3所示。
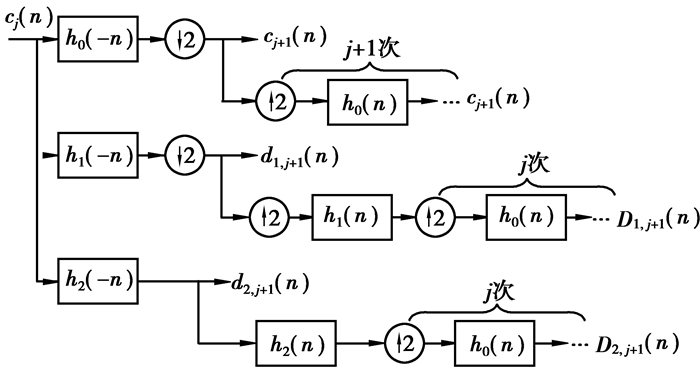
|
图 3 HD-DWT的单子带重构算法 |
显然,任一尺度上的尺度系数和小波系数经过单支重构后,将具有与原信号相同的长度和采样频率。
2 基于HD-DWT和包络谱的复合故障诊断方法利用HD-DWT优良的时频采样特性,并根据滚动轴承故障振动信号具有调制特征,提出了基于HD-DWT和包络谱分析的滚动轴承复合故障诊断方法,其流程如图 4所示。
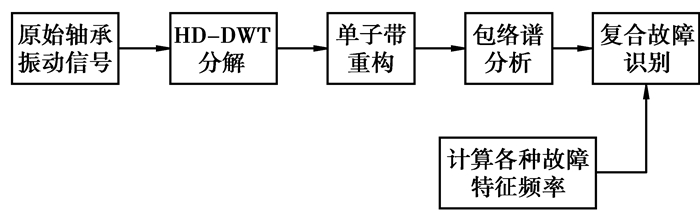
|
图 4 文中所提故障诊断方法流程 |
具体步骤如下:
1) 使具有故障的滚动轴承在一定转速下运转,按一定的采样频率fs获取长度为N的振动信号。
2) 选择具有一定消失矩的高密度小波基,对原始振动信号按图 1进行n级HD-DWT分解。通常情况下,n取2或3即可。
3) 对各级的中频小波系数d1, j(n)和高频小波系数d2, j(n)按图 2进行单子带重构。
4) 对重构后的各子带信号Di, j(n)(i=1, 2)进行Hilbert变换,计算其包络
| $ {A_{i,j}}\left( n \right) = \left| {{\rm{Hilbert}}\left( {{D_{i,j}}\left( n \right)} \right)} \right|, $ | (11) |
式中Hilbert表示对信号进行Hilbert变换。然后对Ai, j(n)进行傅里叶变换得到包络谱。
5) 根据滚动轴承结构尺寸,计算各种典型故障的特征频率,然后通过各子带信号的包络谱识别滚动轴承存在的各种故障。
3 应用实例当滚动轴承发生损伤类故障时,由损伤引起的冲击脉冲力不但会诱发轴承系统的高频固有振动,而且此高频振动的幅值还受到冲击脉冲力的调制。对于这样的高频冲击振动故障信号,包络分析法是一项重要而有效的技术。但是在故障特征比较微弱的情况下,具有故障特征的信号通常会淹没在与转子转速有关的背景信号和其他噪声中,传统的包络分析方法将很难提取到故障特征,因此采用第2节提出的方法来实现滚动轴承早期复合故障诊断。在滚动轴承故障实验台上进行了滚动轴承故障实验。选用的轴承是6205型深沟球轴承,其结构参数如下:内径25 mm,外径52 mm,滚动体个数9,滚动体直径7.938 mm,接触角约为9.509°。实验中采用压电式加速度传感器拾取加速度振动信号,传感器放置在轴承座上。
3.1 具有内圈和外圈故障的滚动轴承复合故障诊断选取具有轻微内圈和外圈故障的6205型轴承进行实验。实验时轴转速为1 796 r/min,采样频率为24 000 Hz,采样点数为19 200。获取的加速度振动信号如图 5所示。按文献[1]中第282页给出的公式,可计算得到此时内圈故障特征频率为162.1 Hz,外圈故障特征频率为107.3 Hz。选用文献[13]中例2所构造的具有3阶消失矩的高密度小波基对图 5所示的信号进行3级分解,再经过单子带重构后,各子带分量的包络谱如图 6所示。从图 6(a)~(c)中可见,在内圈和外圈故障特征频率处均出现了明显的谱线;而从图 6(d)和(e)中可见,在外圈故障特征频率处出现了明显的谱线。因此,可以断定该滚动轴承同时具有内圈和外圈局部故障。需要注意的是,虽然在图 6各个包络谱中还出现了转频和其倍频以及其他一些干扰频率成分,但并不影响内圈和外圈复合故障的识别。
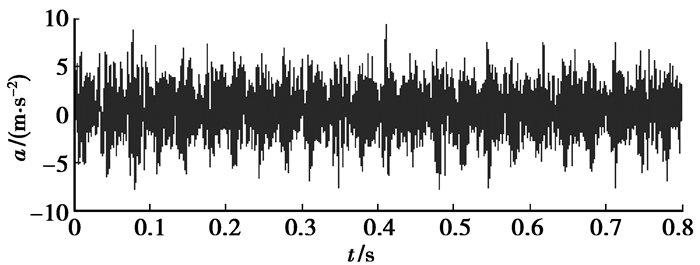
|
图 5 具有内圈和外圈故障的滚动轴承振动信号 |
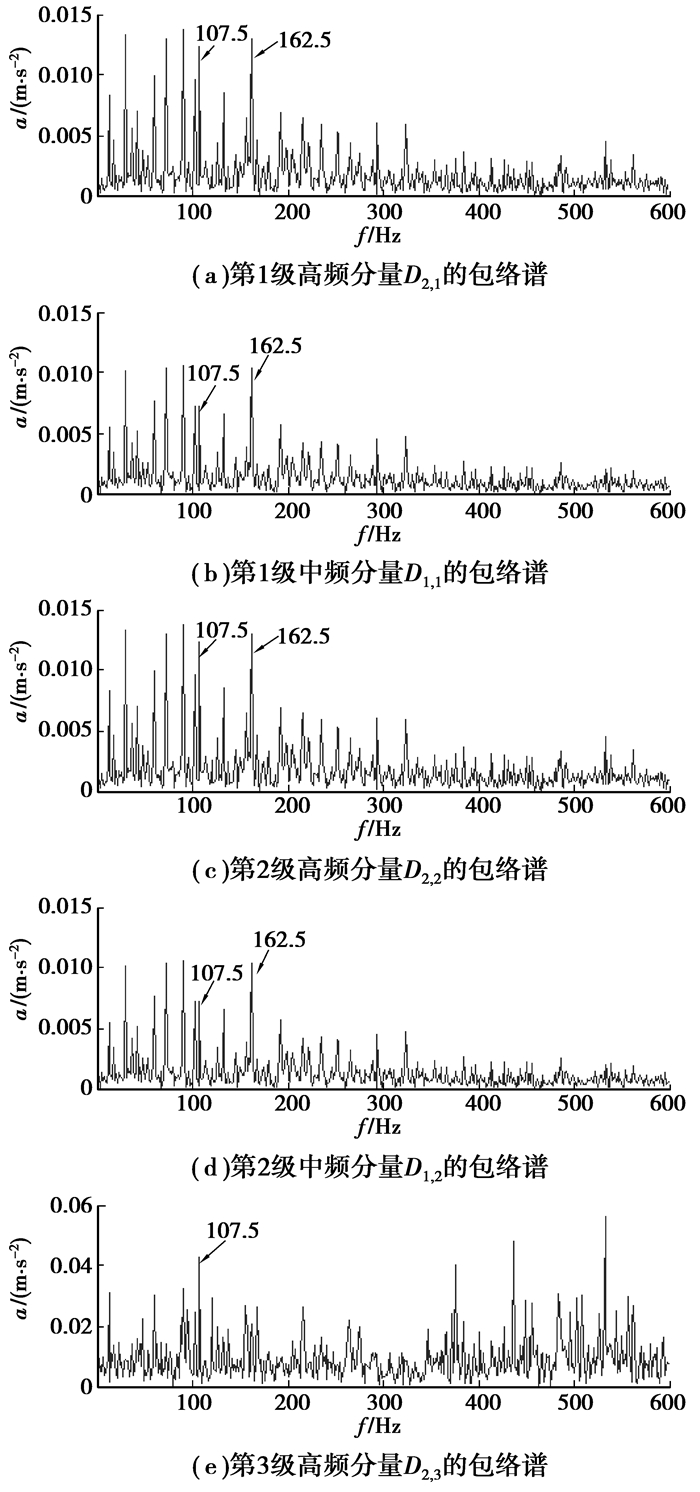
|
图 6 图 5所示信号各子带分量的包络谱 |
为了突出所提方法在滚动轴承早期复合故障诊断中的优势,与直接包络谱、基于DWT的包络谱、基于EMD的包络谱等3种典型方法进行对比。对图 5所示信号直接进行包络谱分析所得结果如图 7所示;用3阶Daubechies小波对图 5所示信号进行1次分解后,再对高频小波系数进行包络谱分析,所得结果如图 8所示;对图 5所示信号进行EMD分解后,得到11个IMF分量,分别对前4个IMF进行包络谱分析,所得结果如图 9(a)~(d)所示。从图 7~9中可见,虽然在内圈和外圈故障特征频率处有谱线,但幅值相对较小;而在图 7和9中甚至看不到反映内圈或外圈故障的特征频率。另外,在其他7个IMF分量的包络谱中,内圈和外圈故障特征频率处也未见明显谱线。显然,与这些方法相比,笔者所提方法能够非常准确地从振动信号中提取到该轴承内圈和外圈的微弱故障特征。
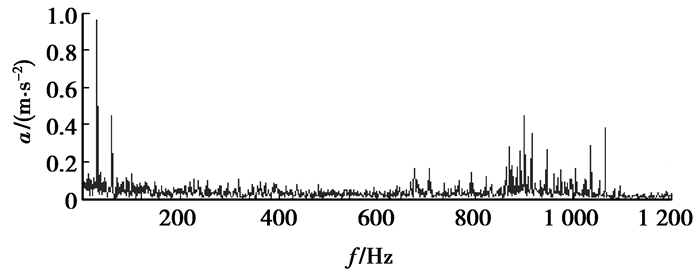
|
图 7 图 5所示信号的直接包络谱 |
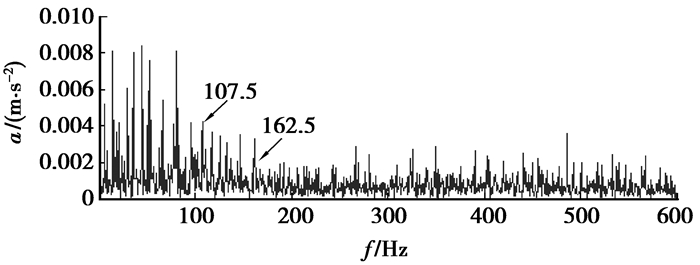
|
图 8 基于DWT的图 5所示信号第1级小波系数的包络谱 |
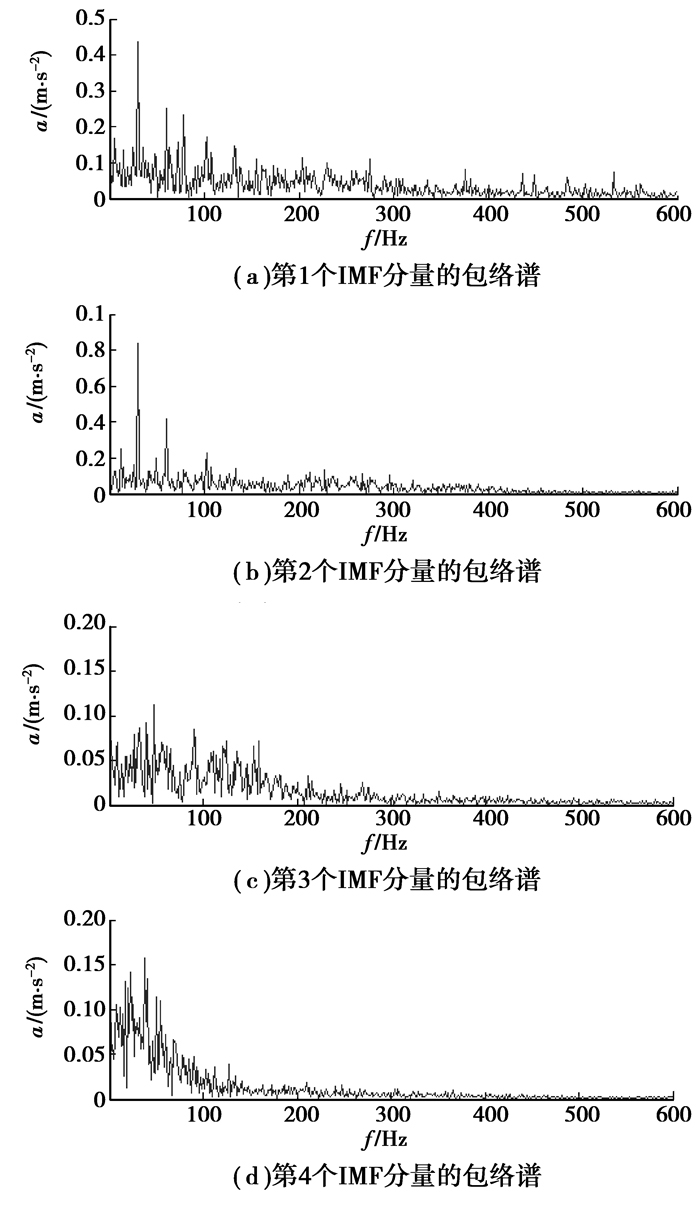
|
图 9 基于EMD的图 5所示信号前4个IMF分量的包络谱 |
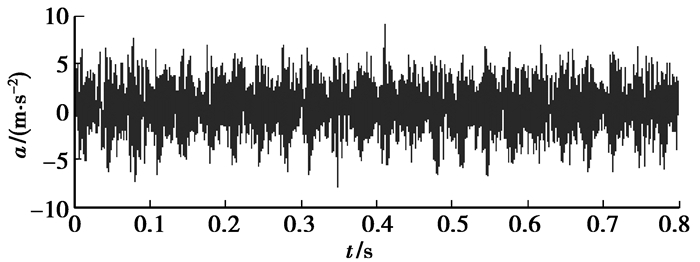
再选取具有轻微滚动体和内圈故障的6205型轴承进行实验。实验时轴转速、采样频率和采样点数均与3.1节保持一致。获取的加速度振动信号如图 10所示。同理,通过计算可得滚动体故障特征频率为139.3 Hz,内圈故障特征频率为162.1 Hz。用具有3阶消失矩的高密度小波基对图 10所示的信号进行2级分解,再经过单子带重构后,各子带分量的包络谱如图 11所示。从图 11(a)~(d)中可见,虽然在转频和其倍频以及其他一些干扰频率处出现了幅值较大的谱线,但在滚动体和内圈故障特征频率处均出现了明显的谱线。因此,可以断定该滚动轴承同时具有滚动体和内圈局部故障。
|
图 10 具有滚动体和内圈故障的滚动轴承振动信号 |

|
图 11 图 10所示信号各子带分量的包络谱 |
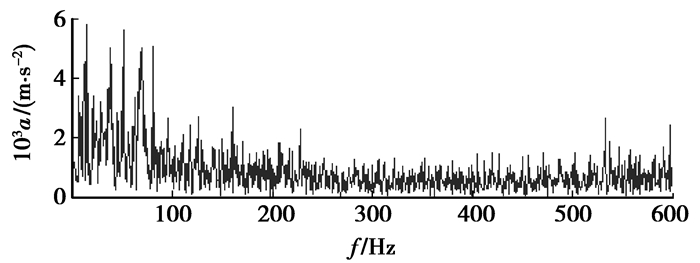
为了进一步表明所提基于HD-DWT和包络谱的滚动轴承复合故障诊断方法的有效性和先进性,利用直接包络谱、基于DWT的包络谱、基于EMD的包络谱等3种典型方法对该信号进行了故障特征提取。对图 10所示信号直接进行包络谱分析所得结果如图 12所示;用3阶Daubechies小波对图 10所示信号进行1次分解后,再对高频小波系数进行包络谱分析,所得结果如图 13所示;对图 10所示信号进行EMD分解后,得到11个IMF分量,分别对前4个IMF进行包络谱分析,所得结果如图 14(a)~(d)所示。从图 12~14中可见,在滚动体和内圈故障特征频率处均未出现谱线峰值。另外,在其他7个分量的包络谱中,滚动体和内圈故障特征频率处均未出现明显谱线,因而无法判断轴承是否发生了故障。这就进一步说明了所提方法比其他方法更能准确地诊断出滚动轴承存在的早期复合故障。

|
图 12 图 10所示信号的直接包络谱 |
|
图 13 基于DWT的图 10所示信号第1级小波系数的包络谱 |
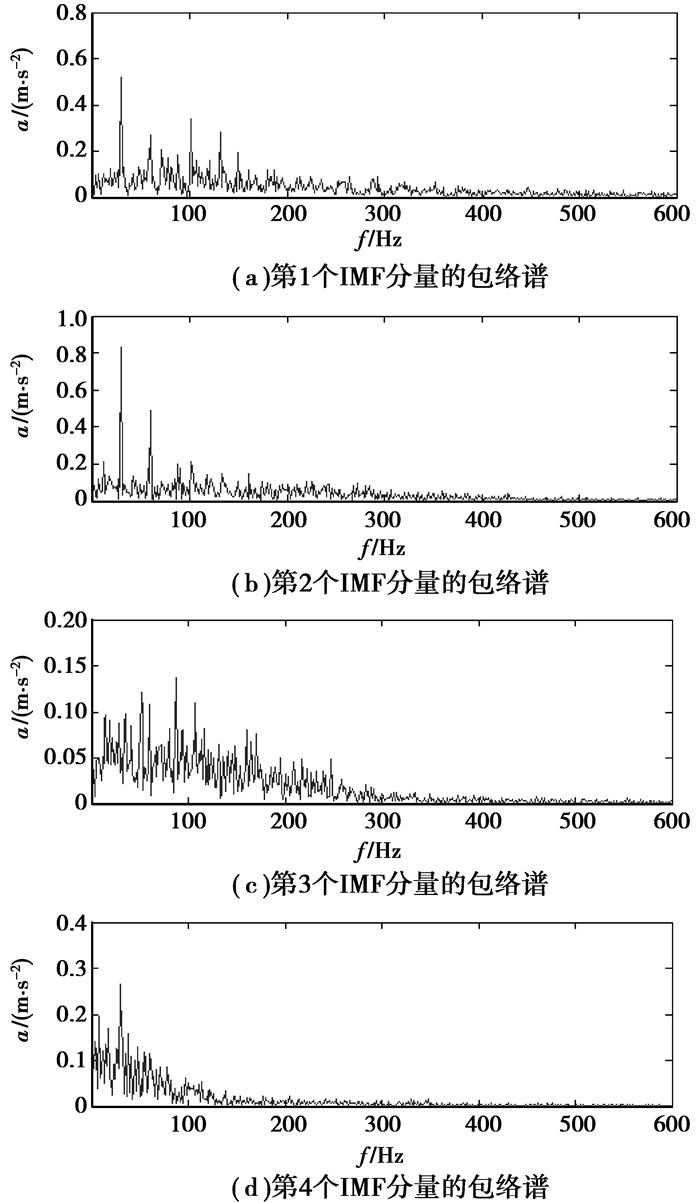
|
图 14 基于EMD的图 10所示信号前4个IMF分量的包络谱 |
HD-DWT与传统的离散小波变换相比,能形成间尺度分析,具有高时频分辨率、近似平移不变性等优点,因而非常适合于滚动轴承早期复合故障特征提取。笔者针对通过HD-DWT获得的小波系数存在频率混叠的问题,提出了HD-DWT的单子带重构算法,得到与原信号具有相同采样频率和长度的各子带分量。然后,对各子带分量进行包络谱分析,根据滚动轴承典型故障特征频率便能实现多种早期故障的准确诊断。将所提方法应用于两个滚动轴承的早期复合故障诊断,并与其他典型方法进行了对比,结果表明了基于HD-DWT和包络谱的复合故障诊断方法的有效性和先进性。
笔者只采用了具有3阶消失矩的最短长度高密度小波基来进行实验,还可以采用其他对称性更好的小波基来实现信号分解,如具有对称低通和带通滤波器的高密度小波基,有望进一步提高滚动轴承复合故障诊断的精度。
| [1] | 沈庆根, 郑水英. 设备故障诊断[M]. 北京: 化学工业出版社, 2006. |
| [2] | Peng Z K, Chu F L. Application of the wavelet transform in machine condition monitoring and fault diagnostics:a review with bibliography[J]. Mechanical Systems and Signal Processing, 2004, 18(2): 199–221. DOI:10.1016/S0888-3270(03)00075-X |
| [3] | Yu D J, Cheng J S, Yang Y. Application of EMD method and Hilbert spectrum to the fault diagnosis of roller bearings[J]. Mechanical Systems and Signal Processing, 2005, 19(2): 259–270. DOI:10.1016/S0888-3270(03)00099-2 |
| [4] | Qin Y, Qin S R, Mao Y F. Research on iterated Hilbert transform and its application in mechanical fault diagnosis[J]. Mechanical Systems and Signal Processing, 2008, 22(8): 1967–1980. DOI:10.1016/j.ymssp.2008.01.014 |
| [5] | Cheng J S, Yang Y, Yang Y. A rotating machinery fault diagnosis method based on local mean decomposition[J]. Digital Signal Processing, 2012, 22(2): 356–366. DOI:10.1016/j.dsp.2011.09.008 |
| [6] |
李锋, 汤宝平, 刘文艺.
遗传算法优化最小二乘支持向量机的故障诊断[J]. 重庆大学学报, 2010, 33(12): 14–20.
LI Feng, TANG Baoping, LIU Wenyi. Fault diagnosis based on least square support vector machine optimized by genetic algorithm[J]. Journal of Chongqing University, 2010, 33(12): 14–20. DOI:10.11835/j.issn.1000-582X.2010.12.003 (in Chinese) |
| [7] |
苏文胜, 王奉涛, 张志新, 等.
EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用[J]. 振动与冲击, 2010, 29(3): 18–21.
SU Wensheng, WANG Fengtao, ZHANG Zhixin, et al. Application of EMD denoising and spectral kurtosis in early fault diagnosis of rolling element bearings[J]. Journal of Vibration and Shock, 2010, 29(3): 18–21. (in Chinese) |
| [8] |
张超, 陈建军, 徐亚兰.
基于EMD分解和奇异值差分谱理论的轴承故障诊断方法[J]. 振动工程学报, 2011, 24(5): 539–545.
ZHANG Chao, CHEN Jianjun, XU Yalan. A bearing fault diagnosis method based on EMD and difference spectrum theory of singular value[J]. Journal of Vibration Engineering, 2011, 24(5): 539–545. (in Chinese) |
| [9] |
罗洁思, 于德介, 彭富强.
基于EMD的多尺度形态学解调方法及其在机械故障诊断中的应用[J]. 振动与冲击, 2009, 28(11): 84–86.
LUO Jiesi, YU Dejie, PENG Fuqiang. Application of multiscale morphology demodulation approach based on EMD in machinery fault diagnosis[J]. Journal of Vibration and Shock, 2009, 28(11): 84–86. (in Chinese) |
| [10] |
王晓冬, 何正嘉, 訾艳阳.
多小波自适应构造方法及滚动轴承复合故障诊断研究[J]. 振动工程学报, 2010, 23(4): 438–444.
WANG Xiaodong, HE Zhengjia, ZI Yanyang. Adaptive construction of multiwavelet and research on composite fault diagnosis of rolling bearing[J]. Journal of Vibration Engineering, 2010, 23(4): 438–444. (in Chinese) |
| [11] |
崔玲丽, 高立新, 殷海晨, 等.
基于第二代小波的复合故障诊断方法研究[J]. 中国机械工程, 2009, 10(4): 442–446.
CUI Lingli, GAO Lixin, YIN Haichen, et al. Research on composite fault diagnosis method based on the second generation wavelet[J]. China Mechanical Engineering, 2009, 10(4): 442–446. (in Chinese) |
| [12] | Selesnick I W. The double-density discrete wavelet transform[M]//Petrosian A, Meyer F G. Wavelets in signal and image analysis:from theory to practice, Dordrecht:Kluwer, 2001. |
| [13] | Selesnick I W. A higher density discrete wavelet transform[J]. IEEE Transactions on Signal Processing, 2006, 54(8): 3039–3048. DOI:10.1109/TSP.2006.875388 |
| [14] | Qin Y, Wang J X, Tang B P, et al. Higher density wavelet frames with symmetric low-pass and band-pass filters[J]. Signal Processing, 2010, 90(12): 3219–3231. DOI:10.1016/j.sigpro.2010.05.027 |
 2013, Vol. 36
2013, Vol. 36


