随着计算机技术、传感器技术及控制技术等的发展,移动机器人在工业、农业、医药及社会服务业领域的应用不断扩大,应用的复杂程度也越来越高[1]。目前对移动机器人的研究大多仍以二自由度移动机器人为主,不能满足特殊情况下的应用,所以目前国内外很多研究人员正在研究全方位移动机器人,如Mecanum轮式结构等全方位移动机器人[2-4]。然而,全方位移动机器人仍未投入到广泛使用,原因在于设计加工过于复杂,行走过程中产生颠簸振动现象且机器人结构和控制复杂,实用性不强[5-6]。笔者提出了一种新型全方位移动机器人,具有极大的柔性,它能更灵活地实现移动机器人的原地打转、侧移及直角转弯等功能。
对该移动机器人的轨迹跟随控制实际上是对参考点的控制,在以往的研究中,大多选取机器人中心进行单点控制[5-7],但本文中的移动机器人由于其结构的复杂性,如仍选用单参考点控制,将会是一个高度耦合的复杂系统,会非常困难,所以,提出一种新型的双参考点控制方法,对每个参考点设计模糊控制器[8-10],有效地实现了移动机器人的路径跟随。
1 移动机器人的结构及运动模型四轮差动全方位移动机器人是由4个驱动轮和4个万向轮组成,4个驱动轮组成两个驱动单元,前驱和后驱,4个万向轮是从动轮,起辅助支撑的作用,如图 1所示。

|
图 1 移动机器人各轮分布图 |
|
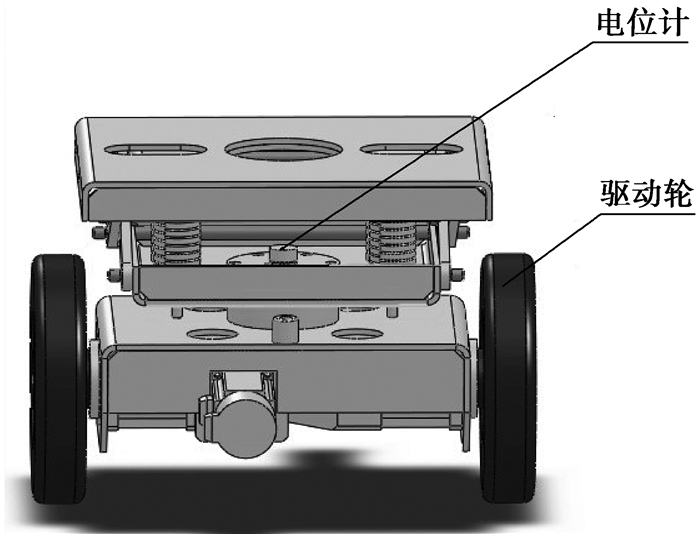
图 2 差速驱动单元 |
驱动单元如图 2所示,两个驱动单元都能通过两个轮的差速调节分别绕各自的中心行走和自由转动,驱动单元上安装有电位计,能够实时测量驱动单元当前转过的角度,即,每个驱动单元等价于在驱动单元中心安装了一个兼有行走和转向功能的驱动轮,但同时又有差速的功能,通过各个驱动电机的不同速度组合,可以得到小车的不同的运动方式。
建立两个坐标系,XOY为小车行走区域的全局固定坐标系,X′O′Y′为基于小车中心的移动坐标系,小车当前位姿是由小车中心在全局坐标中的位置(X, Y)及前进方向与全局坐标X轴正方向的夹角θ确定的,即PO=[X, Y, θ]T。
四轮差动全方位移动机器人的运动学模型如图 3所示。

|
图 3 移动机器人运动模型 |
根据运动学建模,得机器人的运动状态方程为
| $ \begin{array}{l} \frac{1}{2}\left( {\begin{array}{*{20}{c}} {\cos \left( {\theta + {\alpha _1}} \right)}&{\cos \left( {\theta + {\alpha _1}} \right)}&0&0\\ {\sin \left( {\theta + {\alpha _1}} \right)}&{\sin \left( {\theta + {\alpha _1}} \right)}&0&0\\ 0&0&{\cos \left( {\theta + {\alpha _2}} \right)}&{\cos \left( {\theta + {\alpha _2}} \right)}\\ 0&0&{\sin \left( {\theta + {\alpha _2}} \right)}&{\sin \left( {\theta + {\alpha _2}} \right)} \end{array}} \right).\\ \left( {\begin{array}{*{20}{c}} {{\upsilon _1}}\\ {{\upsilon _2}}\\ {{\upsilon _3}}\\ {{\upsilon _4}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1&0&{ - L\;\sin \;\theta }\\ 0&1&{\;\;L\;\cos \;\theta }\\ 1&0&{\;\;L\;\sin \;\theta }\\ 0&1&{ - L\;\cos \;\theta } \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\dot x}\\ {\dot y}\\ {\dot \theta } \end{array}} \right), \end{array} $ | (1) |
式中:L为驱动单元中心到AGV的几何中心距离;B为车轮中心到驱动单元中心的距离;α1、α2为两驱动单元与移动坐标系X′轴夹角,逆时针为正,顺时针为负;v1、v2、v3、v4分别为4个驱动轮的线速度;v1、v2、v3、v4与驱动单元中心o1、o2点的速度及角速度有如下关系:
| $ \left( {\begin{array}{*{20}{c}} {{\upsilon _1}}\\ {{\upsilon _2}}\\ {{\upsilon _3}}\\ {{\upsilon _4}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1&B&0&0\\ 1&{ - B}&0&0\\ 0&0&1&B\\ 0&0&1&{ - B} \end{array}} \right) \cdot \left( {\begin{array}{*{20}{c}} {{\upsilon _{o_1}}}\\ {{\omega _{o_1}}}\\ {{\upsilon _{o_2}}}\\ {{\omega _{o_2}}} \end{array}} \right), $ | (2) |
式中:vo1、vo2分别为两驱动单元中心的线速度;ωo1、ωo2分别为两驱动单元中心的角速度。
2 路径跟随控制器设计路径跟随控制就是设计一种控制律使移动机器人沿临时规划路径运动到期望路径上。由图 3的运动学模型可知,对两驱动单元中心的速度和角速度的控制即可实现对移动机器人位姿的控制。为此,提出一种新型的双点路径跟随方法,通过选取前驱动单元中心为主参考点,后驱动单元中心为从参考点,再采用模糊控制技术分别对两参考点进行角速度及速度模糊控制器的设计。控制框图如图 4所示。

|
图 4 系统控制框图 |
主控制器实现对主参考点的控制,以前驱单元的速度和角速度为输出;主从单元是主、从控制器之间的桥梁,确保从参考点跟随主参考点运动,所以后驱动单元只有角速度控制,其速度是根据主参考点解算得到;从控制器是对从参考点进行控制,以后驱单元的速度和角速度为输出。模糊控制器实现控制要经过模糊化、建立模糊控制规则、模糊推理及清晰化处理等几个步骤[11-12]。
2.1 角速度模糊控制器机器人角速度的大小分别受横向距离误差和方向角度误差的影响,当方向角误差大时,增加角速度大小,反之则减小角速度大小;当横向距离误差大时,增加角速度大小,反之减小角速度大小。所以,角速度控制器以横向距离偏差Ey和角度偏差Ea为输入,以角速度ω为输出,是一个双输入单输出的模糊控制器,其控制结构图见图 5。

|
图 5 角速度模糊控制的结构图 |
选择输入、输出的模糊子集均为{NB(负大),NM(负中),NS(负小),O(零),PS(正小),PM(正中),PB(正大)},且论域均为[-6, +6]。通过调整合适的比例因子ky、ka、kω分别将Ey、Ea、ω这3个变量映射到论域范围。隶属函数选取表达式和运算较为简单的三角形隶属函数,具有灵敏性较高的优点。
其IF-THEN控制规则为IF Ey=A and Ea=B THEN ω=C。
根据模糊控制规则,采用Mamdani方法进行近似模糊推理,设已知输入的模糊量为:x为A′且y是B′,则输出模糊量C′为[13]
| $ \mathit{\boldsymbol{D = A}} \times \mathit{\boldsymbol{B}}:\mu \mathit{\boldsymbol{D}}\left( {{E_y},{E_a}} \right) = \mu \mathit{\boldsymbol{A}}\left( {{E_y}} \right)\Lambda \mu \mathit{\boldsymbol{B}}\left( {{E_a}} \right)。$ |
然后将D改写成向量DT,变两输入为一个新的输入:
| $ {\mathit{\boldsymbol{D}}^{\rm{T}}} = \left[ {{d_{11}},{d_{12}}, \cdots {d_{1n}},{d_{21}},{d_{22}}, \cdots {d_{2n}}, \cdots {d_{m1}},{d_{m2}}, \cdots {d_{mn}}} \right]。$ |
求出关系矩阵:
| $ \begin{array}{l} \mathit{\boldsymbol{R}} = {\mathit{\boldsymbol{D}}^{\rm{T}}} \times \mathit{\boldsymbol{C}}:\mu \mathit{\boldsymbol{R}}\left( {{E_y},{E_a},\omega } \right) = \\ \;\;\;\;\;\;\mu \mathit{\boldsymbol{A}}\left( {{E_y}} \right)\Lambda \mu \mathit{\boldsymbol{B}}\left( {{E_a}} \right)\Lambda \mu \mathit{\boldsymbol{C}}\left( \omega \right), \end{array} $ | (3) |
按上述过程同样求得D′T,最后合成求得
根据人驾驶汽车的操作经验,总结出表 1所示的49条模糊控制规则。
| 表 1 角速度控制器规则表 |
传统的机器人路径跟随为匀速路径跟随,这样跟随的效率不高。笔者设计了一种速度模糊控制器来控制机器人的速度V,使机器人以最有效的速度跟踪路径。差动单元的速度受到当前路径弯曲程度、前方路径弯曲程度以及差动单元的角速度三者的影响。本文中用虚曲率来表示当前路径及前方路径弯曲程度的一个合成结果,其表达式为[14]
| $ \rho = \left( {k_{\rm{r}}^{\rm{ \mathsf{ λ} }} - 1/2} \right)\rho {\rm{r}} + \left( {k_{\rm{f}}^{\rm{ \mathsf{ λ} }} - 1/2} \right)\rho {\rm{f,}} $ | (4) |
式中:ρ为虚曲率;ρr、ρf分别为当前路径点和前方路径点的曲率;kr,kf分别为权重系数的底数,取kr=3/2,kf=1/2;λ为权重系数的指数,其取值范围为[0, 1]。
所以,速度模糊控制器仍然是双输入单输出控制器,采用与图 5相同的模糊控制结构设计速度控制器,虚曲率ρ和角速度ω为输入,速度v为输出,通过调整合适的比例因子kρ、kω、kν分别将ρ、ω、v 3个变量映射到论域范围。
虚曲率ρ和角速度ω的模糊子集均取为{O(零),S(小),M(中),B(大)},速度不存在为零的情况,所以v的模糊子集为{VS(很小),S(小),M(中),B(大)}。速度控制器所有变量的模糊论域为[0, 6]。速度控制器也采取三角隶属函数,根据人工驾驶经验,总结出如表 2所示的控制规则表。
| 表 2 速度控制器规则表 |
针对本文中机器人的结构特点,小车的侧移、直角转弯及原地打转都可以直接通过先调整两驱动单元的角度,再采用不同的速度组合,很容易实现。所以,应用Matlab对具有代表性的正弦曲线进行路径跟随仿真实验,通过仿真过程的不断调试,最终整定得到的各控制参数如下。
角速度模糊控制器量化及比例因子:
| $ {K_y} = 1/40,{K_a} = 15,{K_\omega } = 0.3; $ |
速度模糊控制器量化及比例因子:
| $ {K_\rho } = = 3,{K_\omega } = 5.7,{K_\upsilon } = 83。$ |
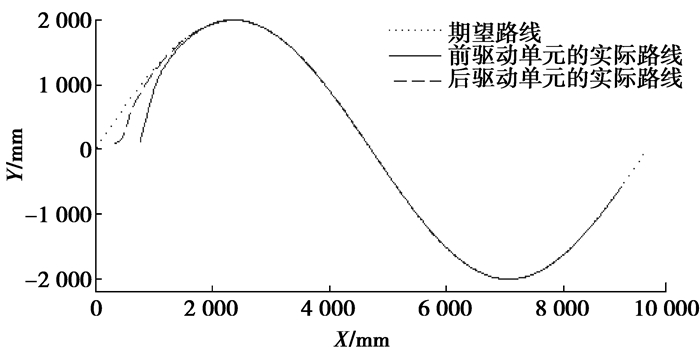
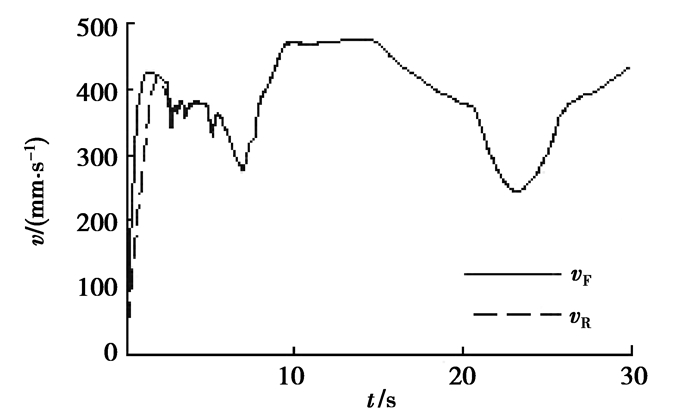
正弦曲线方程为:y=2 000·(x/1 500),全方位移动机器人初始位姿为:X=500,Y=100,θ=0,α1=π/3,α2=-π/6;图 6~10分别表示轨迹跟随、偏差减小及速度、加速度变化图,图中下标字母F表示前驱动单元,R表示后驱动单元。
|
图 6 跟踪正弦曲线轨迹图 |

|
图 7 横向偏差图 |

|
图 8 角度偏差图 |

|
图 9 角速度变化图 |
|
图 10 速度变化 |
由图 6、7、8可以看出,机器人能快速准确地跟随上期望路径且偏差超调量适中,在初始状态良好的情况下,没有超调,证明了该方法的有效性;由图 9、10可以看出,角速度控制稳定,不存在严重的振荡现象,且速度是连续变化的。此控制策略降低了控制的复杂程度,控制方法简单、准确。
4 结论1) 对具有两差动单元的四轮独立驱动移动机器人进行了运动学建模。
2) 提出了一种新型双点跟随方法,仿真证明了该方法的有效性,移动机器人能有效的跟随上期望路径。
3) 这里是以两驱动单元中心为参考点,没有AGV中心位姿解算单元,在后续的研究中应把单点控制和双点控制结合起来运用,达到更好的控制效果。
| [1] | 童艳. 移动机器人路径跟踪控制方法研究[D]. 西安: 西北工业大学硕士学位论文, 2007. |
| [2] | Chatzikomis C I, Spentzas K N. A path-following driver model with longitudinal and lateral control of vehicle's motion[J]. Forschung Ingenieurwesen, 2009, 73(4): 257–266. DOI:10.1007/s10010-009-0112-5 |
| [3] | Ono E, Hattori Y, Muragishi Y. Estimation of tire friction circle and vehicle dynamics integrated control for four-wheel distributed steering and four-wheel distributed traction/breaking systems[J]. R & D Review of Toyota CRDL, 2005, 40(4): 7–13. |
| [4] | Wang J M.Coordinated and reconfigurable vehicle dynamics control[D].Austin, USA:The University of Texas, 2007. |
| [5] | Wang J M, Longoria R G.Combined tire slip and slip angle tracking control for advanced vehicle dynamics control systems[C]//Proceedings of the 45th IEEE Conference on Decision and Control, December 13-15, 2006, San Diego, CA, USA. Piscataway:IEEE Press, 2006:1733-1738. |
| [6] |
阮久宏, 李贻斌, 杨福广, 等.
无人驾驶高速4WID-4WIS车辆路径跟踪单点预瞄控制[J]. 重庆大学学报, 2011, 34(10): 21–26.
RUAN Jiuhong, LI Yibin, YANG Fuguang, et al. Single-point preview control of unmanned high-speed 4WID-4WIS vehicle path tracking[J]. Journal of Chongqing University, 2011, 34(10): 21–26. (in Chinese) |
| [7] | Moriwaki K. Autonomous steering control for electric vehicles using nonlinear state feedback H∞control[J]. Nonlinear Analysis:Theory, Methods & Applications, 2005, 63(5/6/7): 2257–2268. |
| [8] | Fodrea L R.Obstacle avoidance control for the REMUS autonomous underwater vehicle[D].Monterey:Naval Postgraduate School, 2002. |
| [9] |
蔡成涛, 朱齐丹.
基于模糊控制器的移动机器人路径规划仿真[J]. 计算机仿真, 2008, 25(3): 182–185, 284.
CAI Chengtao, ZHU Qidan. Simulation of path planning for mobile robot based on fuzzy controller[J]. Computer Simulation, 2008, 25(3): 182–185, 284. (in Chinese) |
| [10] |
葛雪雁, 童艳, 徐宁.
移动机器人智能路径跟踪控制方法研究[J]. 工程建设与设计, 2007, 31(2): 52–55.
GE Xueyan, TONG Yan, XU Ning. Intelligent path following control for mobile robot[J]. Construction & Design for Project, 2007, 31(2): 52–55. (in Chinese) |
| [11] |
汤亚锋, 韦庆.
非完整移动机器人的反步跟踪控制方法[J]. 计算机仿真, 2007, 24(7): 168–175.
TANG Yafang, WEI Qing. Backstepping tracking control of nonholonomic mobile robot[J]. Computer Simulation, 2007, 24(7): 168–175. (in Chinese) |
| [12] |
李二超, 李炜.
一种机器人轨迹跟踪的单输入模糊控制[J]. 电气应用, 2007, 26(7): 91–93, 97.
LI Erchao, LI Wei. A single input fuzzy controller for robot tracking control[J]. Electrotechnical Application, 2007, 26(7): 91–93, 97. (in Chinese) |
| [13] | Zhenhai F A G, Liyong S B J.Optimal preview trajectory decision model of lane-keeping system with driver behavior simulation and artificial potential field[C]//Proceedings of the 2009 IEEE Intelligent Vehicles Symposium, June 3-5, 2009, Xi'an, China.Piscataway:IEEE Press, 2009:797-801. |
| [14] | Vinh T Q, Giap N H, Kim T W, et al.Adaptive robust fuzzy control and implementation for path tracking of mobile robot[C]//Proceedings of the 2009 IEEE International Symposium on Industrial Electronics, July 5-8, 2009, Seoul, Korea. 2009:1943-1949. |
 2013, Vol. 36
2013, Vol. 36


