2. 集美大学 机械工程学院, 福建 厦门 361021
2. College of Mechanical Engineering, Jimei University, Xiamen, Fujian 361021, China
随着中国经济的发展,多轴转向车辆的应用也越来越广泛。目前多轴转向车辆的转向方式有纯机械转向方式和机械与电控相结合的转向方式两种。采用机械和电控转向相结合的转向方式既能能保证车辆在电控转向失灵的情况下仍能安全行驶,有利于车辆行驶的可靠性,可提高车辆在高速行驶工况下的操纵稳定性[1],同时还可满足多模式转向要求。但如何解决机械转向和电控转向的耦合问题,是提高多轴转向车辆转向性能的重要因素。
国外对多轴转向车辆做了很多工作。如文献[2]分析了多轴车辆转向性能的影响因素,但未对车辆进行状态反馈控制。文献[3-5]虽然对多轴车辆的控制策略进行了不同研究,但控制方法相对比较复杂,实现较为困难。目前国内对多轴转向车辆的控制研究已取得一些成果,大多采用零侧偏角控制策略[6],也出现了如线性二次型最优控制[7]、H2/H∞控制[8]、横摆角速度反馈控制[9]、模糊PID控制[1]等,但大多把车辆的前轮看作是电控转向,部分文献把车辆的前轴车轮转角看作干扰信号,这和实际有所出入。
为了考虑前轴机械转向对车辆的影响,笔者对多轴转向车辆的动力学模型进行了改进,将模型转化为纯电控转向车辆的数学模型,避免了前轴机械转向给转向控制带来的困难。在改进的模型基础上,采用模型跟踪控制对某三轴车辆进行了转向控制研究,分析了车辆在不同车速下车辆的横摆角速度和质心侧偏角的跟踪效果,并且得到这两者在不同车速下的频域特性。
1 多轴转向车辆操纵模型图 1为线性两自由度多轴转向车辆模型图,图中车辆行驶方向为x轴正方向,垂直地面向上方向为z轴正方向,y轴方向根据右手定则确定[10]。
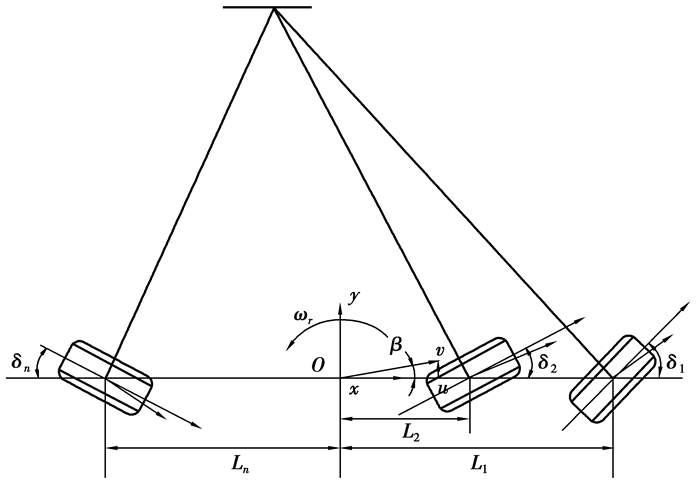
|
图 1 线性两自由度多轴转向车辆模型 |
| $ \mathit{\boldsymbol{P\dot x}} + \mathit{\boldsymbol{Qx}} = \mathit{\boldsymbol{R\delta }}, $ | (1) |
式中:
| $ \mathit{\boldsymbol{P = }}\left[ {\begin{array}{*{20}{c}} 0&{mu}\\ {{I_z}}&0 \end{array}} \right];\mathit{\boldsymbol{x}} = {\left[ {\begin{array}{*{20}{c}} {{\omega _{\rm{r}}}}&\beta \end{array}} \right]^{\rm{T}}}; $ |
| $ \mathit{\boldsymbol{Q}} = \left[ {\begin{array}{*{20}{c}} {mu + \frac{1}{u}\sum\limits_{i = 1}^n {{C_i}{L_i}} }&{\sum\limits_{i = 1}^n {{C_i}} }\\ {\frac{1}{u}\sum\limits_{i = 1}^n {{C_i}L_i^2} }&{\sum\limits_{i = 1}^n {{C_i}{L_i}} } \end{array}} \right]; $ |
| $ \mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} {{C_1}}& \cdots &{{C_n}}\\ {{C_1}{L_1}}& \cdots &{{C_n}{L_n}} \end{array}} \right]; $ |
| $ \mathit{\boldsymbol{\delta }} = {\left[ {\begin{array}{*{20}{c}} {{\delta _1}}& \cdots &{{\delta _n}} \end{array}} \right]^{\rm{T}}}。$ |
其中:m为车辆的总质量;δi为i轴车轮的转角;u、v分别为车辆质心速度在x、y轴的分量;Ci为i轴的综合侧偏刚度;ωr为车辆绕z轴的角速度;β为质心处的侧偏角,
一般情况下车辆的第1轴车轮转角信号是很重要的参考信号,不是控制输入也不能看作是干扰信号,为了避免对前轮转角处理不当,对动力学模型进行了处理,令
| $ {u_i} = {\delta _{i + 1}} + {a_i}{\delta _1}\;\;\;\left( {i = 1,2, \cdots ,n - 1} \right), $ | (2) |
则动力学模型变换为
| $ \mathit{\boldsymbol{P\dot x}} + \mathit{\boldsymbol{Qx}} = \mathit{\boldsymbol{R'u}}, $ | (3) |
式中:
| $ \mathit{\boldsymbol{R'}} = \left[ {\begin{array}{*{20}{c}} {{C_2}}& \cdots &{{C_n}}\\ {{C_2}{L_2}}& \cdots &{{C_n}{L_n}} \end{array}} \right];\mathit{\boldsymbol{u}} = \left[ {\begin{array}{*{20}{c}} {{\delta _2} + {a_1}{\delta _1}}\\ \vdots \\ {{\delta _n} + {a_{n - 1}}{\delta _1}} \end{array}} \right]。$ |
要使两动力学模型(式(1)和式(3))等同,必须满足以下条件:
| $ \left\{ \begin{array}{l} \sum\limits_{i = 1}^{n - 1} {{a_i}{C_{i + 1}}} = {C_1},\\ \sum\limits_{i = 1}^{n - 1} {{a_i}{C_{i + 1}}{L_{i + 1}}} = {C_1}{L_1}。\end{array} \right. $ | (4) |
通过式(4)求出ai,即可得到车辆的动力学方程。从式(4)可以看出,当车辆的轴数为3时,方程组有唯一解,当车辆的轴数大于3时,方程组有无穷多解,可以适当选择其中一个解即可求出车辆的动力学方程。
模型进一步可变换为
| $ \mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{Ax}} + \mathit{\boldsymbol{Bu}}, $ | (5) |
式中:A=-P-1Q;B=-P-1R′。
车辆的状态可表示为
| $ \mathit{\boldsymbol{y}} = {C_m}\mathit{\boldsymbol{x}}, $ | (6) |
式中Cm=I2×2。
从式(3)可以看出:转化后的模型中的控制量为u,对u进行简单的数学运算,就可以得到其他车轴车轮的转角,降低了对车辆控制的难度。
2 跟踪参考目标的确定如果设计的转向控制系统能够使车辆在转向时跟踪理想情况下的横摆角速度和质心侧偏角,则无疑能够大大提高汽车的安全性和操纵稳定性。为了保证车辆的稳定性,一般要求车辆质心处的侧偏角为0。结合文献设定车辆跟踪的稳态值为[15]
| $ {\omega _0} = \frac{u}{{{L_1}\left( {1 + K{u^2}} \right)}}{\delta _1} = {\omega _{\rm{t}}}{\delta _1}, $ | (7) |
| $ {\beta _0} = {\beta _{\rm{t}}}{\delta _1} = 0, $ | (8) |
式中:K为车辆的稳定性系数,K>0,K=0,K<0分别表示车辆不足转向、中性转向和过多转向。
由于一阶系统具有形式简单、超调量小等优点,所以把一阶系统作为理想的跟踪模型,则理想的参考模型为
| $ \left\{ \begin{array}{l} {\omega _{\rm{d}}} = \frac{{{\omega _0}}}{{1 + {\tau _\omega }s}},\\ {\beta _{\rm{d}}} = \frac{{{\beta _0}}}{{1 + {\tau _\beta }s}}。\end{array} \right. $ | (9) |
理想跟踪模型写成矩阵的形式为
| $ {{\mathit{\boldsymbol{\dot x}}}_{\rm{d}}} = {\mathit{\boldsymbol{A}}_{\rm{d}}}{\mathit{\boldsymbol{x}}_{\rm{d}}} + {\mathit{\boldsymbol{B}}_{\rm{d}}}{\delta _1}, $ | (10) |
| $ {\mathit{\boldsymbol{y}}_{\rm{d}}} = {\mathit{\boldsymbol{C}}_{\rm{d}}}{\mathit{\boldsymbol{x}}_{\rm{d}}}, $ | (11) |
式中:
| $ {{\mathit{\boldsymbol{\dot x}}}_{\rm{d}}} = {\left[ {\begin{array}{*{20}{c}} {{\omega _{\rm{d}}}}&{{\beta _{\rm{d}}}} \end{array}} \right]^{\rm{T}}};{\mathit{\boldsymbol{A}}_{\rm{d}}} = \left[ {\begin{array}{*{20}{c}} { - \frac{1}{{{\tau _\omega }}}}&0\\ 0&{ - \frac{1}{{{\tau _\beta }}}} \end{array}} \right]; $ |
| $ {\mathit{\boldsymbol{B}}_{\rm{d}}} = {\left[ {\begin{array}{*{20}{c}} {\frac{{{\omega _{\rm{t}}}}}{{{\tau _\omega }}}}&{\frac{{{\beta _{\rm{t}}}}}{{{\tau _\beta }}}} \end{array}} \right]^{\rm{T}}};{\mathit{\boldsymbol{C}}_{\rm{d}}} = \left[ {\begin{array}{*{20}{c}} 1&0\\ 0&1 \end{array}} \right]。$ |
其中τω、τβ为时间常数,其值越小,系统达到稳定的时间就越短,实际中可根据情况调整。
3 控制策略采用模型跟踪控制策略,使车辆的横摆角速度和侧偏角都能很好地跟踪理想模型。要使系统的输出逼近理想模型的输出,只要使实车的状态逼近理想车辆模型的状态,即系统的状态和理想车辆的状态之差趋近于0[16]。
跟踪误差向量e=x-xd,由实车模型和理想模型得到
| $ \mathit{\boldsymbol{\dot e}} = \mathit{\boldsymbol{Ax}} + \mathit{\boldsymbol{Bu}} - {\mathit{\boldsymbol{A}}_{\rm{d}}}{\mathit{\boldsymbol{x}}_{\rm{d}}} - {\mathit{\boldsymbol{B}}_{\rm{d}}}{\delta _1}。$ | (12) |
后几轴车轮转角由3部分构成,一部分正比于前轮转角,第2部分和车辆的实际运行状态有关,第3部分和车辆的跟踪模型状态有关,因此规定控制律的设计为
| $ \mathit{\boldsymbol{u}} = {\mathit{\boldsymbol{K}}_x}\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{K}}_{\rm{d}}}{\mathit{\boldsymbol{x}}_{\rm{d}}} + {\mathit{\boldsymbol{K}}_1}{\delta _1}。$ | (13) |
将式(13)代入式(12),并设若式(12)变化为如下形式
| $ \mathit{\boldsymbol{\dot e}} = \left( {\mathit{\boldsymbol{A}} + \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{K}}_x}} \right)\mathit{\boldsymbol{e}}, $ | (14) |
则控制律中Kd和K1的表达式分别为
| $ {\mathit{\boldsymbol{K}}_{\rm{d}}} = {\rm{pinv}}\left( \mathit{\boldsymbol{B}} \right)\left( {{\mathit{\boldsymbol{A}}_{\rm{d}}} - \mathit{\boldsymbol{A}}} \right) - {\mathit{\boldsymbol{K}}_{\rm{x}}}, $ | (15) |
| $ {\mathit{\boldsymbol{K}}_1} = {\rm{pinv}}\left( \mathit{\boldsymbol{B}} \right){\mathit{\boldsymbol{B}}_{\rm{d}}}, $ | (16) |
式中pinv(B)为矩阵B的伪逆矩阵。
跟踪控制结构框图如图 2。
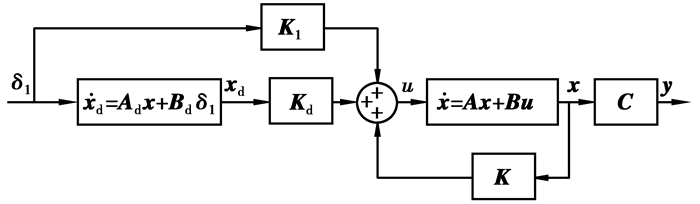
|
图 2 多轴电控转向车辆控制系统框图 |
从式(15)和图 2可以看出:系统的响应时间可由Kx进行调整,选择Kx时必须保证系统稳定,即矩阵A+BKx所有特征值均具有负实部。本文Kx是根据期望闭环特征值和极点配置算法获得,具体如下[17]:
1) 给定2个期望闭环特征值{λ1*, λ2*},若矩阵A非循环,选取一个(n-1)×2实常阵Kk,使A=(A-BKk)为循环;若矩阵A循环,取A=A。
2) 对循环A,选取一个(n-1)×1实常数向量ρ,取b=Bρ,使{A, b}为完全能控。
3) 计算矩阵A特征多项式和期望闭环特征值决定的特征多项式分别为
| $ \det \left( {s\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{A}}} \right) = \alpha \left( s \right) = {s^2} + {a_1}s + {a_0}, $ |
| $ {\alpha ^ * }\left( s \right) = \prod\limits_{i = 1}^2 {\left( {s - \lambda _i^ * } \right)} = {s^2} + a_1^ * s + a_0^ * 。$ |
4) Kx由公式(17)获得,
| $ \left. \begin{array}{l} 当矩阵\;\mathit{\boldsymbol{A}}\;循环时,{\mathit{\boldsymbol{K}}_x} = \mathit{\boldsymbol{\rho \bar K\bar Q}};\\ 当矩阵\;\mathit{\boldsymbol{A}}\;非循环时,{\mathit{\boldsymbol{K}}_x} = \mathit{\boldsymbol{\rho \bar K\bar Q}} + {\mathit{\boldsymbol{K}}_k}. \end{array} \right\} $ | (17) |
式中:K=[a0*-a0 a1*-a1];Q=P-1;
以某三轴转向车辆为例,此车第1轴机械转向,第2、3轴电控转向。此三轴转向车辆的主要技术参数见表 1。
| 表 1 主要计算技术参数 |
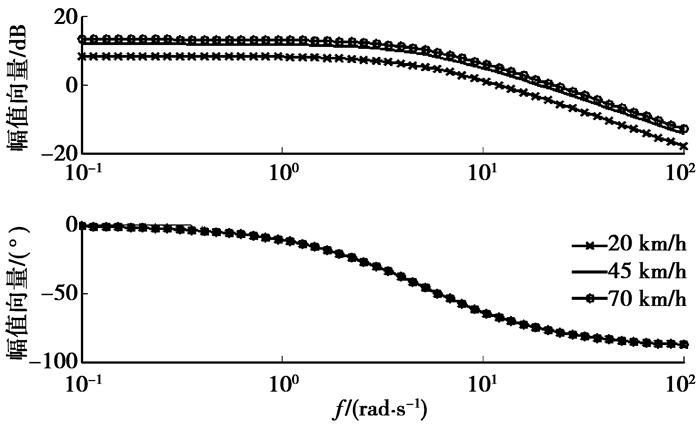
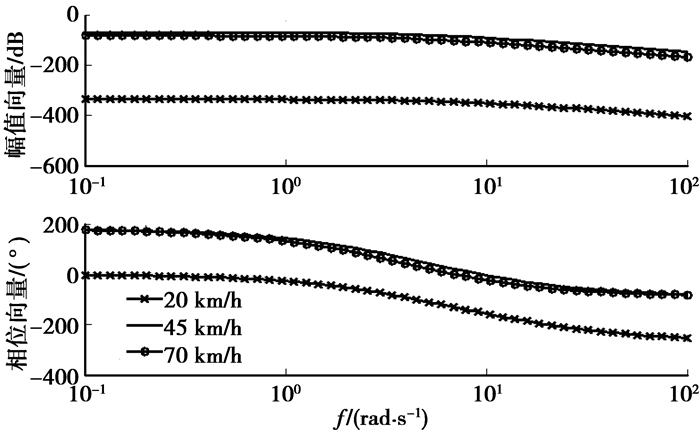
以车速为20、45和70 km/h进行仿真,前轮转角阶跃输入幅值为5°阶跃,车辆的稳定性系数K=0.002,τω=0.3,τβ=0.25,期望特征值为λ1*=-1+i,λ2*=-1-i,由于理想模型和实际车辆的初始条件不一定相同,分析时选择的理想模型和实际车辆的初始条件不同进行分析。图 3和4为前轮电控转向的多轴转向车辆的模型跟踪控制结果。同时分析了在不同车速下车辆的频域特性,如图 5和6所示。
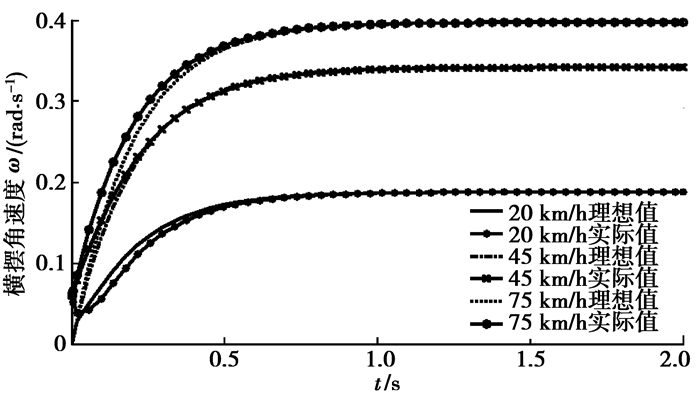
|
图 3 横摆角速度控制结果 |
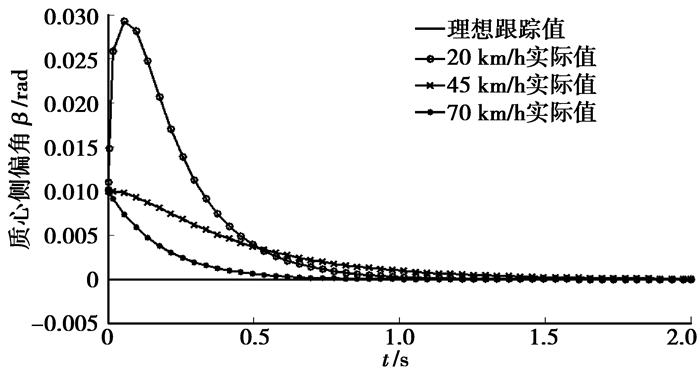
|
图 4 质心侧偏角控制结果 |
|
图 5 横摆角速度频域特性对比 |
|
图 6 质心侧偏角频域特性对比 |
从图 3和4可知:采用模型跟踪控制的车辆在不同的车速下都能很好地跟踪控制目标。车辆的横摆角速度在不同车速下不产生超调量。车辆质心侧偏角在低速时会产生一定的超调量,但高速时不会产生超调量,而且在高速时质心侧偏角达到稳定值的时间较低速时少,这有利于车辆高速时的稳定。
从图 5和6可以看出:横摆角速度的相位向量曲线几乎相同,但质心处的侧偏角在高速时相频特性优于低速,响应较为快速。从总体上看,采用模型跟踪控制的多轴转向车辆在高速时的系统频率响应较低速时更快捷,转向更平稳,对车辆高速时的稳定性有利。
5 结论1) 对多轴车辆的转向模型进行改进,将前轴机械转向的车轮转角隐含到控制变量中,降低了对多轴车辆转向控制的难度。
2) 在改进的动力学模型的基础上,结合极点配置算法对多轴车辆采用模型跟踪控制设计了相应的控制器。
3) 对某三轴车辆利用模型跟踪控制进行转向分析,得到该车辆能较好地跟踪理想模型所要求的控制目标,能保证车辆在高速行驶情况下,车辆的横摆角速度和质心侧偏角都不存在超调量,系统响应时间较快,控制平稳,提高了车辆的稳定性。
| [1] | 韩汪利. 多轴车辆转向控制系统设计及仿真[D]. 长沙: 湖南大学硕士学位论文, 2011. |
| [2] | Watanabe K, Yamakawa J, Tanaka M, et al. Turning characteristics of multi-axle vehicles[J]. Journal of Terramechanics, 2007, 44(1): 81–87. DOI:10.1016/j.jterra.2006.01.007 |
| [3] | Bayer K, Unlusoy Y S. Steering strategies for multi-axle vehicles[J]. International Journal of Heavy Vehicle Systems, 2008, 15(2/3/4): 208–236. DOI:10.1504/IJHVS.2008.022243 |
| [4] | An S J, Yi K, Jung G, et al. Desired yaw rate and steering control method during cornering for a six wheeled vehicle[J]. International Journal of Automotive Technology, 2008, 9(2): 173–181. DOI:10.1007/s12239-008-0022-9 |
| [5] | Moon K H, Lee S H, Chang S, et al. Method for control of steering angles for articulated vehicles using virtual rigid axles[J]. International Journal of Automotive Technology, 2009, 10(4): 441–449. DOI:10.1007/s12239-009-0050-0 |
| [6] | Wang S F, Zhang J Y, Li H S. Steering performance simulation of three-axle vehicle with multi-axle dynamic steering[C]//Proceedings of the 2008 IEEE Vehicle Power and Propulsion Conference(VPPC), September 3-5, 2008, Harbin, China. Piscataway:IEEE Press, 2008:1-5. |
| [7] | 李华师. 多轴转向车辆操纵稳定性控制策略研究[D]. 淄博: 山东理工大学硕士学位论文, 2010. |
| [8] |
王云超, 高秀华, 胡景煌, 等.
多轴转向车辆转向系统的H2/H∞混合控制[J]. 重庆工学院学报:自然科学版, 2008, 22(8): 6–10.
WANG Yunchao, GAO Xiuhua, HU Jinghuang, et al. Mixed H2/H∞ control for multi-axle steering vehicle[J]. Journal of Chongqing Institute of Technology:Natural Science, 2008, 22(8): 6–10. (in Chinese) |
| [9] | 杨波. 计及车架弹性的多轴重型越野车整车动态性能研究[D]. 武汉: 华中科技大学博士学位论文, 2004. |
| [10] | 王云超. 多轴转向车辆转向性能研究[D]. 长春: 吉林大学博士学位论文, 2007. |
| [11] | Chu L, Gao X Z, Guo J H, et al. Coordinated control of electronic stability program and active front steering[J]. Procedia Environmental Sciences, 2012, 12(B): 1379–1386. |
| [12] | Rangavajhula K, Tsao H S J. Active trailer steering control of an articulated system with a tractor and three full trailers for tractor-track following[J]. International Journal of Heavy Vehicle Systems, 2007, 14(3): 271–293. DOI:10.1504/IJHVS.2007.015604 |
| [13] | Wu D H, Hai J. Analysis of dynamic lateral response for a multi-axle-steering tractor and traile[J]. International Journal of Heavy Vehicle Systems, 2003, 10(4): 281–294. DOI:10.1504/IJHVS.2003.003694 |
| [14] | Zheng B, Anwar S. Yaw stability control of a steer-by-wire equresearch article[J]. Mechatronics, 2009, 19(6): 799–804. DOI:10.1016/j.mechatronics.2009.04.005 |
| [15] | Wang J, Wang Q, Jin L, et al. Independent wheel torque control of 4WD electric vehicle for differential drive assisted steering[J]. Mechatronics, 2011, 21(1): 63–76. DOI:10.1016/j.mechatronics.2010.08.005 |
| [16] |
曾长操, 刘奋, 张建武.
智能转向汽车的模型跟踪控制[J]. 上海交通大学学报, 2003, 37(11): 1763–1766.
ZENG Changcao, LIU Fen, ZHANG Jianwu. Model following control of automated steering vehicle[J]. Journal of Shanghai Jiaotong University, 2003, 37(11): 1763–1766. DOI:10.3321/j.issn:1006-2467.2003.11.030 (in Chinese) |
| [17] | 郑大钟. 线性系统理论[M]. 2版. 北京: 清华大学出版社, 2002. |
 2013, Vol. 36
2013, Vol. 36


