滚珠丝杠副是一种可将旋转运动和直线运动相互转换的机械装置，通过滚珠的自转与公转运动实现动力传递。滚珠与丝杠和螺母的接触特性是影响滚珠丝杠副传动精度、摩擦特性和可靠性的关键因素，近年来被广泛研究。

程光仁等^[1]最早采用Hertz理论对滚珠丝杠副的接触变形进行了研究, 但忽略了螺旋角的影响；Wei等^[2-3]建立了滚珠丝杠副动力学模型，并引用Hertz理论和滚动轴承中分析接触角变化的方法对滚珠丝杠副的接触变形进行了研究；许向荣等^[4]根据Hertz理论，推导了单螺母滚珠丝杠副的轴向刚度计算公式并分析了其影响因素；姜洪奎等^[5]考虑螺旋角的因素，建立了滚珠丝杠副的受力模型，应用微分几何理论推导了螺旋面的主曲率，并进一步分析了螺旋角对滚珠丝杠副弹性变形的影响；芮执元等^[6]考虑螺旋角和滚珠与滚道接触面的滑动、滚动摩擦，研究了滚珠丝杠副的轴向弹性变形，利用有限元方法进行了仿真分析；王福吉等^[7]采用Hertz接触理论推导了滚珠丝杠副轴向接触刚度的求解公式，从滚珠丝杠副轴向负载、设计参数和材料属性等方面分析了滚珠丝杠副的接触特性，运用有限元分析软件ANSYS对滚珠与丝杠滚道的接触问题进行仿真分析；牟世刚等^[8]建立了轴向载荷作用下的高速滚珠丝杠副动力学模型，采用数值分析方法计算了不同运行工况对滚珠丝杠副力学特性的影响。现有文献中关于滚珠丝杠副接触特性的研究多假设丝杠侧法向力与螺母侧法向力相等进行静态接触变形计算，而滚珠丝杠副在实际运转过程中，由于接触角随着轴向负载和丝杠转速的变化而变化，且离心力的作用会导致两侧法向力不相等使得接触变形量随之发生变化。因此，动态接触特性是滚珠丝杠副研究的重要内容之一，但现有研究尚不充分。

笔者基于Hertz接触理论，考虑运转过程接触角的变化和滚珠自身离心力的影响，建立滚珠丝杠副力平衡关系，分析丝杠副滚道两侧接触角随运行工况的变化规律，研究不同运行工况和结构参数对滚珠丝杠副接触特性的影响。

1 动态接触变形求解模型 1.1 基于Hertz理论的接触变形

满足Hertz接触的两物体点接触时接触变形δ的表达式为^[9]

$ \delta = {\delta ^ * }\sqrt[3]{{\frac{1}{8}{{\left( {1.5E} \right)}^2}{Q^2}\sum \rho }}, $

(1)

式中：Q为作用在接触面上的法向力；$\sum \rho $为主曲率和；E为当量弹性模量，且$E = \frac{{1 - \mu _1^2}}{{{E_1}}} + \frac{{1 - \mu _2^2}}{{{E_2}}}$，其中，E₁、E₂分别为两接触物体的弹性模量，μ₁、μ₂分别为两接触物体的泊松比。

$ \sum \rho = \sum\limits_{i = 1}^2 {\sum\limits_{j = 2}^2 {{\rho _{ij}}} } , $

(2)

$ F\left( \rho \right) = \frac{{\left| {\left( {{\rho _{11}} - {\rho _{12}}} \right) - \left( {{\rho _{21}} - {\rho _{22}}} \right)} \right|}}{{\sum \rho }}。$

(3)

丝杠滚道面与滚珠在接触点处的主曲率：

$ {\rho _{11}} = {\rho _{12}} = \frac{2}{d},{\rho _{21}} = - \frac{1}{R},{\rho _{22}} = \frac{{2\cos \alpha \cos \lambda }}{{{d_0} - d\cos \alpha }}。$

(4)

螺母滚道面与滚珠在接触点处的主曲率：

$ {\rho _{11}} = {\rho _{12}} = \frac{2}{d},{\rho _{21}} = - \frac{1}{R},{\rho _{22}} = - \frac{{2\cos \alpha \cos \lambda }}{{{d_0} + d\cos \alpha }}。$

(5)

式(4)~(5)中：ρ_ij代表各个曲率半径；d₀表示滚珠丝杠副公称直径；R表示滚道曲率半径；d表示滚珠直径；α和λ分别表示滚珠丝杠副的接触角和螺旋角。式(1)中的δ^*可依据F(ρ)查表^[10]得出。

设滚珠、丝杠和螺母的材料均为轴承钢，故E₁=E₂=210 GPa，μ₁=μ₂=0.3，将其代入式(1)化简得接触点法向变形δ为

$ \delta = 2.7944 \times {10^{ - 4}} \cdot {\delta ^ * } \cdot \sqrt[3]{{{Q^2}\sum \rho }}。$

(6)

法向力与轴向力的关系为

$ Q = \frac{{{F_{\rm{a}}}}}{{N\sin \alpha \cos \lambda }}, $

(7)

式中：F_a为作用在螺母上的轴向力；N为滚珠个数。

由式(6)变换可得法向载荷与变形的关系为

$ Q = k \cdot {\delta ^{\frac{3}{2}}} $

(8)

其中，k为滚珠、丝杠及螺母接触面间的刚性系数且$k = 2.140\;75 \times {10^5} \cdot {\left( {\sum \rho } \right)^{ - 0.5}} \cdot {\left( {{\delta ^*}} \right)^{ - 1.5}}$。

1.2 运转过程动态参数求解 1.2.1 接触角

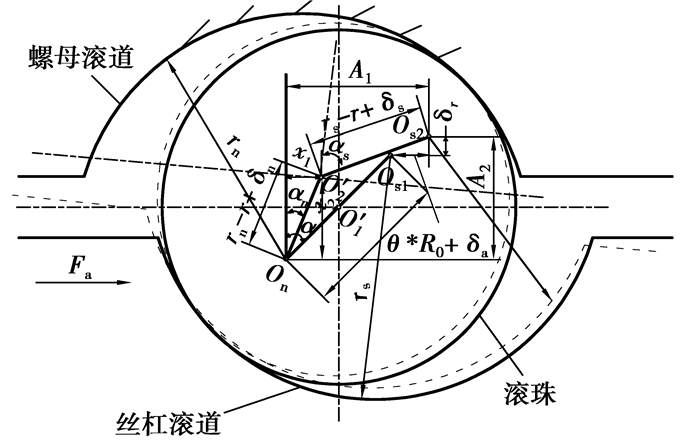
滚珠丝杠副中丝杠侧接触角和螺母侧接触角在设计时是相等的，但在实际运转过程中，滚动体与两滚道的接触角会发生变化，这是由于在轴向载荷作用下，接触变形引起滚珠中心和滚道曲率中心产生了位移。加载前后的滚珠中心、丝杠和螺母滚道曲率中心的位置关系如图 1所示^[11]。

图 1中，实线表示加载前，虚线表示加载后。O_n为螺母滚道曲率中心的位置，假设螺母中心在空间固定，${O_1}'$、${O_2}'$分别表示加载前后滚珠中心，O_s1、O_s2分别表示加载前后丝杠滚道曲率中心位置。r_s表示丝杠滚道曲率半径，r_n表示螺母滚道曲率半径，r表示滚珠半径，δ_s表示丝杠侧的接触变形，δ_n表示螺母侧的接触变形，δ_a表示丝杠轴向变形，δ_r表示丝杠径向变形，θ表示加载前后螺母与丝杠的相对角位移，R₀为加载前丝杠曲率中心距丝杠轴线的垂直距离，A₁和A₂分别表示丝杠曲率中心与螺母曲率中心水平方向和垂直方向的距离, x₁和x₂分别表示滚珠中心与螺母曲率中心水平方向和垂直方向的距离。文中下标s表示丝杠侧，下标n表示螺母侧。

由图 1可见，加载前3个中心O_n、O_s1、O_s2共线，故接触角相等，即为设计时的接触角α。加载后接触角发生变化，表现为丝杠侧接触角由α增大为α_s，螺母侧接触角由α减小为α_n。

依据图 1所示几何关系，由勾股定理可得：

$ \left. \begin{array}{l} {\left( {{A_1} - {x_1}} \right)^2} + {\left( {{A_2} - {x_2}} \right)^2} - {\left( {{r_{\rm{s}}} - r + {\delta _{\rm{s}}}} \right)^2} = 0,\\ x_1^2 + x_2^2 - {\left( {{r_{\rm{n}}} - r + {\delta _{\rm{n}}}} \right)^2} = 0。\end{array} \right\} $

(9)

$ \left. \begin{array}{l} \cos {\alpha _{\rm{n}}} = \frac{{{x_2}}}{{{r_{\rm{n}}} - r + {\delta _{\rm{n}}}}},\sin {\alpha _{\rm{n}}} = \frac{{{x_1}}}{{{r_{\rm{n}}} - r + {\delta _{\rm{n}}}}},\\ \cos {\alpha _{\rm{s}}} = \frac{{{A_2} - {x_2}}}{{{r_{\rm{s}}} - r + {\delta _{\rm{s}}}}},\sin {\alpha _{\rm{s}}} = \frac{{{A_1} - {x_1}}}{{{r_{\rm{n}}} - r + {\delta _{\rm{s}}}}}。\end{array} \right\} $

(10)

依据式(9)求得x₁和x₂并代入式(10)，即可求得加载后的接触角α_s和α_n。

1.2.2 滚珠公转角速度

滚珠运动中同时存在绕丝杠旋转轴的公转和绕自身轴线的自转^[12-13]，为便于计算离心力，先计算公转角速度

$ {\omega _{\rm{m}}} = \frac{{\omega \cdot A \cdot B}}{{A \cdot B + C \cdot D}}, $

(11)

其中：$r' = d/{d_0}$；$A = 1 - r' \cdot \cos {\alpha _{\rm{s}}}$，$B = \cos {\alpha _{\rm{n}}} + \tan \beta \cdot \cos {\alpha _{\rm{n}}}$，$C = 1 + r' \cdot \cos {\alpha _{\rm{n}}}$，$D = \cos {\alpha _{\rm{s}}} + \tan \beta \cdot \sin {\alpha _{\rm{s}}}$。

1.3 滚珠丝杠副力平衡关系

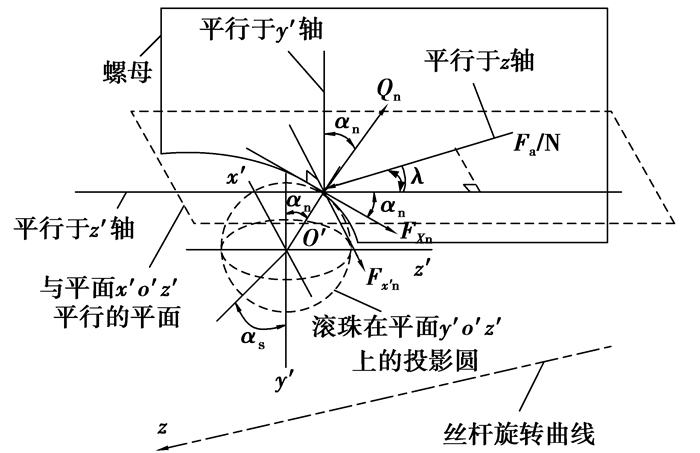
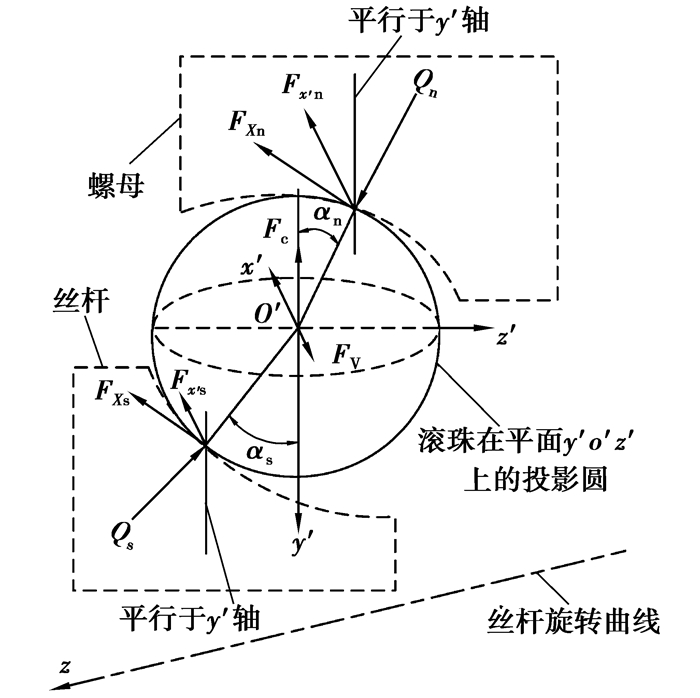
滚珠丝杠副中，滚珠和螺母承受的力主要有轴向载荷、接触点处法向力、接触点处摩擦力以及离心力等^[14]，根据各个力的特点进行滚珠丝杠副的受力分析得螺母和滚珠的力平衡关系图分别如图 2和图 3所示。其中各个坐标轴所代表的含义如下，z轴表示丝杠旋转轴线，坐标系o′-x′y′z′的坐标原点位于滚珠中心o′、x′为丝杠轨道上运动轨迹的切线方向，y′为垂直于丝杠面并指向z轴，z′位于丝杠表面并与x′、y′轴垂直。

根据图 2所示螺母的力平衡关系可得螺母的力平衡关系式为

$ {F_{\rm{a}}}/N - \left( {{Q_{\rm{n}}} \cdot \sin {\alpha _{\rm{n}}} + {F_{Xn}} \cdot \cos {\alpha _{\rm{n}}}} \right) \cdot \cos \lambda = 0。$

(12)

根据图 3所示滚珠的力平衡关系可得滚珠在y′方向上的力平衡关系式为

$ \begin{array}{*{20}{c}} { - {Q_{\rm{s}}} \cdot \cos {\alpha _{\rm{s}}} - {F_{{X_{\rm{s}}}}} \cdot \sin {\alpha _{\rm{s}}} + {Q_{\rm{n}}} \cdot \cos {\alpha _{\rm{n}}} - }\\ {{F_{X{\rm{n}}}} \cdot \sin {\alpha _{\rm{n}}} - {F_{\rm{c}}} = 0。} \end{array} $

(13)

式(12)和(13)中：F_c为作用于滚珠球心的离心力且${F_{\rm{c}}} = \frac{1}{2}m \cdot {d_0} \cdot \omega _{\rm{m}}^2$；F_Xn、F_x′n、F_Xs分别表示滚珠和滚道的摩擦力在相应方向上的分量；Q_s和Q_n分别表示螺母侧和丝杠侧的法向力。

式(12)和(13)中只有接触变形δ_s和δ_n是未知数，通过联立求解这两个方程即可求得δ_s和δ_n。

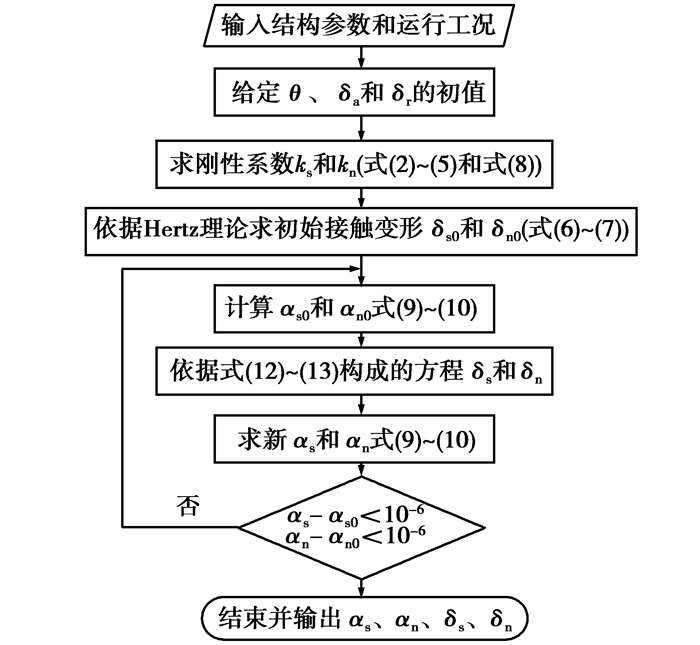
2 动态接触变形计算流程

依据上述所建模型，动态接触变形计算流程如图 4所示。以某一型号滚珠丝杠副结构参数进行计算，各参数值如表 1所示。

首先由式(6)和(7)求得初始接触变形δ_s0和δ_n0以及丝杠侧刚性系数k_s和螺母侧刚性系数k_n，然后将初始接触变形值代入式(9)求得x₁和x₂，进而将相关参数代入式(10)求出接触角α_s0和α_n0。最后将相关数据代入式(12)和式(13)，即得到新的考虑动态运转过程的接触变形值δ_s与δ_n，再将新的接触变形值代入式(9)求新的接触角α_s和α_n，如此循环直到α_s0-α_s和α_n0-α_n的差值都小于10^-6，这里10^-6为预设变化量，认为当差值为10^-6时变化量近似为零，此时输出最终的α_s、α_n、δ_s与δ_n。

3 结果与讨论 3.1 运行工况对接触变形的影响

在保证结构参数不变的前提下，改变轴向载荷F_a和丝杠转速n，求得相应工况下的接触角及接触变形如表 2所示。

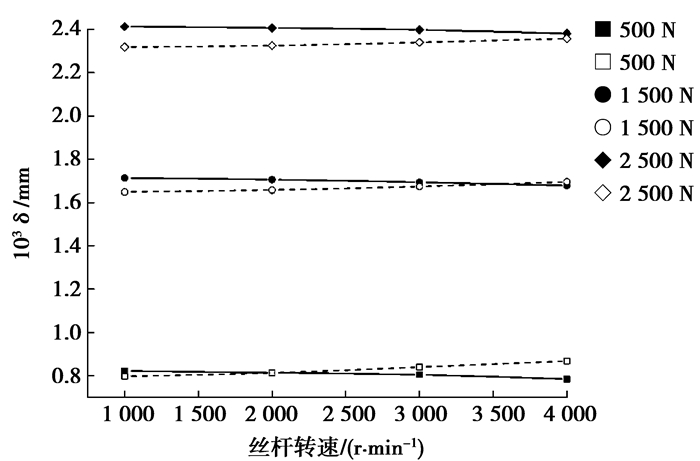
根据表 2所示数据，绘制不同轴向载荷下接触变形与丝杠转速的关系曲线如图 5所示。

由图 5可见，载荷越大，两侧接触变形的变化都越缓慢。无论在何种轴向载荷下，丝杠侧接触变形δ_s都随转速的增大而减小，螺母侧接触变形δ_n都随转速的增大而增大，δ_s的变化速度慢于δ_n，且δ_s与δ_n的差值随着转速的增大而减小。这是由于随着转速的增大，离心力增大，螺母侧法向力Q_n增大，丝杠侧法向力Q_s减小，最终导致Q_n > Q_s。可见，滚珠丝杠副的运行工况对接触变形有较大的影响，进一步影响滚珠丝杠副的定位精度。

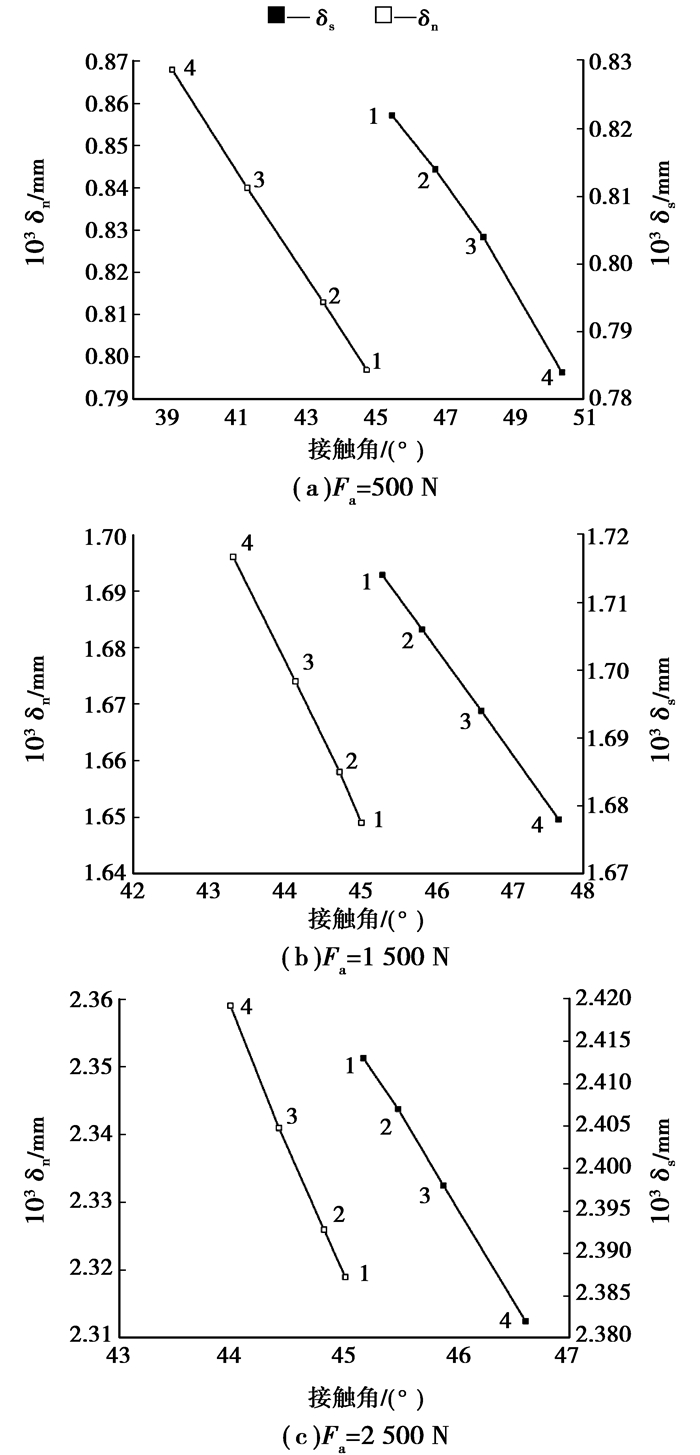
3.2 接触角对接触变形的影响

提取表 2所示数据，绘制螺母侧接触变形δ_n和丝杠侧接触变形δ_s随对应侧接触角变化的曲线如图 6所示，图 6(a)~(c)分别对应轴向载荷为500、1 500、2 500 N时的情况，每种轴向载荷均选取4种转速，其中1~4对应转速分别为1 000、2 000、3 000、4 000 r/min。

3.2.1 接触角的变化规律

结构的初始接触角为45°，综合图 6(a)~(c)可得，当载荷一定时，丝杠侧接触角α_s随转速的增大而增大，螺母侧接触角α_n随转速的增大而减小；两侧的接触角α_s和α_n的变化范围随着载荷增大而减小。两接触角的差值随转速增大而增大，因此当转速较高时不能将两侧接触角视为相等^[15]。当载荷小转速高时会引起较大的接触角变化，从而对滚珠丝杠副的动态性能产生显著影响，反之，当载荷大转速低时接触角变化很小，可认为两侧接触角相等。因此现有文献在分析时假定接触角不变并非在所有运行工况下都是合适的。

3.2.2 接触角变化对接触变形的影响

综合图 6(a)~(c)可得，两侧的接触变形都随着接触角的增大而减小，而且，随着转速增大，由于接触角α_s和α_n的变化趋势不一致，导致δ_s与δ_n的差值减小。接触角的变化速度越慢，接触变形的变化速度和也越慢。接触角的变化幅度越小，接触变形的变化幅度也越小。

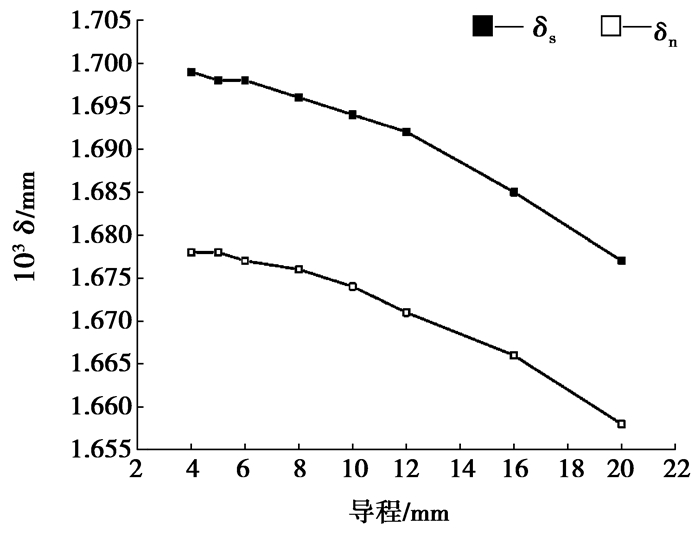
3.3 螺旋角对接触变形的影响

保持其他结构参数不变时，螺旋角只受导程的影响。当轴向载荷F_a=1 500 N，丝杠转速n=3 000 r/min时，取不同的导程求得相应的接触变形如表 3所示，同时可得丝杠侧接触变形δ_s和螺母侧接触变形δ_n随导程变化的曲线如图 7所示。

由图 7可见，在导程为4~6 mm，即螺旋角为2.28°~3.42°的范围内，两侧接触变形δ_s和δ_n变化不明显；在导程为6~20 mm，即螺旋角为3.42°~11.25°的范围内，接触变形变化幅度较大。随着导程的增大也即螺旋角的增大，δ_s和δ_n均减小。因而，实际应用中增大导程能减小接触变形进而提高滚珠丝杠副的性能。

4 结论

考虑运行工况引起的接触角变化和离心力，通过受力分析，建立了滚珠丝杠副的力平衡方程，从而建立了求解动态接触变形的模型。通过分析运行工况、接触角和螺旋角对接触变形的影响，所得结论如下：

1) 当载荷增大时，两侧接触变形的变化随转速的增大而变缓；转速增大时丝杠侧接触变形增大而螺母侧接触变形减小。

2) 接触变形随接触角的增大而减小，当载荷小转速高时接触角变化较大，而且两侧接触角的差值较大，因此分析中应该根据实际工况确定是否可近似认为两侧接触角相等。

3) 接触变形随螺旋角的增大而减小，且在螺旋角为3.42°~11.25°接触变化的变化速度加快，因此实际中可采用增大导程的办法提高滚珠丝杠副性能，但导程过大会增大轴向进给速度。因此，通过对滚珠丝杠副动态接触特性的分析可见，在提高滚珠丝杠定位精度时必须考虑运行工况并选取合适的结构参数。