2. 山东省电力公司滨州供电局, 山东 滨州 256600
2. Binzhou Power Supply Bureau, Shandong Power Company, Binzhou, Shandong 256600, China
在目前大功率LED照明的驱动电源中,普遍采用LC滤波电路来减小电路的输出纹波。电解电容具有能量密度大、价格低等优点,是滤波电容的首选[1-4]。由于LC滤波器的自身特点,导致输出有纹波残留。增大电容值可减小电路输出纹波,但会使得电路输出为电压源,与LED为电流型负载相矛盾[5-6]。更严重的是在LED照明应用环境下,电解电容的寿命不超过5 000 h,导致LED驱动电源的寿命与LED的长寿命(50 000 h以上)难以匹配[7-12]。
针对这种现象,笔者提出一种有源纹波补偿Buck型LED驱动电源拓扑结构[13-14]。该方案采用有源纹波补偿电路取代传统的电解电容滤波,将开关电源与线性电源有机融合。该融合型电源中无大容量电解电容,小型电容可以采用可靠性高的聚酯电容等容性元件,因此避免了驱动电源因大电解电容导致使用寿命不匹配问题。而补偿电路可与控制电路、开关管集成一体,使得LED驱动电源更易实现小型化和集成化。
笔者介绍了有源纹波补偿Buck电路的拓扑结构及工作原理。在此基础上,进一步研究了其主电路的小信号模型,得到了它的相关传递函数,以指导电路的设计:首先通过引入三端开关器件模型得到了有源补偿Buck电路的小信号模型。对该模型进行分析,分别得到了电感电流和补偿电流关于输入电压及占空比的传递函数,从而得到了输出电流的表达式。由输出电流表达式推出了输出电流关于输入电压及占空比的传递函数。用Matlab分析上述传递函数一阶因子的幅频和相频特性表明,在设计电路时只要参数选择得当,就可以将输入信号扰动完全滤除,使得输出电流扰动为零,得到的输出电流为直流。最后对该有源纹波补偿Buck型LED驱动电源进行了仿真分析和实验验证,证实了上述新型电路及其小信号模型的正确性。
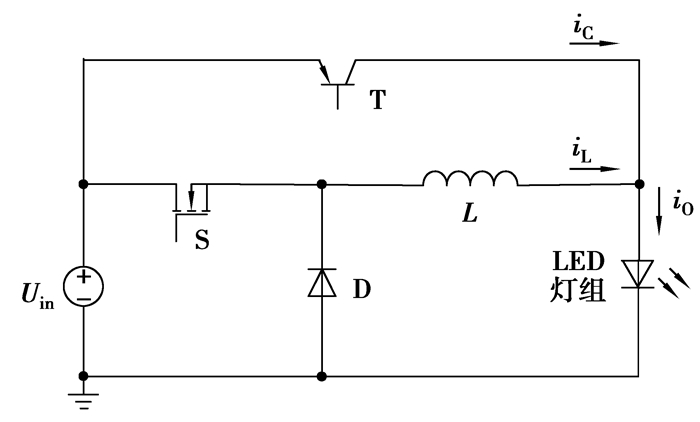
1 有源纹波补偿Buck电路拓扑结构及工作原理 1.1 电路拓扑结构电路如图 1所示:在传统的Buck电路基础上,去掉滤波电容,用辅助线性有源补偿电路对电感纹波电流进行补偿。图中由开关管S、电感L、LED灯组、续流二极管D组成Buck电路,工作于连续导通模式;三极管T为辅助补偿电路,工作于线性放大状态。
|
图 1 有源纹波补偿Buck电路拓扑 |
主电路电感电流iL和三极管T的集电极电流iC分别为
| $ {i_{\rm{L}}} = {I_{\rm{L}}} + {i_{\rm{r}}}, $ |
| $ {i_{\rm{C}}} = {I_{\rm{C}}} + {i_{\rm{C}}}, $ |
式中:IL和IC分别为电感电流和三极管T的集电极电流的直流分量;ir和iC分别为它们的交流分量。
当iC=-ir时,电路输出电流为
| $ {i_{\rm{O}}} = {i_{\rm{L}}} + {i_{\rm{C}}} = {I_{\rm{L}}} + {I_{\rm{C}}} = {I_{\rm{O}}}。$ | (1) |
通过LED的电流iO为恒定直流,实现了对电感纹波电流的全补偿。
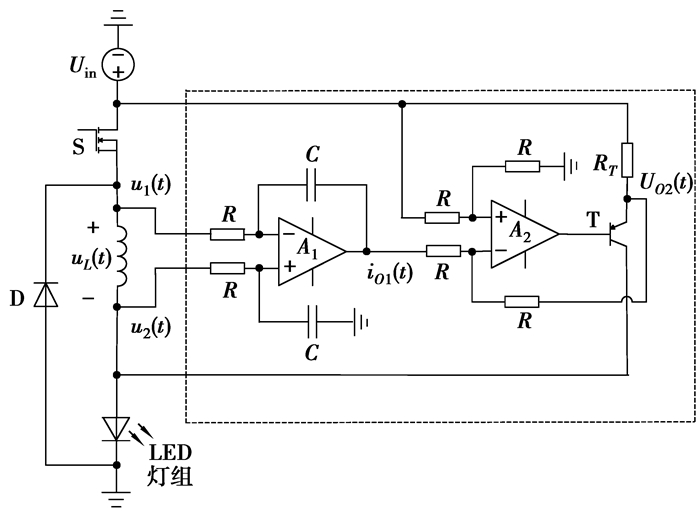
1.2 电感纹波电流检测与补偿这里采取观测电感两端的电压来检测纹波电流并予以补偿[15],如图 2所示。图中检测电路由运算放大器A1、电阻R、电容C组成差分积分器;运放A2组成减法器用以消除因供电电压Uin波动而导致的补偿电流变化。假设各元件均为理想器件,电感上电压和电流的关系为
|
图 2 纹波电流检测补偿电路图 |
| $ {u_{\rm{L}}}\left( t \right) = L\frac{{{\rm{d}}{i_{\rm{L}}}\left( t \right)}}{{{\rm{d}}t}} = L\frac{{{\rm{d}}\left( {{I_{\rm{L}}} + {i_{\rm{r}}}\left( t \right)} \right)}}{{{\rm{d}}t}} = L\frac{{{\rm{d}}{i_{\rm{r}}}\left( t \right)}}{{{\rm{d}}t}}。$ | (2) |
差分积分电路的输出电压为
| $ \begin{array}{l} {u_{O1}}\left( t \right) = \frac{1}{{RC}}\int {\left( {{u_2}\left( t \right) - {u_1}\left( t \right)} \right){\rm{d}}t} = - \frac{1}{{RC}}\int {{u_{\rm{L}}}\left( t \right){\rm{d}}t} \\ \;\;\;\;\;\;\;\;\; = - \frac{L}{{RC}}{i_{\rm{r}}}\left( t \right) + {U_{O1}}。\end{array} $ | (3) |
由后级减法电路可知:
| $ {u_{O2}}\left( t \right) = {U_{{\rm{in}}}} - {u_{O1}}\left( t \right)。$ | (4) |
进而得到三极管T中的补偿电流为
| $ {i_{\rm{C}}}\left( t \right) = \frac{{{U_{{\rm{in}}}} - {u_{O2}}\left( t \right)}}{{{R_{\rm{T}}}}} = \frac{{{u_{O1}}\left( t \right)}}{{{R_{\rm{T}}}}}。$ | (5) |
将式(3)代入式(5)得到补偿电流的表达式为
| $ \begin{array}{l} {i_{\rm{C}}}\left( t \right) = \frac{{{U_{O1}}}}{{{R_{\rm{T}}}}} - \frac{L}{{{R_{\rm{T}}}RC}}{i_{\rm{r}}}\left( t \right)\\ = \frac{L}{{{R_{\rm{T}}}RC}}\left( {\frac{{RC}}{L}{U_{O1}} - {i_{\rm{r}}}\left( t \right)} \right)。\end{array} $ | (6) |
由式(6)可知,补偿电流iC(t)包含一个交流分量和一个直流分量。当选择合适的电路元件参数使得L/RTRC=1时,补偿电流可表示为
| $ \begin{array}{*{20}{c}} {{i_{\rm{C}}}\left( t \right) = \frac{{RC}}{L}{U_{O1}} - {i_{\rm{r}}}\left( t \right)}\\ { = {I_{\rm{C}}} - {i_{\rm{r}}}\left( t \right)。} \end{array} $ | (7) |
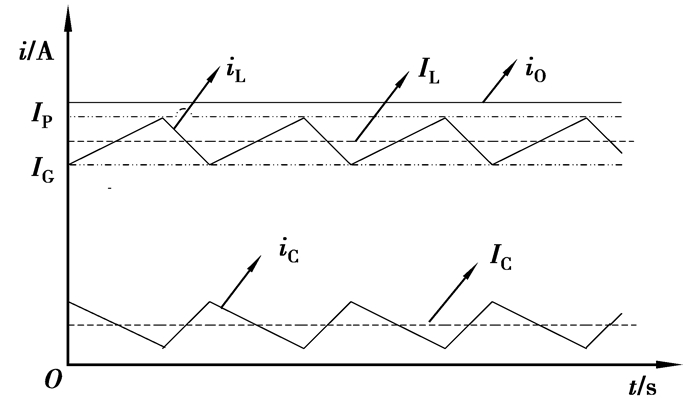
由式(7)可以看出,此时补偿电流的交流分量与电感纹波电流呈负比例关系,即iC(t)=-ir(t),实现了电感纹波电流的全补偿,补偿波形如图 3所示。
|
图 3 电感电流补偿示意图 |
由波形图可得电感直流分量IL的表达式为
| $ {I_{\rm{L}}} = \frac{1}{2}\left( {{I_{\rm{P}}} + {I_{\rm{G}}}} \right), $ | (8) |
其中IP和IG分别为电感电流的峰值和谷值。由式(7)可知补偿电流直流分量为
| $ {I_{\rm{C}}} = \frac{{RC}}{L}{U_{O1}}。$ | (9) |
补偿电路三极管T上的能量损耗为
| $ {P_{{\rm{LOSS}}}} = - {i_{\rm{C}}}{U_{{\rm{CE}}}} = \left( {1 - D} \right){U_{{\rm{in}}}}{I_{\rm{C}}}。$ | (10) |
为了减少补偿电路的能耗,提高电源效率,应该使IC的值尽量小。IC的临界最小值为
| $ {I_{\rm{C}}} = \frac{1}{2}\left( {{I_{\rm{P}}} - {I_{\rm{G}}}} \right)。$ | (11) |
结合式(8)、(9)和(11),得到运放A1输出的直流分量UO1和LED上的直流IO分别为
| $ {U_{O1}} = \frac{L}{{2RC}}\left( {{I_{\rm{P}}} - {I_{\rm{G}}}} \right), $ | (12) |
| $ {I_{\rm{O}}} = {I_{\rm{L}}} + {I_{\rm{C}}} = {I_{\rm{P}}}。$ | (13) |
从以上推导可以看出,纹波补偿电路将电感纹波电流完全补偿,使得通过LED的电流为恒定直流,其值为IP。
为求取IP的表达式,对传统Buck电路进行分析,其电感上的平均电流和纹波分别为
| $ {I_{{\rm{L}}\_{\rm{avg}}}} = \frac{{D{U_{{\rm{in}}}}}}{{{R_{{\rm{eq}}}}}}, $ | (14) |
| $ \Delta {i_{\rm{L}}} = \frac{{{U_{{\rm{in}}}}\left( {1 - D} \right)D{T_{\rm{S}}}}}{{2L}}。$ | (15) |
式中:D为开关占空比;TS为开关周期;Req为LED的直流等效电阻。由此可以得到IP的表达式为
| $ \begin{array}{l} {I_{\rm{P}}} = {I_{{\rm{L}}\_{\rm{avg}}}} + \Delta {i_{\rm{L}}}\\ \;\;\;\; = \frac{{{U_{{\rm{in}}}}D\left( {2L + \left( {1 - D} \right){T_{\rm{S}}}{R_{{\rm{eq}}}}} \right)}}{{2L{R_{{\rm{eq}}}}}}。\end{array} $ | (16) |
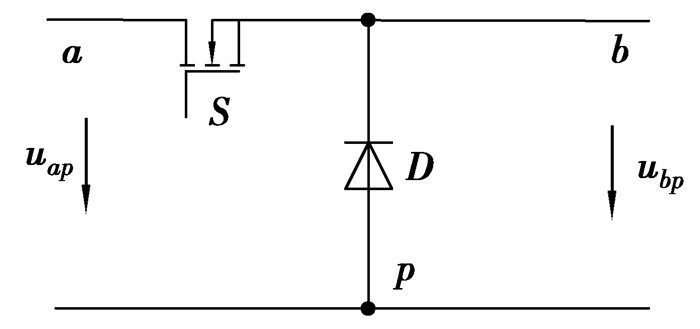
基于三端开关器件模型建立电路的小信号模型[16-18]。所谓三端开关器件模型就是把变换器的开关管和二极管作为整体看成一个三端开关器件,用其端口的平均电压、平均电流的关系来表征,然后把它适当地嵌入到具体的变换器中,构成平均值等效电路。如图 4所示:a端为有源端,p端为无源端,b端为公共端。
|
图 4 三端开关器件示意图 |
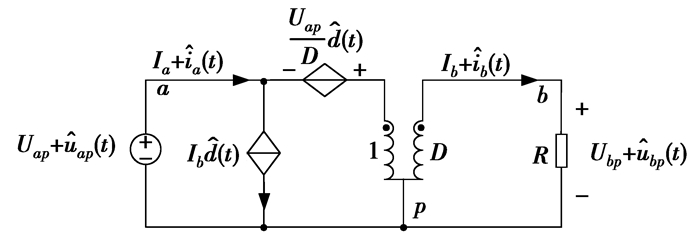
根据平均开关网络法等理论对开关变换器进行建模可得到PWM开关的等效电路模型,如图 5所示(R为等效负载)。令电路中参数的扰动量为零,可得到其直流工作模型;若令电路直流分量为零,则可得到其小信工作号模型。
|
图 5 三端开关器件等效模型 |
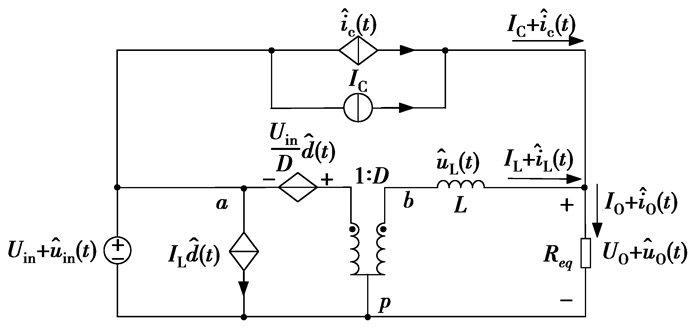
将三端开关器件的等效模型代入到有源纹波补偿Buck电路中,得到相应的等效电路模型。如图 6所示,其中Req为负载LED的等效电阻。
|
图 6 有源纹波补偿Buck等效电路模型 |
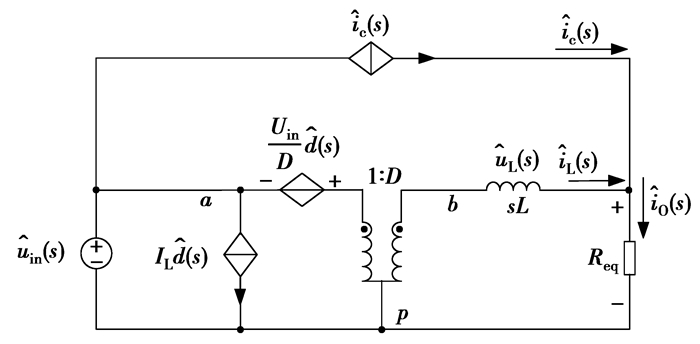
为了求得电路的传递函数,以分析电路的动态特性,令有源纹波补偿Buck电路等效模型中的直流分量为零,并将其转化到复频域,得到其交流小信号模型,如图 7所示。
|
图 7 电路小信号模型 |
图中
| $ {{\hat i}_{\rm{c}}}\left( s \right) = - \frac{1}{{s{R_{\rm{T}}}RC}}{{\hat u}_{\rm{L}}}\left( s \right)。$ | (17) |
由图 7所示小信号模型可知:
| $ {{\hat i}_{\rm{L}}}\left( s \right) = \frac{{{{\hat u}_{\rm{L}}}\left( s \right)}}{{sL}}, $ | (18) |
| $ {{\hat i}_{\rm{O}}}\left( s \right) = {{\hat i}_{\rm{c}}}\left( s \right) + {{\hat i}_{\rm{L}}}\left( s \right), $ | (19) |
| $ D{{\hat u}_{{\rm{in}}}}\left( s \right) + {U_{{\rm{in}}}}\hat d\left( s \right) = {{\hat u}_{\rm{L}}}\left( s \right) + {{\hat i}_{\rm{O}}}\left( s \right){R_{{\rm{eq}}}}。$ | (20) |
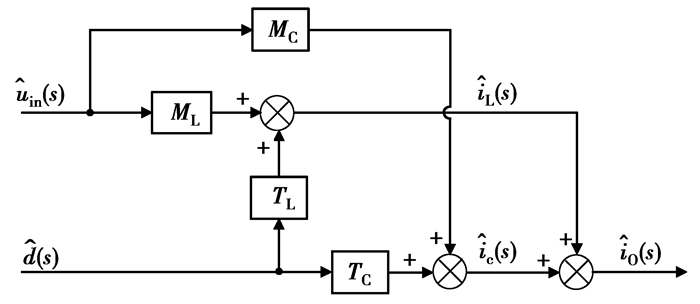
由上述方程式可知,电路中引入扰动量的参数是输入电压和占空比;输出电流由电感电流和补偿电流共同决定。因此,分别考虑各个扰动信号独立作用时的工作状况,得到电感电流、补偿电流关于输入电压及占空比的4个传递函数。进而得到电路的传递函数框图,如图 8所示。
|
图 8 有源纹波补偿Buck电路传递函数框图 |
图 8中各传递函数的意义如下:
ML:只有输入电压发生扰动时,电感电流对输入电压的传递函数:
| $ {M_{\rm{L}}} \equiv \frac{{{{\hat i}_{\rm{L}}}\left( s \right)}}{{{{\hat u}_{{\rm{in}}}}\left( s \right)}}\left| {_{\hat d\left( s \right) = 0}} \right. = \frac{{D{R_{\rm{T}}}RC}}{{\left( {{R_{\rm{T}}}RC - L} \right){R_{{\rm{eq}}}} + sL{R_{\rm{T}}}RC}}。$ | (21) |
MC:只有输入电压发生扰动时,补偿电流对输入电压的传递函数:
| $ {M_{\rm{C}}} \equiv \frac{{{{\hat i}_{\rm{c}}}\left( s \right)}}{{{{\hat u}_{{\rm{in}}}}\left( s \right)}}\left| {_{\hat d\left( s \right) = 0}} \right. = - \frac{{DL}}{{\left( {{R_{\rm{T}}}RC - L} \right){R_{{\rm{eq}}}} + sL{R_{\rm{T}}}RC}}。$ | (22) |
TL:仅在占空比发生变化时,电感电流对占空比的传递函数:
| $ {T_{\rm{L}}} \equiv \frac{{{{\hat i}_{\rm{L}}}\left( s \right)}}{{\hat d\left( s \right)}}\left| {_{{{\hat u}_{{\rm{in}}}}\left( s \right) = 0}} \right. = \frac{{{U_{{\rm{in}}}}{R_{\rm{T}}}RC}}{{\left( {{R_{\rm{T}}}RC - L} \right){R_{{\rm{eq}}}} + sL{R_{\rm{T}}}RC}}。$ | (23) |
TC:仅在占空比发生变化时,补偿电流对占空比的传递函数:
| $ {T_{\rm{C}}} \equiv \frac{{{{\hat i}_{\rm{c}}}\left( s \right)}}{{\hat d\left( s \right)}}\left| {_{{{\hat u}_{{\rm{in}}}}\left( s \right) = 0}} \right. = - \frac{{{U_{{\rm{in}}}}L}}{{\left( {{R_{\rm{T}}}RC - L} \right){R_{{\rm{eq}}}} + sL{R_{\rm{T}}}RC}}。$ | (24) |
由传递函数框图可得输出电流的表达式为
| $ \begin{array}{l} {{\hat i}_{\rm{O}}}\left( s \right) = \frac{{{R_{\rm{T}}}RC - L}}{{\left( {{R_{\rm{T}}}RC - L} \right){R_{{\rm{eq}}}} + sL{R_{\rm{T}}}RC}}\left( {D{{\hat u}_{{\rm{in}}}}\left( s \right) + } \right.\\ \left. {{U_{{\rm{in}}}}\hat d\left( s \right)} \right)。\end{array} $ | (25) |
根据式(25),分别求取输出电流对输入电压和占空比的传递函数,可以得到:
| $ \begin{array}{l} M\left( s \right) = \frac{{{{\hat i}_{\rm{O}}}\left( s \right)}}{{{{\hat u}_{{\rm{in}}}}\left( s \right)}}\left| {_{\hat d\left( s \right) = 0}} \right. = \frac{{D\left( {{R_{\rm{T}}}RC - L} \right)}}{{\left( {{R_{\rm{T}}}RC - L} \right){R_{{\rm{eq}}}} + sL{R_{\rm{T}}}RC}}\\ \;\;\;\;\;\;\;\;\; = {k_{\rm{D}}}\frac{1}{{1 + sT}}, \end{array} $ | (26) |
| $ \begin{array}{l} T\left( s \right) = \frac{{{{\hat i}_{\rm{O}}}\left( s \right)}}{{\hat d\left( s \right)}}\left| {_{{{\hat u}_{{\rm{in}}}}\left( s \right) = 0}} \right. = \frac{{{U_{{\rm{in}}}}\left( {{R_{\rm{T}}}RC - L} \right)}}{{\left( {{R_{\rm{T}}}RC - L} \right){R_{{\rm{eq}}}} + sL{R_{\rm{T}}}RC}}\\ \;\;\;\;\;\;\;\;\; = {k_{{\rm{in}}}}\frac{1}{{1 + sT}}, \end{array} $ | (27) |
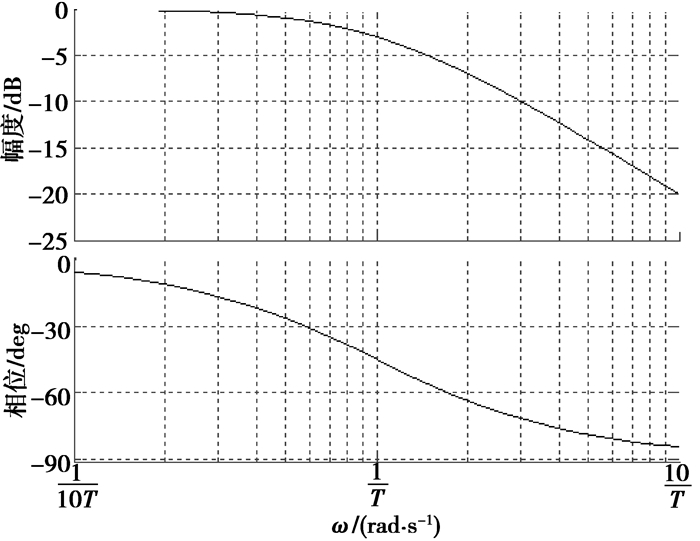
其中比例系数kD、kin、时间常数T的表达式分别为kD=D/Req、kin=Uin/Req、T=LRTRC/(RTRC-L)Req。由此可以看出传递函数M(s)和T(s)均为比例因子和一阶因子的乘积。一阶因子(1+sT)-1具有低通滤波特性,可以将输入信号中的高频成分衰减、滤除。用Matlab分析一阶因子(1+sT)-1幅频和相频特性,如图 9所示。
|
图 9 (1+sT)-1的波特图 |
由图 9可知设计电路时应使得时间常数T足够大,从而使得转折频率足够小,以增强传递函数的滤波效果。当选择电路元件参数使得RTRC=L时,T趋向于无穷大,转折频率为0。电路可将交流分量完全滤除,输出电流扰动
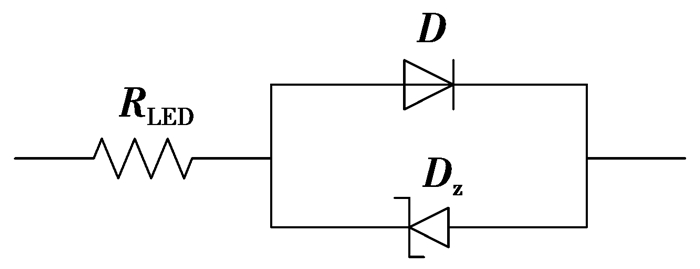
采用PSIM软件对图 2所示的纹波补偿Buck电路进行仿真实验。主电路的参数设置为:Uin=12 V,L=100 uH,开关频率fs=100 kHz,占空比D=85%;补偿电路的参数设置为:R=10 kΩ,C=0.01 uF,RT=1 Ω;LED是非线性元件,为便于分析,在这里引入LED的等效电路模型[8],如图 10所示。根据照明LED的实际参数,仿真中设定D和DZ的电压为:UD=3.0 V,RLED=0.6 Ω。
|
图 10 LED等效电路模型 |
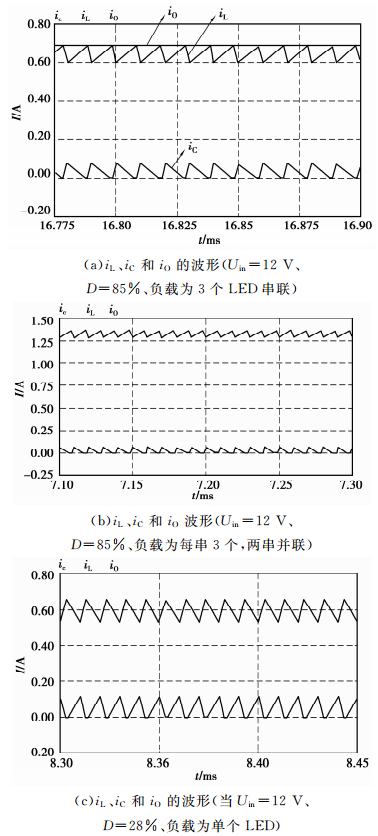
当负载为3个LED串联的灯组时,仿真得到电感电流、补偿电流和输出电流的波形如图 11(a)所示。由图可以看出ic(t)=-ir(t),补偿电流将电感纹波电流完全补偿,输出为0.67 A的直流。
|
图 11 仿真结果波形图 |
为了进一步验证该补偿电路的适应性,即在不同工况下的补偿效果,改变相关参数,进行后继仿真实验。将负载变为每串3个,两串并联的LED灯组,仿真得到如图 11(b)所示的波形图,其中IO=1.33 A;将负载变为单个LED,占空比相应地变为原来的1/3,即D=28.3%,得到如图 11(c)所示波形图,此时IO=0.66 A。由此可见,在不同的工况下,随着相关参数的改变,主电路电感电流也相应改变,但补偿电路能够很好地跟随补偿电感电流,输出电流为恒定直流。因此,该补偿电路有较好的适应性。
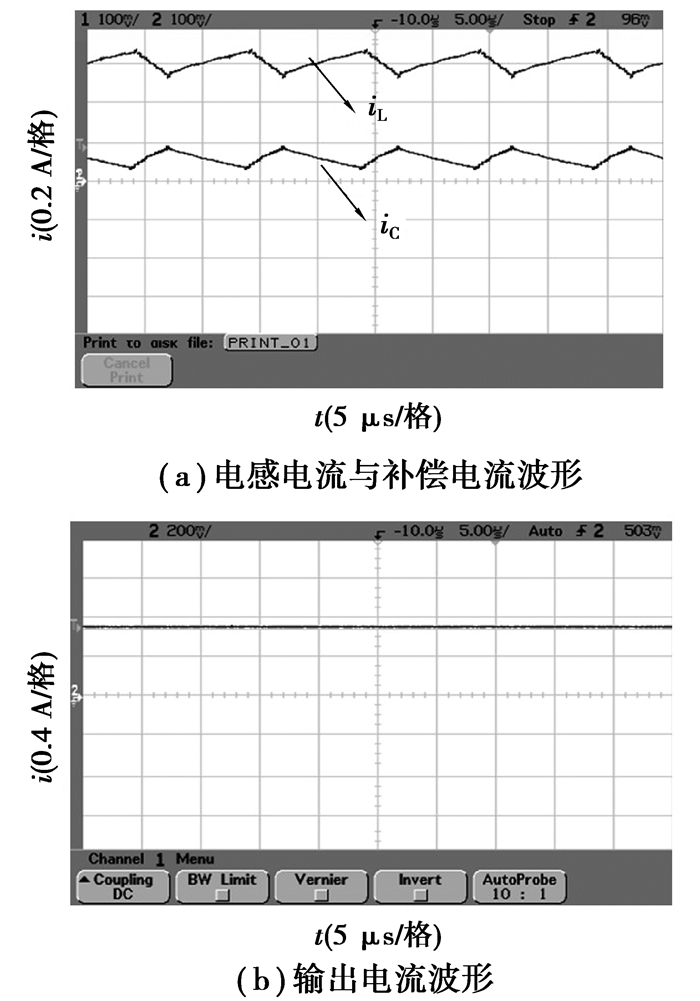
4.2 实验验证最后制作了该有源纹波补偿Buck电路的样机。主电路、纹波检测和补偿电路元件参数与仿真电路相同;负载LED灯组采用3个额定功率PW=3 W的大功率LED串联连接,每一个LED的导通电压范围为3.0~3.5 V,导通电流范围为0.6~1 A;控制电路采用UC3843峰值电流控制芯片,并附加射极跟随器实现斜坡补偿。实验结果如图 12所示。图 12(a)是电感电流iL 和补偿电流iC的波形, 图 12(b)为电路输出电流iO波形。实测输出电流为iO=0.73 A。在补偿电路上的损耗PLOSS=0.2 W,在补偿电路上的损耗较小,可以忽略。
|
图 12 实验波形图 |
有源纹波补偿Buck型LED驱动电源去掉了体积较大、使用寿命较短的电解电容,提高了电源的可靠性和使用寿命,也使之更易小型化和集成化。笔者介绍了该有源纹波补偿Buck电路的拓扑结构及工作原理,并在此基础上利用开关管的等效三端模型建立了有源纹波补偿Buck型拓扑的小信号模型。由小信号模型得到了输出电流表达式,进而推导出了输出电流关于输入电压及占空比的传递函数。用Matlab对传递函数的一阶因子进行幅频和相频特性分析,得到了实现电流纹波全补偿、获得直流输出的条件,即选择适当的元器件参数使RTRC=L。最后对该有源纹波补偿Buck电路进行了仿真和实验验证。实验结果与理论分析及仿真结果基本一致,进一步证实了该新型电路的可行性及其小信号模型的正确性。
| [1] |
廖志凌, 阮新波.
半导体照明工程的现状与发展趋势[J]. 电工技术学报, 2006, 21(9): 106–111.
LIAO Zhiling, RUAN Xinbo. Present status and developing trend of the semiconductor lighting[J]. Transactions of China Electrotechnical Society, 2006, 21(9): 106–111. (in Chinese) |
| [2] | Heffernan B, Frater L, Watson N. LED replacement for fluorescent tube lighting[C]//Proceedings of the 2007 Power Engineering Conference, AUPEC 2007, December 9-12, 2007, Perth, WA. Piscataway:IEEE Press, 2007:1-6. |
| [3] |
闫晓金, 潘艳, 陈永真.
开关电源对电解电容器性能的基本要求[J]. 电源世界, 2008(4): 63–65.
YAN Xiaojin, PAN Yan, CHEN Yongzhen. Basic requires of electrolytic capacitor performance by SMPS[J]. The World of Power Supply, 2008(4): 63–65. (in Chinese) |
| [4] | Heinz V D B, Georg S, Matthias W.Power driver topologies and control schemes for LEDs[C]//Proceedings of the 2007 Twenty Second Annual IEEE Applied Power Electronics Conference, February 25-March 1, 2007, Anaheim, CA, USA.Piscataway:IEEE Press, 2007:1319-1325. |
| [5] |
裴倩, 王正仕, 陈辉明.
大功率LED驱动电源对光效的影响研究[J]. 电力电子技术, 2010, 44(3): 55–56.
PEI Qian, WANG Zhengshi, CHEN Huiming. Luminous efficiency of ripple current power driving high power LED[J]. Power Electronics, 2010, 44(3): 55–56. (in Chinese) |
| [6] | Zhou J M, Yan W. Experimental investigation on the performance characteristics of white LEDs used in illumination application[C]//Proceedings of the 2007 IEEE Power Electronics Specialists Conference, June 17-21, 2007, Orlando, FL. Piscataway:IEEE Press, 2007:1436-1440. |
| [7] | Han L, Narendran N. An accelerated test method for predicting the useful life of an LED driver[J]. IEEE Transactions on Power Electronics, 2011, 26(8): 2249–2257. DOI:10.1109/TPEL.2010.2095885 |
| [8] | 沈海平. 大功率LED可靠性预测机制研究[D]. 杭州: 浙江大学博士学位论文, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10335-2008084012.htm |
| [9] | Meneghini M, Trevisanello L R, Meneghesso G, et al. A review on the reliability of gan-based LEDs[J]. IEEE Transactions on Device and Materials Reliability, 2008, 8(2): 323–331. DOI:10.1109/TDMR.2008.921527 |
| [10] | Pang H M, Bryan P M H. A life prediction scheme for electrolytic capacitors in power converters without current sensor[C]//Proceedings of the 2010 Twenty-Fifth Annual IEEE Applied Power Electronics Conference and Exposition, February 21-25, 2010, Palm Springs, CA. Piscataway:IEEE Press, 2010:973-979. |
| [11] | Qin Y X, Chung H S H, Lin D Y, et al. Current source ballast for high power lighting emitting diodes without electrolytic capacitor[C]//Proceedings of the 34th Annual Conference of IEEE Industrial Electronics, November 10-13, 2008, Orlando, FL.Piscataway:IEEE Press, 2008:1968-1973. |
| [12] | Gu L L, Ruan X B, Xu M, et al. Means of eliminating electrolytic capacitor in AC/DC power supplies for LED lightings[J]. IEEE Transactions on Power Electronics, 2009, 24(5): 1399–1408. DOI:10.1109/TPEL.2009.2016662 |
| [13] | Tang Z D, Wang G T, Xie X H, et al.White LED power supply based on buck converter with active ripple compensation[C]//Proceedings of the 2011 International Conference on Consumer Electronics, Communications and Networks, April 16-18, 2011, Xianning, Hubei, China. Piscataway:IEEE Press, 2011:943-946. |
| [14] |
唐治德, 王官涛, 杨红, 等.
一种新颖的BUCK型LED驱动电路[J]. 电气应用, 2011, 30(6): 45–48.
TANG Zhide, WANG Guantao, YANG Hong, et al. A novel buck circuit for LED[J]. Electrotechnical Application, 2011, 30(6): 45–48. (in Chinese) |
| [15] | Dallago E, Passoni M, Sassone G. Lossless current sensing in low-voltage high-current DC/DC modular supplies[J]. IEEE Transactions on Industrial Electronics, 2000, 47(6): 1249–1252. DOI:10.1109/41.887952 |
| [16] | Erickson R W, Maksimovic D. Fundamentals of power electronics[M]. 2nd ed. New York: Kluwer Academic Publishers, 2004. |
| [17] |
吴国营, 张波.
电流模式变换器的完整小信号模型及环路补偿[J]. 电工技术学报, 2008, 23(10): 83–87.
WU Guoying, ZHANG Bo. Whole small signal model and compensation for regulators with current programmed mode[J]. Transactions of China Electrotechnical Society, 2008, 23(10): 83–87. DOI:10.3321/j.issn:1000-6753.2008.10.015 (in Chinese) |
| [18] |
杨明.
电感电流连续状态BUCK变换器的小信号分析[J]. 舰船电子对抗, 2007, 30(2): 72–75, 78.
YANG Ming. Small signal analysis of BUCK converter in the state of continuous inductance current[J]. Shipboard Electronic Countermeasure, 2007, 30(2): 72–75, 78. (in Chinese) |
 2013, Vol. 36
2013, Vol. 36

