1b. 重庆大学新型微纳器件与系统技术国防重点学科实验室, 重庆 400044;
2. 清华大学 精密测试技术及仪器国家重点实验室, 北京 100084;
3. 深圳清华大学研究院, 深圳 518057
1b. National Key Laboratory of Fundamental Science of Micro/Nano-Device and System Technology, Chongqing University, Chongqing 400044, China;
2. State Key Laboratory of Precision Measurement Technology and Instruments, Tsinghua University, Beijing 100084, China;
3. Research Institute of Tsinghua University in Shenzhen, Shenzhen, Guangdong 518057, China
近年来,辉光放电等离子体的应用越来越广泛。在灭菌、等离子体喷涂、材料表面改性、薄膜沉积、离子源、等离子体显示、飞行器等离子体隐形、废弃物处理等领域得到了广泛的应用。通常辉光放电要在低气压下产生,这就需要有复杂的真空系统来维持放电环境。一方面增加了成本,另一方面增大了体积,使其在便携式仪器上的应用受到了很多限制。但大气压辉光放电在放电过程中容易向火花过渡,导致在大气压下产生稳定的辉光放电非常困难。
介质阻挡放电是一种可在大气压下实现辉光放电的方法。早期的研究者如Okazaki等人[1],报道了在惰性气体环境等条件下实现介质阻挡辉光放电。之后研究者不断增多,如Garamoon等人[2]用50 Hz高压交流电实现空气介质阻挡辉光放电,Massines等人[3]研究了不同气压下介质阻挡辉光放电的情况,清华大学王新新课题组[4]对大气压氮气、氖气介质阻挡辉光放电进行了研究,南京工业大学方志课题组[5]对大气压下氖气、氦气介质阻挡辉光放电的不同特性进行深入研究,大连理工大学李寿哲等人[6]实现了大气压射频辉光放电。
除上述方法外,由极不对称结构产生直流大气压辉光放电也是一种方法,如针-板结构。由于可以采用直流电源,降低了电源成本,减少了匹配电路,在应用中具有优势,因此引起了部分学者的关注,开展了相关研究。如Akishev教授课题组利用针-板直流电晕放电来获取稳定的大气压辉光放电,并将其应用于棉布的表面改性等方面[7-9]。在此基础上,大连理工大学的任春生教授课题组[10-11]实现了多针电晕增强大气压辉光放电。在这些研究及应用中,电极间的间隙一般在10 mm左右。间隙较大,电极间的击穿电压较高,可以有效地防止放电向火花过渡。但是,这也使得整个放电装置体积变大,放电电压较高,不利于在便携式仪器中应用。如能减小放电间隙,不仅仅可以缩小放电装置的体积还能降低放电电压,降低对电源的要求,在便携式仪器中有较大的优势。
笔者提出了一种可用于离子源的线-筒型大气压辉光放电装置,放电间隙仅为1.92 mm,大大缩减了整个放电装置的体积,放电起始电压仅在-4 kV左右,可实现稳定的辉光放电。为了更好地利用产生的等离子体,笔者分析了振动温度、转动温度的计算方法,并结合光谱实验数据计算了它的振动温度和转动温度。将该装置作为离子源应用于敞开式质谱中,进行了质谱分析实验,得到了较好的结果。
1 实验装置图 1所示为线-筒型大气压辉光放电装置的示意图。主要由内线电极、外筒电极组成,线电极为一根直径0.16 mm表面光滑的不锈钢圆柱,筒电极是一个中空的紫铜圆柱,其内直径为4 mm。位于筒壁电极上的4个对称槽的作用是通入气体和牵引离子。实验中采用0~-5 kV直流电压源供电。氮气及需要电离的物质通过玻璃管导入。当电压足够高时,内外电极之间发生放电。为了获取放电电流信号,如图 1所示,在外电极一端串联一个采样电阻,并通过Tektronix TDS1001B示波器进行观察。施加的高压直流电压通过Tektronix P6015A高压探头衰减1 000倍后输入示波器。放电发出的光谱通过Acton Spectrapro 2500i光谱仪进行测量。
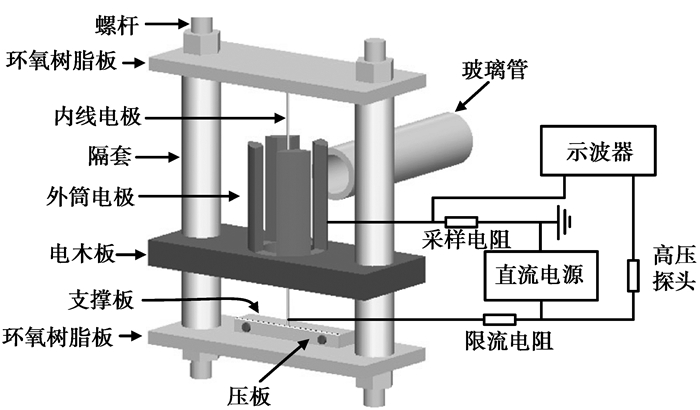
|
图 1 装置结构及实验电路示意图 |
该装置放电间隙很小,为了获得一致的放电需要保证有较高的同轴度。笔者采用的装置如图 1所示,使用环氧树脂、铝等机械性能好,随温度和湿度变化较小的材料。通过精密加工和装配,可以保证内外电极具有较高的同轴度[12]。
2 实验与分析图 2所示为放电电压和电流波形图。从图中可以看出,当施加电压达到-3.5 kV时,产生电晕放电,如图 2(a)所示为典型的特里切里脉冲。当电压升高时,放电愈加剧烈,放电电流频率增加。图 2(b)所示为电压-4 kV时的放电电流波形。如图 2(c)所示,当电压达到-4.4 kV时放电开始向辉光过渡,放电电流中包含了直流分量。继续增大电压至-4.5 kV时,如图 2(d)所示放电进入辉光状态,放电电流为直流。图 3所示为施加电压为-4.5 kV,辉光放电状态时的照片,从照片看无放电细丝的存在。
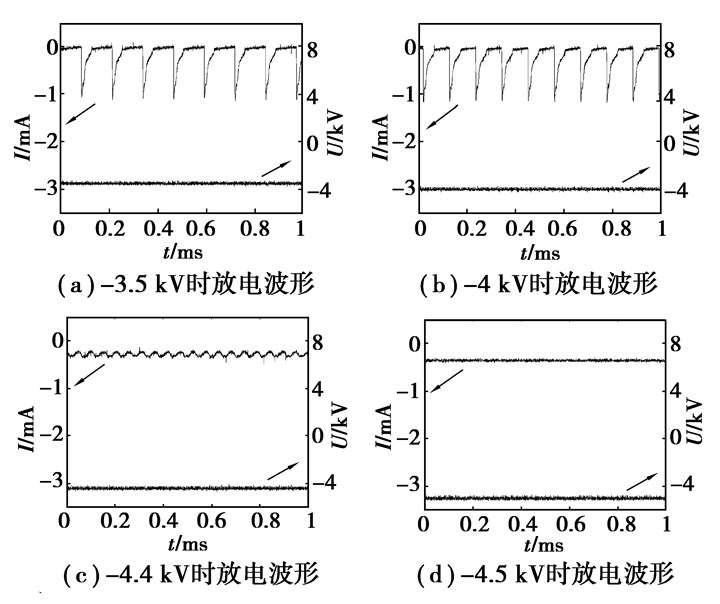
|
图 2 放电电压电流波形图 |

|
图 3 放电照片 |
在筒电极附近电场强度较小,放电产生的电子在该区域能量较小,会被周围的氧气吸附,形成氧负离子。由于该区域的电场强度较低,氧负离子的运动速率较低,从而会引起聚集,形成反向电场。当氧负离子形成的反向电场强度足够高而使合场强低于放电所需电场时,放电便会停止。停止后,电场将氧负离子迁移走,当合场强足够高时,下次放电得以发生。这就是实验中出现特里切里脉冲的原因。若电场足够大,则氧负离子的运动速率相应提高,以至于无法聚集,也就不会出现放电熄灭的现象,电流脉冲随之消失,成为直流,进入辉光状态。
为了确定产生等离子体的振动温度和转动温度等参数,用光谱仪(Acton Spectrapro 2500i)采集了该等离子体的发射光谱。在施加电压为-4.5 kV时的光谱图如图 4所示。
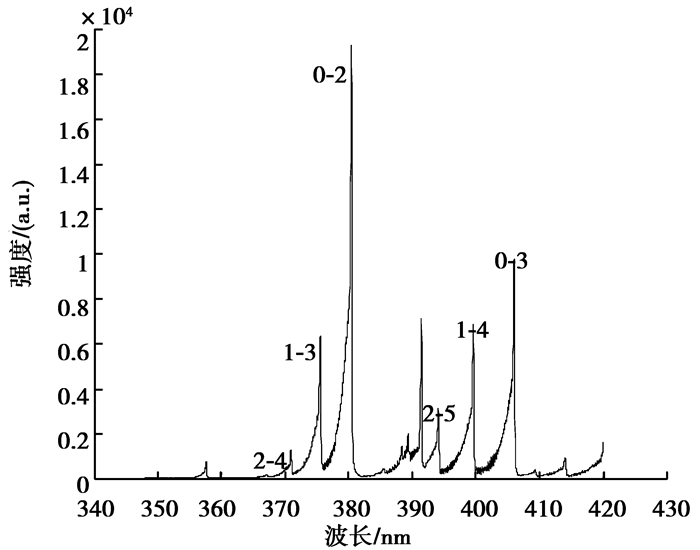
|
图 4 实验采集光谱图 |
振动温度是等离子体的重要参数之一,为了能计算振动温度,下面推导了利用氮气第二正带系(c3Πu→B3Πg)计算振动温度的方法。
理论上,氮气作为双原子分子,其发射光谱中的谱带强度可以用下式[13-19]表示:
| $ {I_{v'v''}} = hc{\upsilon _{v'v''}}{A_{v'v''}}{N_{v'}}, $ | (1) |
其中:h为普朗克常量;c为光速;v′为上态振动量子数;v″为下态振动量子数;υv′v″为跃迁过程中发射的光量子的波数;Av′v″为跃迁几率;Nv′为上态分子数。
分子振动能级的振动能量[19]可表示为
| $ \begin{array}{*{20}{c}} {{E_{v'}} = {\omega _e}\left[ {v' + \frac{1}{2}} \right] - {\omega _e}{x_e}{{\left[ {v' + \frac{1}{2}} \right]}^2} + }\\ {{\omega _e}{y_e}{{\left[ {v' + \frac{1}{2}} \right]}^3} + \cdots ,} \end{array} $ | (2) |
其中,对氮分子ωe=2 035.1 cm-1和ωexe=17.08 cm-1,第三项及其后面项可忽略不计[19]。
在局部热平衡条件下,上态分子数分布满足玻尔兹曼分布[17],可表示如下:
| $ {N_{v'}} = {N_0}{{\rm{e}}^{ - {E_{v'}}/k{T_v}}}, $ | (3) |
由式(1)可推导出:
| $ {N_{v'}} = {I_{v'v''}}/hc{v_{v'v''}}{A_{v'v''}}, $ | (4) |
联合式(3)和式(4)可得:
| $ {I_{v'v''}}/{v_{v'v''}}{A_{v'v''}} = hc{N_0}{e^{ - {E_{v'}}/k{T_v}}}, $ | (5) |
将式(5)取自然对数,可得:
| $ {\rm{ln}}\left( {{I_{v'v''}}/{v_{v'v''}}{A_{v'v''}}} \right) = \ln hc{N_0} - {E_{v'}}/k{T_v}。$ | (6) |
在式(6)中,υv′v″、Av′v″、lnhcN0以及k为常数,令lnhcN0=a,Iv′v″/υv′v″Av′v″=X,则式(6)可简化为
| $ \ln X = a - {E_{v'}}/k{T_v}。$ | (7) |
因此可以以lnX为纵坐标,Ev′为横坐标,对所测的数据进行拟合。得到拟合直线负斜率的倒数就是kTv,从而计算出振动温度Tv。
由于本实验中含有大量的氮气,因此该方法适用于本实验。利用图 4中测得的氮气第二顺序带组Δv=(0-2, 1-3, 2-4)和第三顺序带组Δv=(0-3, 1-4, 2-5)可得出振动温度的拟合曲线,如图 5所示。从而求得该等离子体的振动温度约为2 360 K,计算中所需的参数如表 1所示。
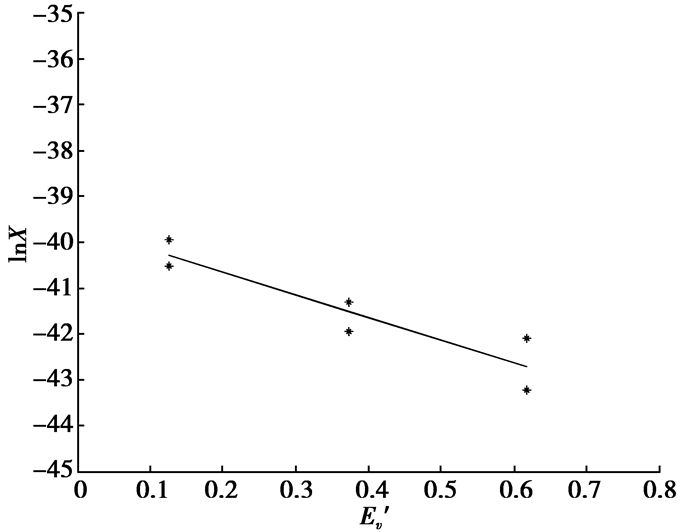
|
图 5 振动温度计算曲线 |
| 表 1 振动温度计算所需参数 |
转动温度作为等离子体的另外一个重要参数,也具有重要的意义。在大气压情况下,气体密度很高,一般认为转动温度与气体温度近似相等。而气体温度则影响着该等离子体的应用领域。
通过计算机谱线拟合来计算等离子体转动温度是一种非常有效的方法,其关键是能够计算模拟出光谱的形状。笔者给出了该计算的方法原理,并对该等离子体的转动温度进行了计算。
发射谱线强度
Av′v″是自发发射的爱因斯坦跃迁几率。按照波动力学,当简并度为dn的简并能级之间发生跃迁时,它与这个跃迁的矩阵元有如下关系[13]:
| $ {A_{v'v''}} = \frac{{64{{\rm{ \mathit{ π} }}^4}\upsilon _{nm}^3}}{{3h}}\frac{{\sum {{{\left| {{R^{{n_i}{m_k}}}} \right|}^2}} }}{{{d_n}}}。$ | (8) |
转动态中的实际分子数目Nv′[13]可以表示为
| $ {N_{v'}} = \frac{N}{{{Q_r}}}\left( {2J + 1} \right){{\rm{e}}^{ - BJ\left( {J + 1} \right)hc/kT}} $ | (9) |
其中Qr为转动态和,可表示为Qr=1+3e-2Bhc/kT+5e-6Bhc/kT+…。
令dn=2J+1,则联合式(1)、(8)、(9),可计算出
| $ \begin{array}{l} I_{发射}^{nm} = \frac{N}{{{Q_r}}}\left( {2J + 1} \right)hc{\upsilon _{nm}}\frac{{64{{\rm{ \mathit{ π} }}^4}\upsilon _{nm}^3}}{{3h}}\frac{{\sum {{{\left| {{R^{{n_i}{m_k}}}} \right|}^2}} }}{{{d_n}}}{{\rm{e}}^{ - BJ\left( {J + 1} \right)hc/kT}} = \\ \;\;\;\;\;\frac{{64{{\rm{ \mathit{ π} }}^4}\upsilon _{nm}^4cN}}{{3{Q_r}}}\left( {\sum {{{\left| {{R^{{n_i}{m_k}}}} \right|}^2}} } \right){{\rm{e}}^{ - BJ\left( {J + 1} \right)hc/kT}} = \\ \;\;\;\;\;\frac{{2{C_{发}}\upsilon _{nm}^4}}{{{Q_r}}}{S_J}{{\rm{e}}^{ - BJ\left( {J + 1} \right)hc/kT}}。\end{array} $ | (10) |
其中,C发为常数,SJ对于P、Q、R三支可以分别定义[21]为
| $ S_J^P = 6J\left( {J + 1} \right) - 10/\left( {J + 1} \right), $ | (11) |
| $ S_J^Q = 10/J + 10/\left( {J + 1} \right), $ | (12) |
| $ S_J^R = 6J - 10/J。$ | (13) |
对于P、Q、R三支的波数υnm可以定义[13]为
| $ \upsilon _{nm}^P = {\upsilon _0} - \left( {B' + B''} \right)J + \left( {B' - B''} \right){J^2}, $ | (14) |
| $ \upsilon _{nm}^Q = {\upsilon _0} + \left( {B' - B''} \right)J + \left( {B' - B''} \right){J^2}, $ | (15) |
| $ \upsilon _{nm}^R = {\upsilon _0} + 2B' + \left( {3B' - B''} \right)J + \left( {B' - B''} \right){J^2}。$ | (16) |
这样通过式(10)~(16)就可以计算出在某一波长点上的P、Q、R三支对应谱线的强度Ip(i)、IQ(i)、IR(i)。
此时计算得到的Ip(i)、IQ(i)、IR(i)为理论计算值,为了能够得到与仪器参数相吻合的谱线强度,必须将理论计算值进行谱线线型展宽。在实际应用中,往往采用高斯线型G(ω)与洛伦兹线型Г(ω)的叠加。两种线型所占的比重由采用的光谱仪参数确定。展宽后将P、Q、R三支对应谱线的强度相加便可得到总的谱线强度Isum。
图 6所示为利用笔者推导的计算方法编程求解而得到的谱线拟合结果,可以看出谱线拟合的效果良好,说明了该方法的有效性。图 6中采集光谱的条件为施加电压-4.5 kV,辉光放电。通过拟合计算得到转动温度约为830 K。
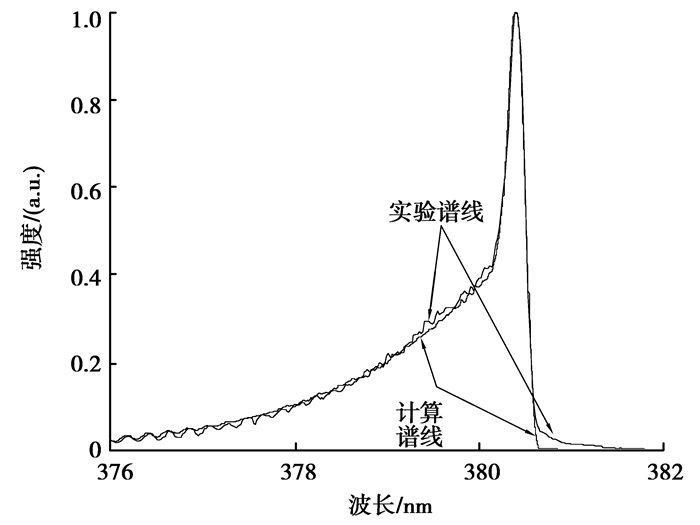
|
图 6 光谱拟合结果 |
该放电装置已被用于敞开式质谱离子源中。图 7所示是电离乙酸的结果,图中质荷比为59的谱峰是乙酸离子,质荷比为119的谱峰是乙酸的二聚物离子。通过实验发现,该离子源可以很好地离子化甲酸、乙酸、苯酚等化学物质。更进一步的研究正在进行中,将在后续文章中报道。
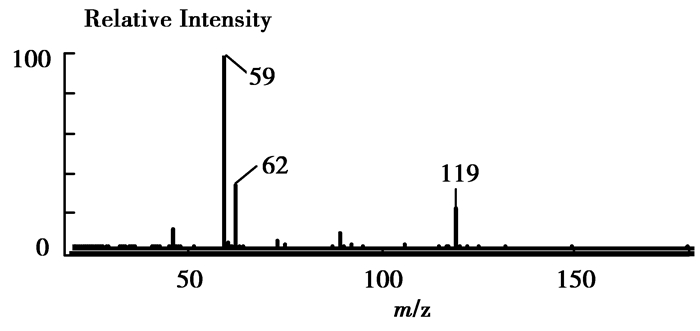
|
图 7 乙酸质谱图 |
笔者介绍了一种线-筒型直流大气压辉光放电装置。通过实验发现,其放电特性与低气压下辉光放电的特性基本一致。详细推导了振动温度和转动温度的计算方法,并计算了该等离子体的振动温度和转动温度。在施加电压为-4.5 kV时,振动温度为2 360 K,转动温度为830 K。并将该装置应用于敞开式质谱仪的离子源,进行了质谱实验,得到了良好的效果。
| [1] | Kanazawa M, Kogoma M, Moriwaki T, et al. Stable glow plasma at atmospheric pressure[J]. Journal of Physics D:Applied Physics, 1988, 21(5): 838–840. DOI:10.1088/0022-3727/21/5/028 |
| [2] | Garamoon A A, EL-Zeer D M. Atmospheric pressure glow discharge plasma in air at frequency 50 Hz[J]. Plasma Sources Science and Technology, 2009, 18(4): 045006. DOI:10.1088/0963-0252/18/4/045006 |
| [3] | Massines F, Gheradi N, Naudé N, et al. Glow and townsend dielectric barrier discharge in various atmosphere[J]. Plasma Physics and Controlled Fusion, 2005, 47(12B): B577–B588. DOI:10.1088/0741-3335/47/12B/S42 |
| [4] |
王新新, 李成榕.
大气压氮气介质阻挡均匀放电[J]. 高电压技术, 2011, 37(6): 1405–1415.
WANG Xinxin, LI Chengrong. Review of homogenous dielectric barrier discharge in nitrogen at atmospheric pressure[J]. High Voltage Engineering, 2011, 37(6): 1405–1415. (in Chinese) |
| [5] |
方志, 蔡玲玲, 雷枭.
氦气和氖气中大气压均匀介质阻挡放电特性比较[J]. 高电压技术, 2011, 37(7): 1766–1774.
FANG Zhi, CAI Lingling, LEI Xiao. Comparison of the discharge characteristics of homogeneous dielectric barrier discharge in He and Ne[J]. High Voltage Engineering, 2011, 37(7): 1766–1774. (in Chinese) |
| [6] | Li S Z, Wu Q, Zhang J L, et al. Development of an atmospheric-pressure homogeneous and cold Ar/O2 plasma source operating in glow discharge[J]. Physics of Plasmas, 2010, 17(6): 063506.1–063506.5. |
| [7] | Akishev Y, Grushin M, Kochetov I, et al. Negative corona, glow and spark discharges in ambient air and transitions between them[J]. Plasma Sources Scicence and Technology, 2005, 14(2): S18–S25. DOI:10.1088/0963-0252/14/2/S03 |
| [8] | Leys C, Neirynck D, Morent R, et al. DC-excited cold atmospheric pressure plasmas[J]. Czechoslovak Journal of Physics, 2006, 56(Sup2): B896–B902. |
| [9] | Temmerman E, Leys C. Surface modification of cotton yarn with a DC glow discharge in ambient air[J]. Surface and Coatings Technology, 2005, 200(1/2/3/4): 686–689. |
| [10] | Ren C S, Ma T C, Wang D Z, et al. A study of cross-gas-flow to stabilize an atmospheric pressure glow plasma in a multi-pin-to-multi-cupped-plane negative corona discharge[J]. Journal of Electrostatics, 2006, 64(1): 23–28. DOI:10.1016/j.elstat.2005.05.001 |
| [11] |
齐冰, 任春生, 马腾才, 等.
多针电晕增强大气压辉光放电稳定性研究[J]. 物理学报, 2006, 55(1): 331–336.
QI Bing, REN Chunsheng, MA Tengcai, et al. Stabilization of the multi-pin to multi-sphere plane negative corona discharge[J]. Acta Physica Sinica, 2006, 55(1): 331–336. (in Chinese) |
| [12] |
刘坤, 唐飞, 王晓浩, 等.
一种用于高场非对称波形离子迁移谱系统的新型敞开式化学离子源[J]. 物理化学学报, 2009, 25(8): 1662–1670.
LIU Kun, TANG Fei, WANG Xiaohao, et al. Novel chemical ion source for a high-field asymmetric waveform ion mobility spectrometer used under ambient conditions[J]. Acta Physico-Chimica Sinica, 2009, 25(8): 1662–1670. (in Chinese) |
| [13] | 赫兹堡. 分子光谱与分子结构:第一卷[M]. 北京: 科学出版社, 1983. |
| [14] |
刘峰, 董丽芳, 李树锋, 等.
氩气/空气介质阻挡放电中分子振动温度研究[J]. 河北大学学报:自然科学版, 2005, 25(6): 595–598.
LIU Feng, DONG Lifang, LI Shufeng, et al. Molecular vibrational temperature in Ar/Air dielectric barrier discharge[J]. Journal of Hebei University:Natural Science Edition, 2005, 25(6): 595–598. (in Chinese) |
| [15] |
董丽芳, 齐玉妍, 高瑞玲, 等.
中等pd值介质阻挡放电中等离子体温度研究[J]. 光谱学与光谱分析, 2007, 27(11): 2175–2177.
DONG Lifang, QI Yuyan, GAO Ruiling, et al. Study on plasma temperature in dielectric barrier discharge at the middle value of pd[J]. Spectroscopy and Spectral Analysis, 2007, 27(11): 2175–2177. (in Chinese) |
| [16] |
齐玉妍, 董丽芳, 赵增超.
介质阻挡放电中不同斑图的微放电通道中分子振动温度研究[J]. 河北大学学报:自然科学版, 2007, 27(Sup): 204–207.
QI Yuyan, DONG Lifang, ZHAO Zengchao. Investigation of molecular vibrational temperature of individual microdischarge channel in patterns in dielectric barrier discharge[J]. Journal of Hebei University; Natural Science Edition, 2007, 27(Sup): 204–207. (in Chinese) |
| [17] | 刘锋. 介质阻挡放电电子激发温度、分子振动温度研究[D]. 河北: 河北大学, 2006. http://cdmd.cnki.com.cn/article/cdmd-10075-2006071774.htm |
| [18] | 张家良. 低温等离子体发射光谱学研究[D]. 大连: 大连理工大学, 2002. http://cdmd.cnki.com.cn/Article/CDMD-10141-2003060756.htm |
| [19] |
董丽芳, 刘峰, 李树锋, 等.
大气压氩气/空气介质阻挡放电中分子振动温度[J]. 光谱学与光谱分析, 2006, 26(5): 802–804.
DONG Lifang, LIU Feng, LI Shufeng, et al. Measurement of molecular vibrational temperature in dielectric barrier discharge in argon/air at atmospheric pressure[J]. Spectroscopy and Spectral Analysis, 2006, 26(5): 802–804. (in Chinese) |
| [20] |
董丽芳, 李永辉, 陈文军, 等.
空气介质阻挡放电中氮分子离子的转动温度研究[J]. 光谱学与光谱分析, 2007, 27(12): 2406–2408.
DONG Lifang, LI Yonghui, CHEN Wenjun, et al. Measurement of N2+ rotational temperature in air dielectric barrier discharge[J]. Spectroscopy and Spectral Analysis, 2007, 27(12): 2406–2408. (in Chinese) |
| [21] | Phillips D M. Determination of gas temperature from unresolved bands in the spectrum from a nitrogen discharge[J]. Journal of Physics D:Applied Physics, 1975, 9(3): 507–521. |
 2013, Vol. 36
2013, Vol. 36


