磁感应成像技术(magnetic induction tomography, MIT)是一种非接触式测量生物组织电导率的成像技术[1]。MIT的理论基础是法拉第电磁感应定理,基本原理是通过正弦电流的激励线圈产生主磁场B,将被测物体置于主磁场B场中,物体内部诱导出涡流电流,将产生二次磁场ΔB引起空间中磁场分布的变化, 在检测线圈上检测到B+ΔB,当物体的电导率发生改变,内部的涡流电流分布将随之改变,从而检测线圈的电压也发生变化,检测线圈电压的变化与电导率分布存在密切的关系,利用重构算法可以实现对被测物体内部电导率分布的图像显示[2-3]。由于激励和检测均在被测物体外部进行,MIT是一种非接触,无创的电阻抗成像技术,这一特点在生物医学无创检测成像领域有很好的应用前景[4]。
MIT在医学领域无创检测,国内外的研究学者对MIT逆问题进行了大量的研究。Konjenevsky首先将EIT的滤波反投影方法运用于磁感应成像重构算法[5]。Mortarelli突破Geselowitz的适用条件,扩展了Geselowitz关系,导出了适用于任何频率的正弦交变电流源的灵敏度矩阵公式,Watson[6]和Scharfetter[7-8]利用扩展的Geselowitz关系构造灵敏度矩阵,进行磁感应图像重建。Merwa[9-10]和Vauhkonen[11]采用正则化算法重构磁感应的电导率分布。国内研究人员王聪[12]采用修正的Newton Raphson(NR)算法成功地进行了仿真图像重建。柯丽[13]运用滤波反投影算法重建电导率分布图像。王旭的研究小组用Tikhonov正则化算法对解的适定性产生初步的成像区域, 之后再利用变差正则化算法对解的保边缘性和锐化作用进行图像重建[14]。
Konjenevsky的算法对灵敏度的假设适用于高电导率的目标,不适用于低电导率的生物组织。灵敏度矩阵和正则化算法求解逆问题,有较好的精度,但是计算量庞大以及重构时间长[15],不适于动态连续监护。笔者结合国内外研究现状,针对这种正弦均匀磁场激励MIT系统的模型,采用滤波反投影重构图像。该文中针对MIT的滤波反投影(filtered back-projection algorithm, FBP)进行了以下研究:1)基于滤波反投影算法MIT系统的模型研究。2)针对磁力线弯曲特性,引入亥姆霍兹线圈做激励系统,同时加入窗口滤波器基本减少了涡流磁场发散对周围线圈的影响。
1 激励系统和MIT系统的模型 1.1 亥姆霍兹线圈激励系统在传统的MIT测量系统中,激励磁场产生都是采用单个线圈注入电流的方式,其中有以下缺点:由于激励磁场分布不均匀,在计算逆问题时,需要对激励磁场加复杂的权重,运算更复杂,耗时多;激励磁场的深度比较浅,方向不一致。
笔者基于克服上述的缺点,寻找一种正弦均匀激励磁场,为MIT系统提供良好的激励,而亥姆霍兹线圈就可以产生一组磁场均匀,深度较深的磁场。
亥姆霍兹线圈的基本结构:一对半径都为R圆形线圈,并且同轴放置,其间距2Z0等于半径R。根据轴对称线圈磁场计算,在两线圈同轴方向上BZ的表达式[16]为
| $ \begin{array}{l} {B_z} = {B_1}z + {B_2}z\\ \;\;\;\; = \frac{{{\mu _0}I}}{{2R}}{\left( {\frac{{{\gamma _1}}}{{2\alpha }}} \right)^{\frac{3}{2}}} \times \left[ {A\left( {{\gamma _1}} \right) + \alpha B\left( {{\gamma _1}} \right)} \right] + \\ \;\;\;\;\;\;\;\frac{{{\mu _0}I}}{{2R}}{\left( {\frac{{{\gamma _2}}}{{2\alpha }}} \right)^{\frac{3}{2}}} \times \left[ {A\left( {{\gamma _2}} \right) + \alpha B\left( {{\gamma _2}} \right)} \right], \end{array} $ | (1) |
其中:
| $ \begin{array}{l} \alpha {\rm{ = }}\frac{y}{R},\;\beta = \frac{{{z_0} \pm z}}{R},\;\gamma = \frac{{2yR}}{{{{\left( {{z_0} \pm z} \right)}^2} + {y^2} + {R^2}}},\\ A\left( \gamma \right){\rm{ = }}\frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_0^{2{\rm{ \mathsf{ π} }}} {{{\left( {1 - \gamma \cos \cos \theta } \right)}^{ - \frac{3}{2}}}{\rm{d}}\theta } ,\\ B\left( \gamma \right){\rm{ = }}\frac{1}{{2{\rm{ \mathsf{ π} }}}}\int_0^{2{\rm{ \mathsf{ π} }}} {\cos \cos \theta {{\left( {1 - \gamma \cos \cos \theta } \right)}^{ - \frac{3}{2}}}{\rm{d}}\theta } 。\end{array} $ |
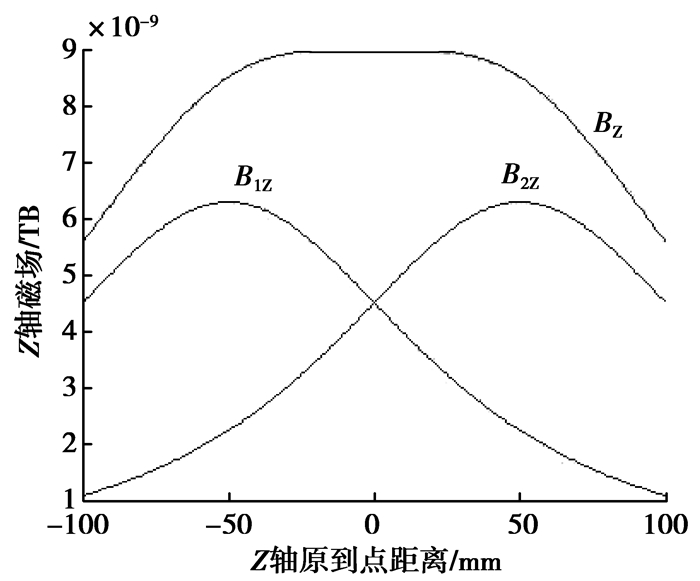
对式(1)用Matlab对Z轴磁场公式进行计算得到图 1。
|
图 1 Z轴磁场分量 |
从图 1可以看出,亥姆霍兹线圈Z轴上(-50~50 mm),BZ近似均匀磁场。
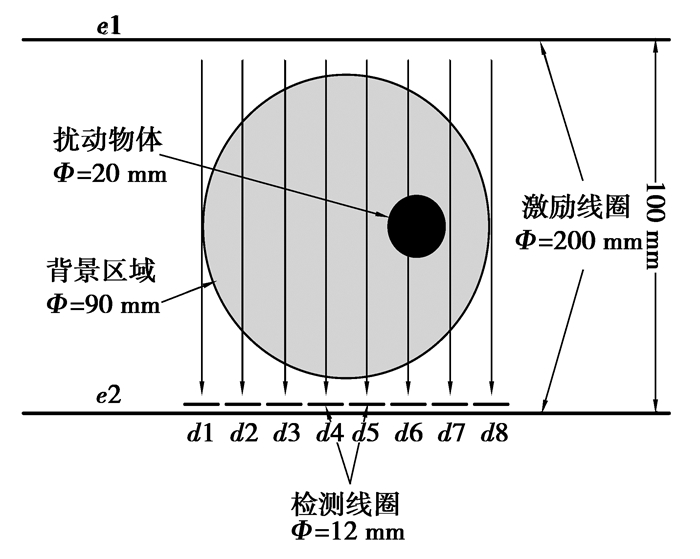
1.2 MIT系统的模型基于亥姆霍兹线圈激励的MIT实验模型如图 2所示。模型主要由1个圆形背景区域,1个圆形扰动物体,1组亥姆霍兹线圈(e1,e2)和8个检测线圈(d1~d8)构成。亥姆霍兹线圈的直径200 mm,2个亥姆霍兹线圈的间距100 mm,检测线圈直径12 mm,每个线圈相距1 mm,8个检测线圈位于其中一个激励线圈同侧,到激励线圈的距离2 mm,其中检测线圈轴线和激励线圈轴线在同一平面上。背景区域直径90 mm,扰动物体直径20 mm,其高度40 mm。
|
图 2 MIT系统模型 |
FBP实际上是在反投影的基础上先进行卷积运算。滤波反投影重建图像的具体过程:先把由检测器上获得的原始数据与一个滤波函数进行卷积运算,得到各方向卷积的投影函数;然后再把它们从各方向进行反投影,即按其原路径平均分配到每一剖分单元上,进行叠加后得到每一剖分单元的值;再经过适当处理后就可以得到被扫描物体的断层图像[17]。
FBP算法是在傅里叶中心切片定理的基础上发展起来的。在中心切片定理的基础上可以推导出滤波反投影算法的连续形式如下:
| $ f\left( {x,y} \right) = \int_0^{\rm{ \mathsf{ π} }} {q\left( {s,\theta } \right){\rm{d}}\theta } , $ | (2) |
| $ q\left( {s,\theta } \right) = p\left( {s,\theta } \right) \times h\left( s \right), $ | (3) |
其中,
| $ \begin{array}{l} s = x\cos \theta + y\sin \theta ,\\ h\left( s \right) = \int_{ - \infty }^{ + \infty } {\left| w \right|{{\rm{e}}^{i2{\rm{ \mathsf{ π} }}ws}}{\rm{d}}s} 。\end{array} $ |
其中:p(s, θ)为某角度下投影数据; q(s, θ)为滤波器滤波后的滤波投影。
2.2 磁感应成像滤波反投影原理在CT成像中,由于透光率与经过该点的射线投影之和(即某点的密度值)呈正比,并且被测物密度异常区域的位置变化与透光率无关,因此在CT成像技术中应用反投影算法来实现图像重构。
MIT成像与CT成像的类似点如下:当激励电流的大小、频率,以及线圈位置不变的情况下,检测线圈的感应电压与被测物的电导率成正比。这与CT成像技术的基本原理类似。
MIT成像与CT成像不同之处在于:①CT中成像路径是沿X射线的直线,而磁力线路径是弯曲的。②CT成像中,在一条路径上电导率异常区域的位置不同对光的吸收率没有影响;但是在MIT成像技术中,物体位置的不同对检测线圈的感应电压有很大的影响。
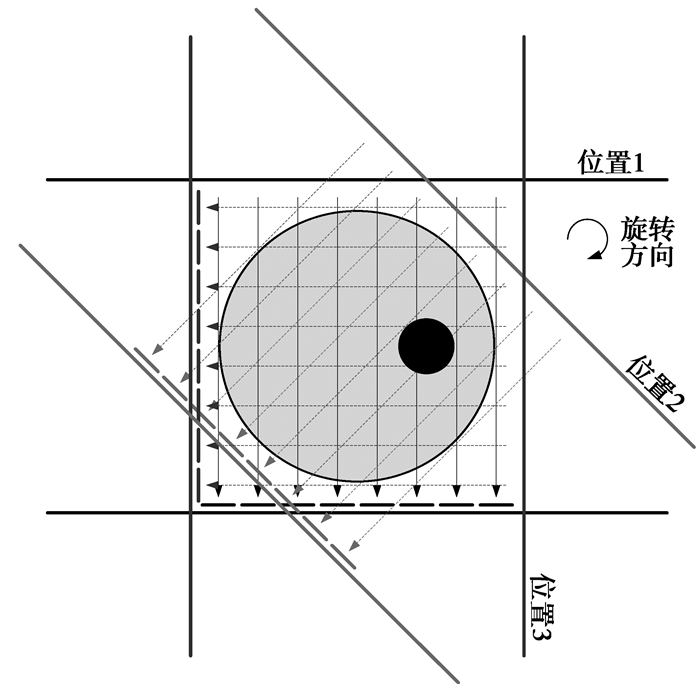
针对上述两点差别提出以下解决方法。首先引入亥姆霍兹线圈做激励系统,产生的主激励磁场可视为均匀磁场,方向近似为直线,同时加入窗口滤波器减少了涡流磁场发散对周围线圈的影响,这就基本解决了成像路径是曲线的问题。通过对路径加权可以消除物体到检测线圈距离对感应电压的影响。其基本测量原理如图 3所示。
|
图 3 磁感应成像反投影原理图 |
如图 3所示,每组测量m个检测的感应电压Um(m为检测线圈个数)。再将检测系统在观察平面以中心为中心旋转一定角度Δϕ,如图中由位置1旋转到位置2。得到另一组电压数据,如此重复,直至旋转N次,使NΔϕ=360°为止。即得到m×n维的电压值矩阵。
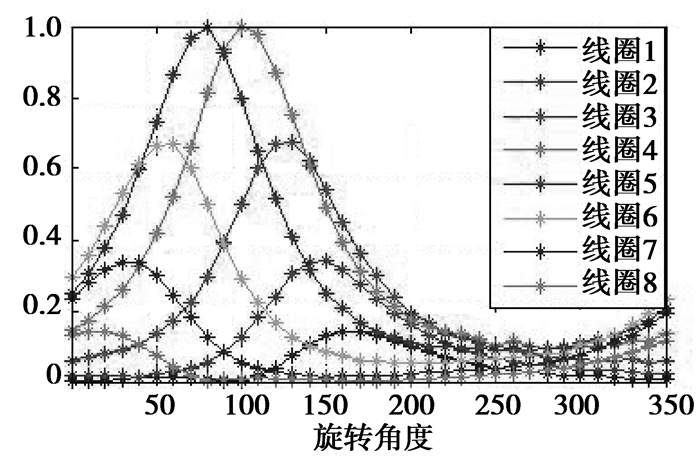
3 实验仿真 3.1 模型仿真参照图 2模型的数据建立仿真模型,用Ansoft Maxwell电磁软件仿真。激励线圈通过50 mA的10 MHz正弦电流,在亥姆霍兹线圈腔内产生较均匀和近似直线的激励磁场。扰动物体的电导率设置为1 s/m, 背景区域电导率为0.2 s/m。检测和激励系统以步进10°旋转一周,得到36×8个电压数据。将扰动物体电导率和背景区域电导率都设置为0.2 s/m,其检测电压数据作为基准数据,将36×8的仿真数据和基准数据做差值,并归一化,8个检测线圈的数据如图 4所示,波峰位置表示扰动物体对应位置,可以明显发现随着系统的旋转,波峰在移动。
|
图 4 仿真数据 |
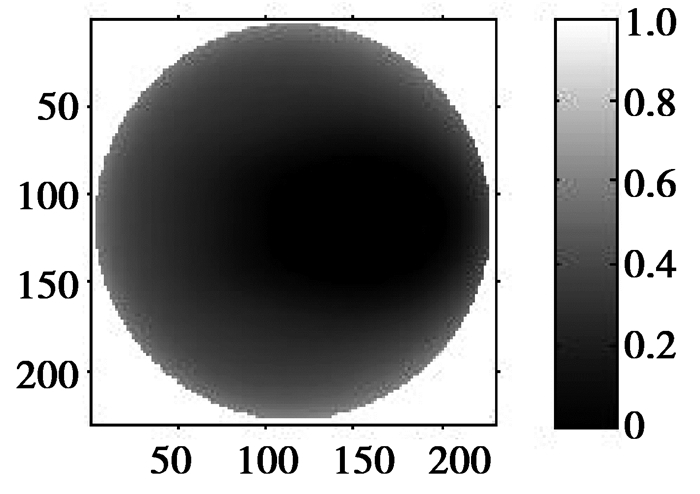
由于每一组检测器只有8个检测线圈,数据量不足,在程序中用线性插值补充数据的不足,用Hamming滤波器对数据进行滤波,滤波器可以补偿投影中的高频成分和降低投影中心密度。运用图 4的归一化数据重构了像素230×230的图像,成像结果如图 5所示。
|
图 5 滤波反投影成像结果 |
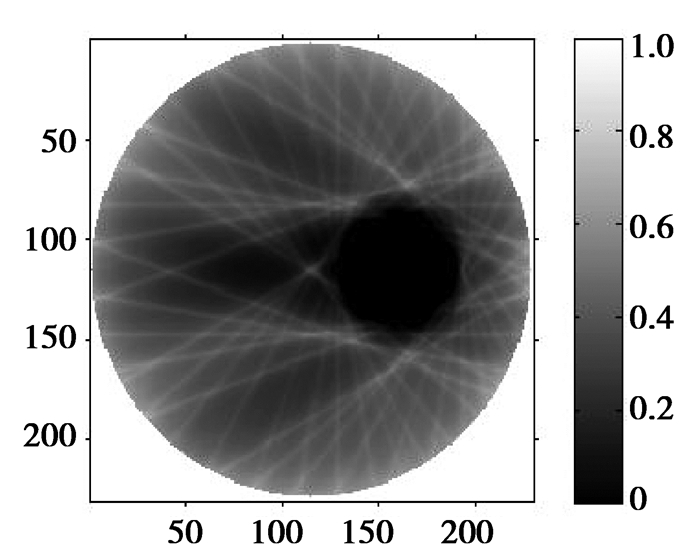
在MIT测量系统中,由于涡流产生的磁场是发散的,使得图形边缘模糊,物体扩大,加入窗口滤波器减少涡流磁场发散对周围检测线圈的影响,使物体轮廓更清晰,其成像结果如图 6所示。比较图 5和图 6,可以明显看出图 6结果与实际模型相差较小。
|
图 6 加入窗口滤波器滤波反投影成像结果 |
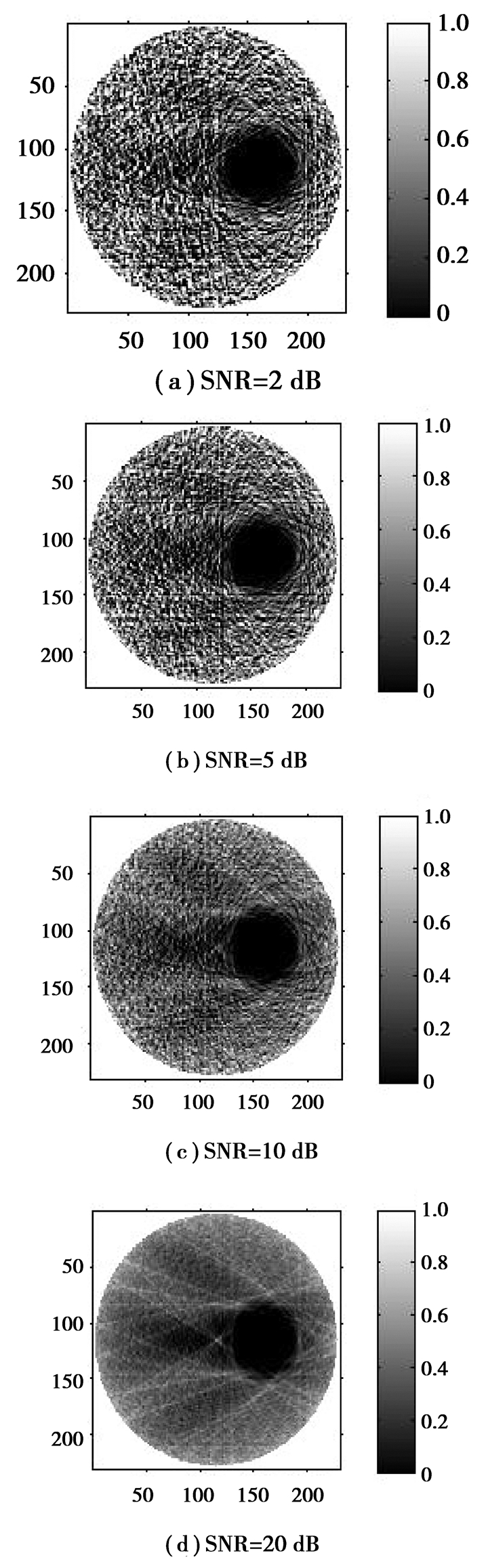
前面的研究是没有测量噪声干扰下得出的结论。但是实际MIT成像系统中含有各种噪声因素,该算法是否仍然能对目标进行准确定位,值得进一步研究。分别在检测电压中加入SNR为2,5,10,20 dB后,利用该算法对仿真模型进行图像重建得到图像如图 7所示。将图 7中(a)、(b)、(c)、(d)与不含噪声的情况比较,可以看出该算法具有很好的抗噪声能力。
|
图 7 不同信噪比的成像结果 |
文中通过分析比较传统MIT系统的激励系统,提出用亥姆霍兹线圈建立激励磁场,此方法产生了较均匀且方向一致的磁场,显著减少了图像重构的复杂度和计算量。结合MIT实际情况改进了滤波反投影重构算法。通过对8通道的测量系统建模仿真,系统旋转一周测量了36组数据,验证了使用滤波反投影在MIT系统中电导率重构中的可行性;对仿真数据进行噪声干扰,可以看出滤波反投影重构算法有很好的抗噪性能。以上研究和分析表明,利用加入窗口滤波器的滤波反投影重构算法可以更好地显示出目标物体,但是如果成像区域复杂,用这种简单的窗口滤波器比较困难。在后面的研究工作中还要进一步改进窗口滤波器,从而推进MIT技术向医学实时监护应用。
| [1] | 何为, 罗辞勇, 徐征. 电阻抗成像原理[M]. 北京: 科学出版社, 2009. |
| [2] | 刘国强. 医学电磁成像[M]. 北京: 科学出版社, 2006. |
| [3] | Xu Z, Luo H J, He W, et al. A multi-channel magnetic induction tomography measurement system for human brain model imaging[J]. Physiological Measurement, 2009, 30(6): 175–186. DOI:10.1088/0967-3334/30/6/S12 |
| [4] |
徐征, 何为, 何传红, 等.
生物组织电导率磁感应测量原理及系统研究[J]. 仪器仪表学报, 2008, 29(9): 1878–1882.
XU Zheng, HE Wei, HE Chuanhong, et al. Study on the principles and system of measurement biological tissue conductivity with magnetic induction method[J]. Chinese Journal of Scientific Instrument, 2008, 29(9): 1878–1882. (in Chinese) |
| [5] | Korjenevsky A, Cherepenin V, Sapetsky S. Magnetic induction tomography:experimental realization[J]. Physiological Measurement, 2000, 21(1): 89–94. DOI:10.1088/0967-3334/21/1/311 |
| [6] | Watson S, Williams R J, Gough W, et al. A magnetic induction tomography system for samples with conductivities below 10 S/m[J]. Measurement Science and Technology, 2008, 19(4): 1–11. |
| [7] | Gürsoy D, Scharfetter H. The effect of receiver coil orientations on the imaging performance of magnetic induction tomography[J]. Measurement Science and Technology, 2009, 20(10): 1–9. |
| [8] | Gürsoy D, Scharfetter H. Reconstruction artefacts in magnetic induction tomography due to patient's movement during data acquisition[J]. Physiological Measurement, 2009, 30(6): 165–174. DOI:10.1088/0967-3334/30/6/S11 |
| [9] | Merwa R, Hollaus K, Brunner P, et al. Solution of the inverse problem of magnetic induction tomography (MIT)[J]. Physiological Measurement, 2005, 26: 241–250. DOI:10.1088/0967-3334/26/2/023 |
| [10] | Merwa R, Brunner P, Missner A, et al. Solution of the inverse problem of magnetic induction tomography (MIT) with multiple objects:analysis of detectability and statistical properties with respect to the reconstructed conducting region[J]. Physiological Measurement, 2006, 27(5): 249–259. DOI:10.1088/0967-3334/27/5/S21 |
| [11] | Vauhkonen M, Hamsch M, Iqney C H. A measurement system and image reconstruction in magnetic induction tomography[J]. Physiological Measurement, 2008, 29(6): 445–454. DOI:10.1088/0967-3334/29/6/S37 |
| [12] |
王聪, 刘锐岗, 李烨, 等.
一种用于磁感应断层成像的图像重建算法[J]. 仪器仪表学报, 2008, 29(10): 2052–2057.
WANG Cong, LIU Ruigang, LI Ye, et al. Image reconstruction algorithm for magnetic induction tomography[J]. Chinese Journal of Scientific Instrument, 2008, 29(10): 2052–2057. DOI:10.3321/j.issn:0254-3087.2008.10.007 (in Chinese) |
| [13] | 柯丽, 杜强, 王旭. 基于滤波反投影的磁感应图像重建算法研究[C]. 第七届全国信息获取与处理学术会议论文集, 广西, 2009: 5-7. |
| [14] |
陈玉艳, 王旭, 吕轶, 等.
基于Tikhonov和变差正则化的磁感应断层成像重建算法[J]. 东北大学学报:自然科学版, 2011, 32(4): 460–463.
CHEN Yuyan, WANG Xu, Lü Yi, et al. An image reconstruction algorithm based on Tikhonov and variation regularization for magnetic induction tomography[J]. Journal of Northeastern University:Natural Science Ediction, 2011, 32(4): 460–463. (in Chinese) |
| [15] |
黄嵩, 何为, 罗辞勇.
开放式电阻抗成像中变差正则化重构算法[J]. 重庆大学学报, 2011, 34(10): 1–7.
HUANG Song, HE Wei, LUO Ciyong. Open-electrical impedance tomography with variation regularization algorithm[J]. Journal of Chongqing University, 2011, 34(10): 1–7. (in Chinese) |
| [16] | 雷银照. 轴对称线圈磁场计算[M]. 北京: 中国计量出版社, 1991. |
| [17] |
罗辞勇, 朱清友.
改进的电阻抗反投影成像算法[J]. 重庆大学学报, 2009, 32(3): 243–246.
LUO Ciyong, ZHU Qinyou. An improved back-projection algorithm for electrical impedance tomography[J]. Journal of Chongqing University, 2009, 32(3): 243–246. DOI:10.11835/j.issn.1000-582X.2009.03.001 (in Chinese) |
 2013, Vol. 36
2013, Vol. 36


