2. 合肥供电局, 合肥 230000
2. Electric Power Supply Bureau of Hefei, Hefei 230000, China
随着我国经济的快速发展,电力需求急剧增加。我国能源分布与电力负荷不平衡,决定了我国长距离的“西电东送”政策。对于这种大容量,长距离的电力输送,特高压直流输电较传统的交流输电更具优势,有着广阔的应用前景。特高压直流线路电晕是其在输电过程中产生能量损耗的主要因素,对特高压直流线路电晕进行分析有着重要的价值和现实的实际意义。但是双极分裂导线起晕过程的复杂性增加了分析高压线路电晕损耗的复杂程度。
人们很早就开始对电晕现象进行了研究,像比较著名的皮克公式[1]被广泛用来预测导线起晕电压和电场。但皮克公式是一个经验公式,它并不能反映电晕的全部物理过程,它也没有考虑到导线对地高度影响。早在20世纪60年代Sarma等人就对单极和双极的单导线进行了一系列研究[2-3]。随后出现各种数值算法,文献[4]用有限元法分析了双极单导线电晕条件下的离子流场,文献[5]用模拟电荷法分析计算了双极分裂导线的电晕损耗,文献[6-7]分别采用模拟电荷有限元结合法和边界元法。以上文献都做了一些假设,其中都认为导线表面的起晕电压不变,并将其作为求解离子流场的边界条件,而实际上由于各个子导线相互影响,子导线表面周围的起晕电压不是一个恒定值,这必然导致计算结果的不准确。
分裂导线的处理上,有些力求找到合适的单根等效单导线半径。等效原则为等效导线的表面标称场强与分裂导线表面的标称场强的平均值相等,并且等效导线与原分裂导线的起晕场强相同[8]。这种方法适合分析导线外部的场,但等效以后不能计算各个子导线的电晕情况。
笔者考虑到子导线相互作用(文献[9]认为子导线所分布的圆的内侧起始电场线相互抵消忽略不计),对子导线单独考虑,每个子导线用一组模拟电荷精确模拟,准确计算子导线表面电场,根据电晕理论得出起晕电压和起晕场强。在此基础上,提出了分析双极分裂导线离子流的方法,进而计算出电晕电流,得出电晕损耗。最后分析±800 kV线路地面标称与合成电场验证方法的正确性。
1 计算方法 1.1 起晕电压的计算笔者不考虑正负极电晕的差异。根据电晕放电产生的机理[10],可知初始电子崩头部的电子数达到一定数目时,初始电子崩转化为流注放电,从而形成电晕自持放电。初始电子崩头部的电子数由式(1)决定:
| $ n = {n_0}\exp \left( {\int_0^d {\left( {\alpha - \eta } \right){\rm{d}}x} } \right), $ | (1) |
其中:n为经过d后电子崩头部自由电子数;n0为空间存在的初始自由电子数;α为Townsend第一电离系数;η为电子附着系数;d为电子崩的临界长度(即电晕层厚度),也就是从导体表面到α=η的长度。在空气中,α和η是电场强度和大气压的函数。由于初始电子数n0不易确定,因此用
考虑空间电荷的存在,根据电磁场基本理论可以得到描述双极离子流场的数学方程:
| $ \left\{ \begin{array}{l} \nabla \cdot \mathit{\boldsymbol{E}} = \frac{{{\rho _ + } - {\rho _ - }}}{{{\varepsilon _0}}},\\ {\mathit{\boldsymbol{J}}_ + } = {k_ + }{\rho _ + }\mathit{\boldsymbol{E}},\\ {\mathit{\boldsymbol{J}}_ - } = {k_ - }{\rho _ - }\mathit{\boldsymbol{E}},\\ \nabla \cdot {\mathit{\boldsymbol{J}}_ + } = - \frac{{{R_i}{\rho _ + }{\rho _ - }}}{e},\\ \nabla \cdot {\mathit{\boldsymbol{J}}_ - } = \frac{{{R_i}{\rho _ + }{\rho _ - }}}{e},\\ \mathit{\boldsymbol{E}} = - \nabla \mathit{\Phi }; \end{array} \right. $ | (2) |
式中:E和Φ分别为合成场、合成电位;J+和J-分别为正负离子流密度;ρ+和ρ-分别为正负电荷密度;k+和k-分别为正负离子迁移率;Ri为正负离子复合系数;e为一个电子的电量;ε0为真空中的介电常数。
1.2.2 基本假设和计算的数学方程严格推导出来的直流输电线路合成场和离子流密度的方程非常复杂,从工程应用考虑,笔者采用的假设有:
1) Deutecsh假设,即空间电荷只影响电场的幅值而不改变其方向。
2) 离子的迁移率是与电场无关的常数且认为正负离子的迁移率相等。
3) 不考虑离子的扩散,带电离子只受电场力的作用沿着电场线方向运动。
4) 忽略导线表面电晕层的厚度。
5) 不考虑正负极的差异,正负极的起晕电压相同。
根据假设1)有
| $ \mathit{\boldsymbol{E}} = A{\mathit{\boldsymbol{E}}_s}, $ | (3) |
其中Es、E分别为标称电场、合成电场;A为关于空间位置的标量函数。
由式(2)、(3)可以推出
| $ \left\{ \begin{array}{l} \frac{{{\rm{d}}\mathit{\Phi } }}{{{\rm{d}}{\mathit{\Phi } _s}}} = A,\\ \frac{{{\rm{d}}A}}{{{\rm{d}}{\mathit{\Phi } _s}}} = - \frac{{{\rho _ + } - {\rho _ - }}}{{{\varepsilon _0}{{\left( {{E_s}} \right)}^2}}},\\ \frac{{{\rm{d}}{\rho _ + }}}{{{\rm{d}}{\mathit{\Phi } _s}}} = \frac{1}{{{\varepsilon _0}A{{\left( {{E_s}} \right)}^2}}}\left( {\rho _ + ^2 - {\rho _ + }{\rho _ - } + \frac{{{\varepsilon _0}{R_i}{\rho _ + }{\rho _ - }}}{{ke}}} \right),\\ \frac{{{\rm{d}}{\rho _1}}}{{{\rm{d}}{\mathit{\Phi } _s}}} = \frac{1}{{{\varepsilon _0}A{{\left( {{E_s}} \right)}^2}}}\left( { - \rho _ - ^2 + {\rho _ + }{\rho _ - } - \frac{{{\varepsilon _0}{R_i}{\rho _ + }{\rho _ - }}}{{ke}}} \right)。\end{array} \right. $ | (4) |
Φs为标称电位。
其边界条件为
1) 在地面和正负极的中轴线上,Φ=0, Φs=0。
2) 在子导线表面Φ=V,Φs=V,其中V是导线的运行电压。
3) 在导线表面Ae=V0(αk)/V, V0(αk)是子导线表面的起晕电压,其中αk为子导线表面的点相对于其圆心的角度,如图 1所示。

|
图 1 ±800 kV线路布置及模拟电荷的配置 |
在已知标称量的情况下,根据边界条件,微分方程(4)是可解的。沿电场线从子导线表面出发,给定一个初始电荷密度ρe,迭代求解微分方程就能确定该条电场线上各点的合成电场和电荷密度。改变ρe直至满足边界条件,此时的ρe即为真实值。在求解微分方程时采用四阶龙格库塔法。
子导线的电晕电流为
| $ {I_c} = rk\int\limits_0^{2{\rm{ \mathsf{ π} }}} {{\rho _e}{A_e}{E_{se}}{\rm{d}}{\alpha _k}} 。$ | (5) |
相应的功率损耗为
| $ P = V{I_c}, $ | (6) |
式中:Ese为子导线表面的标称电场大小;V为导线运行电压。
在上述过程中,用模拟电荷法计算标称场。
2 算例分析向家坝—上海±800 kV直流输电工程,如图 1的布置,实心点代表模拟电荷,空心点代表匹配点,rs是模拟电荷到子导线中心的距离。线路选用6×720 mm2导线。子导线的起始角为0度,极间距D=22 m,导线对地高度H一般地区最小取18 m,临近居民区时最小取21 m。分裂半径R=0.45 m,子导线半径r0=17.2 mm。根据DL/T436-2005《高压直流架空送电线路技术导则》,粗糙系数m取0.47。计算时,认为正负极对称,只考虑第一象限,以X,Y正半轴为边界,正极性导线初始电荷密度
图 2给出了H=21 m时计算的地面标称场和合成场的结果。表 1给出了H=18 m时与文献[12]的比较结果。

|
图 2 地面合成场与标称场(H=21 m) |
| 表 1 本文计算结果与文献[12]比较 |
H=18 m时,根据式(1)计算的起晕电压和起晕电场如图 3所示。

|
图 3 子导线表面起晕电压和起晕电场的分布(H=18 m) |
图 3起晕电场和DL/T436-2005《高压直流架空送电线路技术导则》规定18 kV/cm非常接近。从表 1和图 2,3可以看出,地面标称电场、合成电场最大值以及起晕电场都与已出版的文献吻合得很好,可以说明本文方法是准确有效的。另外图 3还可以看出各子导线表面的起晕电压变化很大。子导线所在圆的内侧,起晕电压超过了800 kV没有发生电晕。不考虑离子的扩散,从这里出发的电场线上没有空间电荷,合成场等于标称场,这解释了图 2给出的合成电场在距离线路中心20~30 m之间有一部分比较接近标称电场的原因。
图 4给出了H=18 m时,正极各分裂子导线表面一周电晕电流的分布。图 5给出了各子导线的电晕损耗。由式(5)、(6)计算得出双极电晕损耗P=5.054 W/m。向家坝-上海直流输电工程线路长1 900 km,输送容量6 400 MW。按此损耗计算,电晕损耗占输送容量的0.15%。

|
图 4 子导线表面一周电晕电流分布(H=18 m) |

|
图 5 各子导线电晕损耗(H=18 m) |
从图 5可以看出各子导线的损耗并不相同,损耗主要集中在子导线3、4、5,占正极总损耗的83.1%,这是由于负极导线增强了子导线3、4、5表面的电场,使其电晕程度严重。
3 线路参数对电晕的影响分析±800 kV,6×720 mm2输电线路,H=18 m,D=22 m,R=0.45m,r0=17.2 mm,为了更好地分析某一参数的影响,当其中一个参数改变时,其他参数保持不变。
3.1 子导线半径的影响±800 kV高压直流输电线路,极间距D=22 m,分裂半径R=45 cm,导线对地高度H=18 m,改变子导线半径,计算得到的各子导线电晕损耗如图 6所示。从图中可以看出,随着子导线半径的增大,r0从15 mm到17.2 mm,17.2 mm到18.3 mm,从18.3 mm到20.3 mm各子导线总的电晕损耗分别减少了2.04,0.64,0.83 W/m,电晕损耗减少得很快。这是因为子导线半径对其表面电场影响很大,随着子导线半径增大,其表面电场迅速减小,从而减轻电晕的严重程度。

|
图 6 子导线半径对电晕损耗的影响 |
±800 kV高压直流输电线路,分裂半径R=45 cm,极间距D=22 m,子导线半径r0=17.2 mm,改变导线对地高度,计算得到结果如图 7所示。从图中可以看出随着高度的增大,电晕损耗逐渐减小。对地高度H从15 m到18 m,18 m到21 m,21 m到25 m,各子导线总的电晕损耗分别减少了0.56,0.19,0.19 W/m,减少得不明显,这是因为高度影响镜像电荷的距离,镜像电荷与实际的电荷电性相反,他们相互作用会加强彼此导线附近的电场。但是由于导线对地高度分别取15,18,21,25 m,实际上镜像电荷和实际电荷的距离都超过了30 m,由于距离较远,这种影响变得很弱,因此对电晕损耗的影响不明显。

|
图 7 导线对地高度对电晕损耗的影响 |
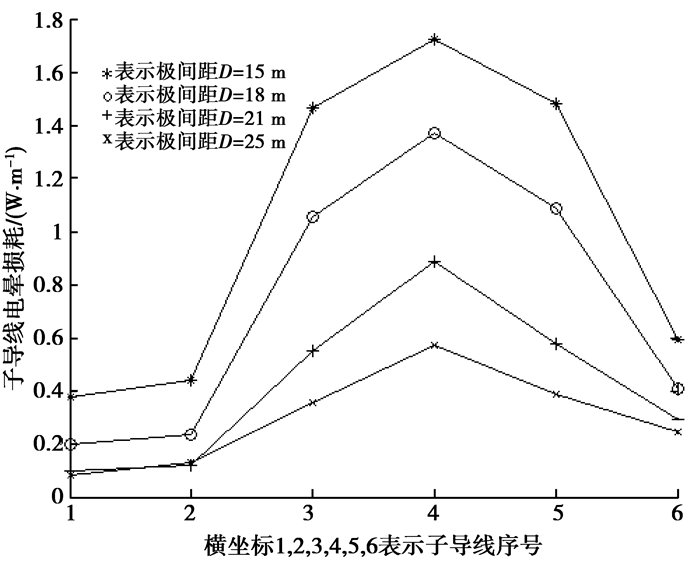
±800 kV高压直流输电线路,分裂半径R=45 cm,导线对地高度H=18 m,子导线半径r0=17.2 mm,改变极间距,计算得到结果如图 8所示。从图上可以看出随着极间距的增大,电晕损耗减小很快,影响比较显著。分裂间距D从15 m到18 m,18 m到22 m,22 m到25 m各子导线总电晕损耗分别减少了1.72,1.83,0.76 W/m。实际上这里的原因和对地高度的作用机理是一样的,正负极的作用使彼此附近的电场加强,这是由于这里极间距小了,正负极相互作用比较明显。
|
图 8 极间距对电晕损耗的影响 |
±800 kV高压直流输电线路,极间距D=22 m,导线对地高度H=18 m,子导线半径r0=17.2 mm,改变分裂半径,计算得到结果如图 9所示。随着分裂半径的增大电晕损耗在增加。分裂半径R从20 cm到30 cm,30 cm到45 cm,45 cm到60 cm各子导线总的电晕损耗分别增加了0.05,0.47,1.05 W/m。可以看到当R < 30 cm时对电晕损耗几乎没有影响。分裂导线极性相同,他们相互减弱各自附近的电场,R < 30 cm时这种作用已经很强烈,再减小R对电晕损耗的影响就不再明显;当R > 30 cm时,这种作用减弱比较显著,子导线表面电场变大,电晕损耗增加相对明显。

|
图 9 分裂半径对电晕损耗的影响 |
由图 6~9可以知道:随着子导线半径的增大,导线高度的升高,极间距的增大,电晕损耗减小;随着分裂半径的增加,电晕损耗增大。但是它们影响的程度不一样。子导线半径和极间距对电晕损耗比较明显,是主要因素;导线高度的影响较小;当分裂半径大于0.45 m时,随着分裂半径的增大电晕损耗增加较快,当分裂半径小于0.30 m时,对电晕损耗的影响不明显。
4 结论1) 笔者从理论上分析,根据双极直流线路离子流的数学方程,推导出计算电晕的数学模型。相对电晕的经验公式,能考虑电晕的物理过程以及线路各种参数对电晕损耗的影响,并能够分析其具体原因。
2) 考虑了分裂导线表面电晕程度不同这一实际情况,子导线表面从其所分布的圆的外侧到内侧电晕损耗逐渐减轻,在内侧甚至可能不起晕,计算时对这一情况区别对待,使计算结果相对更加准确。
3) 由于每个子导线的位置不同,各个子导线的电晕损耗也不相同。800 kV六分裂线路每一极的电晕损耗主要集中在线路内侧的3个子导线上,占总损耗的80%以上。
4) 分析了输电线高度、极间距、子导线半径、分裂半径对电晕损耗的影响。结果表明随着子导线半径的增大,导线高度的升高,极间距的增大,电晕损耗减小;随着分裂半径的增加,电晕损耗增大。进一步分析,子导线半径和极间距是影响电晕损耗的主要因素,因为这两个因素能比较明显地影响子导线表面电场从而影响电晕损耗,工程设计时应该优先考虑。另外分裂间距较大时也会对电晕损耗产生较大影响。
| [1] | Peek F W. Dieletric phenomena in high voltage engineering[M]. New York: McGraw-Hill, 1929. |
| [2] | Sarma M P, Janischewskyj W. Analysis of corona losses on DC transmission lines part Il bipolar lines[J]. IEEE Transactions on Power Apparatus and Systems, 1969, 88(10): 1476–1491. |
| [3] | Sarma M P, Janischewskyj W. Analysis of corona losses on DC transmission lines:1-unipolar lines[J]. IEEE Transactions on Power Apparatus and Systems, 1969, 88(5): 718–731. |
| [4] | Abdel-Salam M, Al-Hamouz Z. A finite-element analysis of bipolar ionized field[J]. IEEE Transactions on Industry Applications, 1995, 31(3): 477–483. DOI:10.1109/28.382106 |
| [5] | Al-Hamouz Z M. Corona power loss, electric field, and current density profiles in bundled horizontal and vertical bipolar conductors[J]. IEEE Transactions on Industry Applications, 2002, 38(5): 1182–1189. DOI:10.1109/TIA.2002.802931 |
| [6] | Al-Hamouz Z M. A hybrid computational technique for the estimation of corona power loss associated with bundled transmission lines[J]. Electric Power Systems Research, 1999, 50(1): 65–70. DOI:10.1016/S0378-7796(98)00154-0 |
| [7] | Yu M, Kuffel E, Poltz J. A new algorithm for calculating HVDC corona with the presence of wind[J]. IEEE Transactions on Magnetics, 1992, 28(5): 2802–2804. DOI:10.1109/20.179632 |
| [8] | Sunaga Y, Sawada Y. Method of calculating ionized field of HVDC transmission lines and analysis of space charge effects on RI[J]. IEEE Transactions on Power Apparatus and Systems, 1980, 99(2): 605–615. |
| [9] |
袁海燕, 傅正财.
基于有限元法的±800kV特高压直流输电线路离子流场计算[J]. 电工技术学报, 2010, 25(2): 139–146.
YUAN Haiyan, FU Zhengcai. Corona ionized field analysis of ±800kV HVDC transmission lines[J]. Transactions of China Electrotechnical Society, 2010, 25(2): 139–146. (in Chinese) |
| [10] | 徐学基, 诸定昌. 气体放电物理[M]. 上海: 复旦大学出版社, 1996. |
| [11] | Yamazaki K, Olsen R G. Application of a corona onset criterion to calculation of corona onset voltage of stranded conductors[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2004, 11(4): 674–680. DOI:10.1109/TDEI.2004.1324356 |
| [12] | 刘振亚. 特高压电直流输电工程电磁环境[M]. 北京: 中国电力出版社, 2009. |
| [13] | Zangeneh A, Gholami A, Zamani V. A new method for calculation of corona Inception voltage in stranded conductors of overhead transmission lines[C]//Proceedings of the IEEE International Power and Energy Coference, November 28-29, 2006, Putrajaya, Malaysia. Piscataway:IEEE Press, 2006:571-575. |
| [14] | Li Z X, Li G F, Fan J B, et al. Numerical calculations of monopolar corona from the bare bundle conductors of HVDC transmission lines[J]. IEEE Transactions on Power Delivery, 2009, 24(3): 1579–1585. DOI:10.1109/TPWRD.2009.2014273 |
| [15] | Phillips D B, Olsen R G, Pedrow P D. Corona onset as a design optimization criterion for high voltage hardware[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2000, 7(6): 744–751. DOI:10.1109/94.891984 |
 2013, Vol. 36
2013, Vol. 36

