2. 日本千叶大学 机械工程系, 千叶 263-8522
2. Department of Mechanical Engineering, Chiba University, Chiba 263-8522, Japan
两相流动问题广泛存在于能源与动力、化工、核反应堆等工程设备与生产工艺当中。两相流的数值模拟方法的研究长期以来倍受人们的关注。
目前,模拟两相流的数值方法主要有拉格朗日法[1]、混合拉格朗日欧拉法[2]和欧拉法[3]等。在拉格朗日法中,网格随界面运动而发生变形和扭曲,有时会导致网格因变形过大而畸变。尽管针对拉格朗日法引入了一些新算法,一定程度上解决了网格畸变等问题,但不能像欧拉法那样自然的反映大变形情况。混合拉格朗日欧拉法主要有CEL(coupled eulerian Lagrangian)法和任意拉格朗日欧拉法(arbitrary Lagrangian eulerian method/ALE)[2]法。在利用ALE法模拟两相流过程中,需要进行网格重分,以保证相界面与网格边界对齐。采用固定网格的欧拉法是目前两相流数值模拟最为通用的方法。基于界面标记点的PIC(particle in cell)方法和MAC(marker in cell)方法是一类早期的固定网格方法。Hirt等将标记点改进为标记函数,提出了VOF(volume of fluid)方法[3]。该方法通过计算含标记函数的输运方程达到追踪界面的目的,但需要进行较复杂的界面重构。水平集(level set)方法是Osher等提出的一种运动界面捕捉技术[4],该方法通过定义符号距离函数,相界面可以由距离函数的零等值线确定。水平集方法在两相流有限元方法中已经得到应用[5]。
在以上各种模拟两相流的常规方法中,通常需要相界面两侧的网格对齐,或者在相界面增大网格密度,进行网格重构等。Belytschko等提出的扩展有限元方法(XFEM)[6],是为避免网格重构而提出的一个解决方法,该方法最初用来解决裂纹尖端不连续场问题。扩展有限元的网格生成不需要考虑界面的存在,其基于单位分解法[7],在单元形函数中增加与界面相关的附加形函数,改善有限元逼近空间。在常规扩展有限元方法(standard XFEM)中,混合区的混合单元并不能满足单位分解的要求。为此,出现了解决这一问题的几种方法[8-10]。
Chessa等最早将扩展有限元方法用于两相流数值模拟中[11],他们用基于特征分裂法离散控制方程,被相界面贯穿的单元通过引入附加函数来描述不连续性,并对气泡上升问题进行了数值模拟研究,得到与实验规律一致的结果。但其未对混合区的混合单元进行有效处理,混合单元不满足单位分解原理。Fries则采用一种与无网格方法类似,基于移动最小二乘法(MLS)的本质扩展有限元方法(intrinsic XFEM)[12],模拟分析了气泡在不同Morton数下的运动状态。该方法不需要引入附加节点未知量,但在加强区节点权函数计算过程中,与无网格法类似,需要遍历影响区内的每个节点,计算规模较大。
笔者采用SUPG/PSPG[13-14]有限元格式离散流体动力学控制方程,界面贯穿单元的形函数通过引入附加函数来改善逼近空间,并首次采用修正/加权扩展有限元方法(corrected/weighted XFEM)使混合单元满足单位分解原理。两相流的相界面采用水平集函数描述,捕捉两相界面的运动。通过液箱晃荡及溃坝问题的数值模拟, 验证了方法的正确性和有效性。
1 两相流控制方程两相流体求解域如图 1所示。
|
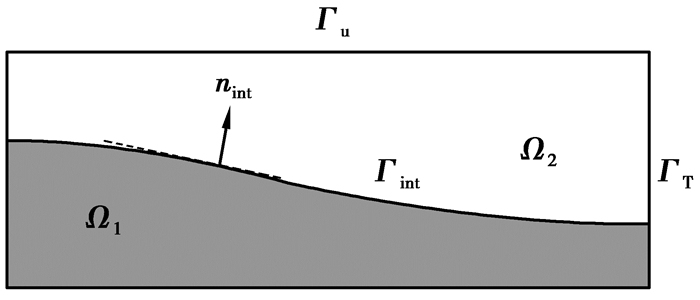
图 1 两相流体流动的求解域 |
图 1区域中包含2种互不相融合的不可压缩流体Ω1和Ω2。在两相流体流动过程中,相界面Γint随时间变化。边界包含Dirichlet边界Γu和Neumann边界ΓT。流体动力学控制方程为
| $ \begin{array}{*{20}{c}} {\rho \left( {\frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial t}} + \mathit{\boldsymbol{u}} \cdot \nabla \mathit{\boldsymbol{u}} - \mathit{\boldsymbol{f}}} \right) - \nabla \cdot \mathit{\boldsymbol{\sigma }} = 0,}\\ {\nabla \cdot \mathit{\boldsymbol{u}} = 0,} \end{array} $ | (1) |
式中:ρ为流体密度;u为速度场;f为附加重力项;σ为柯西应力,可分解为偏斜应力τ和静水压力p。
| $ \mathit{\boldsymbol{\sigma }} = \mathit{\boldsymbol{\tau }} - p\mathit{\boldsymbol{I}}。$ | (2) |
对于牛顿流体
| $ \mathit{\boldsymbol{\tau }} = 2\mu \mathit{\boldsymbol{D}},\mathit{\boldsymbol{D}} = \frac{1}{2}\left( {\nabla \mathit{\boldsymbol{u}} + {{\left( {\nabla \mathit{\boldsymbol{u}}} \right)}^{\rm{T}}}} \right)。$ | (3) |
式中,μ为粘性系数。
Dirichlet和Neumann边界条件分别为:
| $ \mathit{\boldsymbol{u}}\left( {\mathit{\boldsymbol{x}},t} \right) = \mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over u} }}\forall \mathit{\boldsymbol{x}} \in {\mathit{\Gamma }_{\rm{u}}}, $ | (4) |
| $ \mathit{\boldsymbol{n}} \cdot \mathit{\boldsymbol{\sigma }}\left( {\mathit{\boldsymbol{x}},t} \right) = \mathit{\boldsymbol{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}} \over u} }}\forall \mathit{\boldsymbol{x}} \in {\mathit{\Gamma }_{\rm{t}}}。$ | (5) |
在忽略表面张力的情况下,应力场和速度场在相界面需满足以下条件
| $ \left[ {{\mathit{\boldsymbol{n}}_{{\mathop{\rm int}} }} \cdot \mathit{\boldsymbol{\sigma }}} \right] = 0, $ | (6) |
| $ \left[ \mathit{\boldsymbol{u}} \right] = 0, $ | (7) |
式中,nint为相界面的法向矢量。
对于两相流体,ρ和μ定义如下:
| $ \rho \left( \varphi \right) = \left\{ \begin{array}{l} {\rho _1}\;\;\;\;\;\varphi \ge 0\\ {\rho _2}\;\;\;\;\;\varphi < 0 \end{array} \right.\;\;\;\;\;\forall \mathit{\boldsymbol{x}} \in \mathit{\Omega }, $ | (8) |
| $ \mu \left( \varphi \right) = \left\{ \begin{array}{l} {\mu _1}\;\;\;\;\;\varphi \ge 0\\ {\mu _2}\;\;\;\;\;\varphi < 0 \end{array} \right.\;\;\;\;\;\forall \mathit{\boldsymbol{x}} \in \mathit{\Omega }。$ | (9) |
式中,φ为水平集函数,该函数用于跟踪描述两相流体的界面,这里
| $ \varphi \left( {\mathit{\boldsymbol{x}},t} \right)\left\{ \begin{array}{l} < 0\;\;\;\;\forall \mathit{\boldsymbol{x}} \in {\mathit{\Omega }_1}\\ = 0\;\;\;\;\forall \mathit{\boldsymbol{x}} \in {\mathit{\Gamma }_{{\mathop{\rm int}} }}\\ < 0\;\;\;\;\forall \mathit{\boldsymbol{x}} \in {\mathit{\Omega }_2} \end{array} \right.。$ | (10) |
考察两相流求解区域,Ω⊂R2被分割成一系列的子单元Ωe,I为单元节点集合。假设插值形函数为Ni(x),常规扩展有限元速度场插值形式可描述为:
| $ {u^h}\left( {x,t} \right) = \sum\limits_{i \in I} {{N_i}\left( x \right){u_i}} + \sum\limits_{i \in {I^ * }} {{M_i}\left( {\mathit{\boldsymbol{x}},t} \right){a_i}} 。$ | (11) |
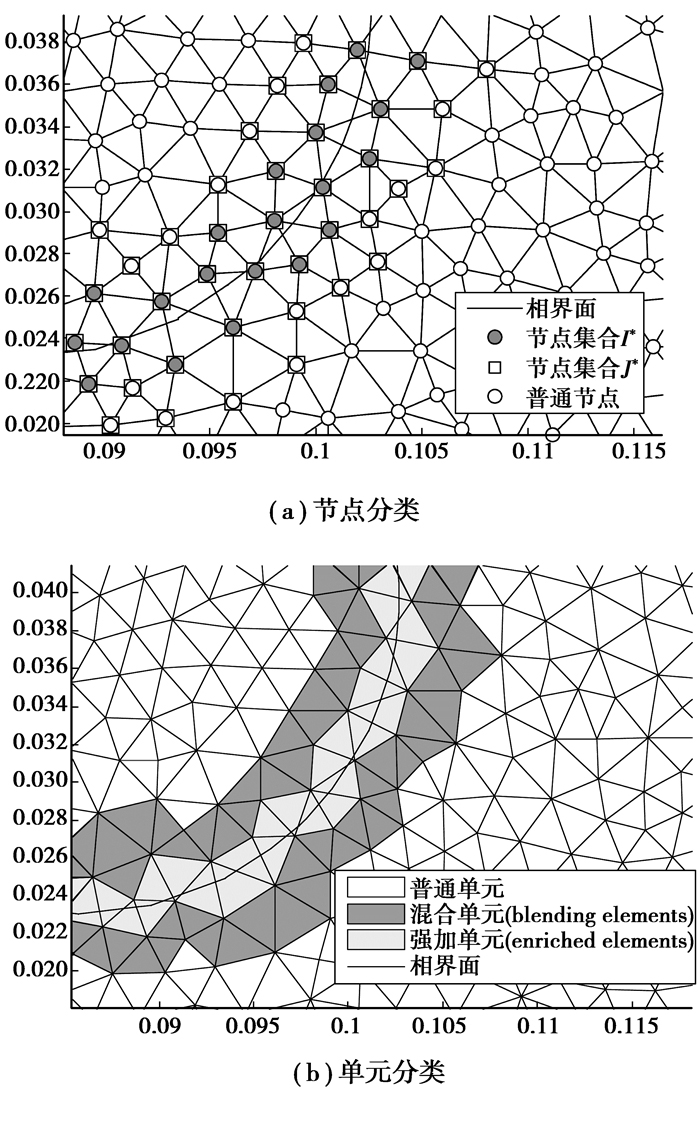
由于相界面的存在而需要增加自由度的单元节点集合,称之为I*,I*⊂I,如图 2(a)所示。其中ui为有限元节点未知量,ai为由于附加节点而产生的附加变量,Mi(x, t)为附加形函数。按照以下方式定义:
| $ {M_i}\left( {x,t} \right) = {N_i}\left( x \right){\mathit{\Psi }_J}\left( {\mathit{\boldsymbol{x}},t} \right), $ | (12) |
| $ {\mathit{\Psi }_J}\left( {x,t} \right) = \left| {\varphi \left( {x,t} \right)} \right| - \left| {\varphi \left( {{\mathit{\boldsymbol{x}}_J},t} \right)} \right|。$ | (13) |
被附加形函数加强的单元分两类,参见图 2(b)。一类是界面贯穿单元,这类单元全部节点都被附加形函数加强,将这些单元称为全加强单元。由于附加函数基于单位分解法,故全加强单元满足
|
图 2 扩展有限元模型中节点和单元分类 |
为改进扩展有限元附加形函数在混合单元内不满足单位分解性质的缺点,采用Fries提出的一种修正方法[15],定义如下改进的附加形函数
| $ M_i^ * \left( {\mathit{\boldsymbol{x}},t} \right) = {N_i}\left( x \right){\mathit{\Psi }_J}\left( {x,t} \right) \cdot R\left( x \right), $ | (14) |
式中,R(x)为平滑函数,定义为:
| $ R\left( \mathit{\boldsymbol{x}} \right) = \sum\limits_{i \in {I^ * }} {{N_i}\left( \mathit{\boldsymbol{x}} \right)} 。$ | (15) |
在贯穿单元中的R(x)函数,由于其节点全部处于I*集合中,故R(x)=1。在普通单元中不含加强节点,R(x)=0。在混合单元中,包含部分加强节点,因此R(x)的值在0~1之间。经修正后,贯穿单元与混合单元的附加形函数都满足单位分解原理。与常规扩展有限元相比,该方法在混合单元包含更多的附加形函数,因此需要更多的积分点保证积分精度。
改进的扩展有限元加强节点集合J*,如图 2(a)所示,J*⊂I。J*是所有加强单元和混合单元节点的集合。因此I*⊂J*。修正后的扩展有限元插值形式为
| $ \begin{array}{*{20}{c}} {{u^h}\left( {x,t} \right) = \sum\limits_{i \in I} {{N_i}\left( x \right){u_i}} + \sum\limits_{J \in {I^ * }} {{M_i}\left( {x,t} \right){a_i}} = }\\ {\sum\limits_{i \in I} {{N_i}\left( x \right){u_i}} + \sum\limits_{j = 1}^m {\sum\limits_{i \in {J^ * }} {{N_i}\left( x \right) \cdot \left( {\left| {{\varphi ^j}\left( {x,t} \right)} \right| - } \right.} } }\\ {\left. {\left| {{\varphi ^j}\left( {{x_i},t} \right)} \right|} \right) \cdot R\left( x \right) \cdot a_i^j。} \end{array} $ | (16) |
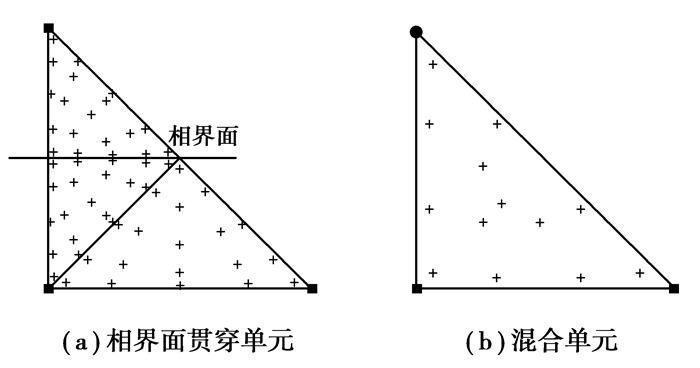
对于没有被相界面穿过的单元,采用标准的高斯积分方式。对于被相界面贯穿的单元,由于引入加强函数,形函数沿界面出现不连续现象。因此必须将单元分成子单元分别设置高斯点进行积分。子单元的划分依赖φ(x, t)函数在单元节点的值。可贯穿单元划分为3个子单元进行积分,如图 3所示。此外,根据文献[12],对混合单元选用比普通单元更多的积分点,以保证积分精确性。
|
图 3 相界面贯穿单元和混合单元积分点设置 |
水平集函数界面追踪法是一种隐式跟踪移动界面的技术,其基本思想是将随时间运动的物质界面定义为距离函数φ(x, t)的零等值面。水平集函数可用距离函数描述,其定义为:
| $ \varphi \left( {\mathit{\boldsymbol{x}},t} \right) = \pm \mathop {\min }\limits_{{x^ * } \in {\mathit{\Gamma }_{{\mathop{\rm int}} }}} \left\| {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}^ * }} \right\|\;\;\;\;\;\forall \mathit{\boldsymbol{x}} \in \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}。$ | (17) |
通过输运方程
| $ \frac{{\partial \varphi }}{{\partial t}} + \mathit{\boldsymbol{u}} \cdot \nabla \varphi = 0, $ | (18) |
即可追踪运动界面。为减少计算规模,文献[16]建议将上述方程改为:
| $ \frac{{\partial \varphi }}{{\partial t}} + c\left( \varphi \right)\mathit{\boldsymbol{u}} \cdot \nabla \varphi = 0。$ | (19) |
其中,截断函数
| $ c\left( \varphi \right) = \left\{ \begin{array}{l} 1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left| \varphi \right| \le \delta \\ \frac{{{{\left( {\left| \varphi \right| - \gamma } \right)}^2} \cdot \left( {2\left| \varphi \right| + \gamma - 3\delta } \right)}}{{\left( {\gamma - \delta } \right)}}\\ 0\;\;\;\;\;\;\;\;\;\left| \varphi \right| > \delta \end{array} \right.\;\;\;\;\;\;\delta < \left| \varphi \right| \le \gamma , $ | (20) |
式中:δ为截断距离,γ为平滑过渡距离。该函数的引入可以缩小水平集函数计算区域,进而大大减小计算规模。
笔者采用Sussman[17]提出的修正方法使φ保持为距离函数。距离保持方程如下:
| $ \frac{{\partial \varphi }}{{\partial t}} + {\rm{sign}}\left( {{\varphi ^n}} \right)\left( {\left| {\nabla \varphi } \right| - 1} \right) = 0。$ | (21) |
式中:sign()为符号函数,φn为tn时刻的解。
通过对输运方程(19)和距离保持方程(21)的有限元离散求解,即可达到捕捉运动界面的目的。定义的距离函数φ(x, t)将直接用于扩展有限元形函数的构造。
4 基于SUPG/PSPG的扩展有限元方程及其时间积分按照Tezduyar和Osawa提出的SUPG/PSPG稳定化方法[13],可写出流体动力学场方程的等效积分弱形式:
| $ \begin{array}{*{20}{c}} {\int\limits_\mathit{\Omega } {{\mathit{\boldsymbol{w}}^h} \cdot \rho \left( {\frac{{\partial {\mathit{\boldsymbol{u}}^h}}}{{\partial t}} + {\mathit{\boldsymbol{u}}^h} \cdot \nabla {\mathit{\boldsymbol{u}}^h} - \mathit{\boldsymbol{f}}} \right){\rm{d}}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}} + }\\ {\int\limits_\mathit{\Omega } {\mathit{\boldsymbol{\varepsilon }}\left( {{\mathit{\boldsymbol{w}}^h}} \right):\mathit{\boldsymbol{\sigma }}\left( {{p^h},{\mathit{\boldsymbol{u}}^h}} \right){\rm{d}}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}} - \int\limits_\mathit{\Gamma } {{\mathit{\boldsymbol{w}}^h} \cdot \mathit{\boldsymbol{h}}{\rm{d}}\mathit{\Gamma }} + \int\limits_\mathit{\Omega } {{q^h}\nabla \cdot {\mathit{\boldsymbol{u}}^h}{\rm{d}}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}} + }\\ {\sum\limits_{e = 1}^{{n_{e1}}} {\int\limits_{{\mathit{\Omega }^e}} {\frac{1}{\rho }\left[ {{\tau _{{\rm{SUPG}}}}\rho {\mathit{\boldsymbol{u}}^h} \cdot \nabla {\mathit{\boldsymbol{w}}^h} + {\tau _{{\rm{PSPG}}}}\nabla {q^h}} \right] \cdot } } }\\ {\left[ {\rho \left( {\frac{{\partial {\mathit{\boldsymbol{u}}^h}}}{{\partial t}} + {\mathit{\boldsymbol{u}}^h} \cdot \nabla {\mathit{\boldsymbol{u}}^h}} \right) - \nabla \cdot \mathit{\boldsymbol{\sigma }}\left( {{p^h},{\mathit{\boldsymbol{u}}^h}} \right) - \rho \mathit{\boldsymbol{f}}} \right]{\rm{d}}{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}^e} = 0。} \end{array} $ | (22) |
式中:wh和qh分别为速度、压力权函数,uh和ph分别为速度和压力试探解。该方程的前4项为标准Galerkin弱积分形式,其他为由于稳定化方法的引入而增加的稳定项。其中τSUPG和τPSPG为稳定化参数,这里按下式选取
| $ {\tau _{{\rm{SUPG}}}} = {\tau _{{\rm{PSPG}}}} = {\left[ {{{\left( {\frac{{2\left\| {{\mathit{\boldsymbol{u}}^h}} \right\|}}{h}} \right)}^2} + 9{{\left( {\frac{{4\mu }}{{{h^2}}}} \right)}^2}} \right]^{ - \frac{1}{2}}}。$ | (23) |
速度和压力的插值形式为:
| $ {\mathit{\boldsymbol{u}}^h} = \mathit{\boldsymbol{\bar Nv}},\;\;\;\;\;\;\;{p^h} = \mathit{\boldsymbol{N}}p。$ | (24) |
其中:
| $ \mathit{\boldsymbol{\bar N}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{N}}&0&{{\mathit{\boldsymbol{N}}_{{\rm{enr}}}}}&0\\ 0&\mathit{\boldsymbol{N}}&0&{{\mathit{\boldsymbol{N}}_{{\rm{enr}}}}} \end{array}} \right],\;\;\;\;\mathit{\boldsymbol{v}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{U}}\\ {\mathit{\boldsymbol{\hat U}}} \end{array}} \right]。$ | (25) |
式中,N为常规形函数,Nenr为附加形函数,具有如下形式:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{N}} = \left[ {{N_1},{N_2}, \cdots ,{N_n}} \right],}\\ {{\mathit{\boldsymbol{N}}_{{\rm{enr}}}} = \left[ {M_1^ * ,M_2^ * , \cdots ,M_n^ * } \right]。} \end{array} $ | (26) |
这里,U,
| $ \mathit{\boldsymbol{U}} = {\left[ {{u_1},{u_2}, \cdots ,{u_n}} \right]^{\rm{T}}},\;\;\;\;\mathit{\boldsymbol{\hat U}} = {\left[ {{{\hat u}_1},{{\hat u}_2}, \cdots ,{{\hat u}_n}} \right]^{\rm{T}}}。$ | (27) |
以上方程弱解积分式(22)的空间离散形式如下:
| $ \begin{array}{*{20}{c}} {\left( {\mathit{\boldsymbol{M}} + {\mathit{\boldsymbol{M}}_\delta }} \right)\mathit{\boldsymbol{a}} + \mathit{\boldsymbol{C}}\left( \mathit{\boldsymbol{v}} \right) + {\mathit{\boldsymbol{C}}_\delta }\left( \mathit{\boldsymbol{v}} \right) + }\\ {\left( {\mathit{\boldsymbol{K}} + {\mathit{\boldsymbol{K}}_\delta }} \right)\mathit{\boldsymbol{v}} - \left( {\mathit{\boldsymbol{G}} + {\mathit{\boldsymbol{G}}_\delta }} \right)p = }\\ {\left( {\mathit{\boldsymbol{F}} + {\mathit{\boldsymbol{F}}_\delta }} \right){\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{v}} + {\mathit{\boldsymbol{M}}_\varepsilon }\mathit{\boldsymbol{a}} + }\\ {{\mathit{\boldsymbol{C}}_\varepsilon }\left( \mathit{\boldsymbol{v}} \right) + {\mathit{\boldsymbol{K}}_\varepsilon }\mathit{\boldsymbol{v}} + {\mathit{\boldsymbol{G}}_\varepsilon }p = \mathit{\boldsymbol{E}} + {\mathit{\boldsymbol{E}}_\varepsilon }。} \end{array} $ | (28) |
式中:v, a, p分别为速度、速度的时间导数ðv/ðt、压力的节点未知量;M为加速度项;C(v)为对流相关项;K为扩散项;G为压力项;E、F项由边界条件而产生。下标δ,ε分别表示SUPG和PSPG稳定项。
按照文献[13-14]的时间积分方案,假设t+Δt时刻的加速度、速度和压力与t时刻的量有如下关系:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{a}}^{t + \Delta t}} = {\mathit{\boldsymbol{a}}^t} + \Delta \mathit{\boldsymbol{a}},}\\ {\frac{{{\mathit{\boldsymbol{v}}^{t + \Delta t}} - {\mathit{\boldsymbol{v}}^t}}}{{\Delta t}} = \alpha \cdot {\mathit{\boldsymbol{a}}^{t + \Delta t}} + \left( {1 - \alpha } \right) \cdot {\mathit{\boldsymbol{a}}^t},}\\ {{\mathit{\boldsymbol{p}}^{t + \Delta t}} = {\mathit{\boldsymbol{p}}^t} + \Delta \mathit{\boldsymbol{p}}。} \end{array} $ | (29) |
可将式(28)写成如下增量形式求解:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}^ * }\Delta \mathit{\boldsymbol{a}} - {\mathit{\boldsymbol{G}}^ * }\Delta p = \mathit{\boldsymbol{R}},}\\ {{{\left( {{\mathit{\boldsymbol{G}}^{\rm{T}}}} \right)}^ * }\Delta \mathit{\boldsymbol{a}} - \mathit{\boldsymbol{G}}_\varepsilon ^ * \Delta p = \mathit{\boldsymbol{Q}}。} \end{array} $ | (30) |
式中:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{R}} = \mathit{\boldsymbol{F}} + {\mathit{\boldsymbol{F}}_\delta } - \left[ {\left( {\mathit{\boldsymbol{M}} + {\mathit{\boldsymbol{M}}_\delta }} \right)\mathit{\boldsymbol{a}} + \mathit{\boldsymbol{C}}\left( \mathit{\boldsymbol{v}} \right) + } \right.}\\ {\left. {{\mathit{\boldsymbol{C}}_\delta }\left( \mathit{\boldsymbol{v}} \right) + \left( {\mathit{\boldsymbol{K}} + {\mathit{\boldsymbol{K}}_\delta }} \right)\mathit{\boldsymbol{v}} - \left( {\mathit{\boldsymbol{G}} + {\mathit{\boldsymbol{G}}_\delta }} \right)p} \right],}\\ {\mathit{\boldsymbol{Q}} = \mathit{\boldsymbol{E}} + {\mathit{\boldsymbol{E}}_\varepsilon } - \left[ {{\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{v}} + {\mathit{\boldsymbol{M}}_\varepsilon }\mathit{\boldsymbol{a}} + } \right.}\\ {\left. {{\mathit{\boldsymbol{C}}_\varepsilon }\left( \mathit{\boldsymbol{v}} \right) + {\mathit{\boldsymbol{K}}_\varepsilon }\mathit{\boldsymbol{v}} - {\mathit{\boldsymbol{G}}_\varepsilon }p} \right],}\\ {{\mathit{\boldsymbol{M}}^ * } = \mathit{\boldsymbol{M}} + {\mathit{\boldsymbol{M}}_\delta } + \alpha \Delta t\left( {\frac{{\partial \mathit{\boldsymbol{C}}\left( \mathit{\boldsymbol{v}} \right)}}{{\partial \mathit{\boldsymbol{v}}}} + \frac{{\partial {\mathit{\boldsymbol{C}}_\delta }\left( \mathit{\boldsymbol{v}} \right)}}{{\partial \mathit{\boldsymbol{v}}}} + \mathit{\boldsymbol{K}} + {\mathit{\boldsymbol{K}}_\delta }} \right),}\\ {{\mathit{\boldsymbol{G}}^ * } = \mathit{\boldsymbol{G}} + {\mathit{\boldsymbol{G}}_\delta },}\\ {{{\left( {{\mathit{\boldsymbol{G}}^{\rm{T}}}} \right)}^ * } = {\mathit{\boldsymbol{M}}_\varepsilon } + \alpha \Delta t\left( {\frac{{\partial \mathit{\boldsymbol{C}}\left( \mathit{\boldsymbol{v}} \right)}}{{\partial \mathit{\boldsymbol{v}}}} + {\mathit{\boldsymbol{K}}_\varepsilon } + {\mathit{\boldsymbol{G}}^{\rm{T}}}} \right)。} \end{array} $ |
增量方程(30)可迭代求解。在t时刻选择迭代初值
| $ \mathit{\boldsymbol{v}}_0^{t + \Delta t} = {\mathit{\boldsymbol{v}}^t} + \Delta t{\mathit{\boldsymbol{a}}^t},\mathit{\boldsymbol{a}}_0^{t + \Delta t} = {\mathit{\boldsymbol{a}}^t},\mathit{\boldsymbol{p}}_0^{t + \Delta t} = {\mathit{\boldsymbol{p}}^t}, $ | (31) |
代入式(30)求解得到Δa和Δp,并由以下列关系修正各量
| $ \begin{array}{l} \mathit{\boldsymbol{a}}_{i + 1}^{t + \Delta t} = \mathit{\boldsymbol{a}}_i^{t + \Delta t} + \Delta \mathit{\boldsymbol{a}},\\ \mathit{\boldsymbol{v}}_{i + 1}^{t + \Delta t} = \mathit{\boldsymbol{v}}_i^{t + \Delta t} + \Delta t\alpha \Delta \mathit{\boldsymbol{a}},\\ p_{i + 1}^{t + \Delta t} = p_i^{t + \Delta t} + \Delta p。\end{array} $ | (32) |
然后代入式(30)重新计算。以上过程不断迭代直至收敛,进入下一时刻的迭代计算。参数α用来控制时间积分的精度和稳定性,通过改变α值可以得到不同时间积分格式,
针对上述方法,编制了相应的计算程序。下面以2个算例验证本文方法和程序的正确性。
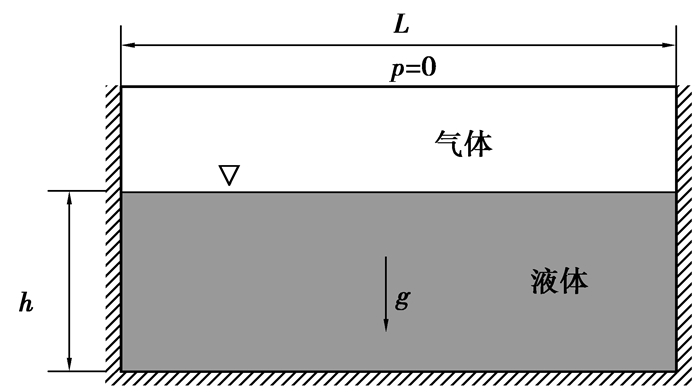
5.1 液体自由晃动问题如图 4所示的1 m×1 m正方形无顶盖容器内装有深度为0.5 m的液体,液体和空气的密度分别为1 000 kg/m3和1 kg/m3,重力加速度g=9.81 m/s2。计算区域采用三角形等参单元离散,单元数为1 200。速度和压力采用同阶线性插值。气液两相交界面的初始形状为λ=a·sin(π(x+0.5)/L), 式中a为波幅,这里取a=0.01 m。在理想流体和微幅波动的假设前提下, 液体在液箱内晃动的波面谐振频率为
|
图 4 液箱内液体晃动计算模型 |
初始时刻及典型时刻的界面形状如图 5所示。图 6给出了采用本文数值模拟方法和线性理论解[18]得到的液箱左右壁面的自由液面起伏的时间变化曲线,可见数值模拟结果和理论解一致,表明本文方法正确有效。
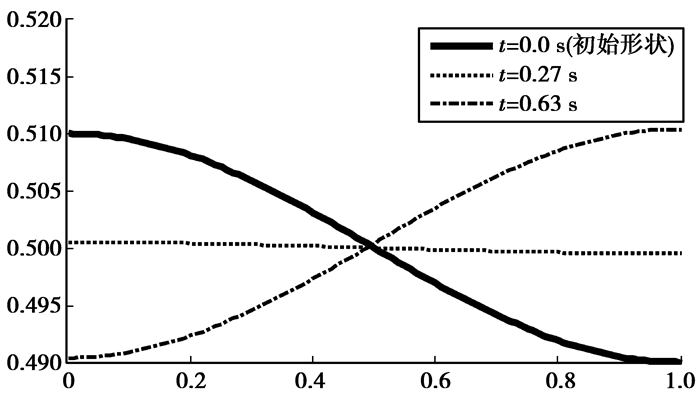
|
图 5 液体晃动液面变化 |
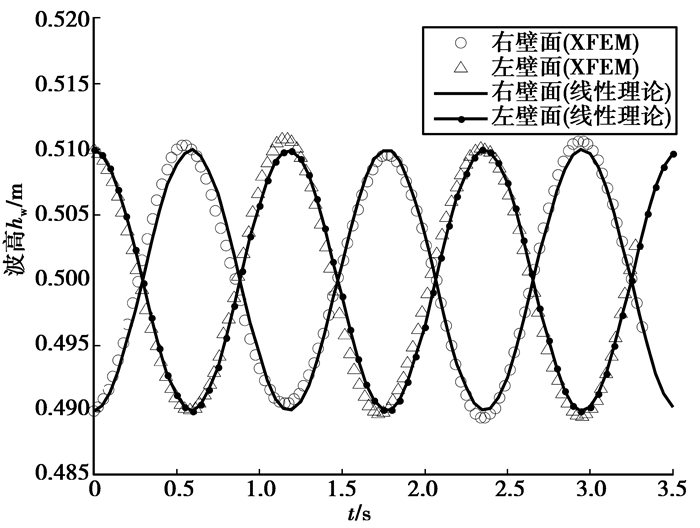
|
图 6 液箱内液体自由晃动数值解与理论解的比较 |
现模拟溃坝流动问题,模型如图 7(a)所示。矩形水柱被固壁和隔板约束,瞬间抽出隔板。固壁边界条件取为滑移条件。水柱初始宽度Z0,H0,且Z0=H0=0.051 75 m。水体的密度和粘性系数分别为1 000 kg/m3和0.001 Pa·s。空气的密度和粘度系数分别为1 kg/m3和1×10-5 Pa·s。分别采用本文扩展有限元方法和有限元法计算分析,均划分4 800个单元。网格如图 7(b)。
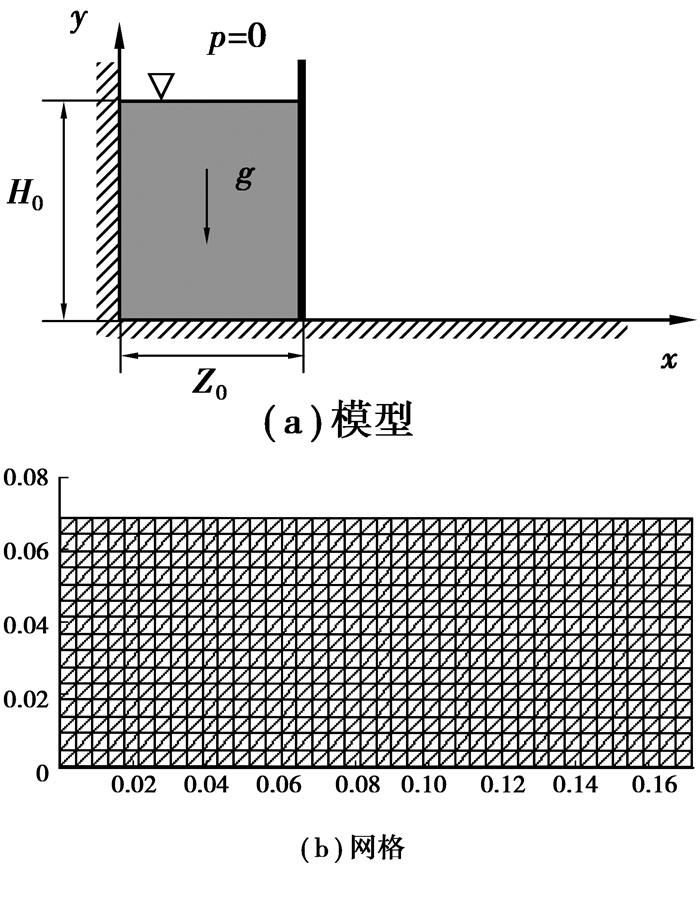
|
图 7 溃坝计算模型及网格划分 |
为比较本文方法和有限元法的结果,引入无量纲时间T1, T2和无量纲位移Z, H:
| $ {T^1} = t\sqrt {\frac{g}{a}} ,{T^2} = t\sqrt {\frac{g}{a}} , $ |
| $ Z = \frac{z}{a},H = \frac{h}{{a{n^2}}}。$ | (40) |
式中:z为水流流到的最前端与初始时刻的距离,h是剩余水柱的高度,g为重力加速度,t为时间。
图 8给出本文方法和FEM方法数值结果与实验结果[19]的比较。可见,在相同网格的情况下,采用本文方法得到的结果与实验数据更接近,比常规有限元方法更有效。另外,随着网格逐渐加密数值结果逐渐趋近于实验数据。且水平集方法能准确捕捉运动界面。
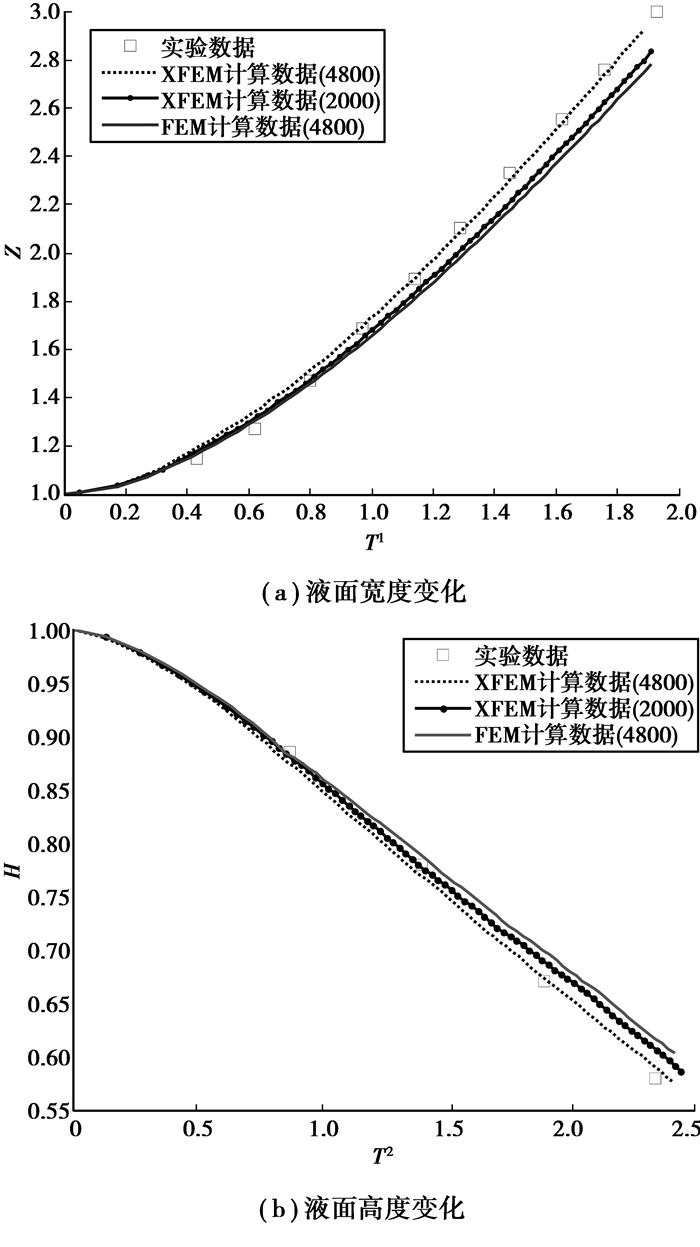
|
图 8 二维溃坝问题数值结果与实验结果的比较 |
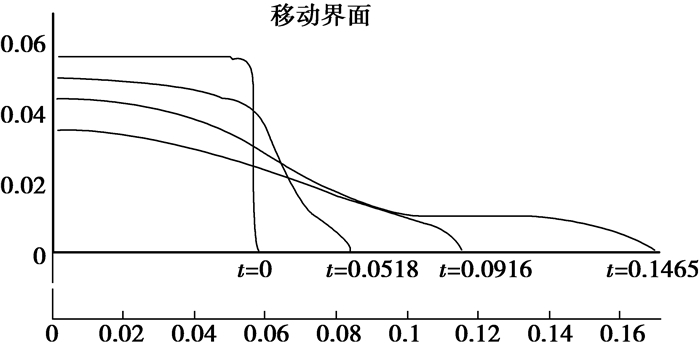
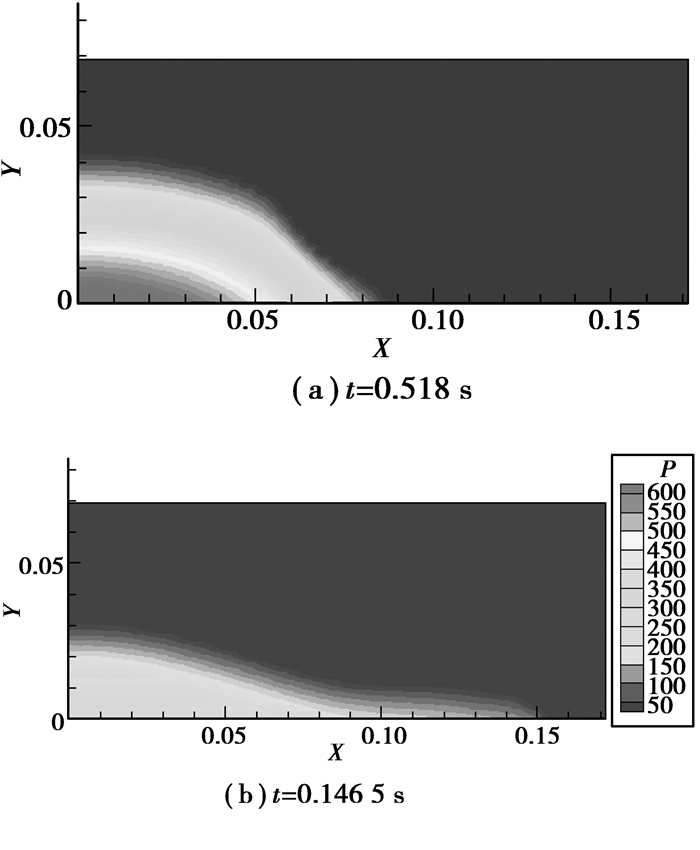
图 9给出采用本文方法计算得到的溃坝后典型时刻两相流界面的变化,图 10所示为典型时刻两相流的压力等值线。
|
图 9 溃坝后两相流界面变化 |
|
图 10 溃坝后压力等值线 |
提出了一种模拟两相流体流动的数值方法,利用修正扩展有限元方法在单元内部考虑两相流界面的非连续性,同时采用水平集法捕获两相流体的移动界面。利用本文方法,在计算过程中无需进行网格重构,而且能够准确捕捉两相流界面的变化。编制了计算程序,通过数值算例验证了本文方法的正确性和有效性。
| [1] | Idelsohn S R, Storti M A, Onate E. Lagrangian formulations to solve free surface incompressible inviscid fluid flows[J]. Computer Methods in Applied Mechanics and Engineering, 2001, 191(6/7): 583–593. |
| [2] | Donea J. Arbitrary lagrangian-eulerian finite element methods[J]. Computational Methods for Transient Analysis, 1983, 1: 473–516. |
| [3] | Hirt C W, Nichols B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of Computational Physics, 1981, 39(1): 201–225. DOI:10.1016/0021-9991(81)90145-5 |
| [4] | Osher S, Sethian J A. Fronts propagating with curvature dependent speed:Algorithms based on Hamilton-Jacobi formulation[J]. Journal of Computer Physics, 1988, 79(1): 12–49. DOI:10.1016/0021-9991(88)90002-2 |
| [5] | Devals C, Heniche M, Bertrand F, et al. A two-phase flow interface capturing finite element method[J]. International Journal for Numerical Methods in fluids, 2007, 53(5): 735–751. DOI:10.1002/(ISSN)1097-0363 |
| [6] | Belytschko T, Black T. Elastic crack growth in finite elements with minimal remeshing[J]. International Journal of Numerical Methods in Engineering, 1999, 46: 131–150. DOI:10.1002/(ISSN)1097-0207 |
| [7] | Melenk J M, Babuška I. The partition of unity finite element method:Basic theory and applications[J]. Computer Methods in Applied Mechanics and Engineering, 1996, 139(1/2/3/4): 289–314. |
| [8] | Fries T P. A corrected XFEM approximation without problems in blending elements[J]. International Journal for Numerical Methods in Engineering, 2008, 75(5): 503–532. DOI:10.1002/nme.v75:5 |
| [9] | Chessa J, Wang H W, Belytschko T. On the construction of blending elements for local partition of unity enriched finite elements[J]. International Journal for Numerical Methods in Engineering, 2003, 57(7): 1015–1038. DOI:10.1002/(ISSN)1097-0207 |
| [10] | Gracie R, Wang H W, Belytschko T. Blending in the extended finite element method by discontinuous Galerkin and assumed strain method[J]. International Journal for Numerical Methods in Engineering, 2008, 74(11): 1645–1669. DOI:10.1002/(ISSN)1097-0207 |
| [11] | Chessa J, Belytschko T. An extended finite element method for two-phase fluids:Flow simulation and modeling[J]. Journal of Applied Mechanics, 2003, 70(1): 10–17. DOI:10.1115/1.1526599 |
| [12] | Fries T P. The intrinsic XFEM for two-fluid flows[J]. International Journal for Numerical Methods in Fluids, 2009, 60(4): 437–471. DOI:10.1002/fld.v60:4 |
| [13] | Tezduyar T E. Stabilized finite element formulations for incompressible flow computations[M]//Hutchinson J W. Advances in applied mechanics. San Diego:Academic Press, Inc., 1992, 28:1-44. |
| [14] | Franca L P, Frey S L. Stabilized finite element methods:Ⅱ. The incompressible Navier-Stokes equations[J]. Computer Methods in Applied Mechanics and Engineering, 1992, 99(2/3): 209–233. |
| [15] | Fries T P. A corrected XFEM approximation without problems in blending elements[J]. International Journal for Numerical Methods in Engineering, 2008, 75(5): 503–532. DOI:10.1002/nme.v75:5 |
| [16] | Peng D P, Merriman B, Osher S, et al. A PDE-based fast local level set method[J]. Journal of Computational Physics, 1999, 155(2): 410–438. DOI:10.1006/jcph.1999.6345 |
| [17] | Sussmann M, Fatemi E, Smereka P, et al. An improved level set method for incompressible two-phase flows[J]. Computers & Fluids, 1998, 27(5/6): 663–680. |
| [18] | Nakayama T, Washizu K. The boundary element method applied to the analysis of two dimensional nonlinear sloshing problems[J]. International Journal for Numerical Methods in Engineering, 1981, 17(11): 1631–1646. DOI:10.1002/(ISSN)1097-0207 |
| [19] | Martin J, Moyce W J. An experimental study of the collapse of liquid columns on a rigid horizontal plane[J]. Philosophical Transactions of the Royal Society of London, 1952, 244(882): 312–324. DOI:10.1098/rsta.1952.0006 |
 2013, Vol. 36
2013, Vol. 36

