2. 中国汽车工程研究院股份有限公司 汽车噪声振动和安全技术国家重点实验室, 重庆 400039
2. State Key Laboratory of Vehicle NVH and Safety Technology, China Automotive Engineering Research Institute Co., Ltd., Chongqing 400039, China
线性MIMO系统的Luenberger规范型广泛的应用于系统的极点配置、状态反馈控制以及线性MIMO系统的状态观测器的设计。
国内外关于Luenberger规范型的研究已经有相当长的时间,也取得了很多成果。早期的文献中对于Luenberger规范型的研究大都集中于完全能控MIMO系统的Luenberger能控规范型[1-10]。其中Luenberger给出了完全能控系统化为Luenberger能控规范型的方法和步骤,但却没有对Luenberger能观规范型进行讨论[1-4]。Kalman[5-6]对线性系统的能控性和能观性进行了分析。Gilbert[7]讨论了线性多变量系统的能控性和能观性及其相互关系,而没有具体探讨完全能观系统的规范型的结构。Jiang等[10]讨论了其规范型实现的充分必要条件,但也仅限于完全能控系统,并没有对能观系统进行讨论。最近的一些文献[11-15]按照对偶原理通过对能控规范型的结构的分析给出了相应的Luenberger能观规范型应该具有的基本结构特征,但是这种方法仅限于完全能控且完全能观系统,对于不完全能控系统并不适用。
总之,对于Luenberger规范型的研究起步很早,各个方面的研究已经也相当的成熟,但是还存在以下几个方面的不足。
首先,Luenberger能观规范型实现的充分必要条件。当前对于Luenberger规范型的研究集中于Luenberger能控规范型的实现及其应用,相关文献指出只有在特定的条件下一个完全能控系统才能够变换为Luenberger能控规范型[10],但是却鲜有文献对Luenberger能观规范型的实现的充要条件研究。其次,完全能观MIMO系统Luenberger能观规范型的实现方法。如果一个系统满足Luenberger能观测规范型实现的条件,其具体实现方法是一个必须要解决的问题。当前文献中对于将MIMO系统化为Luenberger能控规范型有一整套的方法和步骤[1-6],但是却没有对Luenberger能观规范型的实现方法和实现步骤给出任何的结论。第三,Luenberger能观规范型的结构特殊性及产生机理的分析。公开发表的文献中对于Luenberger能观规范型的定义有着细微的差异[1, 10-12],这些差异主要体现在其结构上,但并没有任何文献对这些差异及其形成的原因进行比较和分析。
针对上述问题,首先从完全能观线性MIMO系统时域理论出发,提出了一种线性系统能观测矩阵的线性无关行向量的搜索方案。其次,在此行向量搜索方案的基础之上提出了一种变换矩阵的构造方法,进而对系统的Luenberger能观规范型结构特征及其与变换矩阵的关系进行了分析。根据Luenberger能观规范型的结构特征,提出了将系统的Luenberger能观规范型按照结构的差异分为广义和狭义2种观点,给出了这2种能观规范型实现的充要条件以及狭义Luenberger能观规范型的实现的一个充分条件,同时提出了一种实现方法使得一类不满足Luenberger能观规范型实现条件的线性MIMO系统能够在不改变系统物理结构的前提下变换为Luenberger能观规范型,最后通过5个实例分别对上述观点和方法进行了验证,计算结果表明作者提出观点和实现方法是合理和可行的。
1 能观矩阵线性无关行向量的搜索方案当前关于能观矩阵的线性无关行向量组的搜索方法的研究却很少,一些文献中只是说明其搜索方法与能控矩阵的搜索方法存在“对偶”关系[4],但是却没有能够对这种“对偶”关系的给出具体的解释。作者在对前人研究工作的基础上对能观矩阵进行深入的研究,提出了一种能观矩阵的无关向量组的搜索方案,并给出了具体的步骤。
1.1 研究对象及其基本假设考虑连续时间线性MIMO系统{A,B,C},其状态空间描述为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{Ax}} + \mathit{\boldsymbol{Bu}},}\\ {\mathit{\boldsymbol{y}} = \mathit{\boldsymbol{Cx}},} \end{array} $ |
其中A为n×n系统矩阵,B为n×p控制矩阵,C=[c1T…cpT]T为q×n输出矩阵,且其秩满足rank(C)=m≤q,其中ci,i=1,2,…,q表示C的行向量。表系统的能观矩阵为
| $ {\mathit{\boldsymbol{Q}}_o} = {\left[ {{\mathit{\boldsymbol{C}}^{\rm{T}}}{{\left( {\mathit{\boldsymbol{CA}}} \right)}^{\rm{T}}} \cdots {{\left( {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{A}}^{n - 1}}} \right)}^{\rm{T}}}} \right]^{\rm{T}}}。$ |
基本假设:系统{A,B,C}为连续时间线性时不变系统,且完全能观。即矩阵A,B,C中的元素均为常数,而且系统{A,B,C}的能观测矩阵Qo的秩满足条件rank(Qo)=n。
1.2 能观矩阵线性无关行向量的搜索方案由于矩阵Qo满秩,所以该矩阵有且仅有n个线性无关的行向量。建立如下所示表格,表格由若干行和若干列组成,表格的第i行第j列元素代表由ci与Aj的乘积ciAj,1≤i≤p,1≤j≤n。可以看出,该表格的元素对应于矩阵Qo的各个行向量。
| 表 1 能观测矩阵行向量搜索方案图 |
具体的搜索步骤如下:
Step 1 由于rank(C)=m≤q,所以C中必有且仅有m个线性无关的行向量。对表格第一列,如果c1不为零,则保留c1,否则划去c1,从上至下找出m个线性无关行向量并保留对应的元素,其余的划去。假设经过这一步剩余的这m个行向量分别处于第一列的第i1,i2,…,im行上,并表这m个行向量为ci1,ci2,…,cim。
Step 2 转入第二列,对于i1,i2,…,im这些行的元素从上至下进行搜索。对每一格,判断其对应行向量与先前得到的线性无关行向量组是否线性相关,若线性相关则保留该元素,否则划去该元素。并且,如果已经划去某一个栅格,则所在行中位于其右边的所有行向量必然与先前得到的线性无关行向量为线性相关,就不再需要对相应行中的向量进行搜索,故将其全部划去。
Step 3 转入第三列,对于第三列的i1,i2,…,im这些行的元素从上至下进行搜索。对需要搜索的每一元素,判断其对应行向量与先前得到的线性无关行向量组是否线性相关,若线性相关则保留该该元素,否则划去该元素。
Step 4 采取与第三步类似的方法对其后的列进行搜索,直到找到第n个线性无关的行向量,搜索结束。搜索结束后的表格的示意图如下图所示,实际情况应该根据具体计算结果得出。
| 表 2 能观测矩阵行向量搜索结果图 |
表格中所有保留的元素对应的行向量的总体就是Qo的n个线性无关的行向量。进而对于表格中的各行,用νik来表示第ik行中保留的栅格的个数,根据能观指数集的定义[11]可知{νi1,νi2,…,νim}就是系统的能观指数集。
2 非奇异变换矩阵的构造若系统{A,B,C}的输出矩阵C的前m个行向量为线性无关,则可以通过上述搜索方案,找出能观性矩阵Qo的n个线性无关的行向量,并组成非奇异矩阵
| $ \mathit{\boldsymbol{L}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{L}}_1}}\\ \vdots \\ {{\mathit{\boldsymbol{L}}_{{\nu _m}}}} \end{array}} \right],{\mathit{\boldsymbol{L}}_i} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{C}}_i}}\\ {{\mathit{\boldsymbol{C}}_i}\mathit{\boldsymbol{A}}}\\ \vdots \\ {{\mathit{\boldsymbol{C}}_i}{\mathit{\boldsymbol{A}}^{{\nu _i} - 1}}} \end{array}} \right],i = 1,2, \cdots ,m。$ |
表{ν1,ν2,…νm}为系统的能观指数集,设矩阵L的逆矩阵为L-1=[F1,F2,…,Fm],其中Φi=[fi1,fi2,…,fiνi]为n×νi矩阵;i=1,…,m,则有
| $ {\mathit{\boldsymbol{L}}_i}{\mathit{\boldsymbol{F}}_i} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{C}}_i}{\mathit{\boldsymbol{f}}_{i1}}}& \cdots &{{\mathit{\boldsymbol{C}}_i}{\mathit{\boldsymbol{f}}_{i{\nu _i}}}}\\ \vdots&\cdots&\vdots \\ {{\mathit{\boldsymbol{C}}_i}{\mathit{\boldsymbol{A}}^{{\nu _i} - 1}}{\mathit{\boldsymbol{f}}_{i1}}}& \cdots &{{\mathit{\boldsymbol{C}}_i}{\mathit{\boldsymbol{A}}^{{\nu _i} - 1}}{\mathit{\boldsymbol{f}}_{i{\nu _i}}}} \end{array}} \right] = {\mathit{\boldsymbol{I}}_{{\nu _i} \times {\nu _i}}}, $ | (1) |
其中Iνi×νi为νi×νi单位矩阵。
| $ {\mathit{\boldsymbol{L}}_i}{\mathit{\boldsymbol{F}}_j} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{C}}_i}{\mathit{\boldsymbol{f}}_{j1}}}& \cdots &{{\mathit{\boldsymbol{C}}_i}{\mathit{\boldsymbol{f}}_{j{\nu _i}}}}\\ \vdots&\cdots&\vdots \\ {{\mathit{\boldsymbol{C}}_i}{\mathit{\boldsymbol{A}}^{{\nu _i} - 1}}{\mathit{\boldsymbol{f}}_{j1}}}& \cdots &{{\mathit{\boldsymbol{C}}_i}{\mathit{\boldsymbol{A}}^{{\nu _i} - 1}}{\mathit{\boldsymbol{f}}_{j{\nu _j}}}} \end{array}} \right] = {\mathit{\boldsymbol{O}}_{{\nu _i} \times {\nu _j}}}, $ | (2) |
其中i≠j,Oνi×νj为νi×νj零矩阵。
构造矩阵T=[T1…Tm],称为变换矩阵,其中Ti=[fiνi,Afiνi,…,Aνi-1fiνi]为n×νi矩阵(i=1,2,…,m)。
引理1 矩阵T=[T1 … Tm]非奇异。
证明:假设存在一组数k11,…k1(ν1-1),…,km(νm-1)使得
| $ \sum\limits_{i = 1}^m {\left( {{k_{i1}}{\mathit{\boldsymbol{f}}_{i{\nu _i}}} + {k_{i2}}A{\mathit{\boldsymbol{f}}_{i{\nu _i}}} + \cdots + {k_{i{\nu _i}}}{\mathit{\boldsymbol{A}}^{{\nu _i} - 1}}{\mathit{\boldsymbol{f}}_{i{\nu _i}}}} \right)} = 0, $ | (3) |
将式(3)两端各乘以Ci,利用式(1)和式(2),得到kiνiCiAνi-1fiνi=kiνi=0,i=1,2,…,m。
将式(3)两端各乘以CiA,利用上面得到的结果将kiνi=0带入,同样利用式(1)和式(2),得到ki(νi-1)CiAνi-1fiνi=ki(νi-1)=0,i=1,2…,m。
然后依次以CiA2,CiA3,…,CiAνi-1乘以式(3)的两端,并利用前一次的结果,最终可以得到
| $ {k_{i1}} = {k_{i2}} = \cdots = {k_{i{\nu _i}}} = 0,i = 1,2, \cdots ,m。$ |
可以看出组成矩阵T的各个行向量线性无关,所以矩阵T为非奇异矩阵,定理证毕。
3 Luenberger能观规范型实现的条件及结构特征Luenberger能观规范型的实现其实就是通过寻找一种非奇异变换矩阵,将其变换为Luenberger能观规范型的表示形式。当前公开发表的文献中,对于线性系统Luenberger能观规范型的定义分为两种[1, 9-11],这两种定义有一些细微的差别,但是这两种细微的差别造成了其实现条件有很大的不同。通过定理1和定理2来阐述Luenberger能观规范型的基本结构特征。然后通过定理3引入广义和狭义Luenberger能观规范型的概念,分别讨论了其实现的充要条件,并对问题进行了进一步的探讨,提出了狭义Luenberger能观规范型实现的一个充分条件。
3.1 Luenberger能观规范型的结构特征定理1 对于系统{A,B,C},若矩阵C的前m个行向量线性无关,则可构造非奇异矩阵T,使得T-1AT=Ã,且Ã具有以下特殊形式

|
Iνi-1表示νi-1维单位矩阵,Oνi×(νj-1)表示νi×(νj-1)维零矩阵,*表示矩阵的元素没有特殊性,要根据具体情况进行计算。
证明 将n×n矩阵Ã按照如下方式分块
| $ \sum\limits_{i = 1}^m {\sum\limits_{k = 1}^{{\nu _i}} {a_{ks}^{ij}{\mathit{\boldsymbol{A}}^{k - 1}}{\mathit{\boldsymbol{f}}_{i{\nu _i}}} = {\mathit{\boldsymbol{A}}^s}{\mathit{\boldsymbol{f}}_{j{\nu _j}}}} } ,1 \le j \le m,1 \le s \le {\nu _j} $ |
1) 当1≤s≤νj-1时,有
| $ \sum\limits_{i = 1,i \ne j}^m {\sum\limits_{k = 1}^{{\nu _i}} {a_{ks}^{ij}{\mathit{\boldsymbol{A}}^{k - 1}}{\mathit{\boldsymbol{f}}_{i{\nu _i}}}} } + \sum\limits_{k = 1}^{{\nu _j}} {a_{ks}^{ij}{\mathit{\boldsymbol{A}}^{k - 1}}{\mathit{\boldsymbol{f}}_{j{\nu _j}}}} = {\mathit{\boldsymbol{A}}^s}{\mathit{\boldsymbol{f}}_{j{\nu _j}}}。$ |
将等式右边移到左边后合并同类项得到
| $ \begin{array}{*{20}{c}} {\sum\limits_{i = 1,i \ne j}^m {\sum\limits_{k = 1}^{{\nu _i}} {a_{ks}^{ij}{\mathit{\boldsymbol{A}}^{k - 1}}{\mathit{\boldsymbol{f}}_{i{\nu _i}}}} } + \sum\limits_{k = 1,k \ne s + 1}^{{\nu _j}} {a_{ks}^{jj}{\mathit{\boldsymbol{A}}^{k - 1}}{\mathit{\boldsymbol{f}}_{j{\nu _j}}}} + }\\ {\left( {a_{\left( {s + 1} \right)s}^{jj} - 1} \right){\mathit{\boldsymbol{A}}^s}{\mathit{\boldsymbol{f}}_{j{\nu _j}}} = 0。} \end{array} $ |
考虑到f1ν1,Af1ν1,…,Aν1-1f1ν1,…,Aνm-1fmνm为线性无关向量组,所以当i≠j时aksij=0;当i=j时,aksjj=0,k≠s+1,a(s+1)sjj=1。
2) 当s=νj时,有
| $ \sum\limits_{i = 1}^m {\sum\limits_{k = 1}^{{\nu _i}} {a_{k{\nu _j}}^{ij}{\mathit{\boldsymbol{A}}^{k - 1}}{\mathit{\boldsymbol{f}}_{i{\nu _i}}} - {\mathit{\boldsymbol{A}}^{{\nu _j}}}{\mathit{\boldsymbol{f}}_{j{\nu _j}}}} } = 0。$ |
由于f1ν1,Af1ν1,…,Aν1-1f1ν1,…,Aνm-1fmνm线性无关,而f1v1,Af1ν1,…,Aν1-1f1ν1,…,Aνm-1fmνm,Aνjfjνj线性相关向量组,根据线性代数理论,方程组(4)的解akνjij,1≤i≤m,1≤k≤νi存在且唯一。
综合以上的结论,可以将矩阵Ãij表示如下
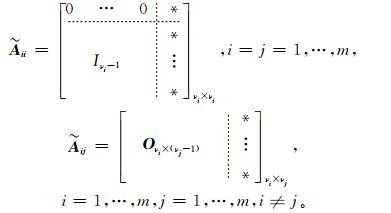
|
定理证毕。
定理2 对于系统{A,B,C},若矩阵C的前m个行向量线性无关,则存在非奇异矩阵T,使得
1) 当1≤i<j≤m时
| $ {{\mathit{\boldsymbol{\tilde C}}}_{ij}} = {\mathit{\boldsymbol{C}}_i}{\mathit{\boldsymbol{T}}_j} = {\left[ {0, \cdots ,0} \right]_{1 \times {\nu _j}}}。$ |
2) 当j=i,i=1,…,m时
| $ {{\mathit{\boldsymbol{\tilde C}}}_{ii}} = {\mathit{\boldsymbol{C}}_i}{\mathit{\boldsymbol{T}}_i} = {\left[ {0, \cdots 0,1} \right]_{1 \times {\nu _i}}} = {\left[ {0, \cdots 0,1} \right]_{1 \times {\nu _j}}}。$ |
3) 当m≥i>j≥1时
| $ {{\mathit{\boldsymbol{\tilde C}}}_{ij}} = {\mathit{\boldsymbol{C}}_i}{\mathit{\boldsymbol{T}}_j} = \left\{ \begin{array}{l} {\left[ {0, \cdots ,0} \right]_{1 \times {\nu _j}}},{\nu _i} \ge {\nu _j}\\ {\left[ {0, \cdots ,0,{t_{ij}}} \right]_{1 \times {\nu _j}}},{\nu _i} \le {\nu _j} - 1 \end{array} \right.。$ |
其中tij表示此元素的值不一定为零,要根据具体情况进行计算。
证明:
1) 当i<j时,若νi≥νj,由LiFj=Oνi×νj得到Cifjνj=…=CiAνi-1fjνj=0,所以可以得到CiTj=[0,…,0]1×vj。若νi<νj,则同样由LiFj=Oνi×νj得到Cifjνj=…=CiAνi-1fjνj=0。由于矩阵L的n个行向量是采用搜索方法的步骤,用来表示CiAk,νi≤k≤νj-1的线性无关向量中不包含向量CjAνj-1。考虑到矩阵L中除了CjAνj-1之外其它的行向量均满足与fjνj正交,所以CiAkfjνj=0,νi≤k≤νj-1。所以CiTj的各个元素均为0,即CiTj=[0,…,0]1×vj。
2) 当i=j时,CiTi=[Cifi1,…,CiAνi-1fiνi]1×vi由于LiFi=Iνi×νi,所以CiAk-1fik=0,1≤k≤νi,即CiTi=[0,…0,1]1×vi=[0,…0,1]1×vj。
3) 当i>j时
若νi≥νj,由Cifjνj=…=CiAνi-1fjνj=0,可知CiTj的各个元素均为0,即CiTj=[0,…,0]1×vj。
若νi<νj即νi≤νj-1,首先由LiFj=Oνi×νj知Cifjνj=…=CiAνi-1fjνj=0。其次,根据搜索方案的特性对于CiAk,νi≤k≤νj-2这些行向量来说,用来线性表示这些向量的线性无关向量组中不包含向量CjAνj-1,而用来表示CiAνj-1的线性无关行向量中必然包含CjAνj-1。由于矩阵L中的行向量除了CjAνj-1之外其它的均与fjνj正交,而对于CjAνj-1满足CjAνj-1fjνj=1。用tij来表示CiAνj-1的所有线性无关向量中CjAνj-1的系数,则对于CiAk,当νi≤k≤νj-2时满足CiAkfjνj=0,而CiAνj-1fjνj=tij,即CiTj=[0,…,0,tij]1×νj。定理证毕。
3.2 广义和狭义Luenberger能观规范型实现的充要条件定理3 对于完全能观线性时不变系统{A,B,C},rank(C)=m≤q,如果矩阵C的前m行为线性无关,即此系统输出矩阵C中顺序最大线性无关行向量组所含向量个数等于矩阵C的秩。那么存在线性非奇异变换x=T
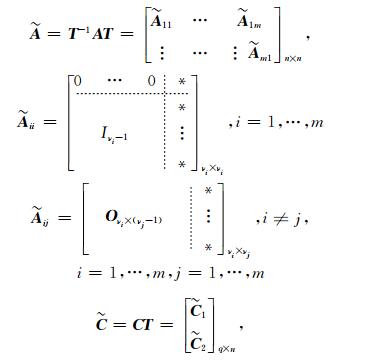
|
| $ {{\mathit{\boldsymbol{\tilde C}}}_{ii}} = {\left[ {\begin{array}{*{20}{c}} 0& \cdots &0&1 \end{array}} \right]_{1 \times {\nu _i}}},i = 1, \cdots ,m, $ |
| $ {{\mathit{\boldsymbol{\tilde C}}}_{ij}} = {\left[ {0, \cdots ,0} \right]_{1 \times {\nu _j}}},i < j,i = 1, \cdots ,m, $ |
| $ {{\mathit{\boldsymbol{\tilde C}}}_{ij}} = \left\{ \begin{array}{l} {\left[ {0, \cdots ,0} \right]_{1 \times {\nu _j}}},i > j,{\nu _i} \ge {\nu _j}\\ {\left[ {0, \cdots ,0,{t_{ij}}} \right]_{1 \times {\nu _j}}},i > j,{\nu _i} \le {\nu _j} - 1, \end{array} \right. $ |
i=1, …,m, tij表示此元素的值不一定为零。
证明:
必要性:若系统{A,B,C}的输出矩阵C的前m行线性无关,则可以按照提出的方法和步骤构造出非奇异变换矩阵T=[T1 … Tm]。然后根据定理1和定理2即可证明变换后的系统矩阵和输出矩阵具有上述的形式。
充分性:如果系统能够通过非奇异变换矩阵化为Luenberger能观规范型,则系统的输出矩阵的秩与变换前系统输出矩阵的秩相同,即rank
相关文献中把定理3中的系统{
若对于定理三的系统{
定理4 对于完全能观线性时不变系统{A,B,C},rank(C)=m≤q,能够将此系统化为狭义Luenberger能观规范型的充要条件是:
1) 矩阵C的前m行为线性无关,即此系统输出矩阵C中顺序最大线性无关行向量组所含向量个数等于矩阵C的秩。
2) 对于系统{A,B,C}及其能观测指数集{ν1,ν2,…,νm},当i>j,且νi≤νj-1时,用来表示CiAνj-1的线性无关向量中CjAνj-1的系数必须为零,即tij=0。
3.3 狭义Luenberger能观规范型实现的充分条件由于定理4的条件非常的苛刻,所以对于系统{A,B,C},它的狭义Luenberger能观测规范型一般是不存在的。但是笔者通过研究发现,如果系统{A,B,C}的能观测矩阵Qo的线性无关行向量的搜索方案能够使得该系统的能观测指数满足一定的条件,那么该系统的狭义Luenberger能观规范型就一定存在。
定理5 对于完全能观线性时不变系统{A,B,C},rank(C)=m≤q,如果满足定理3的条件的同时,按照提出的搜索方案搜索能观测矩阵的线性无关行向量时,搜索结果使得其能观测指数还满足ν1≤ν2≤…≤νm,那么必可以将该系统化为狭义Luenberger能观规范型。
证明 首先根据定理3,利用所提出的实现方法一定可以将系统{A,B,C}化为广义Luenberger能观规范型。
如果系统{A,B,C}的能观测指数还满足ν1≤ν2≤…≤νm,那么根据定理3的结论有:
通过3个实例的分析对作者在上一节所提出的观点和方法进行了验证。继而提出了一个新的方法将不满足定理3的线性MIMO系统变换为Luenberger能观规范型,并用另2个实例验证了该方法正确性和可行性。
例1:对于如下线性MIMO系统{A,B,C},判断其Luenberger能观规范型是否存在,若不存在说明原因,若存在将其化为Luenberger能观规范型。
| $ \mathit{\boldsymbol{\dot x}} = \left[ {\begin{array}{*{20}{c}} 0&1&1&0&0&0\\ 1&2&0&0&0&0\\ 0&0&1&{ - 2}&0&1\\ 0&{ - 2}&1&0&1&1\\ 0&0&0&1&0&0\\ 0&0&0&0&0&1 \end{array}} \right]\mathit{\boldsymbol{x}} + \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&2&3\\ 1&{ - 2}&3\\ 1&2&4\\ { - 1}&{ - 2}&3\\ 1&0&{ - 2} \end{array}} \right]\mathit{\boldsymbol{u}}, $ |
| $ \mathit{\boldsymbol{y}} = \left[ {\begin{array}{*{20}{c}} 0&2&0&0&0&0\\ 0&1&0&0&0&0\\ 0&1&0&1&0&1\\ 1&2&0&0&0&0\\ 0&2&0&1&0&1 \end{array}} \right]\mathit{\boldsymbol{x}}。$ |
解:首先计算出该系统的能观测矩阵Qo的秩为rank(Qo)=6,由此判断该系统为完全能观。矩阵C的秩为:rank(C)=3,但是矩阵C的前3行为线性相关,即
| $ {\rm{rank}} = \left( {\left[ {\begin{array}{*{20}{c}} 0&2&0&0&0&0\\ 0&1&0&0&0&0\\ 0&1&0&1&0&1 \end{array}} \right]} \right) = 2 \ne {\rm{rank}}\left( \mathit{\boldsymbol{C}} \right)。$ |
根据定理3,由于该系统的输出矩阵C的前3行线性相关,所以其广义和狭义Luenberger能观规范型是不存在的。换句话说,一个系统如果连广义Luenberger能观测规范型存在的条件都无法满足的话,则其狭义Luenberger规范型肯定不存在。
例2:对于如下线性MIMO系统{A,B,C},判断其Luenberger能观规范型是否存在,若不存在说明原因,若存在则将其化为Luenberger能观规范型。
| $ \mathit{\boldsymbol{\dot x}} = \left[ {\begin{array}{*{20}{c}} 0&1&1&0&0&0\\ 1&2&0&0&0&0\\ 0&0&1&{ - 2}&0&1\\ 0&{ - 2}&1&0&1&1\\ 0&0&0&1&0&0\\ 0&0&0&0&0&1 \end{array}} \right]\mathit{\boldsymbol{x}} + \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&2&3\\ 1&{ - 2}&3\\ 1&2&4\\ { - 1}&{ - 2}&3\\ 1&0&{ - 2} \end{array}} \right]\mathit{\boldsymbol{u}}, $ |
| $ \mathit{\boldsymbol{y}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&0&0\\ 0&1&0&0&0&0\\ 0&1&0&1&0&1\\ 1&2&0&0&0&0\\ 0&2&0&1&0&1 \end{array}} \right]\mathit{\boldsymbol{x}}。$ |
解:首先计算出该系统的能观测矩阵Qo的秩为rank(Qo)=6,所以该系统完全能观。矩阵C的秩为rank(C)=3,而且前3行线性无关,即
| $ {\rm{rank}}\left( {\left[ {\begin{array}{*{20}{c}} 1&0&0&0&0&0\\ 0&1&0&0&0&0\\ 0&1&0&1&0&1 \end{array}} \right]} \right) = 3 = {\rm{rank}}\left( \mathit{\boldsymbol{C}} \right)。$ |
根据定理3该系统的广义Luenberger能观规范型存在。利用所提出的该系统的能观测矩阵Qo的关行向量的搜索方案,最终确定其线性无关行向量为:C1,C1A,C1A2,C2,C3,C3A,所以该系统的能观测数为:v1=3,v2=1,v3=2。但是由于v3>v2,根据定理4可知该系统的狭义Luenberger能观规范型不存在。根据第二小节所提出的构造方法,构造出非奇异变换矩阵T为
| $ \mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} 0&0&1&0&0&0\\ 0&0&0&1&0&0\\ 0&1&2&{ - 1}&0&0\\ { - \frac{1}{3}}&{ - \frac{1}{3}}&1&0&0&1\\ { - \frac{2}{3}}&{ - \frac{1}{3}}&{ - \frac{1}{3}}&3&1&0\\ {\frac{1}{3}}&{\frac{1}{3}}&{\frac{1}{3}}&{ - 1}&0&0 \end{array}} \right]。$ |
最终得到变换后的系统{

|
变换后的系统{
可以看出狭义Luenberger能观规范型是广义Luenberger能观测规范型的特殊情况,能够变换为狭义Luenberger能观规范型的系统,肯定是满足其广义Luenberger规范型存在的充要条件的,但是一个系统如果满足了广义Luenberger能观规范型存在的条件,其狭义Luenberger能规范型也不一定存在,要看其是否满足进一步的条件即定理4或者定理5所提出的条件。
例3:对于如下线性MIMO系统{A,B,C},判断其Luenberger能观规范型是否存在,若不存在说明原因,若存在将其化为Luenberger能观规范型。
| $ \mathit{\boldsymbol{\dot x}} = \left[ {\begin{array}{*{20}{c}} 0&1&1&0&0&0\\ 1&{ - 2}&0&0&0&0\\ 0&0&1&{ - 2}&0&1\\ 0&1&1&0&1&1\\ 0&0&0&1&0&0\\ 0&0&0&0&0&0 \end{array}} \right]\mathit{\boldsymbol{x}} + \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&2&1\\ 1&{ - 2}&3\\ 1&0&4\\ { - 1}&2&0\\ 1&0&{ - 2} \end{array}} \right]\mathit{\boldsymbol{u}}, $ |
| $ \mathit{\boldsymbol{y}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&0&0\\ 0&1&{ - 1}&0&0&0\\ 0&1&0&1&0&1\\ 0&{ - 1}&{ - 1}&0&0&0\\ 0&1&0&1&0&1 \end{array}} \right]\mathit{\boldsymbol{x}}, $ |
解:首先判断该系统为完全能观。矩阵C的秩为rank(C)=3,而且其前三行为线性无关,即
| $ {\rm{rank}}\left( {\left[ {\begin{array}{*{20}{c}} 1&0&0&0&0&0\\ 0&1&{ - 1}&0&0&0\\ 0&1&0&1&0&1 \end{array}} \right]} \right) = 3 = {\rm{rank}}\left( \mathit{\boldsymbol{C}} \right)。$ |
根据定理3可知系统的广义Luenberger能观规范型存在。根据提出的方法确定系统能观测矩阵Qo线性无关行向量为:C1,C1A,C2,C2A,C3,C3A,所以该系统的能观测数为:v1=v2=v3=2。进而根据定理五可知该系统的狭义Luenberger规范型存在,根据所提出的构造方法,构造出非奇异变换矩阵T为
| $ \mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} 0&1&0&0&0&0\\ {\frac{1}{2}}&{ - 1}&0&0&0&0\\ {\frac{1}{2}}&{ - 1}&0&{ - 1}&0&0\\ {\frac{1}{3}}&1&{\frac{1}{3}}&0&0&1\\ {\frac{5}{6}}&{\frac{1}{3}}&{\frac{1}{3}}&{\frac{1}{3}}&1&0\\ { - \frac{5}{6}}&0&{ - \frac{1}{3}}&0&0&0 \end{array}} \right], $ |
最终得到变换后的系统{
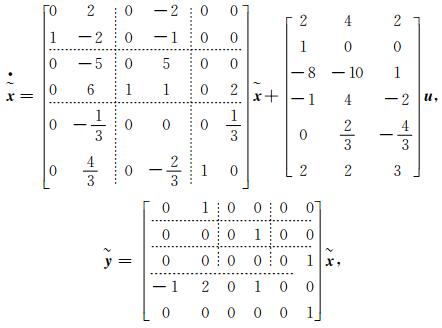
|
可以看出,系统{
事实上对于一般的系统,很难保证输出矩阵C的前m个行向量线性无关,这时根据定理3,该系统连广义Luenberger能观规范型都不存在。但是,由于系统的状态空间描述只是对研究对象的一种描述方法,如果从状态变量和输出变量的选择顺序上来看,同一个对象的状态空间描述能够有很多种,这样就可以换一种状态空间描述方式,将其变换为Luenberger能观规范型。
定理6 对于完全能观系统{A,B,C},如果矩阵C的秩为rank(C)=m,但是其前m个行向量线性相关,那么就通过初等行变换将其前m个行向量线性无关,状态空间描述上表示为将系统的输出方程两端各左乘以一个初等换法矩阵,物理上相当于对系统输出向量的各个输出分量进行重新编号,实际并未改变系统,其过程如下图所示
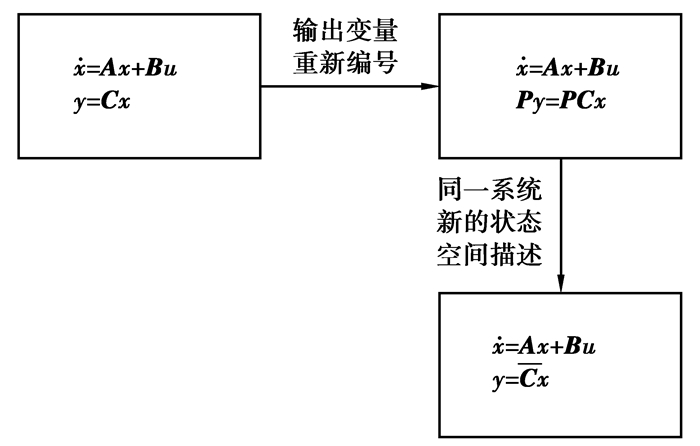
|
图 1 同一物理系统的不同状态空间描述 |
由于此变换不改变其系统的能观测性,系统{A,B,C}同样是是完全能观测的,所以可以将该系统化为Luenberger能观测规范型。
例4:对于例1中的系统{A,B,C},该系统虽然完全能观,但是由于其输出矩阵C的结构不满足定理3的条件,其Luenberger能观规范型是不存在的。问能否通过对输出矩阵C进行合理的换行,将换行后的系统变换为Luenberger能观规范型。
解:由于rank(C)=3,所以存在非奇异矩阵P,使得PC=C,且C的前3行为线性无关。选取矩阵P为
| $ \mathit{\boldsymbol{P}} = \left[ {\begin{array}{*{20}{c}} 0&1&0&0&0\\ 0&0&1&0&0\\ 0&0&0&1&0\\ 1&0&0&0&0\\ 0&0&0&0&1 \end{array}} \right]。$ |
此时的系统{A,B,C}可以表示为
| $ \mathit{\boldsymbol{\dot x}} = \left[ {\begin{array}{*{20}{c}} 0&1&1&0&0&0\\ 1&2&0&0&0&0\\ 0&0&1&{ - 2}&0&1\\ 0&{ - 2}&1&0&1&1\\ 0&0&0&1&0&0\\ 0&0&0&0&0&1 \end{array}} \right]\mathit{\boldsymbol{x}} + \left[ {\begin{array}{*{20}{c}} 1&0&0\\ 0&2&3\\ 1&{ - 2}&3\\ 1&2&4\\ { - 1}&{ - 2}&3\\ 1&0&{ - 2} \end{array}} \right]\mathit{\boldsymbol{u}}, $ |
| $ \mathit{\boldsymbol{\bar y}} = \left[ {\begin{array}{*{20}{c}} 0&1&0&0&0&0\\ 0&1&0&1&0&1\\ 1&2&0&0&0&0\\ 0&2&0&0&0&0\\ 0&2&0&1&0&1 \end{array}} \right]\mathit{\boldsymbol{x}}。$ |
根据定理3系统{A,B,C}的广义Luenberger能观规范型存在,按照前述的方法确定其线性无关行向量为:C1,C2,C2A,C2A2,C3,C3A,即该系统的能观测数为:v1=1,v2=3,v3=2,但是由于v2>v1,根据定理4可知该系统的狭义Luenberger能观规范型不存在。根据所提出的构造方法,构造出非奇异变换矩阵T为
| $ \mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} { - 2}&0&0&{\frac{3}{4}}&0\\ 1&0&0&0&0\\ { - 1}&0&{\frac{3}{4}}&{\frac{3}{2}}&1\\ { - 1}&{ - \frac{1}{4}}&{ - \frac{1}{4}}&{\frac{3}{4}}&{\frac{1}{2}}\\ 3&{ - \frac{1}{2}}&{ - \frac{1}{2}}&{ - \frac{1}{2}}&0\\ 0&{\frac{1}{4}}&{\frac{1}{4}}&{\frac{1}{4}}&{ - \frac{1}{2}} \end{array}} \right]。$ |
最终得到变换后的系统{
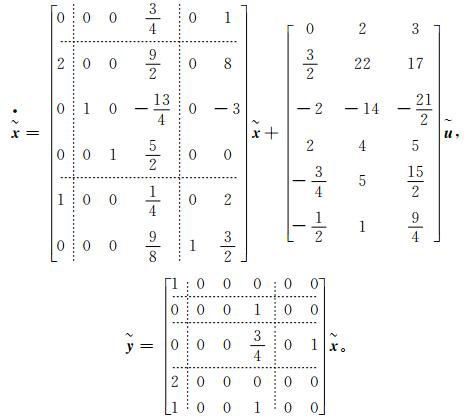
|
可以看出,系统{
例5:对于例1中的系统{A,B,C},选取与例4不同的初等行变换矩阵P,并将换行后的系统变换为其Luenberger能观规范型。
解:选取初等行变换矩阵P为
| $ \mathit{\boldsymbol{P}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&0\\ 0&0&1&0&0\\ 0&0&0&1&0\\ 0&1&0&0&0\\ 0&0&0&0&1 \end{array}} \right], $ |
此时,变换后的系统的状态矩阵和控制矩阵都与例4相同,其输出矩阵C为
| $ \mathit{\boldsymbol{\bar C}} = \left[ {\begin{array}{*{20}{c}} 0&2&0&0&0&0\\ 0&1&0&1&0&1\\ 1&2&0&0&0&0\\ 0&1&0&0&0&0\\ 0&2&0&1&0&1 \end{array}} \right], $ |
按照前几个例子的计算步骤,最终确定其线性无关行向量为:C1,C2,C2A,C2A2,C3,C3A,进而根据所提出的构造方法,构造出非奇异变换矩阵T为
| $ \mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} { - 1}&0&0&{\frac{3}{4}}&0&1\\ {\frac{1}{2}}&0&0&0&0&0\\ { - \frac{1}{2}}&0&{\frac{3}{4}}&{\frac{3}{2}}&1&{ - \frac{1}{2}}\\ { - \frac{1}{2}}&{ - \frac{1}{4}}&{ - \frac{1}{4}}&{\frac{3}{4}}&{\frac{1}{2}}&{\frac{1}{2}}\\ {\frac{3}{2}}&{ - \frac{1}{2}}&{ - \frac{1}{2}}&{ - \frac{1}{2}}&0&{\frac{1}{2}}\\ 0&{\frac{1}{4}}&{\frac{1}{4}}&{\frac{1}{4}}&{ - \frac{1}{2}}&{ - \frac{1}{2}} \end{array}} \right]。$ |
最终得到变换后的系统{
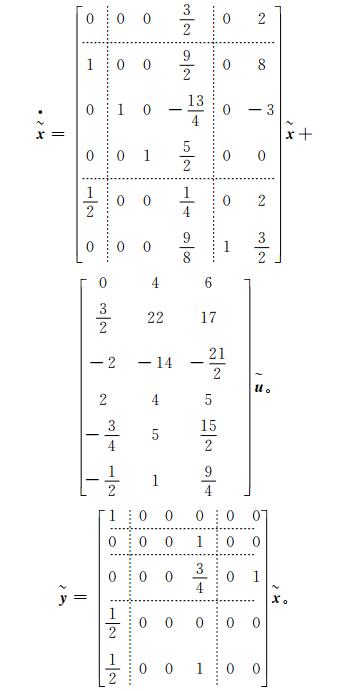
|
可以看出,该系统的结构与例4的结构有着较大的差异,但是实际上这2种状态空间描述都对应着同一个物理对象。
5 结论从线性MIMO系统时域理论出发,提出了一种线性系统能观测矩阵的线性无关行向量的搜索方案,并在此行向量搜索方案的基础之上提出了变换矩阵的构造方法,进而对系统的Luenberger能观规范型结构特征及其与变换矩阵的关系进行了分析,根据Luenberger能观规范型的结构特征,提出了将系统的Luenberger能观规范型按照结构的差异分为广义和狭义2种的观点,给出了这2种能观规范型实现的充要条件以及狭义Luenberger能观规范型的实现的一个充分条件并做了详细的证明,并通过3个实例的分析和比较对作者所提出的观点和实现方法进行了验证。进而给出了当系统不满足Luenberger能观规范型实现的条件时,在不改变物理系统的前提下,可以通过改变输出变量顺序来改变系统的状态空间描述,从而使得变换后的系统满足Luenberger能观规范型实现的条件的方法,并通过两个实例的分析和比较阐述了该方法的有效性。
| [1] | Luenberger D G. Canonical forms for linear multivariable systems[J]. IEEE Transactions on Automatic Control, 1967, 12(3): 290–293. DOI:10.1109/TAC.1967.1098584 |
| [2] | Luenberger D G. Observers for multivariable systems[J]. IEEE Transactions on Automatic Control, 1966, 11(2): 190–197. DOI:10.1109/TAC.1966.1098323 |
| [3] | Luenberger D G. An introduction to observers[J]. IEEE Transactions on Automatic Control, 1971, 16(6): 596–603. DOI:10.1109/TAC.1971.1099826 |
| [4] | Kalman R E. Canonical structure of linear dynamic systems[J]. Proceedings of the National Academy of Sciences of United States of America, 1962, 48(4): 596–600. DOI:10.1073/pnas.48.4.596 |
| [5] | Kalman R E, Ho Y C, Narendra K S. Controllability of linear dynamical systems[J]. Contributions to Differential Equations, 1961, 1(3): 189–213. |
| [6] | Kalman R E. Mathematical descriptions of linear dynamical systems[J]. Journal of the Society for Industrial and Applied Mathematics, Series A:Control, 1963, 1(2): 152–192. DOI:10.1137/0301010 |
| [7] | Gilbert E. Controllability and observability in multivariable control systems[J]. Journal of the Society for Industrial and Applied Mathematics, Series A:Control, 1963, 2(1): 128–151. |
| [8] | Morgan B S Jr. The synthesis of linear multivariable systems by state-variable feedback[J]. IEEE Transactions on Automatic Control, 1964, 9(4): 405–411. DOI:10.1109/TAC.1964.1105733 |
| [9] | Luo Z. Transformations between canonical forms for multivariable linear constant systems[J]. IEEE Transactions on Automatic Control, 1977, 22(2): 252–256. DOI:10.1109/TAC.1977.1101488 |
| [10] |
江宁强, 宋文忠.
MIMO系统转化为Luenberger能控规范型的条件[J]. 控制理论与应用, 2007, 24(5): 866–868.
JIANG Ningqiang, SONG Wenzhong. Restraint on MIMO system in being transformed into the Luenberger's canonical form[J]. Control Theory and Applications, 2007, 24(5): 866–868. (in Chinese) |
| [11] | 郑大钟. 线性系统理论[M]. 2版. 北京: 清华大学出版社, 2005. |
| [12] | 刘豹. 现代控制理论[M]. 2版. 北京: 机械工业出版社, 2005. |
| [13] |
韩肖宁, 董达生.
线性系统能控性和能观性的几何判据:核空间、象空间、不变子空间的基本概念[J]. 电力学报, 2008, 23(1): 21–25.
HAN Xiaoning, DONG Dasheng. The geometric criteria on controllability and observability of linear system:the basic concept of kernel space, image space and invariant space[J]. Journal of Electric Power, 2008, 23(1): 21–25. (in Chinese) |
| [14] | Petersen I R. A kalman decomposition for robustly unobservable uncertain linear systems[J]. Systems and Control Letters, 2008, 57(10): 800–804. DOI:10.1016/j.sysconle.2008.03.005 |
| [15] | Pruneda R E, Solares C, Conejo A J, et al. An efficient algebraic approach to observability analysis in state estimation[J]. Electric Power System Research, 2010, 80(3): 277–286. DOI:10.1016/j.epsr.2009.09.010 |
 2013, Vol. 36
2013, Vol. 36


