由于抑制传动噪声、提高接触寿命的需要，精密齿轮越来越多地采用拓扑修形螺旋曲面。拓扑修形螺旋面一般采用三轴联动成形磨削进行精加工，即在螺旋线运动轨迹上附加径向或切向等运动以适应修形的螺旋线^[1]，但易产生齿面扭曲缺陷，影响齿面加工质量^[2-4]。五轴成形磨齿机更多的加工自由度为解决齿面扭曲、提高磨削精度提供了更大的可能性。然而，要充分发挥五轴磨齿机的潜力，必须解决砂轮扫掠体包络面的有效计算问题，以便为砂轮轨迹优化、磨削精度评估和磨削仿真等功能实现提供算法支撑。

对于一般回转刀具在五坐标运动下的扫掠体包络面的计算，2002年前提出的多是数值法^[5]，如Jacobi秩亏损方法、Blackmore扫掠微分方程方法、Minkowski和方法、隐式建模方法等，数值法需要求解高阶常微分方程或超越方程，计算量很大。近年来，刀具包络面的解析计算方法研究取得了很大进展。CHIOU等^[6]提出了一种五轴端铣加工APT刀具扫掠轮廓表达式。DU等^[7]在此基础上进行了扩展应用。GONG等^[8]基于活动标架方法，给出了一般回转刀具包络面的两种解析表达式。ARAS^[9]提出了回转刀具包络面的双参数球族包络表示方法。ZHU等^[10-11]基于单参数曲面族包络原理，给出了一般回转面在任意刚体运动下的扫掠体包络面的解析表达式，并基于双参数球族包络原理，建立了柱刀、锥刀、鼓形刀和环刀等刀具的包络面解析表达式。Senatore等^[12]基于刀具包络面的解析表达进行了刀具路径的优化。

解析法已成为回转刀具包络面计算的主流方法，足以表达柱刀、锥刀、环刀及鼓形刀等常规刀具的包络面，但在表达磨齿砂轮这种形状复杂刀具的包络面时能力不足。另外，五轴成形磨齿机结构也不同于常规的五轴加工中心，需针对其结构进行运动几何学分析^[13]。为此，文中提出了双参数点矢量族包络法，通过分析其几何特性，实现基于砂轮点矢量的特征点计算。并进一步结合五轴磨齿机的运动分析，实现基于磨齿数控代码的砂轮包络面计算，并给出了计算实例。

1 双参数点矢量族包络

砂轮五轴成形磨削原理为单参数曲面族包络原理。根据刚体运动学，在$\mathbb{R}^3 $中，回转曲面可看成母线作圆周运动形成的轨迹曲面(母线族)，故砂轮单参数曲面族包络可看成母线双参数运动(回转运动+包络运动)包络而成。当从母线上取出一点进行包络计算时，为了不丢失该点的几何信息，点应表达为位置加方向矢量的形式，即点矢量。此时，单参数回转曲面族包络可看成母线上多个点矢量的双参数运动包络，文中称之为双参数点矢量族包络。

1.1 砂轮母线的点矢量离散

成形磨齿砂轮形状远比常规铣削刀具复杂。在实际齿轮磨削编程中，为方便砂轮的数控修整，一般要将计算出的砂轮点拟合成由多段直线和圆弧构成的组合曲线^[14-15]。根据直线及圆弧在砂轮母线中的分布情况，砂轮可看作由多个柱刀(直线)、锥刀(斜线)、圆环刀(小圆弧)、鼓形刀(圆弧外凸)、双曲线刀(圆弧内凹)等组合而成的复杂刀具。

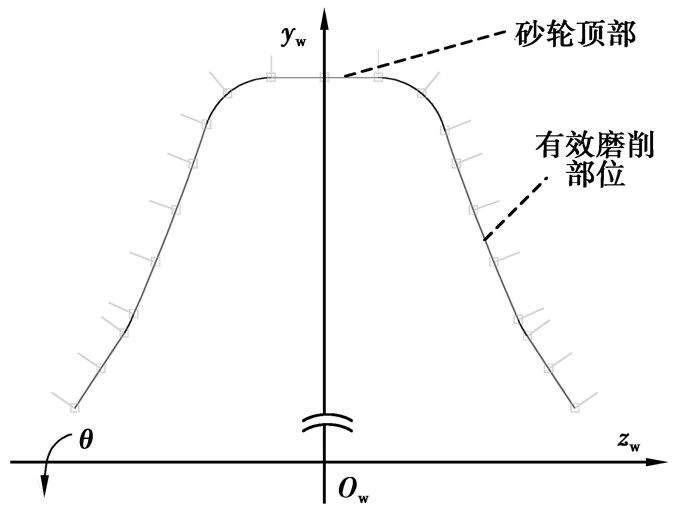
具体算法可参见笔者前期提出的点矢量离散法^[16]，即将直线、圆弧采用几何数据(距离、弧度或角度)平均化来建立离散准则，得到几何意义上分布均匀的离散点。直线上各个离散点的法向矢量相等，而圆弧上离散点的法向矢量由其自身指向圆心。图 1为由圆弧和直线组成的砂轮母线点矢量离散示意图，点矢量的法线方向用等长直线表示。在点矢量离散时，除砂轮母线几何平均点处外，分段点处也默认生成一个点矢量。

1.2 双参数点矢量族包络的几何特性

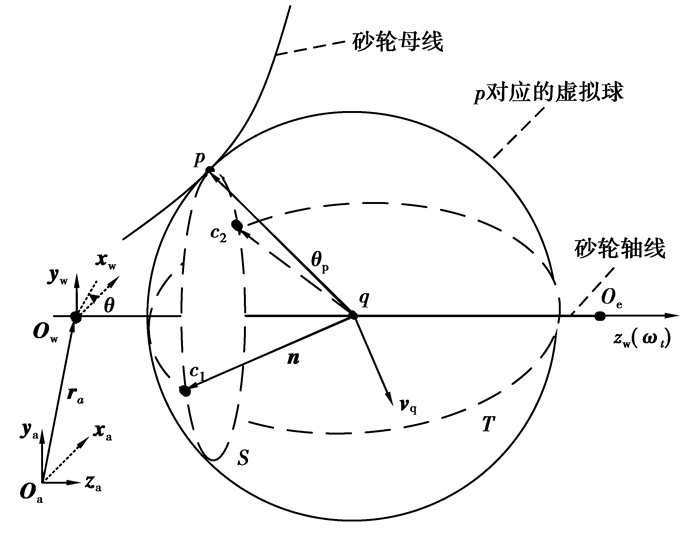
为研究双参数点矢量族的包络特性，建立图 2所示的2个坐标系，CS_a={O_a；x_a，y_a，z_a}为惯性坐标架，CS_w={O_w；x_w，y_w，z_w}为活动坐标架，砂轮轴上的一个固定点O_w为坐标原点，z_w轴与砂轮轴重合。r_t为O_w在惯性坐标架中的表达。为简化包络计算，下面在活动坐标架中求取特征点。

在时刻t的刀位，点矢量p的双参数运动，一为绕砂轮轴线的旋转运动ω_t，另一个为砂轮的包络运动。旋转运动ω_t形成砂轮回转曲面的纬线圆S，p对应的特征点必位于纬线圆上。由旋转曲面的微分几何特性可知，若回转曲面在p点处纬线圆的法线与砂轮轴线相交于点q，则p点处纬线圆曲率半径为‖qp‖，q为曲率中心，曲面在纬线圆上任意一点处的法线始终由q指向该点。

根据包络理论，特征点应满足的包络条件为

$ \mathit{\boldsymbol{v}} \cdot \mathit{\boldsymbol{n}} = 0。$

(1)

不同时刻纬线圆包络运动形成的纬线圆族可表达为

$ {\mathit{\boldsymbol{r}}_{\rm{f}}}\left( {\theta ,t} \right) = {\mathit{\boldsymbol{r}}_t}\left( t \right) + \left\| {{O_{\rm{w}}}q} \right\|{\mathit{\boldsymbol{z}}_{\rm{w}}}\left( t \right) + \left\| {qp} \right\|\mathit{\boldsymbol{n}}\left( {\theta ,t} \right), $

(2)

式中，r_f为与θ、t相关的函数，将式(2)对t求导，得到纬线圆速度矢量

$ \begin{array}{l} \mathit{\boldsymbol{v}} = \frac{{{\rm{d}}{\mathit{\boldsymbol{r}}_{\rm{f}}}\left( {\theta ,t} \right)}}{{{\rm{d}}t}} = \\ \;\;\;\;\;\;\frac{{{\rm{d}}\left( {{\mathit{\boldsymbol{r}}_t} + \left\| {{O_{\rm{w}}}q} \right\|{\mathit{\boldsymbol{z}}_{\rm{w}}}} \right)}}{{{\rm{d}}t}} + \left\| {qp} \right\|\frac{{{\rm{d}}\mathit{\boldsymbol{n}}}}{{{\rm{d}}t}}。\end{array} $

(3)

将式(3)代入式(1)，得

$ \begin{array}{l} \mathit{\boldsymbol{v}} \cdot \mathit{\boldsymbol{n}} = \left( {\frac{{{\rm{d}}\left( {{\mathit{\boldsymbol{r}}_t} + \left\| {{O_{\rm{w}}}q} \right\|{\mathit{\boldsymbol{z}}_{\rm{w}}}} \right)}}{{{\rm{d}}t}} + \left\| {qp} \right\|\frac{{{\rm{d}}\mathit{\boldsymbol{n}}}}{{{\rm{d}}t}}} \right) \cdot \mathit{\boldsymbol{n}} = \\ \;\;\;\;\;\;\;\;\frac{{{\rm{d}}\left( {{\mathit{\boldsymbol{r}}_t} + \left\| {{O_{\rm{w}}}q} \right\|{\mathit{\boldsymbol{z}}_{\rm{w}}}} \right)}}{{{\rm{d}}t}} \cdot \mathit{\boldsymbol{n}} = \\ \;\;\;\;\;\;\;\;{\mathit{\boldsymbol{v}}_q} \cdot \mathit{\boldsymbol{n}} = 0。\end{array} $

(4)

由式(4)可知，特征点处曲面法向矢量与特征点对应的曲率中心处的速度矢量的标积为0。从几何意义上解读，特征点为纬线圆与通过点q且垂直于v_q的平面的交点。为便于形象分析和描述特征点，可认为母线上任何一个点矢量p都唯一对应着一个虚拟球，虚拟球参数包括：虚拟球心q、球半径‖qp‖以及法向矢量qp。

从点矢量双参数运动角度看，旋转运动ω_t形成纬线圆S；包络运动形成截圆T，它为过虚拟球心q且与v_t垂直的平面与虚拟球相交而得。因此特征点可看作纬线圆与截圆的交点。

1.3 特征点计算的解析表达

如图 2所示，设点p在CS_w中坐标为(0，y_p，z_p)，点p对应的虚拟球参数：球心q (0，0，z_p+y_p/tanφ)、球半径‖y_p/sin φ‖，其中φ为法线矢量qp与z_w轴的夹角。纬线圆圆心为(0，0，z_p)，半径为y_p，纬线圆所在平面的法向矢量为z_w，在活动标架CS_w中可表示为

$ \mathit{\boldsymbol{r}}{\left( \theta \right)^{\left( {\rm{w}} \right)}} = {y_p}\cos \theta {\mathit{\boldsymbol{x}}_{\rm{w}}} + {y_p}\sin \theta {\mathit{\boldsymbol{y}}_{\rm{w}}} + {z_p}{\mathit{\boldsymbol{z}}_{\rm{w}}}, $

(5)

则p点所在纬线圆上任一点的法向矢量为

$ \begin{array}{l} \mathit{\boldsymbol{n}}{\left( \theta \right)^{\left( {\rm{w}} \right)}} = \mathit{\boldsymbol{r}}{\left( \theta \right)^{\left( {\rm{w}} \right)}} - {\mathit{\boldsymbol{O}}_{\rm{w}}}{\mathit{\boldsymbol{q}}^{\left( {\rm{w}} \right)}} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;{y_p}\left( {\cos \theta {\mathit{\boldsymbol{x}}_{\rm{w}}} + \sin \theta {\mathit{\boldsymbol{y}}_{\rm{w}}} - \frac{1}{{\tan \varphi }}{\mathit{\boldsymbol{z}}_{\rm{w}}}} \right)。\end{array} $

(6)

虚拟球心q的速度在CS_w中可表示为

$ \mathit{\boldsymbol{v}}_q^{\left( {\rm{w}} \right)} = {v_1}{\mathit{\boldsymbol{x}}_w} + {v_2}{\mathit{\boldsymbol{y}}_w} + {v_3}{\mathit{\boldsymbol{z}}_w}。$

(7)

将式(6)、式(7)带入式(4)，得

$ {v_1}\cos \theta + {v_2}\sin \theta = {v_3}/\tan \varphi 。$

(8)

解方程(8)，得

$ {\theta _{1,2}} = {\tan ^{ - 1}}\left( {\frac{{{v_2} \pm \sqrt \Delta }}{{{v_1} + {v_3}/\tan \varphi }}} \right), $

(9)

式中，Δ=v₁²+v₂²-v₃²/tan²φ。

当Δ＞0时，可求得2个特征点，如图 2所示的c₁、c₂；当Δ=0时，纬线圆与截圆交于一点，只有一个特征点c，如图 3(a)所示；当Δ＜0时，纬线圆与截圆没有交点，不存在特征点，如图 3(b)所示。

当点矢量p的虚拟球参数及虚拟球心速度v_q^(w)都已知后，可由式(9)求得θ值，再代入式(5)中，即可求得特征点在活动坐标架中的值。

因此，虚拟球参数及球心速度的求解，是双参数点矢量族包络法应用的前提，下面进行具体讨论。

2 虚拟球参数及虚拟球心速度的计算 2.1 砂轮母线上点矢量对应的虚拟球参数

由于砂轮母线是由多段直线和圆弧构成的组合曲线，下面分别讨论直线和圆弧上点矢量虚拟球参数计算方法。

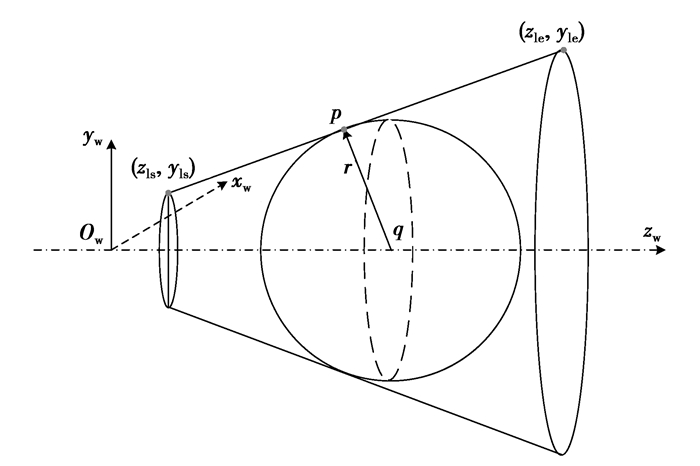
2.1.1 直母线上点矢量对应的虚拟球参数

砂轮直母线部分对应的回转曲面为圆锥面。如图 4所示直母线首末点为(z_ls，y_ls)、(z_le，y_le)，其上点矢量p对应的虚拟球球心为q。

在平面y_wO_wz_w内，直母线上点的法向矢量大小处处相等，为${n_{\rm l}} = - \frac{{{z_{{\rm{le}}}} - {z_{{\rm{ls}}}}}}{{{y_{{\rm{le}}}} - {y_{{\rm{ls}}}}}} $。点的法向矢量qp与z_w夹角为φ_l=atan(n_l)，虚拟球心q坐标为(0，0，z_p-y_p/n_l)，球半径r=‖y_p/sin φ_l‖。

当y_ls=y_le，即直母线与砂轮轴线平行时，回转曲面为一圆柱面，此时法向矢量垂直于砂轮轴线，虚拟球心为(0，0，z_p)，球半径为‖y_p‖。

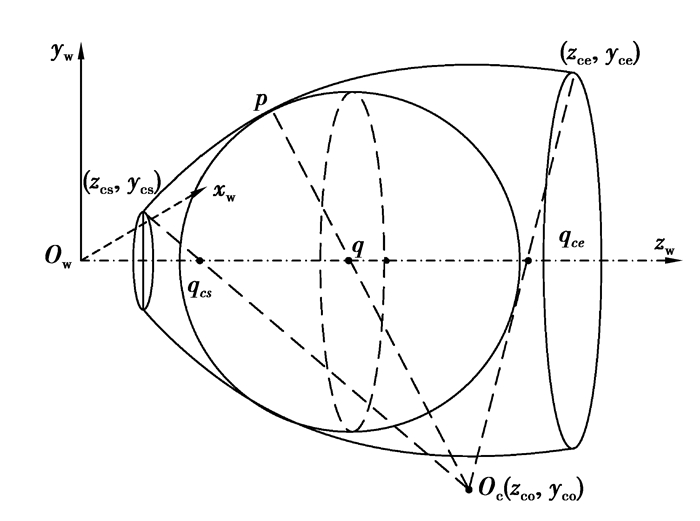
2.1.2 圆弧母线上点矢量对应的虚拟球参数

砂轮圆弧母线部分对应的回转曲面为鼓形面。图 5所示圆弧母线首末点为(z_cs，y_cs)、(z_ce，y_ce)，圆心为(z_co，y_co)，其上点矢量p对应的虚拟球球心为q。

圆弧上任一点p(z_p，y_p)处的法向矢量为${\boldsymbol{n}_c} = - \frac{{{y_p} - {y_{{\rm{co}}}}}}{{{z_p} - {z_{{\rm{co}}}}}} $，与z_w夹角为φ_c=atan(n_c)。虚拟球心q坐标为(0，0，z_p-y_p/n_c)，球半径为r=‖y_p/sin φ_c‖。

当y_p=y_co，此时法向矢量垂直于砂轮轴，虚拟球心为(0，0，z_p)，球半径为‖y_p‖。

2.2 虚拟球心速度

现有针对铣削回转刀具的包络计算方法，一般要给出刀具轴线上两点的运动轨迹^[3]，文中为方便数控磨齿仿真，讨论基于磨齿数控程序的包络计算。假设在惯性坐标架中参考点处速度为v₀，砂轮轴角速度为ω，则q点在惯性坐标架中的速度为

$ \mathit{\boldsymbol{v}}_q^{\left( {\rm{a}} \right)} = {\mathit{\boldsymbol{v}}_0} + {z_q}\mathit{\boldsymbol{\omega }}。$

(10)

v_q^(a)与v₀及ω相关，需要根据NC代码求参考点的速度v₀及砂轮轴角速度ω。对于笛卡儿直角坐标系类型机床，参考点的线性运动速度在惯性坐标架中可表示为

$ \left( {{\mathit{\boldsymbol{v}}_0}} \right)_i^{\left( {\rm{a}} \right)} = \left( {{v_{0x}}} \right)_i^{\left( {\rm{a}} \right)}{\mathit{\boldsymbol{x}}_{\rm{a}}} + \left( {{v_{0y}}} \right)_i^{\left( {\rm{a}} \right)}{\mathit{\boldsymbol{y}}_{\rm{a}}} + \left( {{v_{0z}}} \right)_i^{\left( {\rm{a}} \right)}{\mathit{\boldsymbol{z}}_a}, $

(11)

式中，$ \left\{ \begin{array}{l} \left( {{v_{0x}}} \right)_i^{\left( {\rm{a}} \right)} = \frac{{{{\left( {{x_t}} \right)}_{i + 1}} - {{\left( {{x_t}} \right)}_i}}}{{\Delta t}},\\ \left( {{v_{0y}}} \right)_i^{\left( {\rm{a}} \right)} = \frac{{{{\left( {{y_t}} \right)}_{i + 1}} - {{\left( {{y_t}} \right)}_i}}}{{\Delta t}},\\ \left( {{v_{0x}}} \right)_i^{\left( {\rm{a}} \right)} = \frac{{{{\left( {{z_t}} \right)}_{i + 1}} - {{\left( {{z_t}} \right)}_i}}}{{\Delta t}}。\end{array} \right.$(i=1，2，…，N-1)，

由于速度具体值对包络计算结果没有影响，式(11)中可令Δt=1以简化(v₀)_i^(a)的计算。

同样，角速度ω在惯性坐标架中可表达为

$ \mathit{\boldsymbol{\omega }}_i^{\left( {\rm{a}} \right)} = \left( {{\omega _x}} \right)_i^{\left( {\rm{a}} \right)}{\mathit{\boldsymbol{x}}_a} + \left( {{\omega _y}} \right)_i^{\left( {\rm{a}} \right)}{\mathit{\boldsymbol{y}}_a} + \left( {{\omega _z}} \right)_i^{\left( {\rm{a}} \right)}{\mathit{\boldsymbol{z}}_a}。$

(12)

式中，$ \left\{ \begin{array}{l} \left( {{\omega _x}} \right)_i^{\left( {\rm{a}} \right)} = \frac{{{A_{i + 1}} - {A_i}}}{{\Delta t}},\\ \left( {{\omega _y}} \right)_i^{\left( {\rm{a}} \right)} = \frac{{{B_{i + 1}} - {B_i}}}{{\Delta t}},\\ \left( {{\omega _z}} \right)_i^{\left( {\rm{a}} \right)} = \frac{{{C_{i + 1}} - {C_i}}}{{\Delta t}}。\end{array} \right.$(i=1，2，…，N-1)，

仍令Δt=1，以保持与速度同样的计算比例系数。通过式(11)、式(12)可计算惯性坐标架中的v₀及ω。

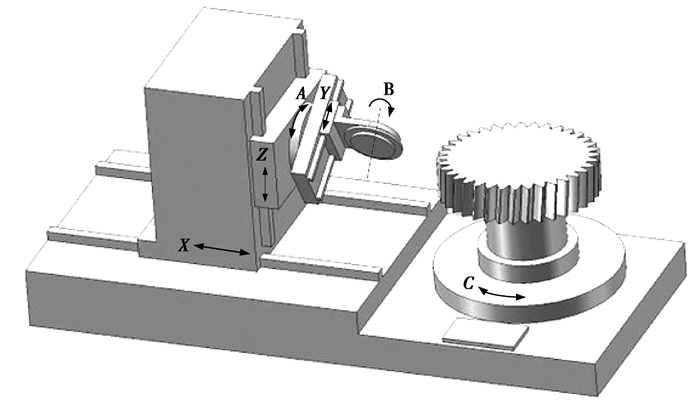
3 五轴成形磨齿机坐标系及坐标变换 3.1 磨齿机坐标系建立及坐标变换

图 6为典型的五轴联动CNC成形磨齿机示意图，它包含3个直线运动轴(X，Y，Z)及2个旋转轴(A，C)。B轴(砂轮自身的旋转运动)不参与坐标联动。数控加工编程时，A为砂轮的摆动角度，C为齿轮的旋转角度，Z为砂轮齿轴方向进给量，Y为砂轮齿切方向进给量，X为砂轮齿深方向进给量。与普通笛卡尔直角坐标类型的数控机床不同，典型磨齿机Y向与X向及Z向通常情况下不能构成一个直角坐标系，但这种立式机床结构刚性好，在磨削大齿轮时形变小，能保证磨削精度。

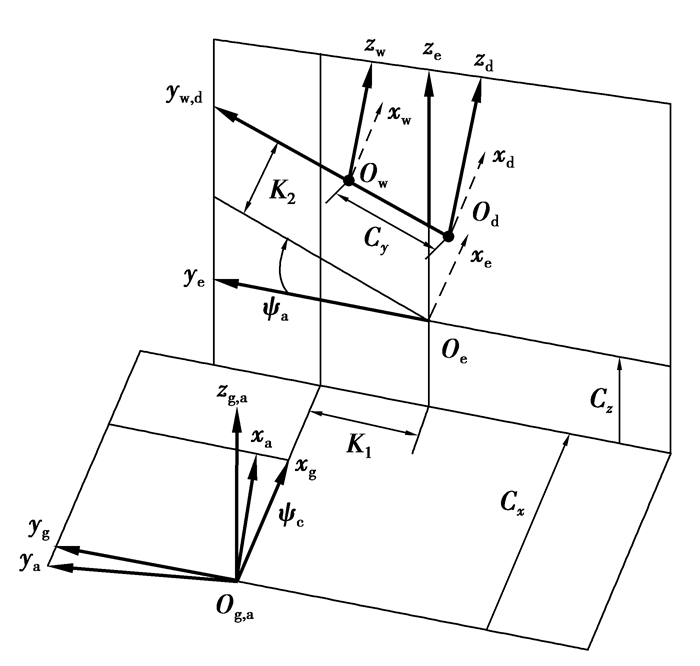
为便于运动分析和计算，建立图 7所示的CS_g、CS_a、CS_w 3个坐标系，其中CS_a={O_a；x_a，y_a，z_a}为绝对坐标系；CS_g={O_g；x_g，y_g，z_g}与齿轮固联，z_g轴与齿轮轴线相重；CS_w={O_w；x_w，y_w，z_w}与砂轮固联，z_w轴与砂轮轴线相重。另外建立CS_e、CS_d两个辅助坐标系。图中，K₁、K₂为机床常数，当机床校准安装后这2个值就确定了，C_x、C_y、C_z、ψ_a、ψ_c分别为轴X、Y、Z、A、C的运动参数。

设在绝对坐标系CS_a内任一点的径向矢量为r^(a)，同一点在砂轮坐标系CS_w内的径向矢量为r^(w)，则有

$ {\mathit{\boldsymbol{r}}^{\left( {\rm{w}} \right)}} = {\mathit{\boldsymbol{M}}_{{\rm{wa}}}}{\mathit{\boldsymbol{r}}^{\left( {\rm{a}} \right)}} = {\mathit{\boldsymbol{M}}_{{\rm{wd}}}}{\mathit{\boldsymbol{M}}_{{\rm{de}}}}{\mathit{\boldsymbol{M}}_{{\rm{eg}}}}{\mathit{\boldsymbol{M}}_{{\rm{ga}}}}{\mathit{\boldsymbol{r}}^{\left( {\rm{a}} \right)}}。$

(13)

式中，${\mathit{\boldsymbol{M}}_{{\rm{wd}}}}=\left[ {\begin{array}{*{20}{c}} 1&0&0&0\\ 0&1&0&{ - {C_y}}\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right] $,

$ {\mathit{\boldsymbol{M}}_{{\rm{de}}}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0\\ 0&{\cos {\psi _{\rm{a}}}}&{ - \sin {\psi _{\rm{a}}}}&{{K_2}\sin {\psi _{\rm{a}}}}\\ 0&{\sin {\psi _{\rm{a}}}}&{\cos {\psi _{\rm{a}}}}&{ - {K_2}\cos {\psi _{\rm{a}}}}\\ 0&0&0&1 \end{array}} \right], $

$ {\mathit{\boldsymbol{M}}_{{\rm{eg}}}} = \left[ {\begin{array}{*{20}{c}} 1&0&0&{ - {C_x}}\\ 0&1&0&{{K_1}}\\ 0&0&1&{ - {C_z}}\\ 0&0&0&1 \end{array}} \right], $

$ {\mathit{\boldsymbol{M}}_{{\rm{ga}}}} = \left[ {\begin{array}{*{20}{c}} {\cos {\psi _c}}&{ - \sin {\psi _c}}&0&0\\ {\sin {\psi _c}}&{\cos {\psi _c}}&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right]。$

由式(13)可得

$ {\mathit{\boldsymbol{M}}_{{\rm{wa}}}} = \left[ {\begin{array}{*{20}{c}} {\cos {\psi _c}}&{ - \sin {\psi _c}}&0&{ - {C_x}}\\ {\cos {\psi _{\rm{a}}}\sin {\psi _c}}&{\cos {\psi _{\rm{a}}}\cos {\psi _c}}&{ - \sin {\psi _{\rm{a}}}}&{{E_1}}\\ {\sin {\psi _{\rm{a}}}\sin {\psi _c}}&{\sin {\psi _{\rm{a}}}\cos {\psi _c}}&{\cos {\psi _{\rm{a}}}}&{{F_1}}\\ 0&0&0&1 \end{array}} \right], $

(14)

式中，$\left\{ \begin{array}{l} {E_1} = {K_1}\cos {\psi _{\rm{a}}} + {K_2}\sin {\psi _{\rm{a}}} + {C_z}\sin {\psi _{\rm{a}}} - {C_y},\\ {F_1} = {K_1}\sin {\psi _{\rm{a}}} - {K_2}\cos {\psi _{\rm{a}}} - {C_z}\cos {\psi _{\rm{a}}}。\end{array} \right. $

坐标系CS_a向CS_w的变换矩阵，可以利用上述各矩阵的逆矩阵求得

$ \begin{array}{l} {\mathit{\boldsymbol{r}}^{\left( {\rm{a}} \right)}} = {\mathit{\boldsymbol{M}}_{{\rm{aw}}}}{\mathit{\boldsymbol{r}}^{\left( {\rm{w}} \right)}} = \mathit{\boldsymbol{M}}_{{\rm{aw}}}^{ - 1}{\mathit{\boldsymbol{r}}_{\rm{w}}} = \\ \;\;\;\;\;\;\;\mathit{\boldsymbol{M}}_{{\rm{ga}}}^{ - 1}\mathit{\boldsymbol{M}}_{{\rm{ge}}}^{ - 1}\mathit{\boldsymbol{M}}_{{\rm{de}}}^{ - 1}\mathit{\boldsymbol{M}}_{{\rm{wd}}}^{ - 1}{\mathit{\boldsymbol{r}}^{\left( {\rm{w}} \right)}}。\end{array} $

(15)

由式(13)、(15)可得：

$ {\mathit{\boldsymbol{M}}_{{\rm{aw}}}} = \left[ {\begin{array}{*{20}{c}} {\cos {\psi _c}}&{\cos {\psi _{\rm{a}}}\sin {\psi _c}}&{\sin {\psi _{\rm{a}}}\sin {\psi _c}}&{{D_2}}\\ { - \sin {\psi _c}}&{\cos {\psi _{\rm{a}}}\cos {\psi _c}}&{\sin {\psi _{\rm{a}}}\cos {\psi _c}}&{{E_2}}\\ 0&{ - \sin {\psi _{\rm{a}}}}&{\cos {\psi _{\rm{a}}}}&{{F_2}}\\ 0&0&0&1 \end{array}} \right], $

(16)

$ \left\{ \begin{array}{l} {D_2} = \left( {{C_y} - {K_1} - {K_2}\sin {\psi _{\rm{a}}}} \right)\sin {\psi _c} + {C_x}\cos {\psi _c},\\ {E_2} = \left( {{C_y} - {K_1} - {K_2}\sin {\psi _{\rm{a}}}} \right)\cos {\psi _c} - {C_x}\sin {\psi _c},\\ {F_2} = {K_2}\cos {\psi _{\rm{a}}} + {C_z}。\end{array} \right. $

3.2 虚拟球心速度及特征点的坐标变换

前面给出了惯性坐标架中参考点线性进给速度及砂轮轴角速度计算方法。图 6所示的五轴磨齿机典型数控加工代码为：N20 G01 X100 Y-1.5 Z10.5 A13 C-10 F100 M03 S3000，该命令行表示砂轮参考点从当前位置线性移动到点(100，-1.5，10.5)，A轴转到13°位置，C轴转到-10°位置，进给速度为100 mm/min，砂轮转速为3 000 r/min。

在图 6所示磨齿机的3个线性轴中，Y轴一般情况下不在水平位置，X、Y、Z 3个轴不能构成笛卡尔坐标系，数控代码还需变换到惯性坐标架中。因B轴不参数与坐标联动，仅需考虑Y轴的NC代码变换，即将Y轴的运动分解到CS_a坐标系的y_a、z_a方向，再进行速度计算，则式(11)中各轴的速度分量应表达为

$ \begin{array}{*{20}{c}} {\left\{ \begin{array}{l} \left( {{v_{0x}}} \right)_i^{\left( {\rm{a}} \right)} = \frac{{{{\left( {{x_t}} \right)}_{i + 1}} - {{\left( {{x_t}} \right)}_i}}}{{\Delta t}},\\ \left( {{v_{0y}}} \right)_i^{\left( {\rm{a}} \right)} = \frac{{{{\left( {{y_t}} \right)}_{i + 1}} - {{\left( {{y_t}} \right)}_i}}}{{\Delta t}}\cos \left( {{A_i}} \right),\\ \left( {{v_{0z}}} \right)_i^{\left( {\rm{a}} \right)} = \frac{{{{\left( {{z_t}} \right)}_{i + 1}} - {{\left( {{z_t}} \right)}_i}}}{{\Delta t}} + \frac{{{{\left( {{y_t}} \right)}_{i + 1}} - {{\left( {{y_t}} \right)}_i}}}{{\Delta t}}\sin \left( {{A_i}} \right), \end{array} \right.}\\ {\left( {i = 1,2, \cdots ,N - 1} \right)。} \end{array} $

(17)

将式(12)、(17)代入式(10)中，可得到虚拟球心的空间速度v_q^(a)。再将其变换到活动标架CS_w中，得到虚拟球心速度v_q^(w)为

$ \mathit{\boldsymbol{v}}_q^{\left( {\rm{w}} \right)} = {\mathit{\boldsymbol{M}}_{{\rm{wa}}}}\mathit{\boldsymbol{v}}_q^{\left( {\rm{a}} \right)}。$

(18)

联立式(5)、(9)、(18)即可求得特征点C在活动坐标架中的径向矢量r_c^(w)，再变换到惯性坐标架中，即得其在惯性标架中的径向矢量r_c^(a)，

$ \mathit{\boldsymbol{r}}_c^{\left( {\rm{a}} \right)} = {\mathit{\boldsymbol{M}}_{{\rm{aw}}}}\mathit{\boldsymbol{r}}_c^{\left( {\rm{w}} \right)}。$

(19)

4 计算实例与分析 4.1 双参数点矢量族包络法的计算步骤

双参数点矢量族包络法主要有如下5个计算步骤。

1) 根据计算精度要求对砂轮母线进行点矢量离散，并求取点矢量对应的虚拟球参数；

2) 由式(10)、(12)、(17)、(18)求虚拟球心速度；

3) 由式(5)、(19)求得特征点在惯性坐标架中的坐标值；

4) 按上述方法求得某一时刻砂轮母线上所有点矢量对应的特征点，形成特征线；

5) 将不同时刻形成的特征线进行组合，即形成砂轮扫掠体包络面。

4.2 计算实例

以某一拓扑修形齿轮的五轴成形磨削为例，齿轮及磨削工艺参数具体见表 1所示。

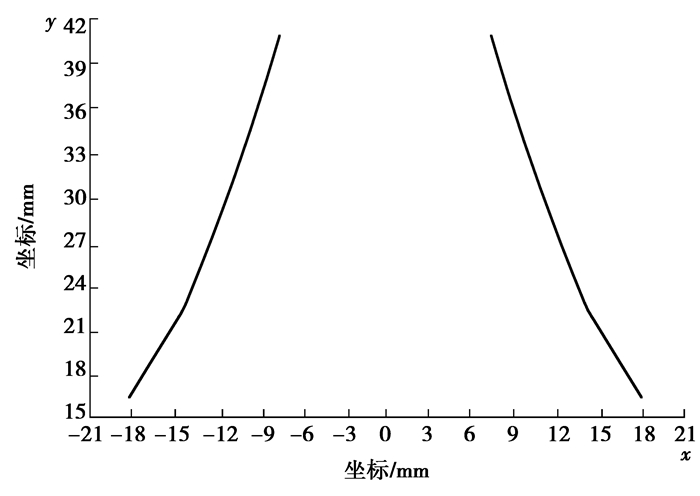
采用盘形砂轮进行双面磨齿。在实际磨齿工艺中，为减小磨削力，齿轮齿顶及其倒角、齿根圆一般由磨削前道工序——滚齿工艺保证，磨削工艺主要完成渐开线齿形部分精加工，故文中仅计算与齿轮渐开线部分对应的砂轮母线的包络情况。本例中产生有效包络面的砂轮母线如图 8所示。

按西门子840D数控系统格式编写的NC代码为

DEF INT SpindleNr

SpindleNr=﹩MA_SPIND_ASSIGN_TO_MACHAX[B]

M[SpindleNr]=3 S[SpindleNr]=3000

SpindleNr=﹩MA_SPIND_ASSIGN_TO_MACHAX[C]

M[SpindleNr]=70

G90G0 X0 Y468.3359 Z0 A13 C0

G01 X0.005 Y468.3363 Z0.0180 A13.0002 C0.0005 F100

X0.002 Y468.3361 Z0.0360 A-13.0001 C0.0011 F100

X0.003 Y468.3358 Z0.0540 A13.0003 C0.0016 F100

……

X-0.001 Y468.3357 Z42.9480 A12.9997 C1.2964 F100

X0.002 Y468.3361 Z42.9660 A12.9999 C1.2969 F100

X0.001 Y468.3358 Z42.9840 A13.0001 C1.2974 F100

End

在Matlab中编制程序进行包络面计算。由于砂轮磨齿时在砂轮轴线两侧产生包络面，其中一侧包络面形成齿面的磨削部分，另一侧不参与齿轮磨削，为辅助包络面。文中选取6个位置处的特征线为计算对象(未计算辅助包络特征线)，并将特征线与修形螺旋曲面进行比较，特征线基本与修形螺旋曲面吻合，验证了文中方法的正确性，如图 9所示。

4.3 结果分析与讨论

1) 双参数点矢量族包络法中，点矢量对应的虚拟球参数能用于后续的精度评估，几何特性直观。

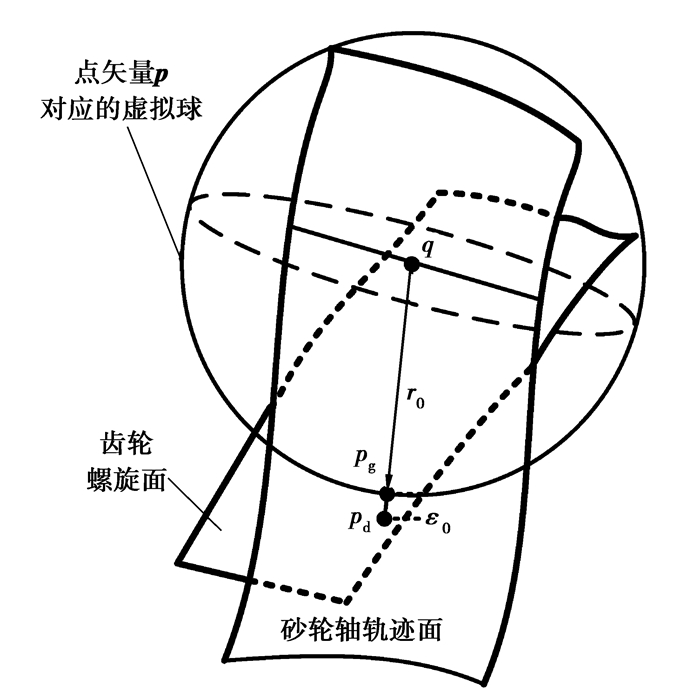
如图 10所示，某一时刻母线点矢量p对应的虚拟球参数为球心q、球半径r₀，特征点p_g处法向矢量为qp_g，从球心沿法线方向作一直线与齿轮螺旋面相交于p_d，则得磨削误差为ε₀=‖qp_d‖-r₀。

2) 由于直线、圆弧具有非常规则的解析表达形式，其上点矢量的虚拟球参数易于计算，有助于控制特征点的计算密度，从而降低计算复杂性。为此，可先计算砂轮母线上各分段点处对应的特征点，这些特征点将特征线分为多段，每段与母线中的直线或圆弧一一对应。

3) 包络面由各刀位下的特征线形成，而特征线为组合曲线，其中的每段曲线都可形成包络面，则砂轮扫掠体包络面可看成多个包络面的组合。因此该方法可建立包络面的组合表达模型，有利于精度评估及路径优化中的分片计算。

4) 点矢量的方向直接决定虚拟球心位置，进而决定特征点位置。尖点处至少会有2个点矢量，也即至少对应2个特征点。因此，在对砂轮点进行拟合时，生成的母线各分段曲线在分段点处应连续，避免生成尖点。

5 结论

1) 文中提出的点矢量双参数运动法，具有直观的几何特性，采用虚拟球参数及虚拟球心速度进行特征点求解，适宜于复杂母线砂轮的包络面计算。

2) 给出了基于五轴磨削数控代码的虚拟球心速度计算方法，建立了五轴磨齿机砂轮包络面的解析计算模型。

3) 文中研究成果可应用于齿轮磨削仿真中，并在螺旋曲面成形加工控制系统轨迹优化以及加工精度评估方面具有工程应用价值。