b. 重庆大学 软件学院, 重庆 400044
b. School of Software Engineering, Chongqing University, Chongqing 400044, China
针对未来几小时甚至一天到几天的电力负荷变化所做的预测即为电力系统短期负荷预测的主要研究内容。对电力系统进行正常的调度以及为发电厂、变电站制定合理的检修计划都需要依赖精确的短期负荷预测结果[1]。此外,电力系统短期负荷预测结果的优劣对选择合理的电网备用容量、制定经济高效的发电计划以及电网稳定运行都具有十分重要的影响[2]。由于负荷需求始终在动态变化,并受日类型、天气状况、温度、湿度、特别事件[3]等诸多随机因素的影响,因此寻找出诸多因素对电力负荷具体的作用,找寻一种适应能力较强的算法,成为了当前负荷预测工作的重中之重。
现有预测方法包括多元线性回归法[4]、随机时间序列法[5]、人工神经网络[6-10]、专家系统以及灰色系统理论[11-14]等。根据经验选择输入变量,无法体现出各输入变量对于输出值影响的重要程度,不能恰当地反映输入与输出之间的实际关系。神经网络由于具有优秀的自适应和自学习能力,被广泛应用于短期负荷预测工作中。在现有的短期负荷预测方法中,为了更好地提高负荷预测的精度,常常将负荷预测日类型及气象因素作为神经网络的输入量,但增加输入量必然使网络的收敛速度下降,并有可能导致算法陷入局部极值,如文献[6]中提出的基于反向传输(BP)神经网络的短期负荷预测算法,对样本容量需求较大,收敛速度较慢,且不能克服算法容易陷入局部极值的缺陷。文献[7]针对这一难题,将BP网络和混沌算法相结合,虽然解决了算法容易陷入局部极值的问题,但是预测的精度却不够理想。文献[8]提出了基于免疫BP网络算法,用以解决传感器阵列信号的模式识别,比较满意地克服了交叉敏感的问题,显著地提高了检测精度。
文中提出一种基于改进人工免疫算法和BP神经网络算法的电力系统短期负荷预测方法。该算法利用改进矢量距优化人工免疫算法,结合BP网络的优点,在人工免疫网络的设计中,融入了自适应变化策略的免疫调节原理,采用了新的个体编码方式、神经元适应度函数,并利用改进的免疫算法对样本进行学习,从而提高预测精度。
1 人工免疫算法人工免疫算法(Artificial immune algorithm,AIA)是一种模仿生物的免疫系统的启发式仿生智能算法[15-18]。在近些年的研究中,人工免疫算法被广泛应用于解决函数或者神经网络的优化问题。在优化过程中,该算法将待优化对象,即算法的约束条件和目标解作为抗原,将最优解作为抗体。通过人工免疫算法的抗体抗原结合力原理选择待优化对象的最优解。
人工免疫算法是对生物学中免疫系统的模拟,具有抗体多样性的优点,一旦有抗原进入,免疫系统将产生大量的抗体进行抵抗。人工免疫算法即是如此保持种群的多样性,并提高算法的全局搜索能力。通过对抗体进行抑制和促进,达到免疫系统的动态平衡,从而增强免疫算法的局部搜索能力,达到增强种群个体适应力的目的。
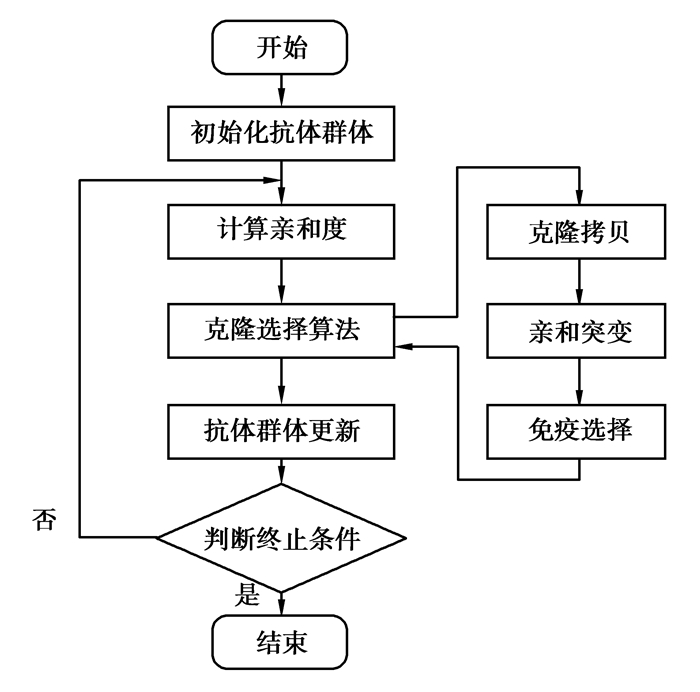
在采用人工免疫算法进行优化过程中,首先在种群中挑选亲和度较高的抗体进化,再进行克隆,使每个抗体均有相应的具有一定亲和度的克隆群,其中一部分用于进化,其他用于留作记忆细胞。然后根据和母体亲和度的差异,细胞的克隆个体按一定概率进行变异,在对细胞个体进行选择中,母体也将和克隆群体一起竞争,在整个竞争群体中选择存活的个体作为下一代种群的抗体母体。人工免疫算法即是如此不断循环迭代直至得到问题的最优解,其算法原理如图 1所示。
|
图 1 人工免疫算法的基本原理 |
具体待优化的问题决定了人工神经网络的输入量和输出量。在隐层节点中,神经元不仅需要包括输入、输出层的连接定义,而且需要包括其隐层节点的定义。径向基函数采用隐含层神经元函数
| $ \mathit{\Phi} = \left( {\left\| {X - {C_i}} \right\|,{\sigma _i}} \right) = \exp \left[ { - {{\left\| {X - {C_i}} \right\|}^2}/\left( {2\sigma _i^2} \right)} \right], $ | (1) |
人工免疫网络输出为
| $ Y = \sum\limits_{i = 1}^{{N_t}} {{\omega _i}} \exp \left[ { - {{\left\| {X - {C_i}} \right\|}^2}/\left( {2\sigma _i^2} \right)} \right], $ | (2) |
式中:X,Ci∈Rn,Nt代表神经网络中的隐层神经元个数;X为样本输入;‖·‖是欧几里德范数;ωi是第i个网络的输出节点和网络隐层节点相互间的权值(i=1,2,…,Nt);Ci,σi为第i个神经元的中心和宽度。
2.2 基于自适应策略的矢量距优化的免疫算法基于矢量距优化的免疫算法的基本原理,设免疫算法中抗体种群X={Bi}中包含n个B细胞,那么免疫算法中抗体适应度f(Bi)在种群X上的矢量距可由式(3)[19-20]表示:
| $ \rho \left( {{B_i}} \right) = \sum\limits_{j = 1}^n {\left| {f\left( {{B_i}} \right) - f\left( {{B_j}} \right)} \right|} 。$ | (3) |
式中,1/ρ(Bi)为抗体浓度,其抗体浓度的概率公式为
| $ \begin{align} {\rho _{\rm{s}}}\left( {{B_i}} \right) =& \frac{{\rho \left( {{B_i}} \right)}}{{\sum\limits_{i = 1}^n {\rho \left( {{B_i}} \right)} }} = \\ & \frac{{\sum\limits_{i = 1}^n {\left| {f\left( {{B_i}} \right) - f\left( {{B_j}} \right)} \right|} }}{{\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\left| {f\left( {{B_i}} \right) - f\left( {{B_j}} \right)} \right|} } }}。\end{align} $ | (4) |
由式(4)可知,矢量距优化的免疫算法不仅能够满足实数形式的网络优化,而且可以满足解的多样性要求。变异操作中的变异方式为
| $ B_i^{k + 1} = B_i^k + \alpha rand\left( \cdot \right), $ | (5) |
式中,α表示免疫算法中的变异尺度,它对算法的性能的优劣十分重要。选取较大的变异尺度值,利于算法收敛,但精度差;选取较小值时,利于算法的精度,但收敛性差。通过自适应策略优化,基于改进的变异尺度设计的抗体:
| $ \begin{align} B_i^{k + 1} = &B_i^k + \alpha _i^lrand\left( \cdot \right) = \\ &B_i^k + \frac{K}{{f\left( {B_i^k} \right)}}rand\left( \cdot \right), \end{align} $ | (6) |
式中:
而对于一个新的种群抗体,如果通过改进免疫算法变异得到的种群抗体Bik+1的适应度f(Bik+1)>f(Bik),则用Bik+1替换原种群抗体Bik,并改变αil,否则继续实行对原种群抗体Bik优化改进免疫算法的变异操作,αil由式(7)进行调整
| $ \alpha _i^l = \left\{ \begin{array}{l} \frac{{\alpha _i^l}}{2},f\left( {B_i^{k + 1}} \right) > f\left( {B_i^k} \right),\\ \alpha _i^l,f\left( {B_i^{k + 1}} \right) \le f\left( {B_i^k} \right)。\end{array} \right. $ | (7) |
BP神经网络凭借其网络结构简单,算法易于实现的优点在电力系统中得到了充分的发展。BP算法的收敛方向是当前网络函数值减小最快的方向,虽然BP网络算法属于梯度下降的算法,但由于非线性函数通常都十分复杂,算法的收敛路径不能直接指向函数的极小值点,算法的收敛路径通常均为“之”字形分布,需要迭代很多步才能寻找到极小值点,从而使其收敛速度显著降低,限制了其在电力系统中的应用。文献[7]提出了参数可调的改进的激励函数,使其收敛速度得到了明显改善。
三参数可调的激励函数
| $ {F_{a,b,\lambda }}\left( x \right) = \frac{1}{{1 + \exp \left( { - \frac{{x - b}}{\lambda }} \right)}} + a, $ | (8) |
式中:a为激励函数里的偏移参数,b为激励函数里面的阈值参数,λ为激励函数里面的陡度因子。函数Fa,b,λ(x)的非线性表达能力比F(x)更好,激励函数的垂直位置由偏移函数决定,水平位置由阈值参数决定。激励函数的形状由陡度因子决定。通过激励函数的调节,把传统的BP神经网络算法改进为利用激励函数调节的BP网络学习算法,使传统BP神经网络算法收敛速度慢及精度差的缺点得到了极大的改善。
3.2 基于改进免疫算法和激励函数可调的BP神经网络的电力短期负荷预测模型基于自适应策略改进的人工免疫算法和三参数可调的BP网络的电力系统短期负荷预测方法构造BP-AA算子,提高了短期负荷预测算法的全局搜索能力。并且利用BP-AA算子对种群中B细胞所对应网络中参数模板为零的参数进行修正,具有网络节点数目不改变的优点。
算法修正过程如下:通过输入样本计算B细胞涉及的各项性能指标,然后利用参数可调的激励函数算法算出各级梯度值,再对各级参数进行修正,利用规则将新的编码重排在原免疫网络的B细胞中,则得到了可调激励函数的算子。算法流程如下:
1) 首先将抗原载入进行种群初始化,进而生成种群的初始值;
2) 计算网络中B细胞的亲和度值,从而确定免疫网络中克隆后代的数目;
3) 克隆免疫网络中的B细胞,克隆后的种群1形成;
4) 对种群1进行参数变异,得到种群2;
5) 计算上述种群2中每个个体的亲和度;
6) 将种群2和种群1进行比较,判断种群2是否优于种群1,若判断为是,则替换种群1的参数编码,若判断为否,执行步骤7);
7) 分别针对种群中的每个细胞用参数可调的激励函数算子对其参数进行更新;
8) 逐次计算更新之后的每个种群个体的亲和度值;
9) 对亲和度进行判定,若优于其他个体,则执行步骤10),否则替换原细胞,执行步骤2);
10) 判定优化后的网络是否满足其收敛条件,若满足,则执行步骤11),若不满足其收敛条件,则删除其中亲和度比较低的细胞,然后产生新的细胞予以补足,执行步骤2);
11) 选择种群中亲和度数值最大的B细胞作为免疫网络的结果予以输出。
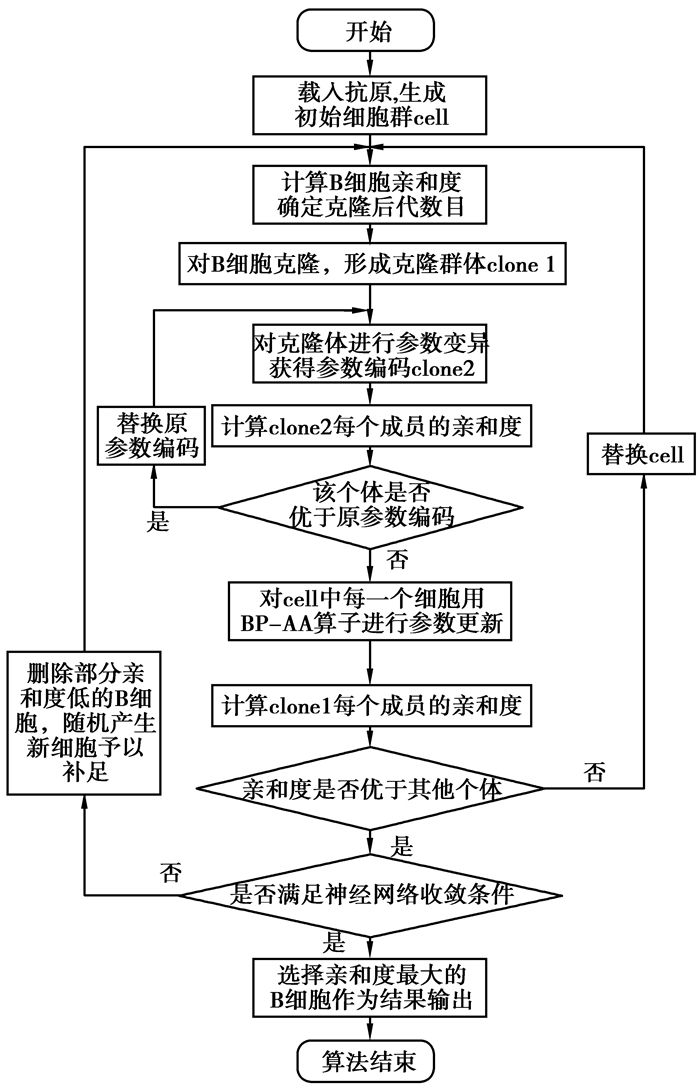
利用改进免疫算法和BP神经网络的预测流程图如图 2所示。
|
图 2 算法流程图 |
根据某供电局提供的2009年1月1日到2009年3月31日每天的电力负荷数据,分别采用文中提出的基于改进免疫算法优化的BP神经网络和文献[7]中提出的基于混沌方法的BP神经网络分别对其进行负荷预测,结果如表 1所示。
| 表 1 2种预测算法结果比较 |
从表 1数据可以得出,基于改进免疫算法优化的BP神经网络在预测精度上更胜一筹,其最大误差仅有3.72%,平均误差为1.58%,而基于混沌方法的BP神经网络最大误差达到了5.41%,平均误差也有1.84%,这说明文中所提出的电力系统短期负荷预测模型更好。
5 结论文中将改进免疫算法和BP神经网络相结合,利用改进免疫算法的全局寻优能力,解决了以往BP神经网络易于陷入局部极值的缺陷,并充分利用了BP神经网络局部寻优特点,通过融入自适应变化策略的免疫调节原理,采用新的个体编码方式达到了改进算法的效果。将其应用于电力系统短期负荷预测,不仅提高了算法的收敛速度,而且较好地提高了预测的精度,比传统的短期负荷预测方法更具实用价值。
| [1] |
魏少岩, 吴俊勇.
基于灰色模型和Kalman平滑器的多母线短期负荷预测[J]. 电工技术学报, 2010, 25(2): 158–162.
WEI Shaoyan, WU Junyong. Short-term bus load forecasting based on grey model and Kalman smoother[J]. Transactions of China Electrotechnical Society, 2010, 25(2): 158–162. (in Chinese) |
| [2] | Tomonobu S, Hitoshi T, Uezato K K, et al. One-hour-ahead load forecasting using neutral network[J]. IEEE Transactions on Power Systems, 2002, 17(1): 113–118. DOI:10.1109/59.982201 |
| [3] | Yang H T, Huang C M. Identification of ARMAX model for short-term load forecasting:an evolutionary programming approach[J]. IEEE Transactions on Power Systems, 1996, 11(1): 403–408. DOI:10.1109/59.486125 |
| [4] |
毛李帆, 江岳春, 龙瑞华, 等.
基于偏最小二乘回归分析的中长期电力负荷预测[J]. 电网技术, 2008, 32(19): 71–77.
MAO Lifan, JIANG Yuechun, LONG Ruihua, et al. Medium-and long-term load forecasting based on partial least squares regression analysis[J]. Power System Technology, 2008, 32(19): 71–77. (in Chinese) |
| [5] |
谭忠富, 张金良.
利用多因素小波变换和多变量时间序列模型的日前电价预测[J]. 中国电机工程学报, 2010, 30(1): 103–110.
TAN Zhongfu, ZHANG Jinliang. Day-ahead electricity price forecasting based on multi-factor wavelet analysis and multivariate time series models[J]. Proceedings of the CSEE, 2010, 30(1): 103–110. (in Chinese) |
| [6] |
姚李孝, 宋玲芳, 李庆宇, 等.
基于模糊聚类分析与BP网络的电力系统短期负荷预测[J]. 电网技术, 2005, 29(1): 20–23.
YAO Lixiao, SONG Lingfang, LI Qingyu, et al. Power system short-term load forecasting based on fuzzy clustering analysis and BP neural network[J]. Power System Technology, 2005, 29(1): 20–23. (in Chinese) |
| [7] |
张晓星, 程其云, 周湶, 等.
激励函数可调的混沌神经网络短路负荷预测[J]. 高电压技术, 2005, 31(7): 51–54.
ZHANG Xiaoxin, CHENG Qiyun, ZHOU Qua, et al. Short term load forecasting by using neural networks with variable activation functions and embedded chaos algorithm[J]. High Voltage Engineering, 2005, 31(7): 51–54. (in Chinese) |
| [8] |
陈伟根, 齐辉, 王有元, 等.
一种气体传感器阵列检测模式识别新方法[J]. 重庆大学学报, 2010, 33(1): 61–66.
CHEN Weigen, QI Hui, WANG Youyua, et al. A new pattern recognition method of gas sensor array detection[J]. Journal of Chongqing University, 2010, 33(1): 61–66. (in Chinese) |
| [9] | Papageorgiou M, Kotsialos A, Poulimenos A. Long-term sales forecasting using holt-winters and neutral network methods[J]. Journal of Forecasting, 2005, 24(5): 353–368. DOI:10.1002/(ISSN)1099-131X |
| [10] | Zhang B L, Dong Z Y. An adaptive neural-wavelet model for short term load forecasting[J]. Electric Power System Researeh, 2001, 59(2): 121–129. DOI:10.1016/S0378-7796(01)00138-9 |
| [11] | Akay D, Atak M. Grey predietion with rolling mechanism for electricity demand forecasting of Turkey[J]. Energy, 2007, 32(9): 1670–1675. DOI:10.1016/j.energy.2006.11.014 |
| [12] | Hsu C C, Chen C Y. Applications of improved grey predication model for power demand forecasting[J]. Energy Conversion and Management, 2003, 44(14): 2241–2249. DOI:10.1016/S0196-8904(02)00248-0 |
| [13] | Yao A W L, Chi S C, Chen J H. An improved gre-based approach for electricity demand forcasting[J]. Electric Power Systems Researeh, 2003, 67(3): 217–224. DOI:10.1016/S0378-7796(03)00112-3 |
| [14] | Lin Y H, Lee P C. Novel high-precision grey forecasting model[J]. Automation in Construction, 2007, 16(6): 771–777. DOI:10.1016/j.autcon.2007.02.004 |
| [15] |
尤勇, 盛万兴, 王孙安.
基于人工免疫网络的短期负荷预测模型[J]. 中国电机工程学报, 2003, 23(3): 26–30.
YOU Yong, SHENG Wanxing, WANG Sunan. Short-term load forecasting using artificial immune network[J]. Proceedings of the CSEE, 2003, 23(3): 26–30. (in Chinese) |
| [16] | Alfuhaid A S, El-Sayed M A H, Mahmoud M S. Cascaded artificial neural networks for short-term load forecasting[J]. IEEE Transactions on Power Systems, 1997, 12(4): 1524–1529. DOI:10.1109/59.627852 |
| [17] |
李如琦, 褚金胜, 谢林峰, 等.
IAFSA-RBF神经网络在短期负荷预测中的应用[J]. 电力系统及其自动化学报, 2011, 23(2): 142–146.
LI Ruqi, CHU Jingsheng, XIE Linfeng, et al. Application of IAFSA-RBF neural network to short-term load forecasting[J]. Proceedings of the CSU-EPSA, 2011, 23(2): 142–146. (in Chinese) |
| [18] |
周湶, 孙才新, 张晓星, 等.
基于多种群免疫遗传算法的配电网网架规划[J]. 重庆大学学报:自然科学版, 2005, 28(4): 36–41.
ZHOU Quan, SUN Caixin, ZHANG Xiaoxin, et al. Distribution network structure planning based on multi-population immune genetic algorithm[J]. Journal of Chongqing University:Natural Science Edition, 2005, 28(4): 36–41. (in Chinese) |
| [19] |
荆献勇, 肖明清, 余文波, 等.
改进免疫算法在预测过程神经网络中的应用[J]. 系统工程与电子技术, 2010, 32(10): 2136–2140.
JING Xianyon, XIAO Mingqin, YU Wenbo, et al. Application of improved immune algorithm in forecast procedure neural network[J]. Systems Engineering and Electronics, 2010, 32(10): 2136–2140. DOI:10.3969/j.issn.1001-506X.2010.10.26 (in Chinese) |
| [20] | Dash P K, Satpathy H P, Liew A C C, et al. A real-time short-term load forecasting system using functional link network[J]. IEEE Transactions on Power Systems, 1997, 12(2): 675–680. DOI:10.1109/59.589648 |
 2013, Vol. 36
2013, Vol. 36



