在电子对抗、跟踪遥测等工程应用领域,由于抛物面天线具有发射功率大、副瓣较低、结构简单易加工、相关技术较成熟等优点,常常被选做发射天线或者阵列单元。旋转抛物面天线是抛物面天线的一种,因其具有高增益、高效率、低噪声、宽频带等特性[1],被广泛应用于通信、雷达和电文等系统。
旋转抛物面天线通常以喇叭天线作为其馈源。由于喇叭天线的辐射场不是理想的球面波,因此不存在严格的相位中心[2],但工程上仍然需要确定一个近似的相位中心,并使其与抛物面焦点重合,以便得到最大的天线增益。确定喇叭天线近似相位中心有2种方法,一种是从理论近似分析求得[3],但计算公式很复杂,不能直接用于工程;另一种是实验方法,该方法将喇叭天线放置在抛物面天线的焦点附近做轴向移动,测取抛物面天线的增益最大(或主瓣宽度最窄)时的喇叭天线位置,从而确定出近似相位中心。实验方法虽然简单,但需对每一个频点进行重复实验,效率低、工作量大。因此,通过建立基于有限积分法的旋转抛物面天线的数值仿真模型,快速、有效地计算出旋转抛物面天线喇叭馈源相位中心位置。
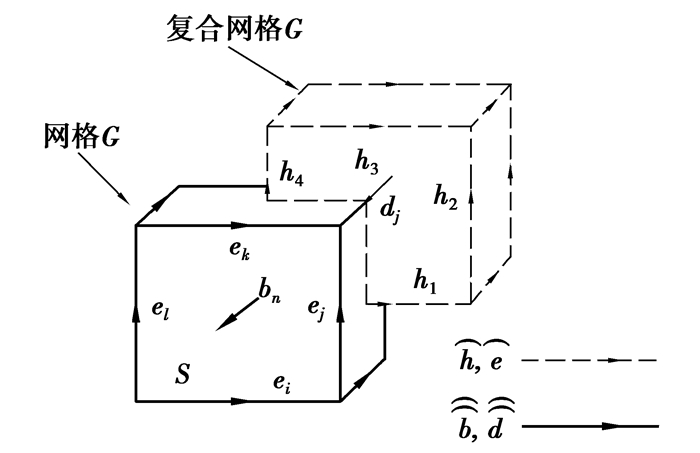
1 有限积分法原理(FIT)有限积分技术(finite integration technique)建立在对麦克斯韦积分方程组离散处理的基础上[4]。首先将计算空间划分成图 1所示的网格G和复合网格
|
图 1 空间离散网格和场量分布 |
对于法拉第电磁感应定律[4]
| $ \oint\limits_l {\mathit{\boldsymbol{E}}\left( {\mathit{\boldsymbol{r}},t} \right) \cdot {\rm{d}}\mathit{\boldsymbol{l}}} = - \iiint\limits_S {\frac{\partial }{{\partial t}}\mathit{\boldsymbol{B}}\left( {\mathit{\boldsymbol{r}},t} \right) \cdot {\rm{d}}\mathit{\boldsymbol{S}}}, $ | (1) |
其中l表示S面上4条棱边组成的闭合环路,ei、ej、ek和el为相邻2网格点间的电压,可以得到
| $ {e_i} + {e_j} - {e_k} - {e_l} = - \frac{{\rm{d}}}{{{\rm{d}}t}}{b_{\rm{n}}}。$ | (2) |
同理可得麦克斯韦积分方程组的其他3个方程的离散形式。如果在每一个网格的各个面上都写出这样的方程,可得矩阵方程组
| $ \mathit{\boldsymbol{C\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e} }} = - \frac{{\rm{d}}}{{{\rm{d}}t}}\mathit{\boldsymbol{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{b} } }}, $ | (3) |
| $ \mathit{\boldsymbol{\tilde C\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }} = - \frac{{\rm{d}}}{{{\rm{d}}t}}\mathit{\boldsymbol{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} } }} + \mathit{\boldsymbol{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{j} } }}, $ | (4) |
| $ \mathit{\boldsymbol{S\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{b} } }} = 0, $ | (5) |
| $ \mathit{\boldsymbol{\tilde S\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} } }} = q, $ | (6) |
式中,C(
电(磁)压和电(磁)通量通过材料性能矩阵Mε、Mμ和Mσ联系起来
| $ \mathit{\boldsymbol{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} } }} = {\mathit{\boldsymbol{M}}_\varepsilon }\mathit{\boldsymbol{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e} }},\mathit{\boldsymbol{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{b} } }} = {\mathit{\boldsymbol{M}}_\mu }\mathit{\boldsymbol{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{h} }},\mathit{\boldsymbol{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{j} } }} = {M_\sigma }\mathit{\boldsymbol{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{e} }}。$ | (7) |
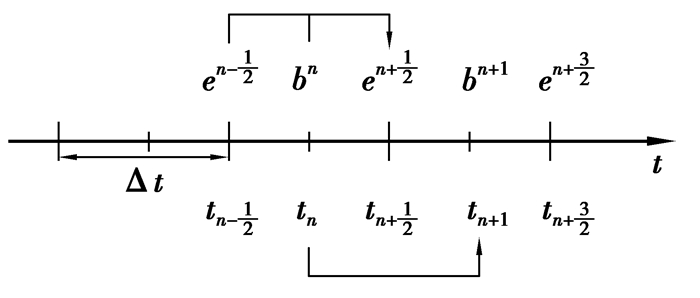
在时域内解算网格方程,运用蛙跳算法对时间轴进行离散,如图 2所示。
|
图 2 蛙跳算法图示 |
在蛙跳算法中,电场磁场在时间顺序上交替抽样,抽样时间间隔彼此相差半个时间步,网格迭代方程如下
| $ {e^{{\rm{n}} + 1/2}} = {e^{{\rm{n}} - 1/2}} + \Delta t\mathit{\boldsymbol{M}}_\varepsilon ^{ - 1}\left[ {\tilde C\mathit{\boldsymbol{M}}_\mu ^{ - 1}{b^n} + j_{\rm{s}}^n} \right], $ | (8) |
| $ {b^{n + 1}} = {b^n} - \Delta t\mathit{\boldsymbol{C}}{e^{{\rm{n}} + 1/2}}, $ | (9) |
式中,n代表时间步数,Δt是时间步长,满足以下条件就能保证迭代稳定
| $ \Delta t \le {\left( {c\sqrt {\frac{1}{{\Delta {x^2}}} + \frac{1}{{\Delta {y^2}}} + \frac{1}{{\Delta {z^2}}}} } \right)^{ - 1}}。$ | (10) |
FIT法的优势是不需要矩阵求逆,这样可计算的区域就比较大,另外结合网格局部加密技术,可以确保馈源的精确仿真得以快速的进行。
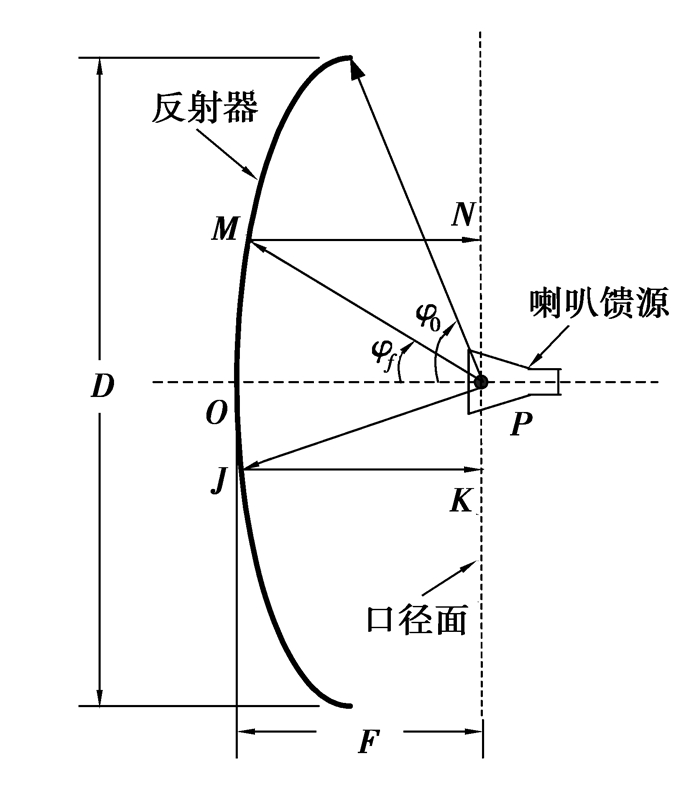
2 旋转抛物面天线工作原理旋转抛物面天线主要由2部分组成:一个旋转抛物面结构的反射器和一个非常小的馈电天线即馈源,如图 3所示。图中,D为反射器的口径尺寸,F为其焦距,OP为其轴线,φf是焦点与反射器上任意点连线与轴线OP的夹角,φ0为反射器口径对焦点的半张角。
|
图 3 旋转抛物面天线原理简图 |
旋转抛物面天线具有以下2个重要性质:
1) 由焦点P发出的射线,经反射器反射后,反射线相互平行且均平行于其轴线OP。反过来平行于OP的射线,经反射器的反射作用,其反射线均汇聚于焦点P处。
2) 由焦点P发出的射线,经反射器反射到达口径面时,其长度相等,即PM+MN=PJ+JK,并且等于2F。
因此,当把馈源置于焦点位置并使馈源的相位中心与反射器焦点重合,则馈源辐射出的球面波经反射器反射后,在口面上将转变成平面波,使反射器口面场形成均匀分布。均匀口面场将产生强方向性辐射场,这就是旋转抛物面天线产生强方向性辐射场的原理。反之,如果把旋转抛物面天线用作接收天线,入射波又是平面波形式,经反射器反射后,则会把平面波转换成球面波传送到位于焦点位置的馈源,形成聚集接收,增加其接收信号的强度。
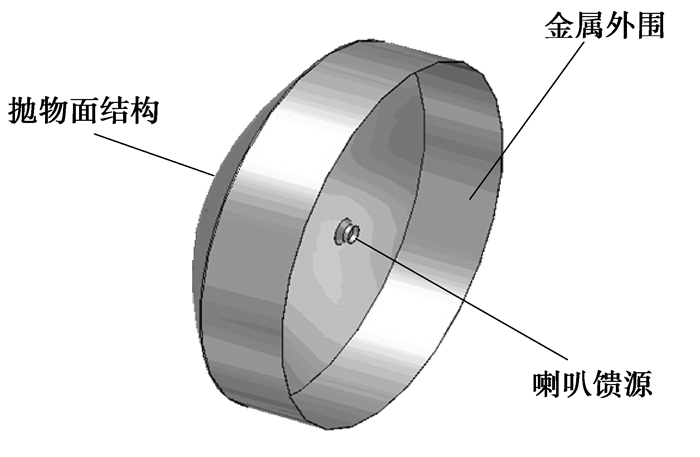
3 旋转抛物面天线仿真模型 3.1 旋转抛物面天线模型以某一旋转抛物面天线为原型,建立用于电磁仿真的旋转抛物面天线模型如图 4所示,为进行电磁仿真,对模型进行了必要的简化。抛物面结构与其边缘附加的金属外围呈无缝连接,忽略喇叭馈源支撑杆和波导的影响,整个天线的材料设为良导体,计算区域均为真空。简化后的模型既保留了原天线的特征,又减少了对计算机内存的需求,对计算结果的精确度影响不大。
|
图 4 旋转抛物面天线三维电磁仿真实体模型 |
笔者建立的天线仿真模型工作频率范围在4~5 GHz,为满足宽频电磁辐射求,选择高斯脉冲作为喇叭馈源的激励源,其时域形式[5]
| $ G\left( t \right) = \exp \left( { - \frac{{4{\rm{ \mathsf{ π} }}{{\left( {t - {t_0}} \right)}^2}}}{{{\tau ^2}}}} \right), $ | (11) |
其中,t0为高斯脉冲达最大值的时间,τ为脉冲宽度。为了保证高斯脉冲在t=0时近似为零,需有(2
对式(11)作傅里叶变换可得高斯脉冲的频域形式,即
| $ G\left( f \right) = \exp \left( { - {\rm{ \mathsf{ π} }}{\tau ^2}{f^2}/4} \right)。$ | (12) |
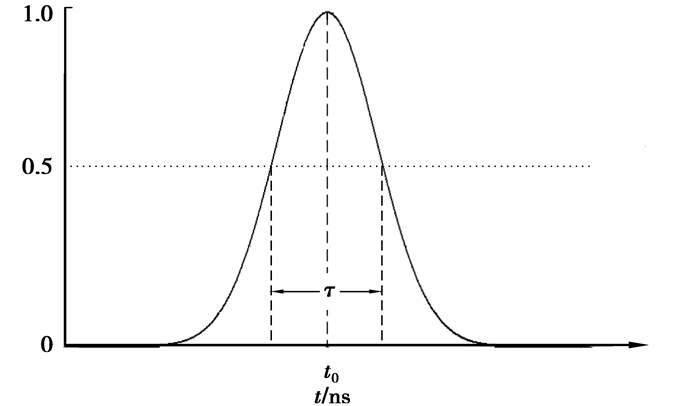
对于通信天线,脉宽τ取从上升沿50%幅值开始计算,直到脉冲下降到50%幅值时的持续时间[6],而下降沿50%幅值处的频率定为高斯脉冲的最高频率fmax。因此取fmax=5 GHz,根据式(12)得τ=0.187 9 ns。高斯脉冲时域形式如图 5所示,该脉冲覆盖了仿真天线的使用频率范围,可用于仿真模型计算。
|
图 5 高斯脉冲时域波形 |
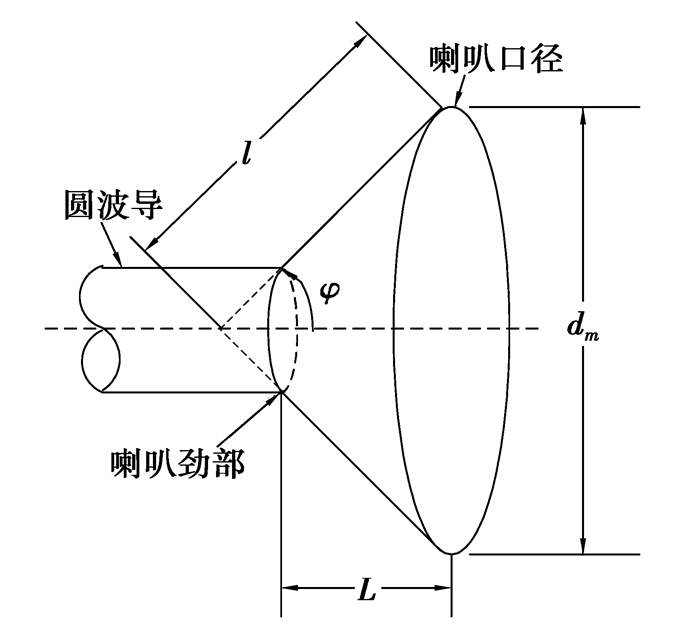
选择圆锥喇叭天线作为旋转抛物面天线的馈源,如图 6所示。
|
图 6 圆锥喇叭馈源模型 |
图 6中,dm是圆锥底直径,l是圆锥喇叭臂长,L是喇叭馈源颈部(圆锥与波导连接处)到口径的垂直距离,φ是馈源的照射半张角,与φ0近似相等。
对于一个实际的馈源,如要获得高口径效率,除需要满足其相位中心与抛物面焦点重合之外,它还应具有如下特点[7]:
1) 馈源的方向图应该是旋转对称的或平衡的;
2) 馈源方向图应该使抛物面的边缘照射EI(edge irradiate)约为-11 dB,此时馈源与反射器达到匹配状态;
3) 为避免遮挡辐射场,馈源的几何尺寸应较小,通常它的直径dm在一个波长的量级上。
为满足馈源方向图旋转对称的条件,选择通用的平衡馈源模型,其旋转对称方向图为[7]
| $ {F_f}\left( {{\varphi _f}} \right) = \left\{ \begin{array}{l} {\cos ^q}{\varphi _f}, - {\varphi _0} \le {\varphi _f} \le {\varphi _0};\\ 0, - {\varphi _0} > {\varphi _f} > {\varphi _0}。\end{array} \right. $ | (13) |
式中,q是以次方形式存在的无量纲实数,它的大小由边缘照射EI、反射器焦距F和口径D决定,其值可由式(14)计算得到。
| $ q = \frac{{\lg \left[ {EI \cdot \left( {1 + \frac{1}{{16{{\left( {\frac{F}{D}} \right)}^2}}}} \right)} \right]}}{{\lg \left[ {\cos \left( {2{{\tan }^{ - 1}}\frac{1}{{4\left( {\frac{F}{D}} \right)}}} \right)} \right]}}。$ | (14) |
为了使天线获得尽可能大的增益,馈源的方向图应该与反射器相匹配,即满足边缘照射约为EI=0.28(=-11 dB)。于是根据式(14)将q值求出后,可以利用式(15)验证边缘照射值是否满足要求[7]。
| $ EI = 20\lg \left( {{{\cos }^q}{\varphi _0}} \right) + 20\lg \left[ {\frac{{\left( {1 + \cos {\varphi _0}} \right)}}{2}} \right], $ | (15) |
式中,φ0与反射器的焦距、直径存在以下关系
| $ \frac{F}{D} = \frac{1}{4}{\rm{ctg}}\frac{{{\varphi _0}}}{2}。$ | (16) |
喇叭馈源直径dm由下式计算[2]
| $ {d_{\rm{m}}} = \sqrt {3\lambda l} , $ | (17) |
根据dm和l的三角函数关系式,在φ(≈φ0)已知的情况下,可以求得dm。
4 馈源相位中心位置的计算喇叭馈源的近似相位中心与抛物面反射器焦点重合时,抛物面天线的增益G(Gain)最大。通常喇叭馈源的相位中心偏离喇叭口径位于喇叭内,其位置取决于喇叭的尺寸,尤其是取决于它的张角。对于大张角的喇叭馈源,相位中心靠近喇叭颈部。减小张角,相位中心将向喇叭口径面移动,当张角减小到0时,相位中心便移至喇叭口径中心位置,此时口径面为等相位面。
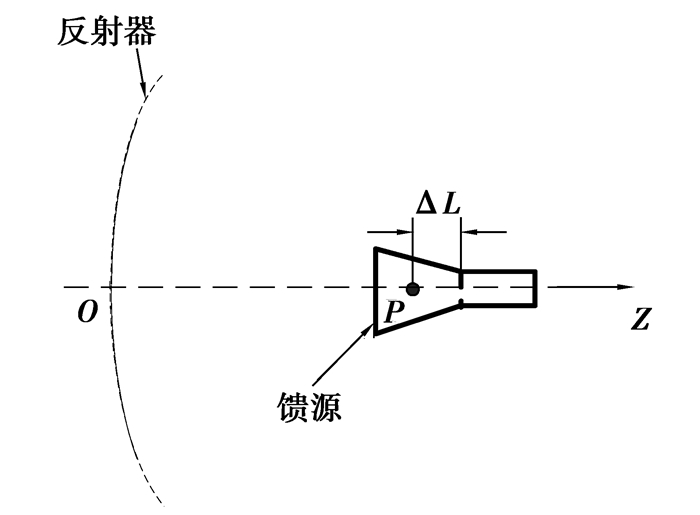
图 7给出了确定喇叭馈源相位中心位置与反射器焦点位置之间的关系。图中ΔL是喇叭颈部中心到反射器焦点P的距离。(当增益最大时,ΔL亦是喇叭颈部中心到馈源近似相位中心的距离)。取馈源的L为20 mm,则ΔL的取值范围为0~20 mm。
|
图 7 喇叭馈源相位中心位置仿真 |
天线增益G计算公式为[7]
| $ G = \frac{{4{\rm{ \mathsf{ π} }}}}{{{\lambda ^2}}}{\varepsilon _{{\rm{ap}}}}{A_p}, $ | (18) |
式中εap是反射器的口径效率,Ap是反射器的物理口径面积,天线模型D=1 500 mm,F=441 mm。
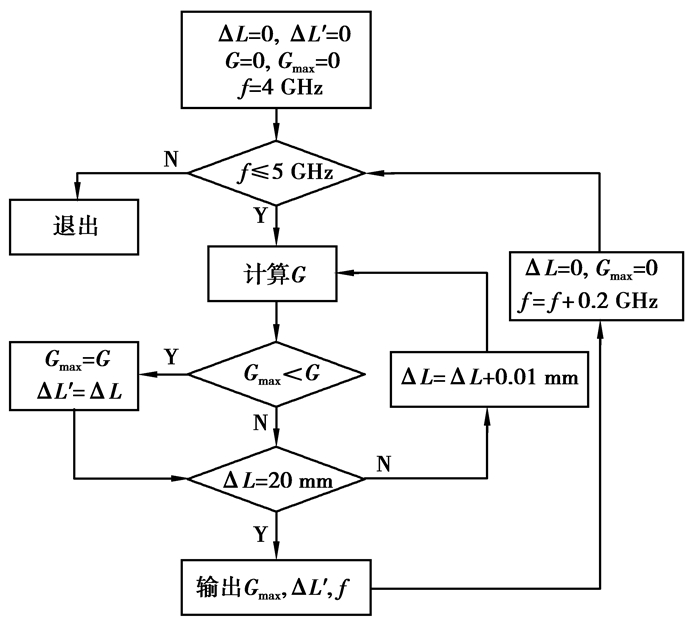
仿真时首先将喇叭颈部中心点置于焦点P上,即ΔL=0,然后沿z轴正向逐步移动喇叭馈源,直到喇叭口径面的中心与反射器的焦点重合,此时ΔL=20 mm。仿真过程中在4~5 GHz范围内每隔0.2 GHz取1个监测频点,共取6个频点进行研究,具体算法如图 8所示。表 1为6个频点近似相位中心的位置及对应增益。
|
图 8 馈源相位中心位置计算流程图 |
| 表 1 馈源近似相位中心的位置及对应增益 |
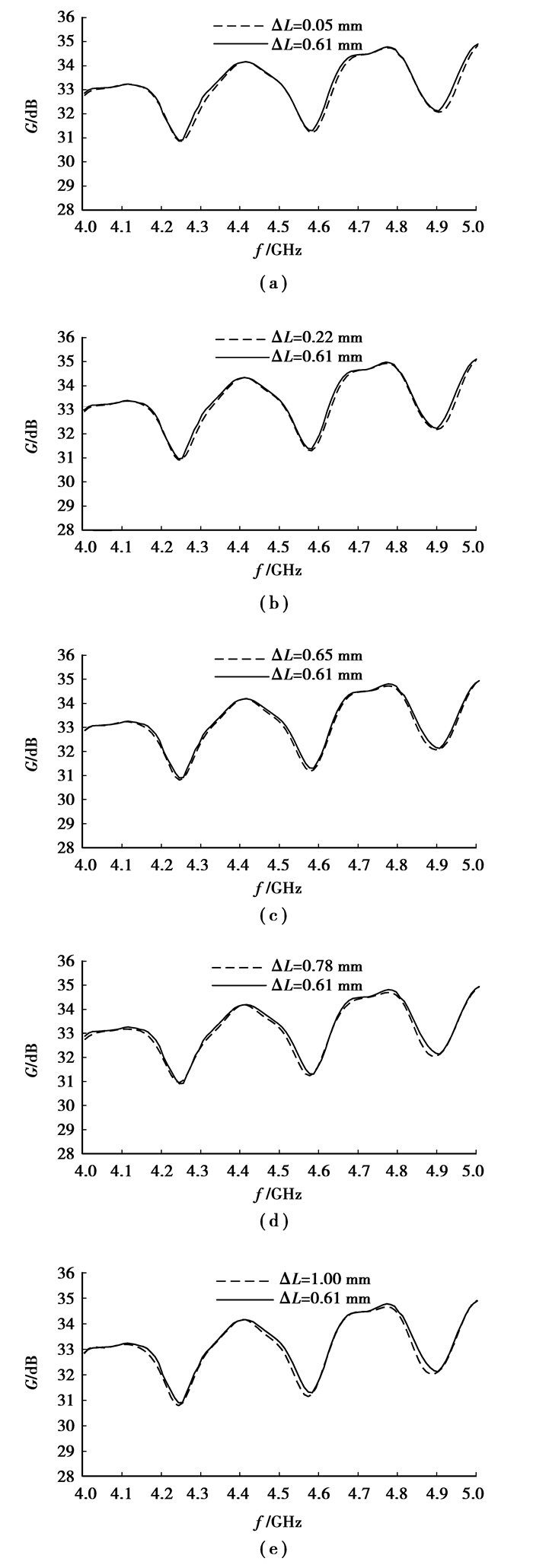
表 1中,针对给定的喇叭馈源每个频点,有一个近似相位中心与之对应,然而一个真实的抛物面天线电磁辐射频率在一个范围内,因此在4~5 GHz整个频段,ΔL的6个数值哪一个使旋转抛物面天线增益最大,还需要对每一个ΔL值进行全频段仿真,最后挑选出该抛物面天线馈源相位中心的最佳位置。在进一步仿真中,频率步长取0.01 GHz,最后得到馈源相位中心的最佳位置是ΔL=0.61 mm,仿真结果如图 9(a)~(e)所示。
|
图 9 ΔL= 0.61 mm与其他值的对比曲线 |
从图 9(a)~(e)可以看出馈源6个近似相位中心的增益曲线差别非常小,但ΔL=0.61 mm时的增益在4~5 GHz整个频段相对最佳。因此,在抛物面天线仿真模型中馈源的近似相位中心取在ΔL=0.61 mm处。
5 结语利用电磁场数值方法,确定了在4~5 GHz频率范围内,旋转抛物面天线馈源的最佳近似相位中心,省去了解析公式的繁琐计算和实验测量的大量重复性工作。建模方法和仿真研究过程可以运用到不同类型旋转抛物面天线的研究中去,从而为旋转抛物面天线馈源位置的确定提供有益的指导。
| [1] | 刘学观, 郭辉萍. 微波技术与天线[M]. 2版. 西安: 西安电子科技大学出版社, 2006. |
| [2] | Balanis C A. Antenna theory:analysis and design[M]. 3rd ed. New Jersey: John Wiley & Sons, Inc, 2005. |
| [3] | Kildal P.S.. Combined E- and H-plane phase centers of antenna feeds[J]. IEEE Transactions on Antennas and Propagation, 1983, 31(1): 199–202. DOI:10.1109/TAP.1983.1143009 |
| [4] | 祝言菊. 车载天线优化设计及对车内电磁环境影响研究[D]. 重庆: 重庆大学硕士学位论文, 2009. http://cdmd.cnki.com.cn/article/cdmd-10611-2009220583.htm |
| [5] | Kono N, Mizota H. Analysis of characteristics of grating lobes generated with Gaussian pulse excitation by ultrasonic 2-D array transducer[J]. NDT & E International, 2011, 44(6): 477–483. |
| [6] | 李锦萍. 电子线路:提高版·模拟电路与脉冲数字电路[M]. 北京: 电子工业出版社, 2000. |
| [7] | Stutzman W L, Thiele G A. 天线理论与设计[M]. 朱守正, 安同一, 译. 2版. 北京: 人民邮电出版社, 2006. |
| [8] | Nian F, Wang W. New theoretical analysis method for the phase center in the Fresnel region of complex structure antennas[J]. Journal of Systems Engineering and Electronics, 2008, 19(5): 865–871. DOI:10.1016/S1004-4132(08)60165-6 |
| [9] | Ruddle A R. Electromagnetic modelling for EMC[C]//Proceedings of the IEEE 7th International Conference on Computation in Electromagnetics, April 7-10, 2008, Brighton, UK. Piscataway:IEEE Press, 2008:170-174. http://ieeexplore.ieee.org/document/4563409/ |
| [10] | Öchsner A, Murch G E, Lemos M J S D. Cellular and porous materials:thermal properties simulation and prediction[M]. New Jersey: John Wiley & Sons, 2008. |
| [11] |
刘剑, 赵军明, 刘林华.
单层元胞结构金属泡沫的透射特性[J]. 工程热物理学报, 2010, 31(12): 2101–2104.
LIU Jian, ZHAO Junming, LIU Linhua. Transmittance characteristics of metal foams with single layer cellular structure[J]. Journal of Engineering Thermophysics, 2010, 31(12): 2101–2104. (in Chinese) |
| [12] | 焦健, 石丹, 高攸纲. 高压开关柜房间三维电磁场仿真分析[G]//中国通信学会. 第21届全国电磁兼容学术会议论文集. 河南: 电波科学学报, 2011, 26(Sup): 173-177. http://cpfd.cnki.com.cn/Article/CPFDTOTAL-ZGTH201104001041.htm |
| [13] |
郑军.
基于计算机仿真平台的弹上天线研究与设计[J]. 战术导弹技术, 2007, 12(5): 93–96.
ZHENG Jun. A study and design of on-board antenna based on computer simulation platform[J]. Tactical Missile Technology, 2007, 12(5): 93–96. (in Chinese) |
| [14] |
吴珊, 吴利民, 单财良.
基于高斯脉冲的认知超宽带无线电波形设计[J]. 空军雷达学院学报, 2009, 23(4): 291–292, 296.
WU Shan, WU Limin, SHAN Cailiang. Design of gaussian pulse-based CUWB radio waveforms[J]. Journal of Air Force Radar Academy, 2009, 23(4): 291–292, 296. (in Chinese) |
| [15] | Pommerenke D J, Jobava R G, Heinrich R. Numerical simulation of partial discharge propagation in cable joints using the finite difference time domain method[J]. IEEE Electrical Insulation Magazine, 2008, 18(6): 6–11. |
| [16] | Denissov D, Kohler W, Tenbohlen S, et al. Simulation of UHF PD wave propagation in plug-in cable terminations[C]//Proceedings of the Conference Record of the 2008 IEEE International Symposium on Electrical Insulation, June 9-12, 2008, Vancouver, Canada. Piscataway:IEEE Press, 2008:547-550. http://ieeexplore.ieee.org/document/4570392/ |
 2013, Vol. 36
2013, Vol. 36

