滑模变结构控制作为一类特殊的非线性控制,对系统内部参数的摄动和外部的扰动作用具有鲁棒性[1-3],能保证系统的性能达到期望品质,因而在许多领域如机器人[4]、电机[5]和航空航天[6]领域有着广泛应用。但在实际应用中,由于变结构控制固有抖振的存在,使得控制性能受到不利影响,甚至使系统产生振荡或失稳,以至损坏系统部件。因此,关于变结构控制抖振消除的研究成为了变结构控制研究的首要问题。为了从理论上消除或削弱抖振,众多学者作了大量研究,从不同的角度提出了解决方法[7-9]。
通常,滑模变结构控制系统的运动分为趋近运动和滑动模态运动2个阶段。趋近运动阶段应由到达条件保证系统运动在有限时间内从任意初始状态到达切换面;滑动模态阶段系统在控制律作用下保持滑模运动。由于变结构控制的优点在于其滑动模态具有鲁棒性,即系统只在滑动阶段才具有对满足匹配条件的系统参数摄动和外扰动具有不变性,若能加快趋近运动,缩短滑模到达时间,将能有效地改善系统的动态性能。因而,缩短到达时间以增强系统对不确定性的鲁棒性成为变结构控制的又一重要研究方向。文献[10]通过设计一种动态非线性切换函数,使控制器在稳定条件下,具有全局鲁棒性。文献[11]研究了连续系统的全程滑模变结构控制,文献[12]针对离散系统设计了离散系统的全程滑模控制。通过选择切换函数使系统相轨迹从初始状态开始就位于切换面上,并通过控制律的作用使系统状态始终保持沿切换面附近运动,从根本上消除了趋近运动段,克服了传统变结构控制中趋近运动段不具有鲁棒性的特点,从而使系统具有全局鲁棒性。但全程滑模变结构控制的局限性在于要求知道系统初始状态,若初始状态未知,则仍不能消除趋近运动段,因而研究缩短趋近运动段时间即到达时间仍具重要意义。高为炳提出趋近律[13-14]概念,尽管不能具体刻画出趋近运动的过程或算出某些品质指标,但可以间接对趋近运动的品质给出一个评价。以指数趋近律ṡ=-ks-εsgn(s)为例,通过调整趋近律参数k和ε,使其既能保证滑动模态到达过程的动态品质,又能削弱系统控制信号的高频抖振。文献[15]在传统高氏趋近律基础上提出一种新型趋近律,尽可能地减小抖振并加快了趋近速度。笔者分析了传统高氏趋近律[13-14]和文献[15]所提趋近律的优缺点,并在此基础上提出了连续时间系统滑模变结构控制的一种改进的趋近律,以切换函数绝对值|s|=1为分界点分别采用不同的趋近律。新的趋近律进一步缩短了到达时间,又能大幅削弱控制器输出的抖振,改善了系统运动的动态性能,增强了系统的鲁棒性。
1 传统趋近律分析1) 等速趋近律
| $ \dot s = - \varepsilon {\mathop{\rm sgn}} \left( s \right),\varepsilon > 0, $ | (1) |
式中,常数ε表示系统状态点趋近切换面s=0的速率。ε小,趋近速度慢,导致控制的过渡过程变长;ε大,则状态点到达切换面时将具有较大的速度,引起的抖振也较大。
2) 指数趋近律
| $ \dot s = - ks - \varepsilon {\mathop{\rm sgn}} \left( s \right),k > 0,\varepsilon > 0, $ | (2) |
该趋近律由指数趋近项-ks和等速趋近项-εsgn(s)两部分构成。单独考虑指数趋近项时,由ṡ=-ks得其解为s(t)=s(0)e-kt。此时,趋近速度从初始值逐步减小直至趋于零。对单纯的指数趋近项-ks而言,系统状态趋向切换面是一个渐近的过程,不能保证有限时间内到达切换面,切换面上也就不存在滑动模态了,所以要增加一个等速趋近项-εsgn(s),使得当s接近于零时,趋近速度是ε而不是零,可以保证系统状态点于有限时间到达切换面。为保证快速趋近的同时削弱抖振,应在增大k的同时减小ε,但等速项εsgn(s)的存在使系统从理论上仍无法消除抖振。
3) 幂次趋近律
| $ \dot s = - k{\left( s \right)^\alpha }{\mathop{\rm sgn}} \left( s \right),k > 0,0 < \alpha < 1, $ | (3) |
该趋近律的趋近速度为k|s|α,距切换面越近,速度越慢,与等速趋近律的固定趋近速度相比,有效地降低了抖振。幂次趋近律能够实现平滑进入滑动模态,但趋近速度较慢。
2 改进的趋近律 2.1 改进趋近律的提出文献[15]结合指数趋近律式(2)和幂次趋近律式(3)提出如下趋近律
| $ \begin{array}{l} \dot s = - k{\left| s \right|^\beta }s - \varepsilon {\left| s \right|^\alpha }{\mathop{\rm sgn}} \left( s \right),\\ \left( {k > 0,\varepsilon > 0,0 < \alpha < 1,0 < \beta < 1} \right)。\end{array} $ | (4) |
该趋近律既能快速趋近滑动模态,又保留了幂次趋近律能够平滑进入滑动模态的优点。但与指数趋近律相比,在趋近速度上仍有不足之处。其不足之处在于,不考虑切换项的情况下,|s|<1时,趋近速度反倒不及传统的指数趋近律。对此分析如下:指数趋近律式(2)和趋近律式(4)中,切换项增益都不会太大以避免大的抖振,趋近速度主要取决于ks(指数趋近律式(2))和k|s|βs(趋近律式(4))。指数趋近律中,k为常数。随着|s|的减小,趋近速度ks从初始值逐步趋于0。同样,趋近律式(4)中,趋近速度k|s|βs随|s|的减小而自适应地减小并趋于0。s>1时,k|s|βs>|ks|,趋近律式(4)的趋近速度快于指数趋近律;|s|=1时,k|s|βs=|ks|,二者速度相等;|s|<1时,|k|s|βs|<|ks|,趋近律式(4)的趋近速度比指数趋近律慢。
基于以上分析,结合指数趋近律式(2)、幂次趋近律式(3)和趋近律式(4),提出一种改进的新型趋近律如下
| $ \begin{array}{l} \dot s = - k{\left| s \right|^{\beta {\mathop{\rm sgn}} \left( {\left| s \right| - 1} \right)}}s - \varepsilon {\left| s \right|^\alpha }{\mathop{\rm sgn}} \left( s \right),\\ \left( {k > 0,\varepsilon > 0,0 < \alpha < 1,0 < \beta < 1。} \right) \end{array} $ | (5) |
改进的新型趋近律与趋近律式(4)的不同之处在于,将指数β替换为βsgn(|s|-1)。当|s|>1,新型趋近律即是趋近律式(4);当|s|≤1时,在不考虑切换项的情况下,新型趋近律的趋近速度为k|s|-βs,与趋近律式(4)此时的趋近速度k|s|βs相比,显然有|k|s|βs|>|k|s|βs|。因而,系统从初始状态趋向滑动模态的整个过程中,新型趋近律的趋近速度始终要快于指数趋近律式(2)和趋近律式(4)。同时,由于s趋于0时,k|s|-βs相应趋于0,因而,新型趋近律也保持了指数趋近律式(2)和趋近律式(4)的优点,即进入滑动模态时速度渐缓,有利于降低抖振。
2.2 新型趋近律的滑模稳定性分析取Lyapunov函数为
| $ V\left( x \right) = \frac{1}{2}{s^2}。$ |
则有
| $ \begin{array}{l} \dot V\left( x \right) = s\dot s = \\ s\left( { - k{{\left| s \right|}^{\beta {\mathop{\rm sgn}} \left( {\left| s \right| - 1} \right)}}s - \varepsilon {{\left| s \right|}^\alpha }{\mathop{\rm sgn}} \left( s \right)} \right) = \\ - k{\left| s \right|^{\beta {\mathop{\rm sgn}} \left( {\left| s \right| - 1} \right)}}{s^2} - \varepsilon {\left| s \right|^{\alpha + 1}} \le 0。\end{array} $ |
因此,新型趋近律式(5)满足滑模到达条件。
2.3 新型趋近律的到达时间计算到达时间的计算分2种情况,即切换函数初始值|s(0)|≤1还是|s(0)|>1。
2.3.1 |s(0)|≤1的情况切换函数初始值|s(0)|≤1时,由式(5)可知此时的趋近律即为
| $ \dot s = - k{\left| s \right|^{ - \beta }}s - \varepsilon {\left| s \right|^\alpha }{\mathop{\rm sgn}} \left( s \right)。$ | (6) |
若切换函数初始值0<s(0)≤1,则
| $ \dot s = - k{s^{1 - \beta }} - \varepsilon {s^\alpha }, $ |
若1-β=α即α+β=1,则上式变为
| $ \dot s = - \left( {k + \varepsilon } \right){s^\alpha }, $ |
即
| $ {s^{ - \alpha }}\dot s = - \left( {k + \varepsilon } \right), $ |
对上式2边从0到t积分得
| $ \frac{{{s^{1 - \alpha }}\left( t \right) - {s^{1 - \alpha }}\left( 0 \right)}}{{1 - \alpha }} = - \left( {k + \varepsilon } \right)t。$ |
到达切换面时s(t)=0,因而由上式得到从初始状态到达切换面的到达时间为
| $ t = \frac{{{s^{1 - \alpha }}\left( 0 \right)}}{{\left( {1 - \alpha } \right)\left( {k + \varepsilon } \right)}} = \frac{{{s^\beta }\left( 0 \right)}}{{\beta \left( {k + \varepsilon } \right)}}, $ | (7) |
一般情况下不满足1-β=α即α+β=1,此时无法得到到达时间的解析解。
若切换函数初始值-1≤s(0)<0,可类似得出α+β=1时到达时间为
| $ t = \frac{{{{\left( { - s} \right)}^\beta }\left( 0 \right)}}{{\beta \left( {k + \varepsilon } \right)}}, $ | (8) |
由上式可得出切换函数初始值|s(0)|≤1时,到达时间的统一表达式为
| $ t = \frac{{{{\left| {s\left( 0 \right)} \right|}^\beta }}}{{\beta \left( {k + \varepsilon } \right)}}。$ | (9) |
切换函数初始值|s(0)|>1时,到达过程分为2个阶段。第一阶段为系统由初始状态向切换面运动,经过t1时长后切换函数|s(t1)|=1;第二阶段为系统由切换函数为|s(t1)|=1处继续向切换面运动,经过t2时长后到达切换面,趋近运动段的到达时间为t1+t2。
由式(5)可知第一阶段系统依照的趋近律即为文献[15]所提的趋近律式(4),重写如下
| $ \dot s = - k{\left| s \right|^{ - \beta }}s - \varepsilon {\left| s \right|^\alpha }{\mathop{\rm sgn}} \left( s \right), $ |
切换函数初始值s(0)>1时,上式即为
| $ \dot s = - k{s^{1 + \beta }} - \varepsilon {s^\alpha }。$ |
文献[15]就上面的微分方程得出到达时间的解析解为
| $ t = \frac{{{s^{1 - \alpha }}\left( 0 \right)}}{{\varepsilon \left( {1 - \alpha } \right)}} + \frac{{k{s^{\beta - \alpha + 2}}\left( 0 \right)}}{{\varepsilon \left( {\beta - \alpha + 2} \right)}}。$ | (10) |
此处特别指出,实际上此微分方程无解析解,式(10)是一个错误解。切换函数初始值s(0)<-1时,同样得不到到达时间的解析解。
第二阶段依照的趋近律为式(6),若满足α+β=1则趋近运动所用时间t2由式(9)可计算得
| $ {t_2} = \frac{1}{{\beta \left( {k + \varepsilon } \right)}}。$ |
因此,总的来说,|s(0)|>1时只有在满足条件α+β=1时才能求得到达时间的部分解析解,其他情况下无法得到到达时间的解析解。
3 仿真算例倒立摆系统的控制问题一直是控制研究中的一个典型问题,考虑台车式倒立摆模型状态方程[16]如下
| $ \mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{A}}x + \mathit{\boldsymbol{B}}\left( {u + f\left( t \right)} \right)。$ | (11) |
其中
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 0&0&1&0\\ 0&0&0&1\\ 0&{{a_{32}}}&0&0\\ 0&{{a_{42}}}&0&0 \end{array}} \right],\mathit{\boldsymbol{B = }}\left[ {\begin{array}{*{20}{c}} 0\\ 0\\ {{b_3}}\\ {{b_4}} \end{array}} \right],\mathit{\boldsymbol{x = }}\left[ {\begin{array}{*{20}{c}} x\\ \theta \\ {\dot x}\\ {\dot \theta } \end{array}} \right], $ |
且
| $ {a_{32}} = - 3\left( {{C_1} - mga} \right)/\left[ {a\left( {4M + m} \right)} \right]; $ |
| $ {a_{12}} = - \frac{{3\left( {M + m} \right)\left( {{C_1} - mga} \right)}}{{{a^2}m\left( {4M + m} \right)}}; $ |
| $ {b_3} = 4/\left( {4M + m} \right); $ |
| $ {b_4} = 3/\left( {4M + m} \right), $ |
其中:M为小车质量;m为摆的质量;2a为杆长;x为小车位置;θ为摆的角度;C1为弹性硬度;g=9.8 m/s2;u和f(t)分别为控制输入和干扰力,且|f(t)|≤f0;f0为常数。控制的目标是通过给小车底座施加一个控制量,使小车停留在预定的位置,并使杆不倒下,即不超过预先定义好的垂直偏离角度范围。
取切换函数为s=CX=c1x+c2θ+c3ẋ+c4
取初始状态为x(0)=0.5,θ(0)=0.3,ẋ(0)=0,
取切换面参数C=[-4.767 3,48.356 4,-8.740 1,18.653 4]。
取趋近律参数为α=0.3,β=0.9,k=ε=3。
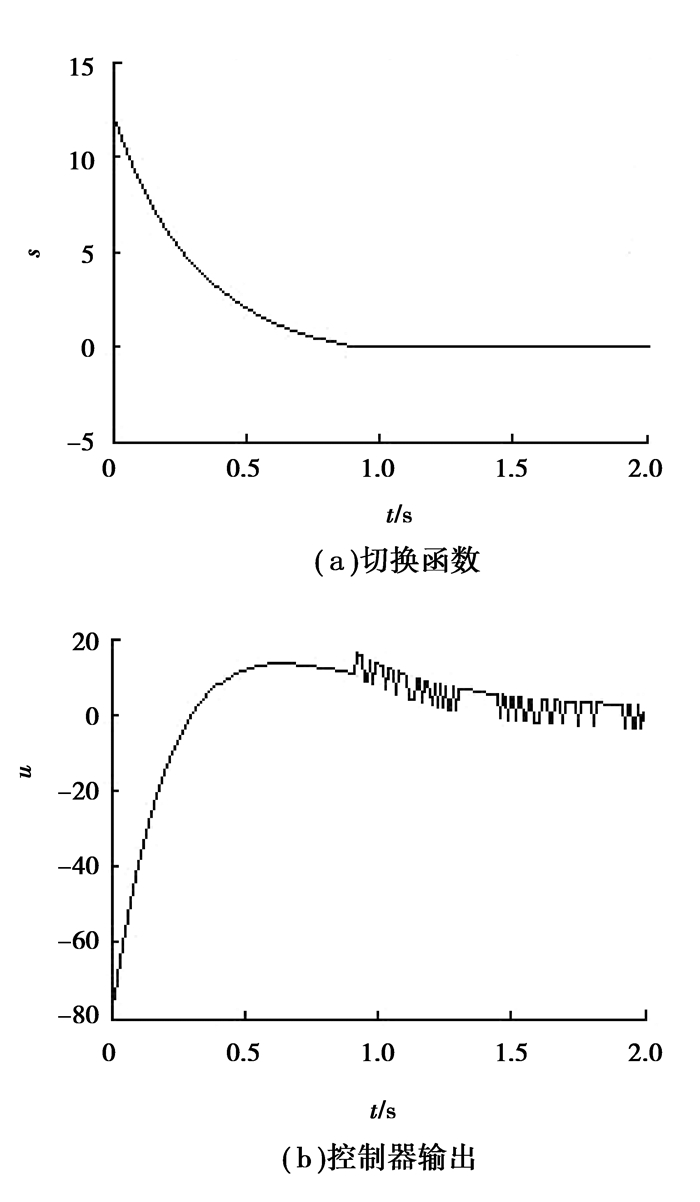
|
图 1 趋近律式(2)的仿真结果 |
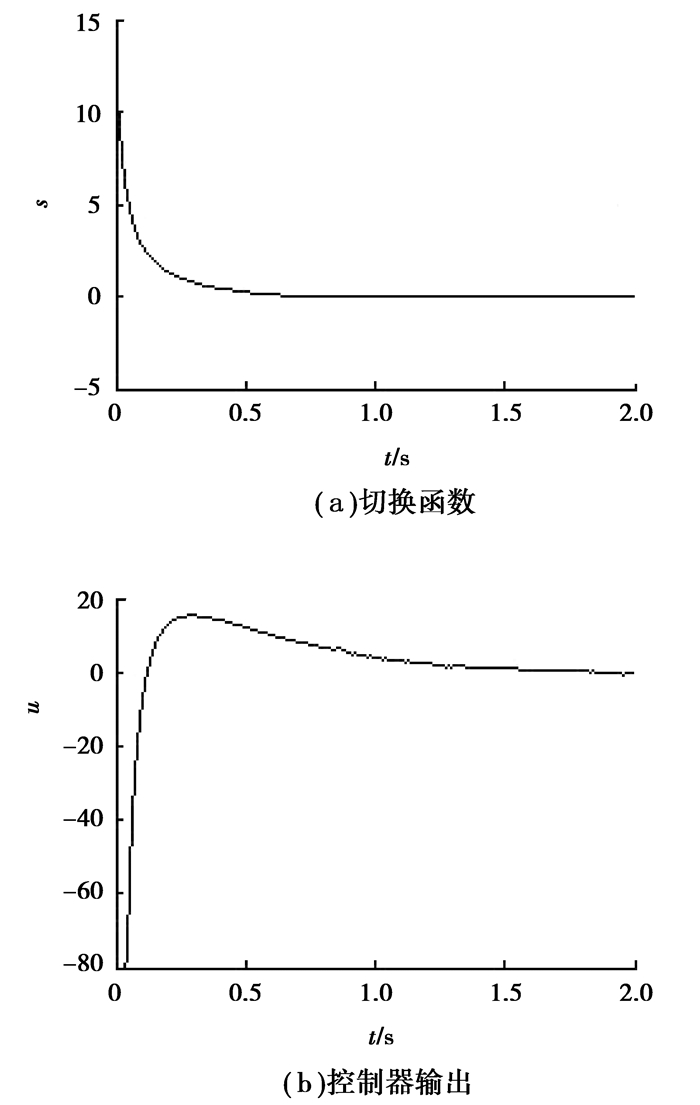
|
图 2 趋近律式(4)的仿真结果 |
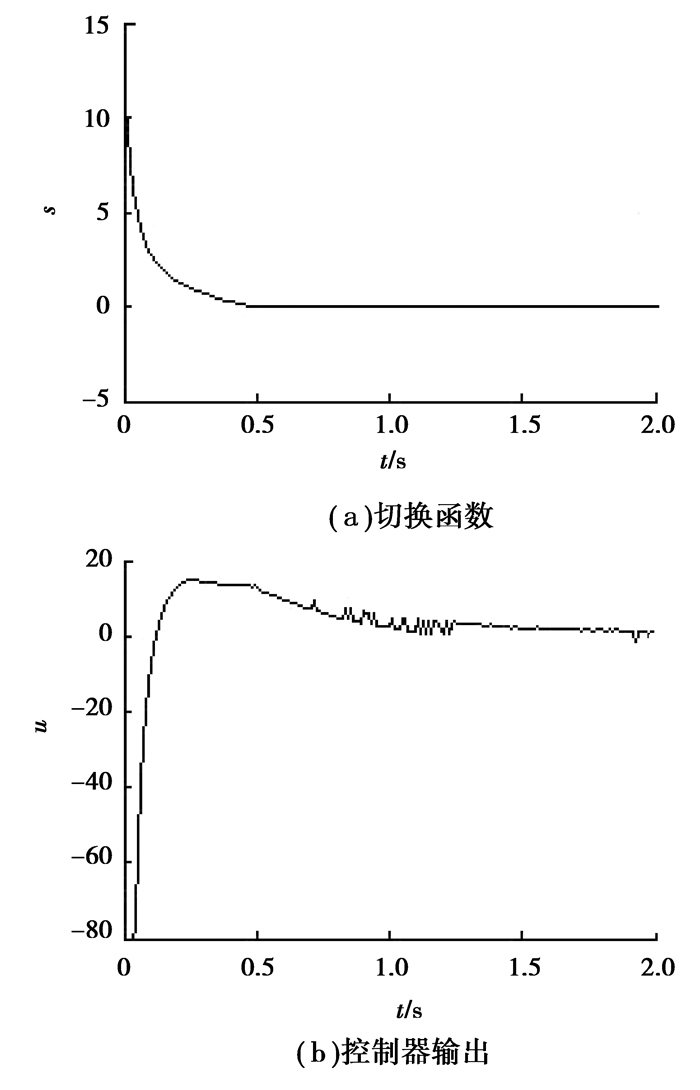
|
图 3 趋近律式(5)的仿真结果 |
由仿真结果可以看到,从趋近运动快慢来说,采用给出的新型趋近律式(5),系统状态到达切换面的速度最快,到达时间最短,不到0.5 s;文献[15]中的趋近律式(4),其趋近速度稍慢,到达时间约为0.65 s;指数趋近律式(4)的趋近速度最慢,到达时间约为0.9 s。从控制器输出来说,图 1的指数趋近律式(2),其控制器输出始终存在较大的带状抖振;图 2的趋近律式(4)无明显抖振,给出的新型趋近律式(5),其控制器输出有轻微抖振现象,这是由于快速趋近所引起的。总的来说,采用给出的新型趋近律设计变结构控制,既能大幅削弱了控制器输出的抖振,同时能使系统状态快速到达切换面,缩短了到达时间,改善了系统动态品质,增强了系统鲁棒性。
4 结论针对传统趋近律及其改进型的优缺点,提出了一种改进的趋近律,并在满足一定条件的情况给出了到达时间的解析式。对新型趋近律和传统趋近律就趋近运动速度作了理论上的分析,并利用台车式倒立摆模型作了仿真。理论分析和仿真结果表明,新型趋近律具有趋近速度快且能大幅削弱抖振的优点,表明了本文给出的趋近律的有效性。
| [1] | Utkin V, Guldner J, Shi J X. Sliding mode control in electromechanical systems[M]. 2nd ed. London: Taylor & Francis, 1999. |
| [2] | Hirschorn R. Sliding-mode control variations[J]. IEEE Transactions on Automatic Control, 2007, 52(3): 468–480. DOI:10.1109/TAC.2007.892372 |
| [3] | Chen M S, Chen C H, Yang F Y. An LTR-observer-based dynamic sliding mode control for chattering reduction[J]. Automatica, 2007, 43(6): 1111–1116. DOI:10.1016/j.automatica.2006.12.001 |
| [4] |
徐雪梅, 张均富.
球面2自由度机器人的滑模变结构控制[J]. 四川大学学报:工程科学版, 2011, 43(6): 232–237.
XU Xuemei, ZHANG Junfu. Sliding mode variable structure control of spherical 2-DOF robots[J]. Journal of Sichuan University:Engineering Science Edition, 2011, 43(6): 232–237. (in Chinese) |
| [5] |
汪海波, 周波, 方斯琛.
永磁同步电机调速系统的滑膜控制[J]. 电工技术学报, 2009, 24(9): 71–77.
WANG Haibo, ZHOU Bo, FANG Sichen. Sliding mode controller for PM synchronous motor drive[J]. Transactions of China Electrotechnical Society, 2009, 24(9): 71–77. (in Chinese) |
| [6] |
张景瑞, 张威泰, 曾祥远, 等.
考虑不确定性的航天器姿态滑模控制器设计[J]. 北京理工大学学报, 2011, 31(10): 1198–1202.
ZHANG Jingrui, ZHANG Weitao, ZENG Xiangyuan, et al. Robust controller design for the attitude control of spacecraft with uncertainty[J]. Journal of Beijing Institute of Technolotgy, 2011, 31(10): 1198–1202. (in Chinese) |
| [7] | Slotine J J, Sastry S S.Tracking control of non-linear systems using sliding surfaces with application to robot manipulator[C]//Proceedings of the 1983 IEEE American Control Conference, June 22-24, 1983, San Francisco, CA, USA. Piscataway:IEEE Press, 1983:132-135. |
| [8] | Burton J A, Zinober A S I. Continuous approximation of variable structure control[J]. International Journal of Systems Science, 1986, 17(6): 875–885. DOI:10.1080/00207728608926853 |
| [9] | Chung S C Y, Lin C L L. A transformed lure problem for sliding mode control and chattering reduction[J]. IEEE Transactions on Automatic Control, 1999, 44(3): 563–568. DOI:10.1109/9.751351 |
| [10] | Lu Y S, Chen J S. Design of a global sliding-mode controller for a motor drive with bounded control[J]. International Journal of Control, 1995, 62(5): 1001–1019. DOI:10.1080/00207179508921579 |
| [11] |
张科, 周凤岐.
不确定性多变量系统的全程滑模变结构控制方案设计[J]. 控制理论与应用, 1999, 16(2): 221–224.
ZHANG Ke, ZHOU Fengqi. Design of global sliding-mode variable structure control for uncertain multivariable linear systems[J]. Control Theory and Applications, 1999, 16(2): 221–224. (in Chinese) |
| [12] |
米阳, 李文林, 井元伟, 等.
线性多变量离散系统全程滑模变结构控制[J]. 控制与决策, 2003, 18(4): 460–463, 467.
MI Yang, LI Wenlin, JING Yuanwei, et al. Global sliding mode control for uncertain discrete time systems[J]. Control and Decision, 2003, 18(4): 460–463, 467. (in Chinese) |
| [13] | Hung J Y, Gao W B, Hung J C. Variable structure control:a survey[J]. IEEE Transactions on Industrial Electronics, 1993, 40(1): 2–22. DOI:10.1109/41.184817 |
| [14] | 高为炳. 变结构控制的理论及设计方法[M]. 北京: 科学出版社, 1996. |
| [15] |
姜君, 陈庆伟, 郭健, 等.
基于新型趋近律的动中通系统滑模稳定跟踪控制[J]. 控制与决策, 2011, 26(12): 1904–1908.
JIANG Jun, CHEN Qingwei, GUO Jian, et al. Sliding mode stable tracking control for mobile satellite communication system based on a new reaching law[J]. Control and Decision, 2011, 26(12): 1904–1908. (in Chinese) |
| [16] | 刘金琨. 滑模变结构控制MATLAB仿真[M]. 北京: 清华大学出版社, 2005. |
 2013, Vol. 36
2013, Vol. 36

