2. 商丘师范学院, 河南 商丘 476000
2. Shangqiu Normal University, Shangqiu, Henan 476000, China
基于曲线演化和水平集方法的活动轮廓模型[1]是当前研究灰度非匀质图像分割的热点,其不仅使分割物体具有封闭、光滑的边界,而且演化曲线能自适应拓扑结构变化(如拆分、合并)。一般可分为:边界模型[2]、区域模型[3]。边界模型利用梯度信息确定物体边界,如地测线活动轮廓[2]。虽然能分割灰度非匀质图像,但对噪声、弱边缘或不连续边较敏感。区域模型利用同质区域信息相似性,吸引轮廓线定位于物体边界,如分片常量Chan-Vese(CV)模型[3]。但分片匀质的统计假设,使其无法分割灰度非匀质图像。
为此,一些结合局部统计信息的区域活动轮廓模型被提出。LI Chun-Ming等[4]利用尺度可伸缩的核函数去捕获图像局部信息,提出局部二值拟合(Local binary fitting,LBF)的算法。但模型计算复杂,且对初始轮廓线比较敏感。LANKON S等[5]直接统计中心点圆形区域内局部均值,提出基于局部区域的CV模型(LCV)。ZHANG Kai-Hua等[6]利用局部图像拟合(Local image fitting,LIF)能量,对LBF进行简化,并通过高斯卷积核实现水平集函数的正则化,但计算代价仍然较高。王利等[7]基于局部二值模型,采用多相水平集拟合局部灰度。刘建磊等[8]利用图像经过高斯滤波后的梯度信息,定义分割能量函数,但梯度信息对噪声很敏感。LIU Shi-gang等[9]提出一种使用退化的CV模型作为初始轮廓的局部区域活动轮廓模型,但增加了计算复杂度。上述方法均是采用基于水平集的数值解法,加之在每个局部区域都要进行水平集函数的迭代运算,使得运算代价高昂且极易陷入局部最小。因而,近年来,出现许多非水平集数值解法的研究。EI-ZEHIRY N等[10]基于栅格图的最大流算法计算CV模型全局最优解,不仅降低了计算代价,还增强对初始轮廓线的鲁棒性,但与CV一样,无法分割灰度非匀质图像。
针对以上问题,提出一种基于局部区域活动轮廓模型快速非匀质图像分割新方法。首先通过计算核函数与灰度非匀质图像的卷积,捕获图像的局部区域特征;然后,结合割测度定义全局正则性,有效约束演化曲线正确定位于物体边界;最后,基于栅格加权图的最大流算法实现演化曲线内外顶点的二值标注,进而获得物体的边缘轮廓。
1 基于区域的活动轮廓模型假设图像域Ω⊂R2是有界的Lipschitz域。图像I:Ω→R为灰度图像。Mumford和Shan[12]忽略单一物体的表面纹理细节,把图像I近似为分片光滑函数,定义能量泛函为
| $ {E_{MS}}\left( {u,C} \right) = \int_\mathit{\Omega } {{{\left( {u - I} \right)}^2}{\rm{d}}x} + \mu \int_{\mathit{\Omega \backslash C}} {{{\left| {\nabla u} \right|}^2} + v\left| C \right|} , $ | (1) |
其中,|C|是轮廓的长度,该能量泛函的最小化能获得分割图像的最佳轮廓C和逼近源图像I的图像u。使得被分割的各子区域内平滑且保持不连续边界。但由于C和u未知,且EMS是非凸泛函,故其最小化是个难题。为此,Chan和Vese[3]提出能量泛函EMS的简化形式,CV模型,即把图像近似为分片常值函数。其能量泛函定义为
| $ \begin{array}{l} {E_{CV}}\left( {C,{c_1},{c_2}} \right) = {\lambda _1}\int_{{\rm{in}}\left( C \right)} {{{\left| {I\left( x \right) - {c_1}} \right|}^2}{\rm{d}}x} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\lambda _2}\int_{{\rm{out}}\left( C \right)} {{{\left| {I\left( x \right) - {c_2}} \right|}^2}{\rm{d}}x} + \nu \left| C \right|, \end{array} $ | (2) |
其中,c1和c2各自表示在轮廓内in(C)和外out(C)的灰度均值。利用水平集方法,轮廓线C被表示为水平集函数(的零水平集C={x((|((x)=0},从而,把泛函ECV的最小化问题,转化为水平集演化方程的数值计算[3]。但是CV模型的分片均值的统计假设,使其无法正确分割灰度非匀质图像(如图 1b列所示)。为克服上述局限,LANKON S等[7]提出基于局部区域的CV模型(LCV)。首先用符号函数B(x,y)掩模图像I的局部区域

|
图 1 传统模型和新方法的演化结果 |
| $ B\left( {x,y} \right) = \left\{ \begin{array}{l} 1,\left\| {x - y} \right\| < r,\\ 0,其他, \end{array} \right. $ | (3) |
在中心点x被B(x,y)掩模的局部区域内,演化曲线内外的灰度均值cx1和cx2被表示为
| $ \left. \begin{array}{l} {c_{x1}} = \frac{{\int_{{\mathit{\Omega }_y}} {B \cdot H\varphi \left( y \right) \cdot I\left( y \right){\rm{d}}y} }}{{\int_{{\mathit{\Omega }_y}} {B \cdot H\varphi \left( y \right){\rm{d}}y} }}\\ {c_{x2}} = \frac{{\int_{{\mathit{\Omega }_y}} {B \cdot \left( {1 - H\varphi \left( y \right)} \right) \cdot I\left( y \right){\rm{d}}y} }}{{\int_{{\mathit{\Omega }_y}} {B \cdot \left( {1 - H\varphi \left( y \right)} \right){\rm{d}}y} }} \end{array} \right\}。$ | (4) |
然后,定义局部区域能量泛函如下
| $ \begin{array}{l} {E_{LCV}}\left( \varphi \right) = \int_{{\mathit{\Omega }_x}} {\delta \varphi \left( x \right)} \left[ {\int_{{\mathit{\Omega }_y}} {B\left( {H\varphi \left( y \right)\left( {I\left( y \right) - } \right.} \right.} } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\left. {{{\left. {{c_{x1}}} \right)}^2} + \left( {1 - H\varphi \left( y \right)} \right){{\left( {I\left( y \right) - {c_{x2}}} \right)}^2}} \right)} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\lambda \int_{{\mathit{\Omega }_x}} {\delta \varphi \left( x \right)\left\| {\nabla \varphi \left( x \right)} \right\|{\rm{d}}x} , \end{array} $ | (5) |
其中,H是Heaviside函数,δ是Dirac的delta且函数δ(ϕ)=H′(ϕ)。LCV模型的局部特征捕获能力,使之能分割灰度非匀质图像(图 1c列上))。最后,根据一阶变分,推导出曲线演化的水平集演化方程
| $ \begin{array}{*{20}{c}} {\frac{{\partial \varphi }}{{\partial t}}\left( x \right) = \delta \varphi \left( x \right)\int_{{\mathit{\Omega }_y}} {B \cdot \delta \varphi \left( y \right) \cdot } }\\ {\left( {{{\left( {I\left( y \right) - {c_{x1}}} \right)}^2} - {{\left( {I\left( y \right) - {c_{x2}}} \right)}^2}} \right){\rm{d}}y + }\\ {\lambda \delta \varphi \left( x \right){\rm{div}}\left( {\frac{{\nabla \varphi \left( x \right)}}{{\left| {\nabla \varphi \left( x \right)} \right|}}} \right),} \end{array} $ | (6) |
式(6)方程本质上是局部沿着轮廓边界C=ϕ-1(0)计算的。虽然正则化的δε能扩大计算带宽,但计算仍然沿着指定带宽的C在窄带上执行。因此,演化曲线容易收敛到局部极值,且对初始轮廓线位置敏感。如分割多灰阶物体的非匀质图像(图 1c列下)。
2 提出的灰度非匀质图像分割方法针对上述全局和局域CV模型的缺陷,结合核函数和割测度,基于局部区域活动轮廓模型提出一种非匀质图像的组合优化分割方法。
2.1 定义能量函数首先,假设给定图像域Ω为二维网格空间z2,从而对于任意像素x∈Ω,可以定义一个二值变量,
| $ \gamma \left( x \right) = \left\{ \begin{array}{l} 1,x\;在轮廓内,\\ 0,其他。\end{array} \right. $ | (7) |
因此,通过对离散像素格上像素点x的二值标注γ(x)可以隐含表示演化轮廓,如in(C)=γ-1(1)。
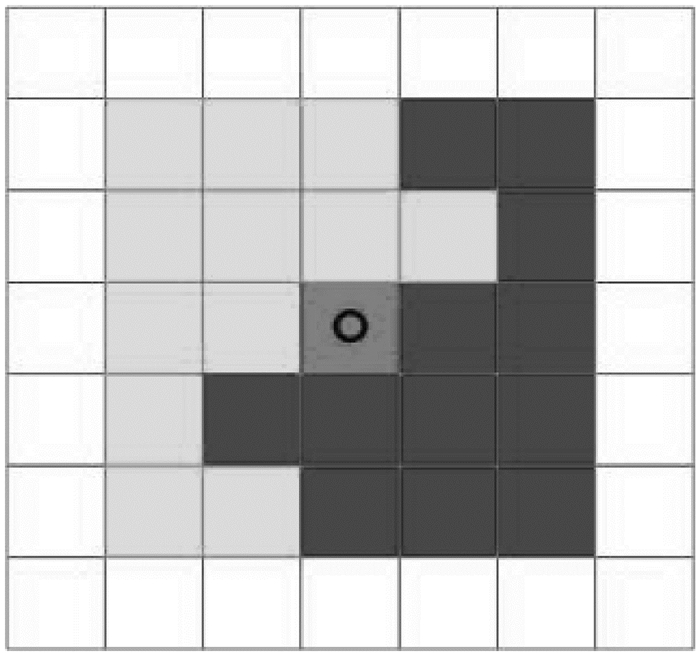
为有效处理图像的非匀质灰度分布现象,基于离散像素格上的局部连通结构统计局部特征。如图 2着色区域所示,其中中心灰方格点代表中心点x,邻域取作以其为中心的5×5方形区域,用y表示x的邻近像素,浅灰色点表示轮廓外的点,即γ(y)=0;深色点表示轮廓内的点,即γ(y)=1。但由于像素中心点x的邻近像素对局部特征的贡献随着远离中心点而减少。为此,引入区域加权核函数,类似于文献[4],研究选择高斯核函数如下
|
图 2 局部连通结构 |
| $ {g_k}\left( {x - y} \right) = \frac{1}{{2{\rm{ \mathsf{ π} }}{\sigma ^2}}}{e^{ - {{\left| {x - y} \right|}^2}/2{\sigma ^2}}}, $ | (8) |
其中:σ是尺度参数;当|x-y|>3σ时,gk(x-y)减少到接近于零。因此,不仅能利用尺度参数σ间接控制中心点x的邻近范围:{y:|x-y|≤3σ},还能用gk(x-y)作为邻近点y在局部特征统计中的权重。进一步,在中心点x被gk(x-y)掩模的局部区域内,定义曲线内外的灰度均值函数c1(x)和c2(x)为
| $ \left. \begin{array}{l} {c_1}\left( x \right) = \frac{{\sum\nolimits_{x \in \mathit{\Omega }} {{g_k}\left( {x - y} \right)I\left( y \right)\gamma \left( y \right)} }}{{\sum\nolimits_{x \in \mathit{\Omega }} {{g_k}\left( {x - y} \right)\gamma \left( y \right)} }}\\ {c_2}\left( x \right) = \frac{{\sum\nolimits_{x \in \mathit{\Omega }} {{g_k}\left( {x - y} \right)I\left( y \right)\left( {1 - \gamma \left( y \right)} \right)} }}{{\sum\nolimits_{x \in \mathit{\Omega }} {{g_k}\left( {x - y} \right)\left( {1 - \gamma \left( y \right)} \right)} }} \end{array} \right\}, $ | (9) |
其中:c1(x)表示位于轮廓内的点(图 2蓝色点)的加权均值;c2(x)表示轮廓外的点(图 2绿色点)的加权均值。则局部拟合图像表示为:I(x)=c1(x)γ(x)+c2(x)(1-γ(x))。为此,在局部连通结构上,定义局部拟合数据能量为
| $ \begin{align} {E_x}\left( {{c_1}\left( x \right),{c_2}\left( x \right)} \right) =& {\lambda _1}{\left( {I\left( x \right) - {c_1}\left( x \right)} \right)^2}\gamma \left( x \right) + \\ &{\lambda _2}{\left( {I\left( x \right) - {c_2}\left( x \right)} \right)^2}\left( {1 - \gamma \left( x \right)} \right), \end{align} $ | (10) |
其中,λ1,λ2是合适的权重常数,对于整个栅格图像域,假设各局部特征都是独立的,给定轮廓C,并用轮廓线长度|C|正则化演化曲线,因此,特征分布的整体能量函数定义为
| $ E\left( {\gamma \left( x \right)} \right) = \sum\nolimits_{x \in \mathit{\Omega }} {{E_x}\left( {{c_1}\left( x \right),{c_2}\left( x \right)} \right)} + \mu \left| C \right|, $ | (11) |
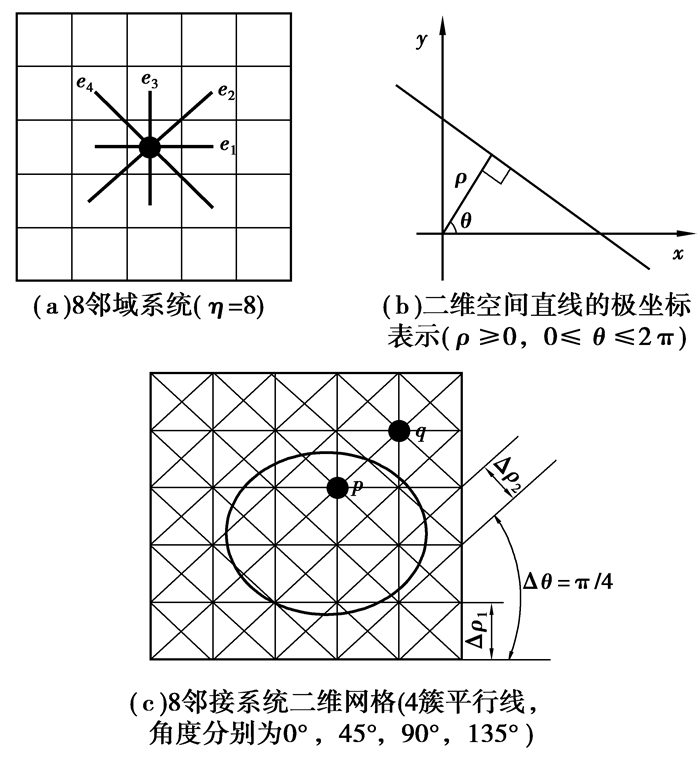
其中,μ是正则项权重常数。文献[11]证明了基于栅格图的割测度能逼近欧氏长度度量,而割测度的几何属性被图的邻接系统和边权重所决定。定义8邻接系统η=8,设网格点距为单位1,邻接边对称(如图 3a),则边集Γk={ e1,e2,e3,e4},邻接边长度|e1|=|e3|=1;|e2|=|e4|=
|
图 3 割测度几何属性 |
| $ \left| C \right| = \frac{1}{2}\sum\limits_k {{n_k}\frac{{\Delta \theta }}{{{\eta ^2}\left| {{e_k}} \right|}}} 。$ | (12) |
在邻接单元中,|ek|表示第k条邻接边的长度,Δθ表示角度变化(Δθ=π/4)。nk表示第k个邻接边与轮廓C的交点数。为不与上述的局部区域混淆,对计算长度项的邻接系统,用p表示中心点,q表示其邻接点。由于分割为二值标注,则易知仅仅当γ(p)和γ(q)有不同标注时,邻接边与轮廓才相交(如图 3c中的格点p,q与轮廓C)。因此,定义边与轮廓相交点数的检测函数如下
| $ \begin{array}{*{20}{c}} {d\left( {p,q} \right) = \gamma \left( p \right)\left( {1 - \gamma \left( q \right)} \right) + \gamma \left( q \right)\left( {1 - \gamma \left( p \right)} \right) = }\\ {\gamma \left( p \right) + \gamma \left( q \right) - 2\gamma \left( p \right)\gamma \left( q \right),} \end{array} $ | (13) |
同时,令
| $ \left\| C \right\| = \frac{1}{2}\sum\limits_{{e_{pq}} \in {\mathit{\Gamma }_k}} {d\left( {p,q} \right){w_{pq}}} , $ | (14) |
插入式(13)、(14)后,栅格图像的能量函数可完整定义为
| $ \begin{align} E\left( {\gamma ,{c_1},{c_2}} \right) =& {\lambda _1}\sum\nolimits_{x \in \mathit{\Omega }} {{{\left( {I\left( x \right) - {c_1}\left( x \right)} \right)}^2}\gamma \left( x \right)} + \\ &{\lambda _2}\sum\nolimits_{x \in \mathit{\Omega }} {{{\left( {I\left( x \right) - {c_2}\left( x \right)} \right)}^2}\left( {1 - \gamma \left( x \right)} \right)} + \\ &\mu \sum\limits_{{e_{pq}} \in {\mathit{\Gamma }_k}} {\left( {\gamma \left( p \right) + \gamma \left( q \right) - 2\gamma \left( p \right)\gamma \left( q \right)} \right){w_{pq}}} 。\end{align} $ | (15) |
式(16)数据项Ex和正则项Epq可分别记为
| $ \left. \begin{array}{l} {E_x}\left( {\gamma \left( x \right)} \right) = {\lambda _1}{\left( {I\left( x \right) - {c_1}\left( x \right)} \right)^2}\gamma \left( x \right) + \\ {\lambda _2}{\left( {I\left( x \right) - {c_2}\left( x \right)} \right)^2}\left( {1 - \gamma \left( x \right)} \right),\\ {E_{pq}}\left( {\gamma \left( p \right),\gamma \left( q \right)} \right) = \left( {\gamma \left( p \right) + \gamma \left( q \right)} \right) - \\ \left. {2\gamma \left( p \right)\gamma \left( q \right)} \right){w_{pq}} \end{array} \right\}。$ | (16) |
对于Epq项,wpq(0,若((p)= ((q),Epq(0,0)=Epq(1,1)=0;而((p) (((q),Epq(0,1)和Epq(1,0)总是正值。因此,Epq项是子模函数[12],即满足Epq(0,0)+Epq(1,1)(Epq(0,1)+Epq(1,0)。从而,能利用最大流算法计算能量函数如式(15)极小值。构造加权无向图G={V,ε}。使得图像I的每个像素x或者p对应图G的一个顶点。数据项Ex确定t-link边的权重(t为辅助端点s或t);正则项Epq确定n-link边的权重,具体构造规则如表 1所示。
| 表 1 图G构造规则 |
算法过程
Step 1:初始化轮廓C,根据式(7)标注像素;
Step 2:利用式(9)计算c1(x)和c2(x);
Step 3:对每个像素x∈Ω,根据表(1)构造图G;
Step 4:计算图最小割集Cε,划分顶点集为2个不相交的子集S和T。
若vx∈S,则γ(x)=1;若vx∈T,则γ(x)=0;
Step 5:基于新标注集,利用式(9)更新c1(x)和c2(x);
Step 6:迭代(3)(5),直至c1(x)和c2(x)固定不变或者能量最小化。
2.3 复杂度分析新方法的主要耗费时间是更新c1(x)和c2(x),虽然式(9)有4个离散卷积项ΣΩg(x-y)I(y),ΣΩg(x-y),ΣΩg(x-y)γ(y),ΣΩg(x-y)I(y)((y),但ΣΩg(x-y)I(y),ΣΩg(x-y)并不依赖于轮廓演化,算法迭代前仅计算一次,而在每次迭代中计算ΣΩg(x-y)γ(y),ΣΩg(x-y)I(y)γ(y)。另外,算法中图构造及最大流算法与文献[12]有相同的多项式时间复杂度。因此,新方法仍然能保持多项式阶的时间复杂度。
3 仿真实验及评价在实验中,不仅评价新方法分割灰度非匀质图像的效果,还使用合成图像和医学图像与传统的CV[3]算法及最近出现的算法LBF[4],LCV[5],LIF[6]作比较。所有的实验基于OpenCV和MatlabR2010b编程环境和酷睿双核2 GHz个人计算机。
图 1比较方法、CV算法和LCV算法的分割结果。CV算法无法正确分割灰度非匀质图像(图 1列b);LCV算法能分割“T”型图像(图 1列c上),但分割包含6个不同灰阶圆形物体的复杂结构图像时,陷入局部极值,无法收敛到物体边界(图 1列c下)。然而,方法能正确分割这两类图像(图 1列d)。
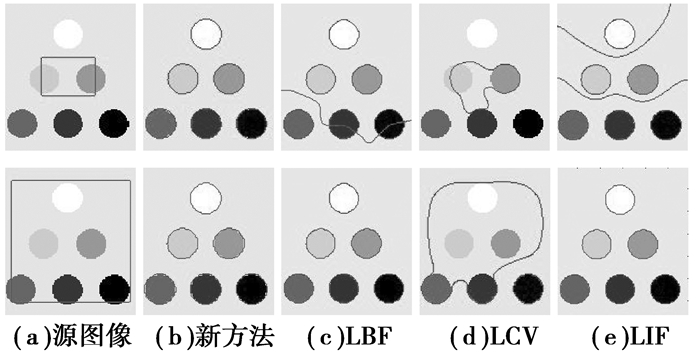
图 4是方法与LBF算法、LCV算法和LIF算法对合成多灰阶图像的分割结果。由该图可见,在不同初始轮廓线情况下,新方法都能精确检测出6个不同灰阶物体的边缘;LBF算法和LIF算法各分割正确一次,而LCV算法2次都分割失败。
|
图 4 不同算法对合成多灰阶图像的演化结果 |
图 5是新方法对2幅合成图像、2幅“Blood vessel”图像和1幅“T”型图像的分割过程及结果。第1行是包含有不同形状物体的合成图像,验证新方法的拓扑变化能力;第2行是包含6个不同灰阶圆形物体的合成图像;第3行和第4行“Blood vessel”图像具有部分非常弱的边缘,分割比较困难;第5行“T”型图像的背景是灰度非匀质的,且目标有“拐角”。图 5显示新方法对这几幅有挑战的图像都获得精确的分割结果。

|
图 5 新方法分割合成图像与真实图像的轮廓演化过程 |
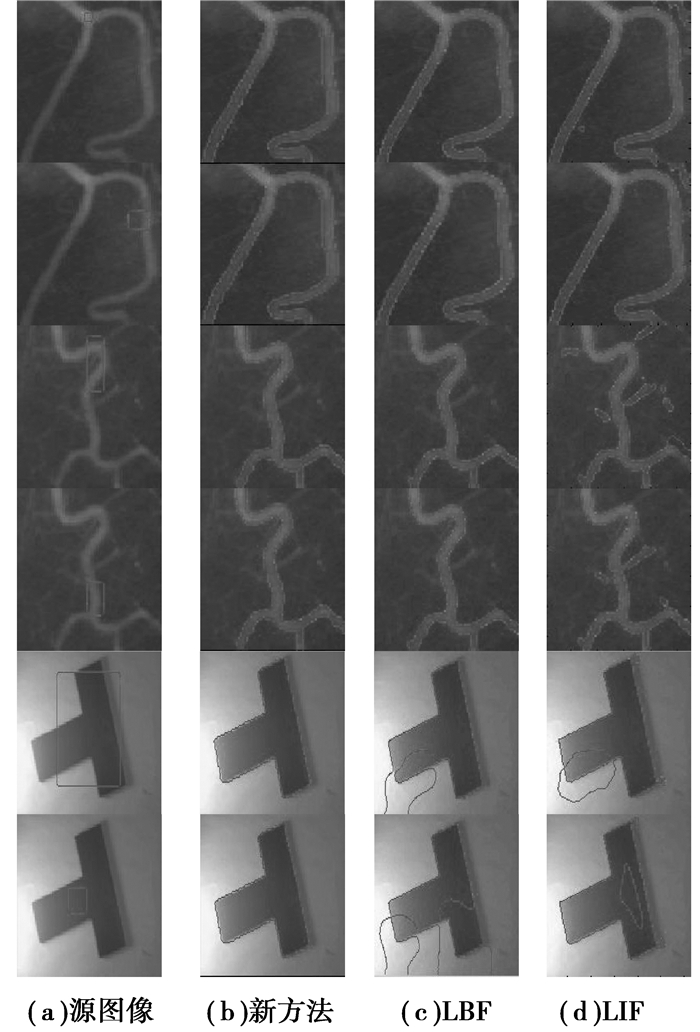
图 6比较新方法、LBF算法和LIF算法对不同模态图像的分割结果。从图中第一行到第4行可以看出,对不同初始化轮廓线的弱边缘“Blood vessel”图像,LBF算法都能有效分割,但LIF算法均无法精确定位目标边缘。在第5、6行,对“T”型图像分割时,当初始轮廓为小的正方形时(无足够的初始先验信息),LBF算法和LIF算法都不能收敛到物体边缘。然而,方法均获得精确分割结果。
|
图 6 研究方法与不同算法的分割结果比较 |
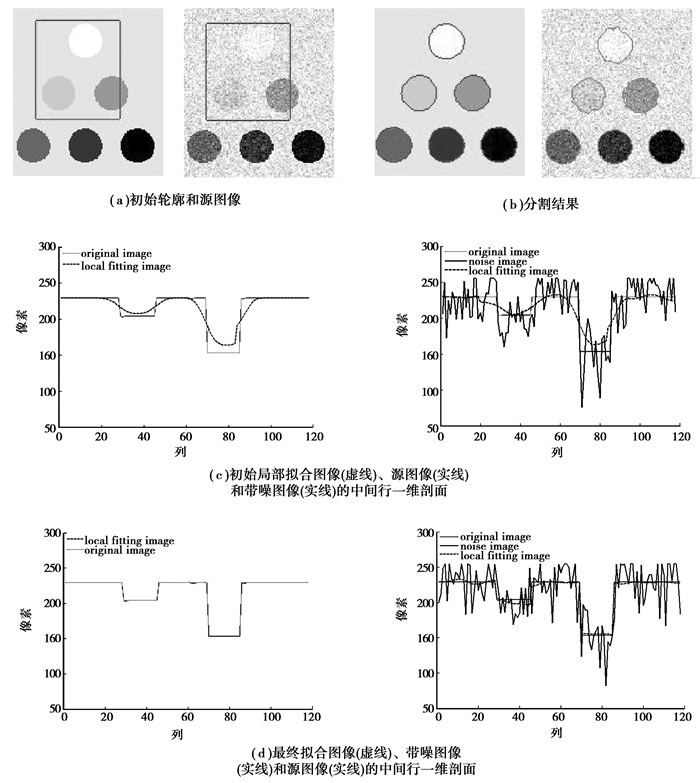
图 7是验证算法分割带加性高斯白噪声图像的效果。为清晰透视分割误差,画出局部拟合图像和源图像的一维剖面图(图 7列c,d)。行1是源图像,从分割结果及剖面可知,新方法能精确定位包含6个不同灰阶的圆形物体。行2是加零均值,标准差为0.01的带噪图像分割结果。从图像对比度来看,噪声是很高的。图 7行2显示,新方法能分割出被噪声污染的6个圆形物体,同时,局部拟合图像的一维剖面(图 7行2列d)也能看出仅有少量的被噪声影响的拟合偏差(分割结果表现为部分锯齿状边缘),这说明新方法对噪声是鲁棒的。
|
图 7 多灰阶图像及其带高斯噪声的分割结果 |
算法分割各类图像对应的参数,如表 2所示。从表 2中能够看出,对于弱边界的“Blood vessel”图像,适当增大尺度参数σ,从而减少对边缘信息的依赖。对边界明显的图像,如“T”型图像,要适当减小尺度参数σ,缩小局部范围,利于快速收敛到物体边界。对于参数λ1和λ1,为使演化曲线内外数据项公平竞争,一般设置为1,但对物体和背景灰度变化剧烈的图像,适当调整λ1和λ1,使之利于捕捉包含的不同灰阶物体。对于灰度缓慢变化的图像,适当减小正则项μ,可捕获图像的局部细节利于新轮廓的快速生成。
| 表 2 研究方法分割不同图像对应的参数 |
同时,对算法效率进行了量化评价,利用图 6的分割数据测试不同算法轮廓线演化的收敛迭代次数和计算时间,结果如表 3所示。从表 3可见,研究方法比其他方法有较快的演化效率。由于基于图的能量函数表示,能以大的步长演化,无论迭代次数,还是收敛时间都大大减少。
| 表 3 新方法与传统方法的速度比较 |
基于区域活动轮廓模型,提出一种快速有效的灰度非匀质图像分割方法。该方法结合局部区域信息和正则长度项约束演化轮廓收敛于物体边界。通过核函数定义局部连通结构,确定邻近点与其中心点的权重,能更有效表征图像的灰度非匀质分布特征。为避免计算代价高昂的水平集方法,在二维网格,利用割测度逼近正则长度项,并基于最大流算法求解能量函数极小值。大量实验表明新方法的有效性和较低的计算时间,同时,对初始轮廓线和噪声有一定的鲁棒性。在后续工作中,我们将研究更为复杂拓扑结构物体的分割,并应用于可视目标追踪。
| [1] | Ciesielski K C, Udupa J K. A framework for comparing different image segmentation methods and its use in studying equivalences between level set and fuzzy connectedness frameworks[J]. Computer Vision and Image Understanding, 2011, 115(6): 721–734. DOI:10.1016/j.cviu.2011.01.003 |
| [2] | Caselles V, Kimmel R, Sapiro G, et al. Geodesic active contours[J]. International Journal of Computer Vision, 1997, 22(1): 61–79. DOI:10.1023/A:1007979827043 |
| [3] | Chan T F, Vese L A. Active contours without edges[J]. IEEE Transactions on Image Processing, 2001, 10(2): 266–277. DOI:10.1109/83.902291 |
| [4] | Li C M, Kao C Y, Gore J C, et al. Minimization of region-scalable fitting energy for image segmentation[J]. IEEE Transactions on Image Processing, 2008, 17(10): 1940–1949. DOI:10.1109/TIP.2008.2002304 |
| [5] | Lankton S, Tannenbaum A. Localizing region-based active contours[J]. IEEE Transactions on Image Processing, 2008, 17(11): 2029–2039. DOI:10.1109/TIP.2008.2004611 |
| [6] | Zhang K H, Song H H, Zhang L. Active contours driven by local image fitting energy[J]. Pattern Recognition, 2010, 43(4): 1199–1206. DOI:10.1016/j.patcog.2009.10.010 |
| [7] |
王利, 陈允杰, 韦志辉, 等.
克服灰度不均匀性的脑MR图像分割模型[J]. 计算机辅助设计与图形学学报, 2009, 21(11): 1624–1631.
WANG Li, CHEN Yunjie, WEI Zhihui, et al. A novel model for brain MR images segmentation in the presence of intensity inhomogeneity[J]. Journal of Computer-Aided Design & Computer Graphics, 2009, 21(11): 1624–1631. (in Chinese) |
| [8] |
刘建磊, 冯大政.
一种全局最优的非匀质图像分割算法[J]. 西安电子科技大学学报:自然科学版, 2011, 38(2): 66–71.
LIU Jianlei, FENG Dazheng. Non-homogenous image segmentation with global optimization[J]. Journal of Xidian University, 2011, 38(2): 66–71. (in Chinese) |
| [9] | Liu S G, Peng Y L. A local region-based Chan-Vese model for image segmentation[J]. Pattern Recognition, 2012, 45(7): 2769–2779. DOI:10.1016/j.patcog.2011.11.019 |
| [10] | El-Zehiry N, Sahoo P, Elmaghraby A. Combinatorial optimization of the piecewise constant Mumford-Shah functional with application to scalar/vector valued and volumetric image segmentation[J]. Image and Vision Computing, 2011, 29(6): 365–381. DOI:10.1016/j.imavis.2010.09.002 |
| [11] | Kolmogorov V, Zabin R. What energy functions can be minimized via graph cuts[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(2): 147–159. DOI:10.1109/TPAMI.2004.1262177 |
| [12] | Boykov Y, Funka-Lea G. Graph cuts and efficient N-D image segmentation[J]. International Journal of Computer Vision, 2006, 70(2): 109–131. DOI:10.1007/s11263-006-7934-5 |
 2013, Vol. 36
2013, Vol. 36


