在图像处理中,图像修复是一项重要的基础性研究课题。数字图像修复是根据图像中残留的信息,自动地恢复图像中遗失或损坏的信息,使修复后的图像接近或达到原始图像的视觉效果。Bertalmio等首先提出了基于偏微分的图像修复算法[1],后来Rudin等将变分法思想引入到图像修复中[2],由于全变分(Total variation,TV)模型固有的缺点,即不满足人类视觉中的“连接性”准则,Chan等又在TV模型的基础上,引入曲率扩散项k,提出了曲率驱动扩散(Curvature driven diffusion,CDD)修复模型[3],让图像中不自然的大曲率迅速扩散,达到连接较大断裂部位的目的。
TV模型的修复时间较少,但它是趋向于生硬的最短直线连接,修复效果较差;CDD模型在TV模型的基础上引入了扩散引子曲率k,使得修复效果更自然。但CDD模型所花费的时间往往是TV模型的很多倍。最近几年有文献提出了基于CDD模型和TV模型的改进模型[7-8, 14-16]。文献[7]提出的基于CDD模型的快速修复方法,大大加快了CDD的修复速度,但由于它是基于领域平均的方法,而不是逐渐迭代修正的结果,所以修复效果不是很理想;文献[8]提出了一种基于p-laplace的CDD修复模型,提高了CDD的修复质量,由于不全是各向异性扩散,在一定程度上提高了CDD的速度,但由于该方法本身还是用CDD方法实现的,所以速度提高不明显。笔者提出一种基于CDD模型的自适应算法,引入曲率自适应系数q和梯度的自适应系数p,在图像修复时,只在较大曲率时使用CDD模型,有效减少修复时间。同时,只在较大梯度使用各向异性扩散,而平坦区域使用各向同性扩散,比全局使用各项异性扩散效果更优。实验表明该方法在图像修复的时间和效果上都得到了不同程度的提高。
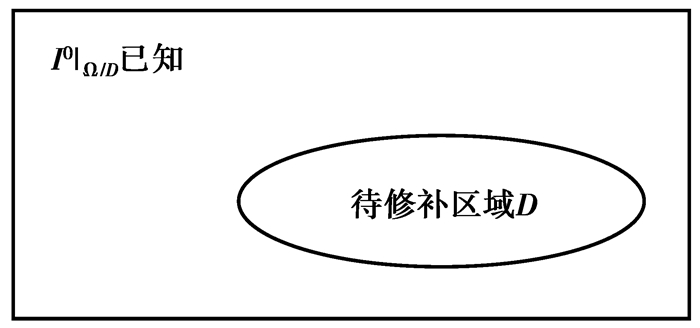
1 CDD模型CDD模型是建立在TV模型[4-6]的基础上的。在图像修复中,图像修补示意图如图 1所示。
|
图 1 图像修复示意图 |
D表示破损区域,Ω\D表示已知区域,常用的退化模型是
| $ I_{\mathit{\Omega \backslash D}}^0\left( x \right) = I{\left( x \right)_{\mathit{\Omega \backslash D}}} + n\left( x \right), $ | (1) |
在被污染的图像中,噪声图像一般满足加性关系,I(x)Ω\D表示原始的未破损图像,n(x)表示均值为0,方差为δ的高斯白噪声。TV模型在约束条件下的泛函极值为
| $ \min \left( J \right) = \int_\mathit{\Omega } {\left| {\nabla I} \right|{\rm{d}}x} + \frac{\lambda }{2}\int_{\mathit{\Omega \backslash D}} {{{\left| {I - {I^0}} \right|}^2}{\rm{d}}x} , $ | (2) |
其中,λ表示Lagrange乘子,根据变分原理,可求得与之对应的Euler-Largange方程为
| $ - {\rm{div}}\left[ {\frac{{\nabla I}}{{\left| {\nabla I} \right|}}} \right] + {\lambda _D}\left( x \right)\left( {I - {I^0}} \right) = 0, $ | (3) |
其中,
| $ {\lambda _D}\left( x \right) = \lambda \cdot {1_{\mathit{\Omega \backslash D}}} = \left\{ \begin{array}{l} \lambda ,x \in \mathit{\Omega /D},\\ 0,x \in D, \end{array} \right. $ | (4) |
由此可知,式(3)中的第一项是扩散项,扩散系数是
Chan等在TV模型的基础上,提出了CDD模型[3],即在式(3)中的扩散项中加入了另一个扩散系数,即曲率k。在大曲率的地方,让扩散加强,从而能够修复破损更大的图像,也就满足了“连接性”的原则。CDD模型Euler-Lagrange方程为
| $ - {\rm{div}}\left[ {\frac{{f\left( k \right) \cdot \nabla I}}{{\left| {\nabla I} \right|}}} \right] + {\lambda _D}\left( x \right)\left( {I - {I^0}} \right) = 0, $ | (5) |
可以看出,由于
由于图像基本上是接近平滑的变化,所以在曲率变化特别大的地方一定是破损区域,需要用到CDD模型加强扩散,而在其他地方使用TV模型;同时,在图像修复时要求强调边缘,如果在平坦区域,也使用各向异性扩散,不仅速度慢,而且可能造成虚假边缘,所以在平坦区域选择各向同性优于各向异性。所以根据这2个原则,引入了2个自适应参数:曲率自适应系数q和梯度自适应系数p。曲率自适应系数q由曲率k计算得出,在大曲率时,需要扩散加强,选择使用CDD修复,而在小曲率时只需要使用TV就能达到修复较好的目的,这样可以有效减少CDD模型的修复时间;梯度自适应系数p根据不同图像的变化程度给出(变化越强烈p越小,1<p<2),在大梯度时各项异性扩散,这样就能能有效保护边缘,而在小梯度时选择各项同性扩散,同时各向同性扩散还减少了在平坦区域使用TV模型所造成的阶梯效应,达到提高修复质量的目的。
2 基于CDD模型的自适应图像修复算法 2.1 CDD模型扩散系数的分析在CDD模型中,传导率
所以,选择
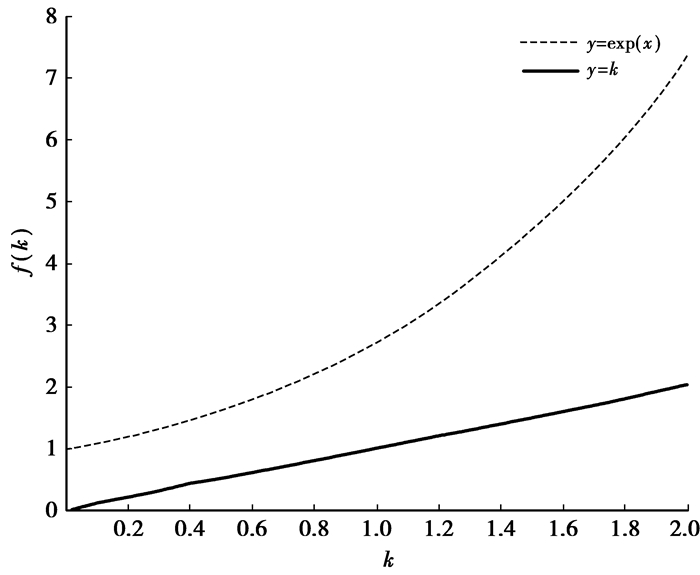
|
图 2 f(k)函数的比较 |
选择
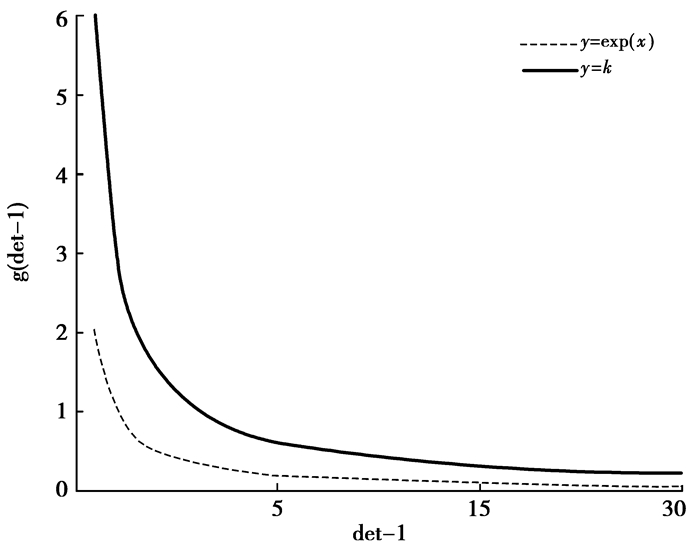
|
图 3 |
根据上述分析可知:大曲率时需扩散强,而CDD模型中的曲率因子能加强扩散,所以在大曲率时使用CDD模型较好;而小曲率的时候使用TV模型即可;在大梯度时,为了保护边缘使用TV模型较好;小梯度时,即平坦区域使用热扩散模型较好。因此,引入了根据曲率大小选择曲率扩散模型的自适应系数q和根据图像变化大小择扩散模型的自适应系数p。其Euler-Lagrange方程为
| $ - {\rm{div}}\left[ {\frac{{f{{\left( k \right)}^{2 - q}} \cdot \nabla I}}{{{{\left| {\nabla I} \right|}^{2 - p}}}}} \right] + {\lambda _D}\left( x \right)\left( {I - {I^0}} \right) = 0, $ | (6) |
其中,
| $ q = 1 + \frac{1}{{1 + {{\left| k \right|}^2}}}。$ | (7) |
由式(6)、(7)可知,1≤q≤2,1≤p≤2。q的取值与图像的曲率有关,在图像变化大处曲率k就大,当|k|2→∞时,q→1,即保留了曲率扩散项这一项;在图像变化不明显处曲率k小,当|k|2→0时,q→2,即曲率扩散项为0,此时就简化为TV模型。p的取值与图像的梯度有关,破损区图像边缘较多的话,p的取值越小,反之越大。
在不考虑噪声的情况下,用极限法来分析上面的自适应模型。p和q的极限值可以取1和2,那么,可以组合成4种不同的情况:
1) p=2,q=2时;表示曲率小,梯度小的平坦区域,修补模型为
| $ \frac{{\partial I}}{{\partial t}} = \Delta I, $ | (8) |
此为调和模型,即各项同性,适合于修复平坦区域,其修复效果优于各向异性扩散,同时,热扩散修补模型的扩散速度比较快。所以在这种区域,用该模型在速度和效果上都优于CDD模型。
2) p=2,q=1时;表示曲率小,梯度大的光滑边缘区域,修补模型为
| $ \frac{{\partial I}}{{\partial t}} = \nabla \left( {\frac{{\nabla I}}{{\left| {\nabla I} \right|}}} \right), $ | (9) |
即TV模型,是各项异性扩散,由于只在边缘处扩散,所以能很好的保护边缘。同时,由于曲率小,因此曲率对修复效果影响不大,所以略去计算曲率,大大减少了修复时间。在这种区域,修复速度优于CDD模型。
以上2个模型就是p-laplace算子扩散模型的2个特例[8-10],p-laplace算子实质上就是一个各项异性扩散的方程
| $ {\Delta _p}I = {\left| {\nabla I} \right|^{p - 2}}{I_{\xi \xi }} + \left( {p - 1} \right){\left| {\nabla I} \right|^{p - 2}}{I_{\eta \eta }}, $ | (10) |
扩散系数|▽I|p-2和((p-1)|▽I|p-2控制着该扩散方程的扩散行为,只要合理选择p值,就能达到某种扩散目的,以上是2种极限情况。
3) p=1,q=2时;表示曲率大,梯度小的图像变化较大的平坦区域,修补模型为
| $ \frac{{\partial I}}{{\partial t}} = \nabla \left( {f\left( k \right) \cdot \nabla I} \right), $ | (11) |
该模型就是廉晓丽等介绍的快速CDD(QCDD)修复模型[11]。QCDD直接建立在热扩散的基础上,此时扩散强度仅依赖于等照线的几何信息——曲率。由于曲率的引入,该模型满足“连接整体性准则”。由于QCDD模型建立在热扩散的基础上,去除了梯度值对扩散速度的负面影响,因此其修复速度必然会加快。
4) p=1,q=1时;表示曲率大,梯度大的变化强烈的边缘信息,修补模型为
| $ \frac{{\partial I}}{{\partial t}} = \nabla \left( {\frac{{f\left( k \right) \cdot \nabla I}}{{\left| {\nabla I} \right|}}} \right)。$ | (12) |
该模型就是CDD模型,虽然修复速度较慢,但在大曲率,大梯度时修复效果较好。
可以看出,上面的4个模型中有3个模型速度快于CDD模型,有一个修复效果优于CDD模型。只要选取适当的p、q值,修复模型能近似于以上四个模型,使修复效果更加,所以该自适应算法在修复质量和速度上都能得到提高。
3 数值实现修复过程是首先确定待修补的区域,然后利用式(6)模型的离散化方案修复。具体采用如下半点显式方案实现
| $ {I^{\left( {n + 1} \right)}} = {I^{\left( n \right)}} + \Delta t \cdot {\mathit{\boldsymbol{j}}^{\left( n \right)}}, $ | (13) |
其中矢量
| $ \nabla \cdot \mathit{\boldsymbol{j}} = \frac{{j_{\left( {d,0} \right)}^1 - j_{\left( { - d,0} \right)}^1}}{h} + \frac{{j_{\left( {0,d} \right)}^2 - j_{\left( {0, - d} \right)}^2}}{h}, $ | (14) |
其中d为网格长度,h为2个网格点之间的距离。半点方案时取d=1/2,h=1,如图 4所示。这时要求计算半点梯度▽I和半点曲率k。
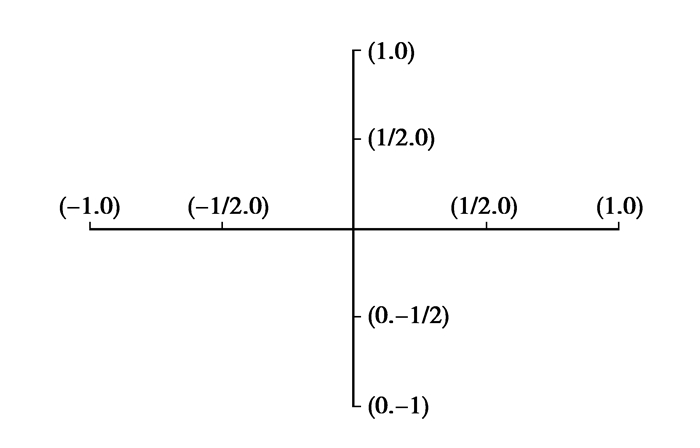
|
图 4 半点网络 |
半点梯度|▽I|,以求▽I(1/2,0)为例
| $ \begin{array}{l} \nabla {I_{\left( {1/2,0} \right)}} = \left( {\frac{{\partial I}}{{\partial x}}\left| {_{\left( {1/2,0} \right)}} \right.,\frac{{\partial I}}{{\partial y}}\left| {_{\left( {1/2,0} \right)}} \right.} \right) \approx \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left( {\frac{{I\left( {1,0} \right) - I\left( {0,0} \right)}}{1},\frac{{I\left( {1/2,1} \right) - I\left( {1/2, - 1} \right)}}{2}} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left( \begin{array}{l} \frac{{I\left( {1,0} \right) - I\left( {0,0} \right)}}{1},\\ \frac{{\left( {I\left( {0,1} \right) + I\left( {1,1} \right)} \right) - \left( {I\left( {0, - 1} \right) + I\left( {1, - 1} \right)} \right)}}{4} \end{array} \right) \end{array} $ | (15) |
半点曲率k,以求k(1/2,0)为例
| $ \begin{array}{*{20}{c}} {{k_{\left( {1/2,0} \right)}} = \nabla {{\left( {\frac{{\nabla I}}{{\left| {\nabla I} \right|}}} \right)}_{\left( {1/2,0} \right)}} = }\\ {\frac{\partial }{{\partial x}}{{\left[ {\frac{{{I_x}}}{{\left| {\nabla I} \right|}}} \right]}_{\left( {1/2,0} \right)}} + \frac{\partial }{{\partial y}}{{\left[ {\frac{{{I_y}}}{{\left| {\nabla I} \right|}}} \right]}_{\left( {1/2,0} \right)}},} \end{array} $ | (16) |
其中
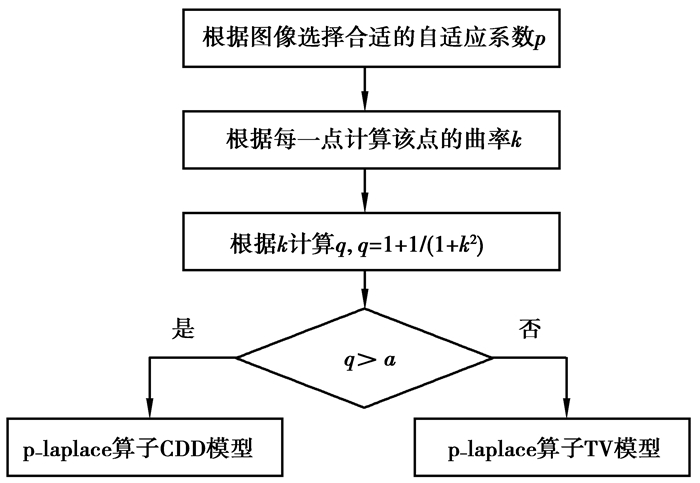
修复图像的过程如图 5所示。p是根据图像的平坦陡峭程度来选择的,图像变化越平缓,p越接近2,否则越接近1;a是曲率自适应系数的一个阈值,1<a<2,当图像破损处的大曲率比较多时,将阈值a的值提高。图 5表示,当q<a时,传导系数为
|
图 5 自适应图像修复算法流程图 |
在Matlab7.9.0上对TV、CDD、文献[7]、文献[8]和自适应CDD模型进行了仿真实验。自适应CDD模型中,Lena图像取p=1.5,a=1.55,K=0.8,文献[8]中取p=1.5;Cameraman图像取p=1.3,a=1.4,K=1.2,文献[8]中取p=1.3。用峰值信噪比(PSNR)来作为客观衡量的标准。
图 6是512×512大小的Lena图像,破损了5 719个像素点,图 7是256×256大小的Cameraman图像,破损了2 275个像素点。分别经过TV、CDD、文献[7],文献[8]和自适应CDD300次迭代和500次迭代后的结果。

|
图 6 Lena图像在5种修复模型下的结果 |

|
图 7 Cameraman图像在5种修复模型下的结果 |
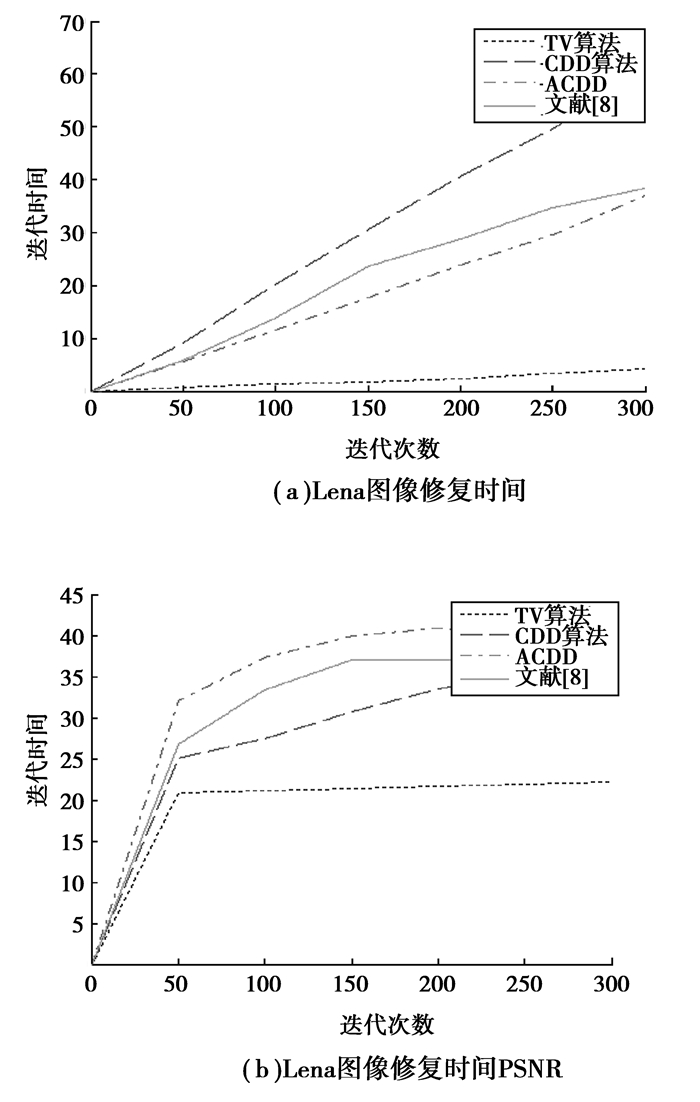
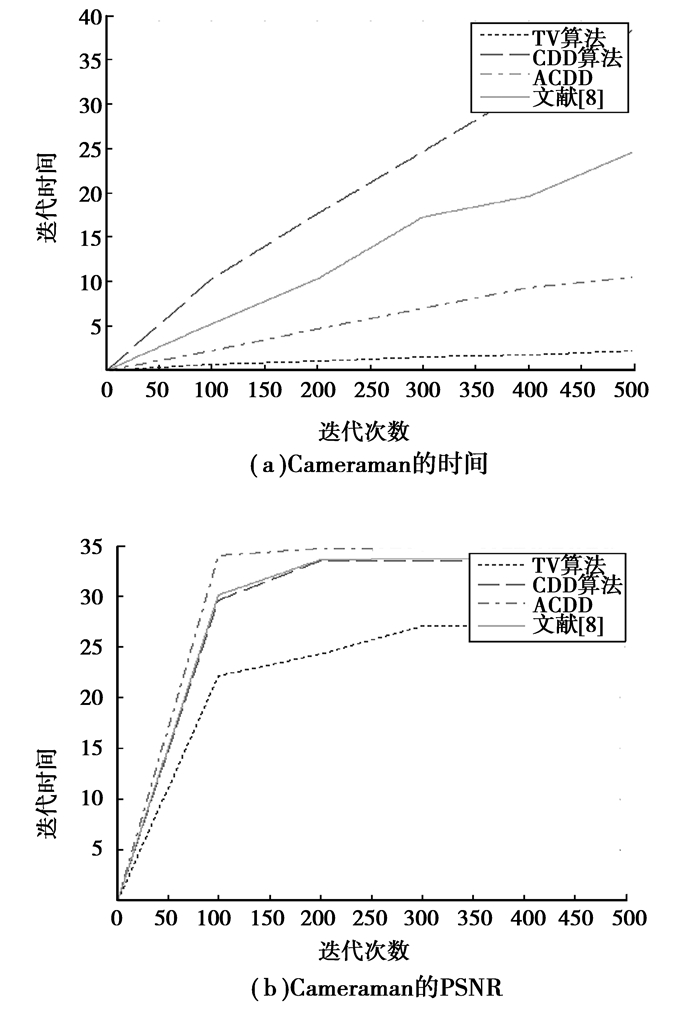
从图 6、7可以看出,TV算法在破损面积比较大和纹理丰富的地方不能修复;CDD算法虽然将大面积破损的地方有进行连接,但边缘处并没有被连接上;文献[7]的效果都比较差,主要是因为它的修复过程是基于领域平均的,一次就修复完成,不需要进行反复的迭代计算,所以速度非常快,但是由于它不是迭代的结果的,所以最初错误的修复不能在后面的迭代中得到修正,而是越变越大,特别是这2幅破损图像,破损的像素都比较宽,所以修复的质量很差,这种方法一般适用于破损面积不太大的图像;而文献[8]的修复质量比较好,是因为它也是基于CDD模型迭代修复的结果,所以质量较好,且由于p-laplace的原因,在有些地方各向同性扩散,有些地方各向异性扩散,而各向同性扩散的速度快,所以修复时间也有减少,但也正是由于它还是CDD模型的迭代,所以修复时间仍然比较长。而所提出的自适应CDD模型,在Lena图像中不仅修复了头发部分的破损,还将大面积破损的地方连接起来了,在Cameraman中腿破损的地方修复更接近原图像。通过以上2个实验发现,自适应CDD模型效果优于前面2个模型。下面再从修复时间和峰值信噪比评估算法的性能。各算法的修复时间与峰值信噪比如表 1和图 8、图 9所示。
| 表 1 算法的修复时间与峰值信噪比 |
|
图 8 Lena图像修复时间与PSNR曲线 |
|
图 9 Cameraman图像修复时间与PSNR曲线 |
从上面的结果看出,虽然文献[7]和TV算法在修复时间上有绝对优势,但效果往往不佳;文献[8]效果不错,但修复时间又太长,而自适应CDD模型折中了TV模型和CDD模型的速度,同时又提高了CDD模型的效果。所以自适应CDD模型综合性能优于其他模型。
5 结语在分析CDD模型和TV模型的基础上,提出了一种基于CDD模型的自适应图像修复算法,引入曲率自适应系数q和梯度的自适应系数p,在图像修复时,只在较大曲率时使用CDD模型,有效减少修复时间。同时,只在较大梯度使用各向异性扩散,而平坦区域使用各向同性扩散,比全局使用各项异性扩散效果更优。实验表明,该算法在时间和效果上都要优于CDD修复模型。
| [1] | Bertalmio M, Sapiro G, Caselles V, et al. Image inpainting[C]. Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques, July 23-28, 2000, New Orleans, Louisiana, USA. New York:ACM, 2000, 1:417-424. |
| [2] | Rudin L I, Osher S, Fatemi E. Nonlinear total variation based noise removal algorithms[J]. Physics D, 1992, 60(1/2/3/4): 259–268. |
| [3] | Chan T F, Shen J. Non-texture inpainting by curvature-driven diffusions (CDD)[J]. Journal of Visual Communication and Image Representation, 2001, 12(4): 436–496. DOI:10.1006/jvci.2001.0487 |
| [4] | Chan T F, Shen J. Mathematical models for local non-texture inpainting[J]. SIAM Journal of Applied Mathematics, 2002, 62(3): 1019–1043. DOI:10.1137/S0036139900368844 |
| [5] | Chan T F, Kang S H, Shen J H. Euler's elastica and curvature-based inpainting[J]. SIAM Journal on Applied Mathematics, 2003, 63(2): 564–592. DOI:10.1137/S0036139901390088 |
| [6] | Esedoglu S, Shen J H. Digital inpainting based on the Mumford-Shah-Euler image model[J]. European Journal of Applied Mathematics, 2002, 13(4): 353–370. |
| [7] | Qu L W, Liang S, Wang D N. A fast inpainting model based on curvature-driven diffusions[J]. Chinese Journal of Electronics, 2007, 16(4): 644–647. |
| [8] | Li S L, Wang H Q. Image inpainting using curvature-driven diffusions based on p-laplace operator[C]//Proceedings of the 20094th International Conference on Innovative Computing, Information and Control, December 7-9, 2009, Kaohsiung, Taiwan, China. Piscataway:IEEE Press, 2009, 12:323-325. |
| [9] |
祝轩, 周明全, 耿国华, 等.
曲率驱动与边缘停止相结合的非纹理图像修复[J]. 计算机科学, 2008, 35(12): 212–213, 238.
ZHU Xuan, ZHOU Mingquan, GEN Guohua, et al. Non-texture inpainting by combination of the curvature-driven and edge-stopping nonlinear diffusion[J]. Computer Science, 2008, 35(12): 212–213, 238. DOI:10.3969/j.issn.1002-137X.2008.12.057 (in Chinese) |
| [10] |
张红英, 彭启琮, 吴亚东.
数字破损图像的非线性各向异性扩散修补算法[J]. 计算机辅助设计与图形学学报, 2006, 18(10): 1541–1546.
ZHANG Hongying, PENG Qicong, WU Yadong. Digital image inpainting algorithm for damaged images based on nonlinear anisotropic diffusion[J]. Journal of Computer-Aided Design & Computer Graphics, 2006, 18(10): 1541–1546. DOI:10.3321/j.issn:1003-9775.2006.10.014 (in Chinese) |
| [11] |
张红英, 彭启琮.
数字图像修复技术综述[J]. 中国图象图形学报, 2007, 12(1): 1–10.
ZHANG Hongying, PENG Qicong. A survey on digital image inpainting[J]. Journal of Image and Graphics, 2007, 12(1): 1–10. DOI:10.11834/jig.20070102 (in Chinese) |
| [12] |
张红英, 彭启琮.
全变分自适应图像去噪模型[J]. 光电工程, 2006, 33(3): 50–53.
ZHANG Hongying, PENG Qicong. Adaptive image denoising model based on total variation[J]. Opto-Electronic Engineering, 2006, 33(3): 50–53. (in Chinese) |
| [13] |
廉晓丽, 徐中宇, 冯丽丽, 等.
一种新的基于偏微分方程的图像修复[J]. 计算机工程, 2009, 35(6): 234–236.
LIAN Xiaoli, XU Zhongyu, FENG Lili, et al. Novel image inpainting based on partial differential equation[J]. Computer Engineering, 2009, 35(6): 234–236. (in Chinese) |
| [14] |
赵颜伟, 李象霖.
基于CDD模型的快速图像修复算法[J]. 计算机仿真, 2008, 25(10): 223–227.
ZHAO Yanwei, LI Xianglin. A rapid image inpainting algorithm based on CDD model[J]. Computer Simulation, 2008, 25(10): 223–227. DOI:10.3969/j.issn.1006-9348.2008.10.057 (in Chinese) |
| [15] |
赵颜伟, 李象霖.
一种基于TV模型的快速图像修复算法[J]. 微电子学与计算机, 2009, 26(6): 253–256, 260.
ZHAO Yanwei, LI Xianglin. A rapid image inpainting algorithm based on TV model[J]. Microelectronics & Computer, 2009, 26(6): 253–256, 260. (in Chinese) |
| [16] |
檀结庆, 汪忠庆.
一种新的基于邻近像素点的图像修复算法[J]. 合肥工业大学学报:自然科学版, 2009, 29(9): 1072–1076.
TAN Jieqing, WANG Zhongqing. A novel image inpainting algorithm based on adjacent pixels[J]. Journal of Hefei University of Technology:Natural Science, 2009, 29(9): 1072–1076. (in Chinese) |
 2013, Vol. 36
2013, Vol. 36


