图像匹配技术是目标定位最基本也是最常用的方法。在许多图像测量系统中,目标的精确定位是个关键问题,例如有时需要把在不同时间,不同成像条件下对同一目标获取的2幅或者多幅图像进行比较对准,另外,根据已知的模板到另一幅图中找到相应的模板,这就需要用到图像的匹配。图像匹配就是将模板图与参考图进行比较匹配,并用一个计算结果量化其相似程度。如果运算结果显示参考图与模板图相同或相关性最大,则认为图像匹配成功。因此图像匹配问题可以归结为“相关性”度量的问题。相关性的大小衡量图像的匹配程度:若相关性大,则说明2幅图像的匹配程度高;反之,则匹配程度小或者无匹配关系。图像匹配主要可分为以灰度为基础的匹配和以特征点为基础的匹配[1-2]。基于特征点的匹配法要求能可靠地提取图像中有效的特征点,并能克服由部分遮挡带来的特征缺失及边界问题的鲁棒性。基于灰度的图像匹配方法主要是根据统计学原理以计算图像的灰度相关性为基础,此方法对光线的变化和局部噪声比较敏感,并且匹配精度不高。归一化的相关法被证明是一种可靠的模式匹配技术[3-4],相关表面的亚像素的定位精度可以通过插值来获得。分形因具有自相似的重要特征,所以在充分利用图像相关性方面独具潜力,它还能抗面内角度旋转。所以提出了基于分形维数的亚像素级图像定位匹配法,提高匹配的准确度和精度。
1 分形维数的计算-最优盒计数法分形维数是分形几何描述分形特征的基本参数,因此它是本文图像匹配算法的基础。计算分形维数的方法有多种,如像素点覆盖法[5],毯子法[6],差分盒计数法[6]等。采用的是提出的分形维数计算方法——最优盒计数法[7],由于该方法能克服差分盒计数法中存在“空盒子”的缺陷,使计算的分形维数更准确。该方法采用差分盒计数法的划分方式对平面网格进行划分,具体实现步骤如下:
1) 将图像划分为r×r大小的网格,计算每个网格对应图像灰度曲面上的点集Zij={f1,f2,f3,…,fK}。
2) 对集合Zij中的每个元素fi进行si=fix(fi/r)+1操作,得到其所在盒子位置的集合S={s1,s2,s3,…,sk}。
3) 统计S中只出现一次的元素个数,确定覆盖整个分形图像所需盒子的总数。
4) 变换不同的尺寸r,同理计算所需的盒子总数,再用最小二乘法拟合得到的斜率就是分形维数。
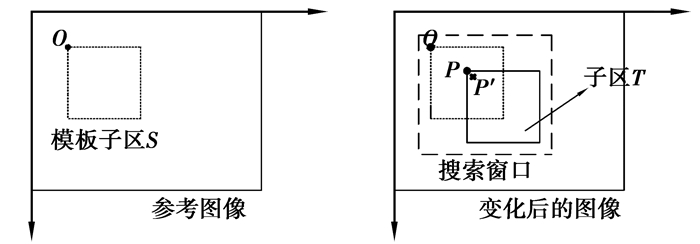
2 基于分形维数的亚像素图像定位匹配 2.1 基于分形维数的整像素点定位匹配应用基于分形理论的图像匹配技术将匹配点定位在像素级。基本思想[8-9]:在变化前的参考图像中选定一个感兴趣的子区S,再在变化后的参考图像中任意选定与子区S大小和形状都相同的子区T。将子区S分解成个次级子区,并使,用新的维数计算法分别计算出每个的分形维数。同理,以同样的方式将T子区分解成个次子区,使,并计算出每个次子区的分形维数。根据数学统计学的相关性原理,子区S与子区T之间的相关系数
| $ \rho = \frac{{\sum\limits_{i = 1}^n {\left( {{d_{{s_i}}} - {{\bar d}_s}} \right)\left( {{d_{{T_i}}} - {{\bar d}_T}} \right)} }}{{{{\left[{\sum\limits_{i = 1}^n {{{\left( {{d_{{s_i}}}-{{\bar d}_s}} \right)}^2}} } \right]}^{1/2}}{{\left[{\sum\limits_{i = 1}^n {{{\left( {{d_{{T_i}}}-{{\bar d}_t}} \right)}^2}} } \right]}^{1/2}}}}, $ | (1) |
其中,dS、dT分别为dSi、dTi的均值。如图 2,ρ等于1或者最大且接近1时找到子区起始点O的匹配点P,以确定像素级的匹配区域图T(即模板S与T匹配)。通常,在图像测量系统中,图像移动的未必是整像素位移。而利用式(1)来进行相关搜索匹配时模板只能以整像素为单位移动,所以搜索得到的子区T的起始位置(P)坐标只能是像素的整数倍。还需要通过其他方法来提高亚像素位移定位精度,获得子区T的较准确的起始位置坐标(假设P′),从而找到与子区S能准确匹配的子区。为了减少搜索时间,可以根据先验知识和经验来确定搜索窗口,让模板在此窗口范围内移动。
|
图 1 图像匹配示意图 |
|
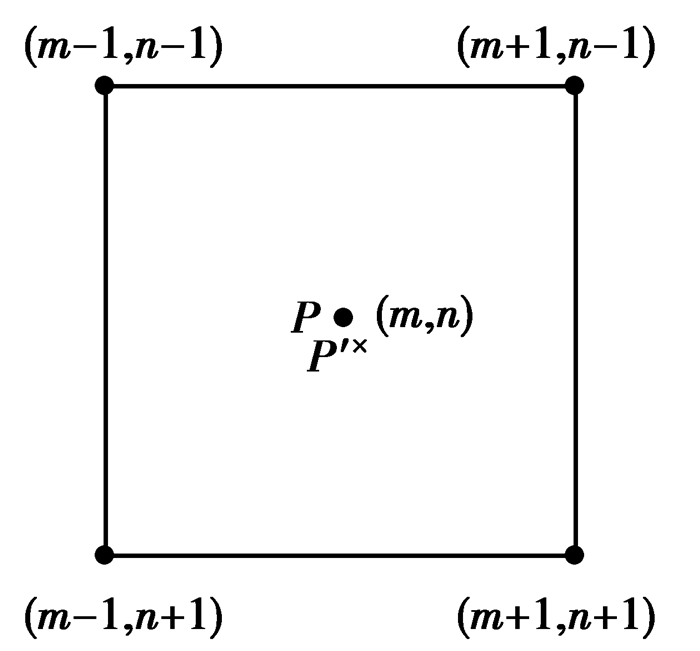
图 2 插值示意图 |
利用分形维数相关性只能得到整像素的匹配点,要得到亚像素的匹配点需要用插值法来实现。根据分形性质,图像的分形维数与它实际的分形数值一样,并且在不同的变换比率下仍保持不变[8],所以可以利用分形插值法来实现亚像素定位。
插值示意图如图 2所示。
在图 2中,需要从子区S中的坐标O点得到变化后的子区T中的坐标P′点,但是映射得到的这个坐标P′点并没有位于图像中的整数坐标上,而是映射到了以P为中心的4个像素坐标(m-1,n-1)、(m+1,n-1)、(m-1,n+1)、(m+1,n+1)所围成的矩形之间,其中,m,n都是整数坐标。现在的问题是如何根据这4个点的坐标值和灰度值求出与O灰度值相等的亚像素坐标点(P′)。这就需要用到分形插值将匹配点定位在亚像素级(如果求出的点有多个就对这些点求均值,均值就为所求亚像素级匹配点),再由亚像素匹配点找到亚像素级匹配区域。
分形插值曲面的思想[10-12]:令M=[a, b],N=[c, d];设D=M×N={(x,y):a≤x≤b,c≤y≤d},以Δx,Δy为步长,将D分为网格
| $ a = {x_0} < {x_1} < \cdots < {x_N} = b, $ | (2) |
给定一组数据点(xi,xj,zij),i=0,1,…,N,j=0,1,…,M。欲构造二元分形插值函数f:D→R,且有:f(xi,yj)=zij,i=0,1,…,N,j=0,1,…,M。令x方向的压缩变换为
| $ {\varphi _{\rm{n}}}\left( x \right) = {a_{\rm{n}}}x + {b_{\rm{n}}}, $ | (3) |
y方向的压缩变换为
| $ {\psi _{\rm{m}}}\left( y \right) = {c_{\rm{m}}}x + {d_{\rm{m}}}, $ | (4) |
且满足条件φn(x0)=xn-1,φn(xN)=xn,ψm(y0)=ym-1,ψm(yM)=ym,然后可有
| $ \begin{array}{l} {a_{\rm{n}}} = \left( {{x_{\rm{n}}} - {x_{{\rm{n}} - 1}}} \right)/\left( {{x_N} - {x_0}} \right), \\ {b_{\rm{n}}} = \left( {{x_{{\rm{n}} - {\rm{1}}}}{x_N} - {x_{\rm{n}}}{x_0}} \right)/\left( {{x_N} - {x_0}} \right), \\ {c_{\rm{m}}} = \left( {{y_{\rm{m}}} - {y_{{\rm{m}} - 1}}} \right)/\left( {{y_M} - {y_0}} \right), \\ {d_{\rm{m}}} = \left( {{y_{{\rm{m}} - {\rm{1}}}}{y_M} - {y_{\rm{m}}}{y_0}} \right)/\left( {{y_M} - {y_0}} \right)。\end{array} $ | (5) |
又令z方向的压缩变换为
| $ \begin{array}{l} {F_{ij}}\left( {x, y, z} \right) = {e_{ij}}x + {f_{ij}}y + {g_{ij}}xy + {a_{ij}}z + {k_{ij}}, \\ \;\;\;\;\;\left( {i \in \left\{ {1, 2, \cdots, N} \right\}, j \in \left\{ {1, 2, \cdots, M} \right\}} \right)。\end{array} $ | (6) |
式中,αij为分形插值曲面分形维数的自由参数,0≤αij<1,称为垂直比例因子。由式(4)可得
| $ \left\{ \begin{array}{l} {e_{ij}} = \left[{{z_{i-1, j-1}}-{z_{i, j - 1}} - {\alpha _{ij}}\left( {{z_{0, 0}} - {z_{N, 0}}} \right) - } \right.\\ \;\;\;\;\;\;\;\;\left. {{g_{ij}}\left( {{x_0}{y_0} - {x_N}{y_0}} \right)} \right]/\left( {{x_0} - {x_N}} \right);\\ {f_{ij}} = \left[{{z_{i-1, j-1}}-{z_{i - 1, j}} - {\alpha _{ij}}\left( {{z_{0, 0}} - {z_{0, M}}} \right) - } \right.\\ \;\;\;\;\;\;\;\;\left. {{g_{ij}}\left( {{x_0}{y_0} - {x_0}{y_M}} \right)} \right]/\left( {{y_0} - {y_M}} \right);\\ {g_{ij}} = \left[{{z_{i-1, j-1}}-{z_{i - 1, j}} - {z_{i, j - 1}} + {z_{ij}} - } \right.\\ \;\;\;\;\;\;\;\;\left. {{\alpha _{ij}}\left( {{z_{0, 0}} - {z_{N, 0}} - {z_{0, M}} + {z_{N, M}}} \right)} \right]/\\ \;\;\;\;\;\;\;\;\left( {{x_0}{y_0} - {x_N}{y_0} - {x_0}{y_M} + {x_N}{y_M}} \right);\\ {k_{ij}} = {z_{ij}} - {e_{i - 1.j}}{x_N} - {f_{ij}}{y_M} - {\alpha _{ij}}{z_N}{y_M}。\end{array} \right. $ | (7) |
令Wij(x,y,z)=(φi(x),ψj(y),Fij(x,y,z)),
| $ \left( {i = 1, 2, \cdots, N, j = 1, 2, \cdots, M} \right), $ | (8) |
则定义一个迭代函数系(IFS),Fij(x,y,z)为分形插值函数f的隐函数。
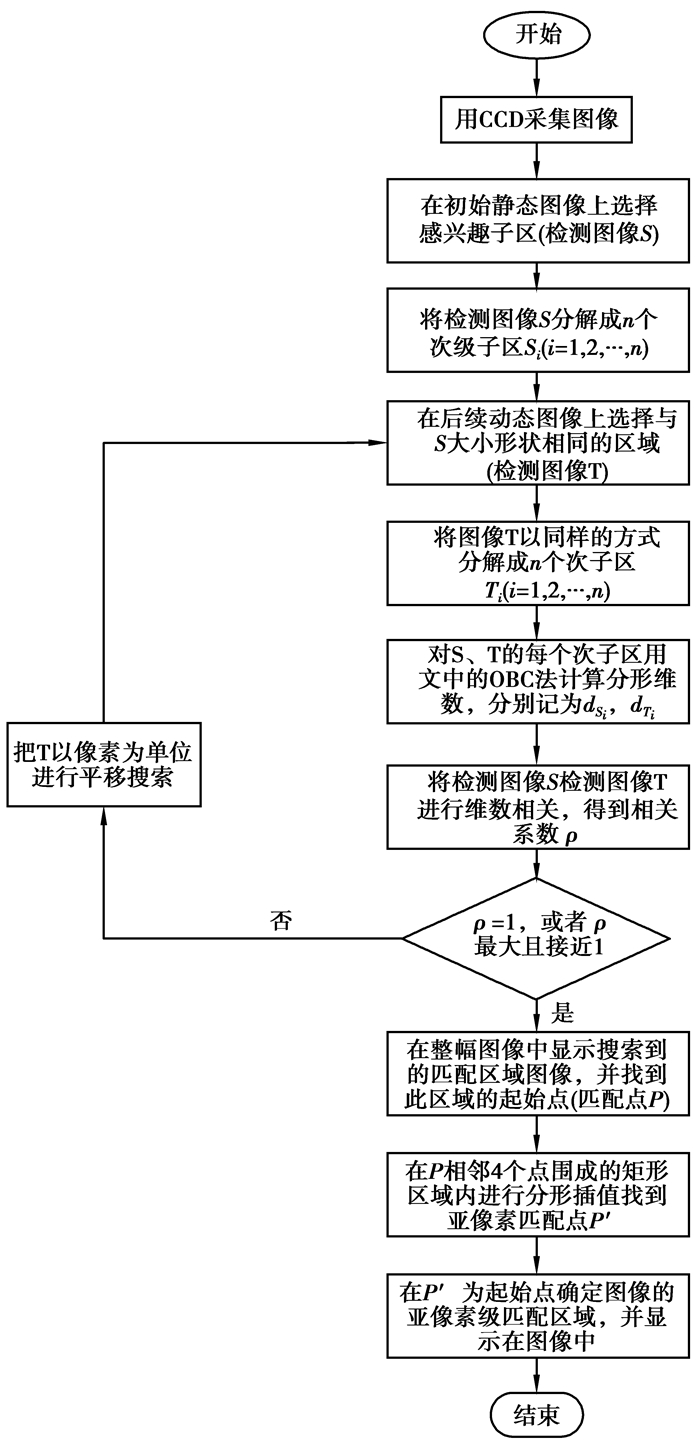
3 实验及结果分析根据上述的理论分析,要把模板图在经亚像素级移动后的图像中进行匹配,需要先运用分形维数相关性将匹配点定位在整像素级,然后对得到的整像素匹配点进行分形插值得到亚像素级的匹配点,从而在变化后的图像中较准确找到与模板图相匹配的区域图。整个过程的流程图如3所示。
|
图 3 图像匹配流程图 |
将图 4(a)作为原图,以(147,136)为起点选择64×64大小的子区作为匹配模板,再将原图经旋转后的图像作为待匹配图像,然后用提出的匹配法与基于灰度的相关匹配法[13-14]以及文献[15]中的匹配法进行实验比较,在待匹配图中找到与模板相匹配的区域和该区域的起始点,3种方法得到的匹配图的起始位置见表 1。

|
图 4 整像素移动图像匹配图 |
| 表 1 各种匹配结果比较表 |
从上表可以看出前2种方法对角度的旋转比较敏感,而基于分形维数的图像匹配对角度不敏感,旋转较小的角度还是能很好的匹配出来,所以将此方法用于图像的匹配具有很好的可行性。下面将用此方法进行图像的亚像素级位移的定位匹配。在图 4中,原图(a)是用搭建的机器视觉实验平台的MV-VD500SM相机采集的一块单片机芯片图,将以这个图为原图对提出的方法进行实验验证。在原图中以任意一点为起始点选择模板匹配图,然后将原图向右任意移动整数像素,再用研究方法在移动后的图像中找到与模板相同的子区。下面将以点(142,163)为例,以此点为起点选择一个大小为64×64的子区作为模板匹配图,再将原图水平移动5个像素,垂直移动6个像素,得到图(c),然后再研究方法得到匹配点是(147,169),最后找到与图(b)相匹配的子区。如图(d)所示,红色矩形框就是要找的匹配区域。任取8个点,然后以此点为起始点截取64×64大小子区(可选)为模板图,然与移动任意像素位移后的图像匹配,得到的匹配点如表 2,再另选采集的MEMS图像(e)为原图进行同样的实验,得到结果见表 3。
| 表 2 图 4(a)的整像素匹配结果 |
| 表 3 图 4(e)整像素匹配结果 |
从以上2表可以看出,提出的基于分形维数的图像匹配方法是有效的,匹配效果很好,整像素位移移动后的匹配误差都为0,匹配准确度很高。
在原图中任选一点为起始点坐标,并将原图向左移动非整像素位移,然后用研究方法进行匹配找到匹配区域。采用图 4(a)作为原图,以(147,136)为起点选择64×64的匹配模板,原图移动(5.1731,8.4562)后如图 5(a),整像素匹配点坐标为(142,128),经3次分形插值方法插出的曲面如图 5(b),视倾角为30°,视方位角为320°,亚像素级匹配点坐标为(141.75,127.5),最后得到的匹配图如图 5(c)。任选多组起始点,选择与上同样大小的模板子区,任意移动位移,所得匹配点结果见表 4,再用图 4(e)图为原图进行同样的实验,得到的实验结果见表 5。

|
图 5 亚像素移动的图像匹配过程图 |
| 表 4 图(a)的亚像素匹配结果 |
| 表 5 5图(e)的亚像素匹配结果 |
前面已经证明了基于分形维数图像匹配的有效性,表 4和表 5是以不同的图像为原图并选取多组亚像素平移数据,先用此方法将图像匹配到整像素位置,然后再用分形插值法将匹配点精确到亚像素级,从而较准确的定位匹配点,在变化后的图像中准确找到与模板相匹配的子区,实现图像的准确匹配。从表 4和5中的数据可以看出此方法能实现图像的亚像素匹配,匹配效果良好。
4 结论提出了一种基于分形维数的亚像素级图像定位匹配算法,分形理论在图像相关性方面具有优越性,还能抗图像的旋转。该算法以分形理论中的分形维数为基础,用维数相关性进行图像的整像素匹配,再用分形插值法将匹配定位在亚像素级,实现非整像素移动图像的精确匹配。
| [1] | Zong L, Wu Y H. A parallel matching algorithm based on image gray scale[C]//Proceedings of the 2009 International Joint Conference on Computational Sciences and Optimization, April 24-26, 2009, Sanya, Hainan, China. Piscataway:IEEE Press, 2009, 1:109-111 |
| [2] | Liu D H, Sun X Y, Feng L Q, et al. Intelligent pan-tilt control system of two cameras based on gray-scale image matching[C]//Proceedings of the 2007 International Conference on Machine Learning and Cybernetics, August 19-22, 2007, Hong Kong, China. Piscataway:IEEE Press, 2007, 1:454-458 |
| [3] |
韩冰, 王永明.
基于一种快速归一化积相关算法的图像匹配研究[J]. 兵工学报, 2010(2): 160–165.
HAN Bing, WANG Yongming. Research of image matching based on a fast normalized cross correlation algorithm[J]. Acta Armamentarii, 2010(2): 160–165. (in Chinese) |
| [4] | Luo J, Konofagou E. A fast normalized cross-correlation calculation method for motion estimation[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2010, 57(6): 1347–1357. DOI:10.1109/TUFFC.2010.1554 |
| [5] | 林道云. 掺用沸石岩矿粉建筑砂浆的力学性能及其抗压断面的分形定量表征[D]. 广州: 华南理工大学硕士学位论文, 2010. |
| [6] | 赵玲. 基于图像的多孔材料特征分析与物性测量研究[D]. 武汉: 武汉理工大学硕士学位论文, 2010. |
| [7] |
罗元, 蒋秋照, 张毅.
一种用于MEMS动态测量的最优盒计数分形维数算法[J]. 重庆邮电大学学报:自然科学版, 2012, 24(2): 231–235.
LUO Yuan, JIANG Qiuzhao, ZHANG Yi. A novel optimal box counting fractal dimension algorithm for MEMS dynamic measurement[J]. Journal of Chongqing University of Posts and Telecommunications:Natural Sciences Edition, 2012, 24(2): 231–235. (in Chinese) |
| [8] |
曾丽梅, 曹益平.
采用多特征窗口识别的散斑位移测量新方法[J]. 中国激光, 2009, 36(4): 949–953.
ZENG Limei, CAO Yiping. New method of displacement measurement based on laser speckle using multi-characteristic windows[J]. Chinese Journal of Lasers, 2009, 36(4): 949–953. (in Chinese) |
| [9] |
潘兵, 吴大方.
基于带通滤波成像的高温数字图像相关方法[J]. 光学学报, 2011, 31(2): 51–58.
PAN Bing, WU Dafang. High-temperature digital image correlation method based on optical band-pass filtering imaging[J]. Acta Optica Sinica, 2011, 31(2): 51–58. (in Chinese) |
| [10] |
姜文华, 于新瑞, 王石刚.
一种基于分形插值的复杂图像的亚像素算法[J]. 计算机应用与软件, 2005, 2(22): 85–87.
JIANG Wenhua, YU Xinrui, WANG Shigang. A subpixel algorithm of complex image based on fractal interpolation[J]. Computer Application and Software, 2005, 2(22): 85–87. (in Chinese) |
| [11] | Bouboulis P, Dalla L. Fractal interpolation surfaces derived from fractal interpolation functions[J]. Journal of Mathematical Analysis and Application, 2007, 336(2): 919–936. DOI:10.1016/j.jmaa.2007.01.112 |
| [12] | Bouboulis P, Dalla L. Closed fractal interpolation surfaces[J]. Journal of Mathematical Analysis and Applications, 2007, 327(1): 116–126. DOI:10.1016/j.jmaa.2006.04.009 |
| [13] |
刘莹, 曹剑中, 许朝晖, 等.
基于灰度相关的图像匹配算法的改进[J]. 应用光学, 2007, 28(5): 536–540.
LIU Ying, CAO Jianzhong, XU Chaohui, et al. Improvement of image matching algorithm based on gray correlation[J]. Journal of Applied Optics, 2007, 28(5): 536–540. (in Chinese) |
| [14] |
雷鸣, 张广军.
基于互相关的图像匹配亚像素定位[J]. 光电工程, 2008, 35(5): 108–113.
LEI Ming, ZHANG Guangjun. Image orientation algorithm with subpixel accuracy based on correlative matching method[J]. Opto-Electronic Engineering, 2008, 35(5): 108–113. (in Chinese) |
| [15] |
杨志云, 郝红卫, 陈骥.
一种精确而快速的块匹配算法[J]. 计算机工程, 2008, 34(2): 223–225.
YANG Zhiyun, HAO Hongwei, CHEN Ji. Accurate and fast block matching algorithm[J]. Computer Engineering, 2008, 34(2): 223–225. (in Chinese) |
 2013, Vol. 36
2013, Vol. 36


