为了更好地控制爆炸的破坏程度，有效地防止各种建筑物和构筑物遭受严重破坏，保证人们生命安全，最大限度地降低财产损失，需要充分研究爆炸机理，考虑爆炸所处的介质环境。由于爆炸作用的特殊性，实地测量和试验模型都具有一定局限性，有限元仿真模拟分析成了解决此问题的重要方法。李忠献等^[]1-3采用有限元、无穷元和杆件体系建立了地下衬砌及周围有限土区、远场无限土区以及基底滑移隔震大跨结构的计算模型，对由地下隧道内发生意外爆炸引起的地下爆炸波作用下基底滑移隔震动力响应进行了全面的分析。罗昆生等^[4]为研究炸弹在地面爆炸时对地铁区间隧道的影响，应用LS-DYNA软件分析了在地铁上方不同当量装药爆炸时地铁区间隧道的动力响应，得到了不同情况下地铁区间隧道的位移、速度及应变时程曲线，并进行了地面爆炸时地铁区间的安全评估。国胜兵等^[5]考虑竖向和水平向爆炸地震波对地下结构的耦合效应，基于有效应力动力分析方法，运用二维显式有限差分程序FLAC对地下结构在竖向和水平向爆炸地震波作用下的动力响应进行数值分析。Daniel等^[6]在考虑土介质与结构的弹塑性，采用有限元DYNA3D对由回填土、隔振材料、埋置炸药和部分埋置结构组成的土-结构体系进行了地下爆炸冲击作用下的动力相互作用分析。杜修力等^[7]基于显式有限元计算程序LS-DYNA3D和粘弹性人工边界条件，建立了爆腔-地下结构-软回填隔振层-岩土介质系统三维粘弹塑性动力响应分析模型，进行炸药爆炸作用下地下结构的动力响应分析，进一步讨论了软回填层的隔振效果。田力等^[8]针对双线地铁隧道中单侧隧道内爆炸引起的附近地面建筑物的动力响应及滑移隔振效应，采用将包含隧道的有限土区和地面多层建筑耦合而成相互作用的整体模型进行了数值模拟研究，并利用八结点等参单元和集中质量体系模拟了包含隧道有限土区和地面的多层建筑。刘建民等^[9]利用有限元软件ANSYNS/LS-DYNA对炸药地面爆炸或侵入土中浅层爆炸2种情形下埋地管道的动力响应问题作了三维模拟，并分析了炸药设置方式、炸药用量、爆心距和管道管径等因素对埋地管道损伤的作用。Syrunin等^[10]针对各种材料的圆柱型、球形等壳体密闭结构遭受内外爆炸作用下的响应等做了大量的试验和数值分析。申祖武等^[11]利用ALE算法和炸药爆轰产物JWL状态方程，采用动力分析有限元程序LS-DYNA3D，对二层框架结构建筑物在爆炸冲击波作用下的动力特性进行了数值模拟，并通过结构模型的爆炸试验，得出不同位置处质点压力和加速度时程曲线；凌贤长等^[12]以覆盖饱和砂土层的浅埋地下圆拱直墙式防护隧道免遭炸弹触地爆炸触发冲击波破坏的保护效应为目的，基于Bockingham π定理，采用量纲分析方法，并结合考虑土-结构体系非线性爆炸冲击动力响应、土-结构接触面爆炸冲击动力响应以及爆炸冲击波-结构动力相互作用的相似性，求解了土-结构爆炸冲击相互作用模爆试验的模型设计相似关系。

笔者在现有文献的基础上，综合考虑非线性动力方程的求解方法、材料模型的选取、爆炸冲击波的输入方法、收敛性及流-固耦合效应的实现因素，利用显式动力有限元程序ANSYS/LS-DYNA探讨土体隧道围岩结构在爆炸作用下不同单元的时间历程曲线，分析爆炸作用下土体隧道围岩结构的动力响应。

1 基本理论

在动载作用下，设单元结点在任一时刻发生虚位移δq^e，单元也产生相应的虚位移δd和虚应变δε，则单元内产生的虚应变能为

$ \delta U{\rm{ = }}\int {\int\limits_V {\int {\delta {\mathit{\boldsymbol{\varepsilon }}^{\rm{T}}}} } } \mathit{\boldsymbol{\sigma }}{\rm{d}}V, $

(1)

式中：ρ为材料密度；ν为线性阻尼系数；V为单元体积，加速度引起的惯性力为$ - \rho \mathit{\boldsymbol{\dot d}}{\rm{d}}V $，速度引起的阻尼力为$ - \nu \mathit{\boldsymbol{\dot d}}{\rm{d}}V $，则外力所做的虚功为

$ \begin{array}{l} \delta W = \int {\int\limits_V {\int {\delta {\mathit{\boldsymbol{d}}^{\rm{T}}}} } } {\mathit{\boldsymbol{P}}_{\rm{V}}}{\rm{d}}V + \int {\int\limits_A {\delta {\mathit{\boldsymbol{d}}^{\rm{T}}}} } {\mathit{\boldsymbol{P}}_{\rm{S}}}{\rm{d}}A + \delta {\mathit{\boldsymbol{d}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_{\rm{C}}} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\int {\int\limits_V {\int {\rho \delta {\mathit{\boldsymbol{d}}^{\rm{T}}}} } } \mathit{\boldsymbol{\dot d}}{\rm{d}}V - \int {\int\limits_V {\int {\nu {\mathit{\boldsymbol{d}}^{\rm{T}}}} } } \mathit{\boldsymbol{\dot d}}{\rm{d}}V, \end{array} $

(2)

式中：P_V、P_S和P_C分别为作用于单元上动态体力、动态面力和动态集中力；A为单元面积。

由于

$ \mathit{\boldsymbol{d}} = \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{q}}^e}, \mathit{\boldsymbol{\varepsilon }} = \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{q}}^{\rm{e}}}, \delta U = \delta W, $

(3)

故单元的运动方程为

$ {\mathit{\boldsymbol{m}}^e}{\mathit{\boldsymbol{\dot q}}^e} + {\mathit{\boldsymbol{c}}^e}{\mathit{\boldsymbol{\dot q}}^e} + {\mathit{\boldsymbol{k}}^e}{\mathit{\boldsymbol{q}}^e} = {\mathit{\boldsymbol{R}}^e}\left( t \right), $

(4)

式中：$ \begin{array}{l} {\mathit{\boldsymbol{k}}^e} = \int {\int\limits_V {\int {{\mathit{\boldsymbol{B}}^{\rm{T}}}} } } \mathit{\boldsymbol{DB}}{\rm{d}}\;V, {\mathit{\boldsymbol{m}}^e} = \int {\int\limits_V {\int {{\mathit{\boldsymbol{N}}^T}} } } \rho \mathit{\boldsymbol{N}}{\rm{d}}V, {\mathit{\boldsymbol{c}}^e} = \int {\int\limits_V {\int {{\mathit{\boldsymbol{N}}^{\rm{T}}}} } } \mathit{\boldsymbol{\nu N}}{\rm{d}}\;V, {\mathit{\boldsymbol{R}}^e}\left( t \right) = \int {\int\limits_V {\int {{\mathit{\boldsymbol{N}}^{\rm{T}}}} } } {\mathit{\boldsymbol{P}}_{\rm{V}}}{\rm{d}}\;V + \int {\int\limits_A {\int {{\mathit{\boldsymbol{N}}^{\rm{T}}}} } } {\mathit{\boldsymbol{P}}_{\rm{S}}}{\rm{d}}\;A + {\mathit{\boldsymbol{N}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_{\rm{C}}} \end{array} $。

将各单元特性矩阵组装成整个结构的特性矩阵，即有

$ \mathit{\boldsymbol{M\dot q}} + \mathit{\boldsymbol{C\dot q}} + \mathit{\boldsymbol{K q}} = \mathit{\boldsymbol{R}}\left( t \right), $

(5)

式中：q为所有结点位移分量组成的n节列阵；n为结构总自由度数；$ \mathit{\boldsymbol{R}}\left( t \right) = \sum\limits_{i = 1}^n {{\mathit{\boldsymbol{R}}_i}} \left( t \right) $称为结点载荷列阵；K、M、C分别为结构的刚度矩阵、质量矩阵和阻尼矩阵。

结构的固有特性由结构本身决定，与外部载荷无关，它是由1组模态参数定量描述。固有特性分析就是对模态参数进行计算，一是避免结构出现共振和有害的振型，二是为动力响应分析提供必要的依据。由于固有特性与外载无关，且阻尼对固有频率和振型影响不大，所以可以通过无阻尼自由振动方程计算固有特性。无阻尼自由振动方程为

$ \mathit{\boldsymbol{M\dot q}} + \mathit{\boldsymbol{Kq}} = 0, $

(6)

通过求解可以得到广义特征值方程

$ \left( {\mathit{\boldsymbol{K}}- {\omega ^2}\mathit{\boldsymbol{M}}} \right)\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = 0。$

(7)

2 分析模型

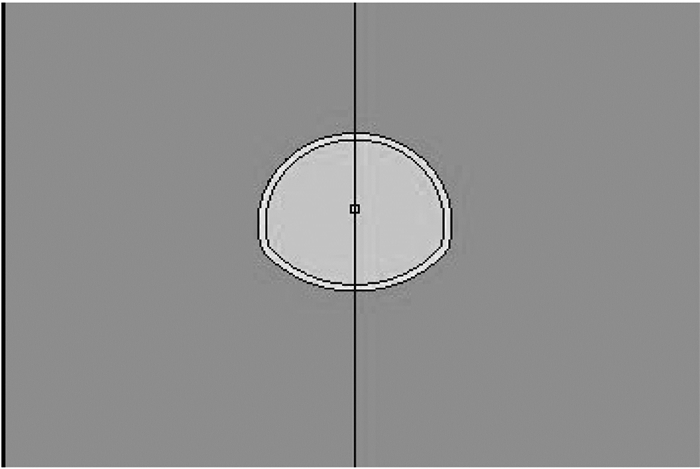
为了模拟高能量的炸药，采用立方体TNT炸药包进行模拟计算，其尺寸为0.4 m×0.4 m×0.4 m，炸药底部边界距底部为15.6 m，隧道净高度为8.8 m，净宽度为9.8 m，隧道衬砌厚度为0.4 m。根据圣维南原理，取周围土体尺寸为隧道宽度的4倍左右，即取模型总高度为40 m，宽度40 m，厚度取8 m，其中土体部分高度为20 m，分析模型如图 1所示。

在ANSYS/LS-DYNA有限元软件中建模，模型主要由土体围岩结构、衬砌结构、空气和TNT炸药4种材料组成。为了准确地模拟隧道中爆炸冲击波的传播过程以及爆炸波对围岩结构的破坏作用过程，避免Lagrange单元网格的形状畸变有可能导致计算的中断，在模拟时将土体、隧道混凝土、空气和炸药4种材料均划分为Euler网格，采用多物质ALE算法，允许同一个网格中包含多种物质，在分析过程中不考虑所有材料的重力作用。数值模拟中由于钢筋混凝土建模的复杂性，采用了整体式对隧道衬砌结构进行建模。有限元分析单元采用三维实体Soild164八节点六面体单元。为了节省计算时间，根据模型的对称性，取其1/4模型进行模拟分析。材料模型共有4种物质：土体；隧道混凝土；空气；炸药。

因为土体本身就具有非线性，土体材料使用了LS-DYNA中的D-P模型，具体参数如表 1所示。

隧道衬砌为0.4 m厚的C25混凝土，采用了Johnson-Holmquist-Concrete模型来模拟具有大应变、大应变率以及较高压力的衬砌结构混凝土材料，其参数见表 2。

采用MAT_NULL材料模型来模拟空气、水等流体材料，该材料模型通常需要与状态方程联用。空气材料参数见表 3。

LS-DYNA有限元程序提供了用于模拟炸药爆炸作用的数值模型，即高能炸药材料模型，并结合1个描述爆炸生成气体压力-体积关系的状态方程。TNT炸药材料参数见表 4。

3 动力有限元分析 3.1 位移时程分析

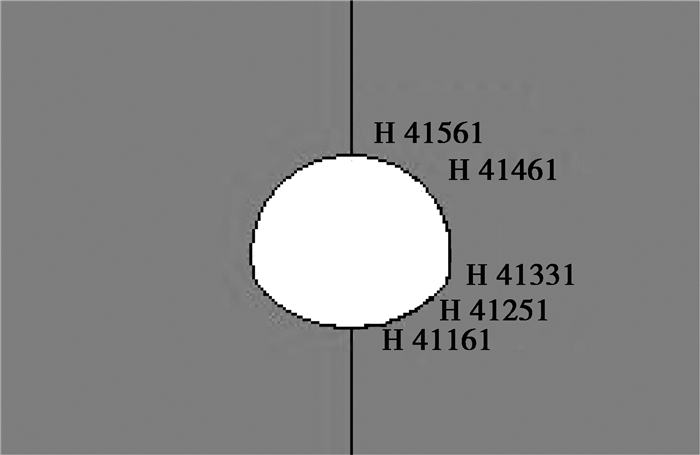
为了便于分析土体隧道围岩结构的动力响应，考虑围岩结构上不同位置处单元的位移情况和隧道结构的对称性，取围岩结构上对应于衬砌结构上的单元，一次取单元41561、41461、41331、41251、41181。参考单元如图 2所示。

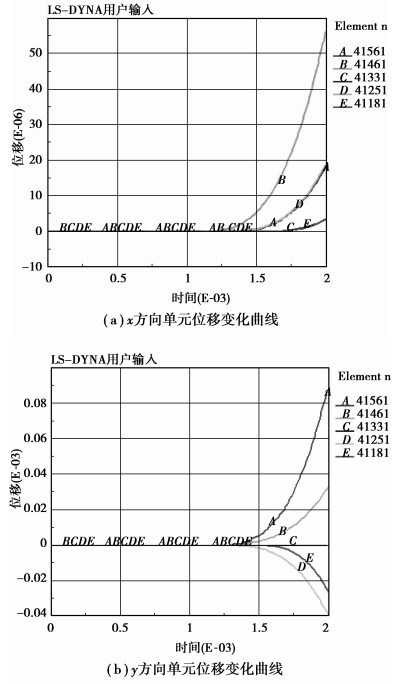
根据LS-DYNA分析，单元41561、41461、41331、41251、41181在x方向和y方向的位移变化曲线如图 3所示。

由图 3可知，不同单元的位移变化不是很大，但对应于衬砌结构顶部和肩部的单元位移较大，如曲线A和曲线B，最大位移0.2 mm左右；其他部位的位移变化不大，这是因为爆炸作用时衬砌结构顶部及肩部的变形过大，就会引起相对应部位围岩结构的位移增大，而位移量较小主要是因为爆炸的大部分能量被隧道衬砌吸收。

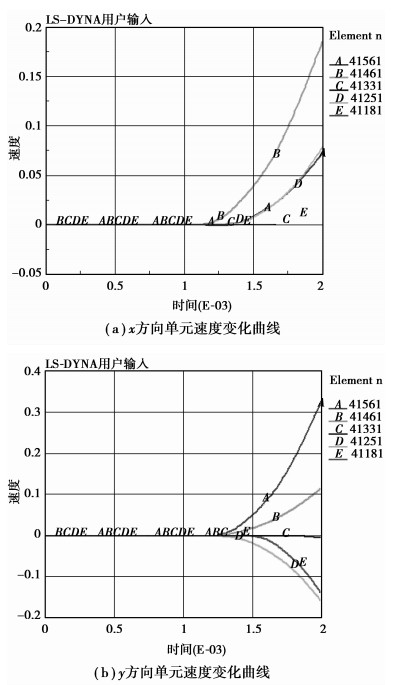
3.2 速度时程分析

在分析隧道围岩结构单元速度时程时，参考单元同上，其速度变化曲线如图 4所示。

对于隧道围岩结构的单元在不同时刻的速度而言，定义竖向速度向上取正值，向下取负值，水平速度向右取正值，向左取负值。由图 4可以看出，在炸药爆炸前期即t＜1.2 ms时，各单元的振动速度均为零，随着时间的增加，围岩结构部分单元的速度开始增加，其中在x方向对应于隧道衬砌结构肩部单元(B曲线)的速度急剧增加，一直呈增加趋势，在y方向，对应于隧道衬砌结构顶部单元(A曲线)的速度随着时间的增加而增大。

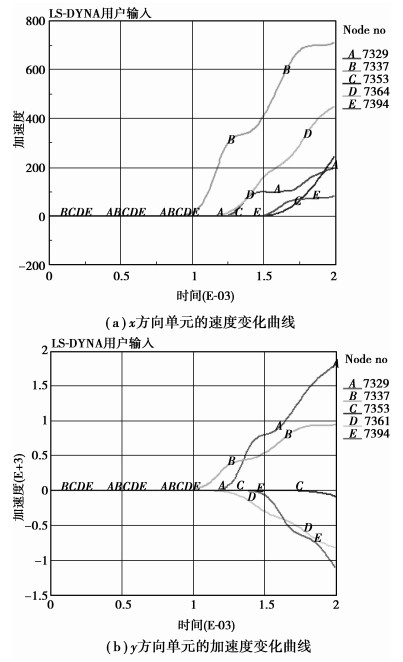
3.3 加速度时程分析

在分析隧道围岩结构单元加速度时程时，参考单元同上，其加速度变化曲线如图 5所示。

爆炸时隧道围岩结构结点在t＜1.0 ms时加速度均为零，随后隧道围岩结构对应于衬砌结构肩部、顶部单元(B曲线和A曲线)的振动加速度峰值最大，各单元的5条加速度变化曲线基本呈增长趋势；加速度峰值波动较大且一次比一次大，由此可见，炸药爆炸冲击波作用时反射和多次反射到对应的围岩结构部位也是比较强烈的。

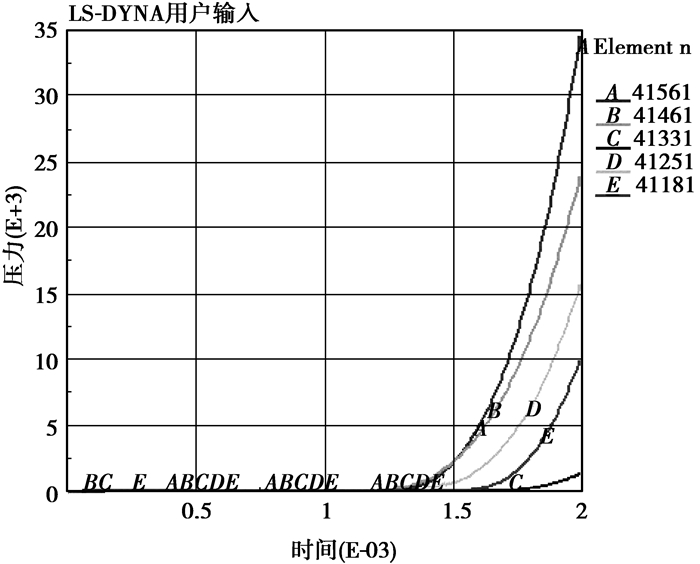
3.4 压力时程分析

在分析隧道围岩结构单元及结点压力时程时，依然取相同的参考单元，其压力变化曲线如图 6所示。

当爆炸冲击波到达隧道围岩结构前，即t＜1.2 ms时隧道围岩结构各部位所受压力均为0；在爆炸冲击波到达隧道围岩结构后，对应于衬砌结构顶部和肩部(即A、B曲线)压力时程曲线波动较大；也就是说对应与衬砌结构的顶部和肩部围岩结构单元损伤威胁较大，最易达到破坏。这是因为当炸药用量较大时，对应于衬砌结构顶部和肩部所吸收的爆炸能和所承受的爆炸冲击波更多的缘故。

3.5 应力时程分析

在分析隧道围岩结构单元及结点应力时程时，依然取相同的参考单元，其应力变化曲线如图 7所示。

隧道围岩结构的最大应力出现在对应于衬砌结构肩部和顶部位置单元和结点，最大有效应力值σ_xmax=-38 kPa，σ_ymax=-64 kPa，τ_max=22.5 kPa。与衬砌结构相比，其值降低幅度较大，超过了土体的容许应力值([σ_u]=56 kPa，[σ_t]=7.3 kPa)；从围岩结构有效应力曲线图可以看出，当爆炸作用对应于衬砌结构顶部和肩部位置最先达到峰值，且有效应力峰值较大，这说明爆炸冲击波作用下此处的土体也最易受损或破坏。

3.6 应变时程分析

采取以上相同的参考单元，其应变变化曲线如图 8所示。

从图 8可知，隧道围岩结构在x向和y向应变最大值分别出现在对应于衬砌结构肩部和顶部的位置，且随着时间的增加呈增长的趋势。从隧道围岩结构的有效塑性应变图可以看出，最大值集中在对应于衬砌结构顶部和肩部位置，这和应力分析的结果很吻合。但围岩结构的单元应变值较小，这说明爆炸时大部分能量被衬砌吸收了的缘故，所以围岩结构受创就较小。

4 结论

通过建立土体隧道动力分析有限元整体模型，综合考虑非线性动力方程的求解方法、材料模型的选取、爆炸冲击波的输入方法、收敛性及流——固耦合效应的实现因素，利用显式动力有限元程序ANSYS/LS-DYNA进行数值模拟，探讨了土体隧道围岩结构在爆炸作用下不同单元的时间历程曲线，分析了爆炸作用下土体隧道围岩结构的动力响应问题，并得到如下结论。

1) 对应于衬砌结构肩部和顶部的围岩结构的单元位移都较大，爆炸作用对这2处的损伤较大，如果炸药能量继续增强将会使其首先在这2处发生破坏。

2) 在爆炸前期，各单元的振动速度均为零，随着时间的增加，对应于衬砌结构肩部的单元的速度急剧增加，而后开始衰减，并会出现最大的负速度，呈周期变化趋势，在整个爆炸过程，其速度始终是增加的。

3) 对应于隧道衬砌结构顶部、肩部的单元的振动加速度峰值最大，但最终加速度基本趋近于零，加速度曲线均出现了2次峰值或多次峰值，由此可见，爆炸冲击波的反射和多次反射现象是比较强烈的。

4) 当爆炸作用到达隧道围岩结构迎爆面时，隧道围岩结构各部位所受应力均为零，随后其结点的压力时程曲线明显不同，对应于顶部、肩部及底部的单元压力时程曲线波动较大，是最易发生损伤或破坏的部位。