2. 中国科学院 寒区旱区环境与工程研究所冻土工程国家重点实验室, 兰州 730000;
3. 长安大学 特殊地区公路工程教育部重点实验室, 西安 710064
2. State Key Laboratory of Frozen Soil Engineering, Cold and Arid Regions Environmental and Engineering Research Institute, Chinese Academy of Sciences, Lanzhou 730000, China;
3. Key Laboratory for Special Area Highway Engineering of Ministry of Education, Chang'an University, Xi'an 710064, China
常温下土体中水分的迁移主要是由基质势和重力势引起的,对于季节性冰冻土体和多年冻土而言,地下水不仅在基质吸力和重力作用下会上升,同时在温度梯度影响下也向上迁移。温度梯度对土体介质中水分迁移产生的直接影响很小,但间接作用很大。比如相变、冻结和融化过程,由于温度分布不均匀会导致未冻水含量的分布不均匀,从而引起介质基质势的变化,引起水分迁移。同时水分的迁移变化又会影响土体的热特性参数,从而影响土体温度场的分布。因此,土体内部水分运动及含水量分布是与其热流及温度分布相互联系,相互作用的[1-6]。
通过对土的冻胀机理及冻土地区路基病害的进一步研究,人们已经认识到冻结过程中的水分迁移是引起路基病害的首要原因[7-11]。图 1显示了冻结过程水分迁移试验结束时土样照片。可以看到,冻结过程水分迁移所引起的分凝聚冰现象是非常显著的,由此所诱发的路基土体的分凝冻胀是非常严重的。因此,有必要进一步加强土体冻结过程水分迁移的试验研究,建立适合分析冻土地区路基冻胀机制的理论模型,从而定量分析由于水分迁移所引起的路基病害,为冻胀防治提供依据。基于此,从封闭系统下土体单向冻结过程水分迁移试验入手,通过对土体内部含水量和温度变化过程的分析,揭示土体冻结过程中水分的迁移变化规律。最后,基于冻结过程水热耦合的基本方程和有限元数值模拟方法模拟计算土体内部温度场和水分场的变化过程。

|
图 1 冻结过程土体分凝聚冰图片 |
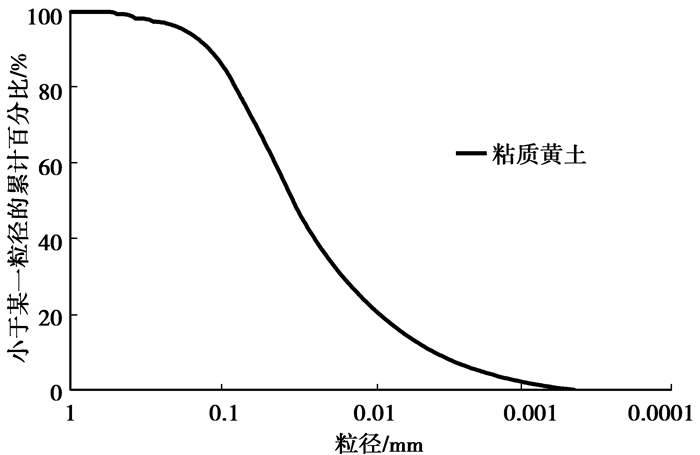
试验所用土体为东北粘质黄土,取自在建沈哈线路堑挖方试验段DK691+820处,取样深度为天然地表下8 m,土样具有一定的代表性。其颗粒级配曲线如图 2所示,土性参数列于表 1。
|
图 2 粘质黄土颗粒级配曲线 |
| 表 1 试验土样的物性参数 |
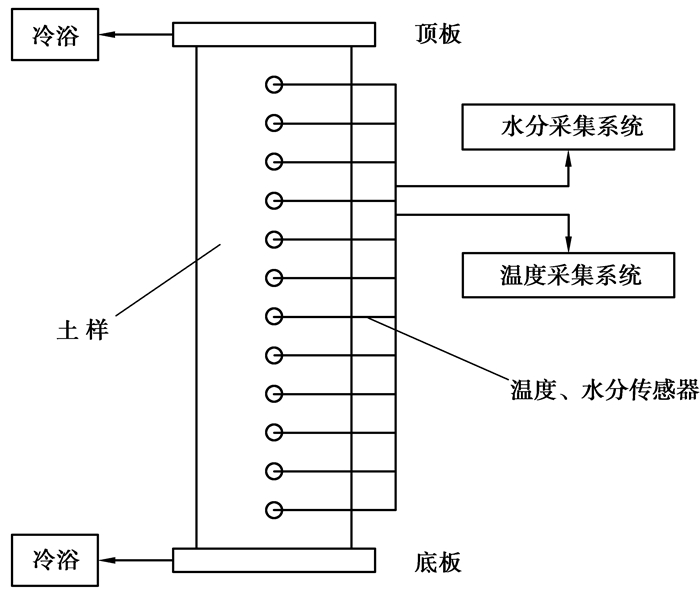
试验装置为长安大学特殊地区公路工程教育部重点实验室自行研究开发的水分迁移测试系统,此系统由试模、水分传感器、温度传感器、水分采集设备、温度采集设备、冷浴装置等部件构成,如图 3和图 4所示。试模采用有机玻璃筒,其高为60 cm,直径为20 cm;水分传感器采用美国SEC水分传感器,精度为0.1;温度传感器的精度为0.1 ℃;水分采集设备为时域反射仪(6050X1 Trase System);控温冷浴循环器的型号为NESLAB LT-50DD,控温范围为-50~+40 ℃,控温误差为±0.03 ℃。

|
图 3 冻结过程土体水分迁移测试系统实体图 |
|
图 4 冻结过程土体水分迁移测试系统示意图 |
试验采用东北粘质黄土,将烘干的土样粉碎后过2 mm筛,配制成质量含水量为29.47%的土样;再经过24 h以上的闷料;然后采用人工击实的方法将土分层装入试件模中,经击实使其达到要求的密实状态;同时每5 cm埋设1支水分传感器和温度传感器,而且水分传感器和温度传感器埋设在同一层,但两者要在水平方向隔开一定距离。
将装好的试件放置24 h,然后将土体侧面及顶部用保温材料包裹好,防止外界温度对土体的干扰。然后开启冷浴装置,使顶板温度控制在-10 ℃,底板温度控制在+2 ℃。应用水分和温度采集设备定时记录土体内部含水量的迁移变化和温度的变化值。
当冻结土体长度在较长时间内不再发生变化时(即通过温度采集设备观察到土体0 ℃位置不再向下移动时),关闭冷浴装置,撤掉外层的保温装置,并在试件顶端施加20 ℃左右的温度,使土体融化,定时记录土体内部的含水量和温度。土体全部融化后,停止试验,进行数据的整理和分析。
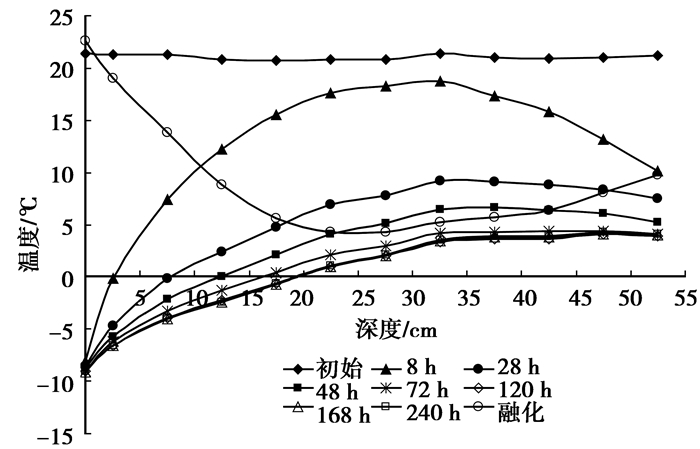
1.4 试验结果分析 1.4.1 温度场的分布及其分析图 5所示为不同时刻温度随试样深度的变化曲线。可以看出,试件在降温初期温度变化比较大,土样在降温8 h时顶部土体已发生冻结(文中以0 ℃作为冻土段和未冻土段的分界点,即以0 ℃作为土体的冻结温度)。此外,在试验过程中试样是从两端开始降温(顶端温度控制为-10 ℃,底端温度控制为+2 ℃), 因而在降温初期土体温度是由中部到两端逐渐降低,温度曲线呈现出开口向下的抛物线变化。随着冻结时间的推移,土体温度场的变化逐渐减小,最终趋向于稳定。此时,土体内部温度大致分成2段:已冻土段和未冻土段,并且已冻土段的温度梯度大于未冻土段,其拐点大约在0 ℃附近。融化阶段,试样温度是从两端开始升温,因此土体温度是由中部到两端逐渐升高,温度曲线呈现出开口向上的抛物线变化。
|
图 5 不同时刻温度随试样深度的变化曲线 |
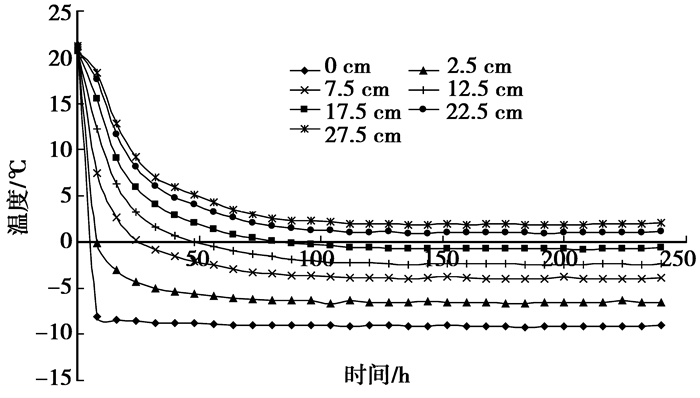
试样不同深度处温度传感器随时间的变化趋势见图 6。为方便做图,这里只给出试件上部7个温度传感器测试数据的变化规律。图中表明,在降温初期,土样冷端处的温度急剧降低,随着冻结时间的增长,降温的速率逐渐减小,最终维持在一个稳定的温度数值。随试样深度的增大,温度变化表现出相似的变化规律,但降温速率和温度降低的幅度逐渐减小,最终土体内部温度随深度的变化呈现出一个稳定的温度梯度分布。此外,从图中可以看出,在距冷端约17.5 cm的范围之内,试样出现冻结,为试样的冻结区;其下土体在试验过程中一直未发生冻结,为试样的未冻区。
|
图 6 试样不同深度温度随时间的变化曲线 |
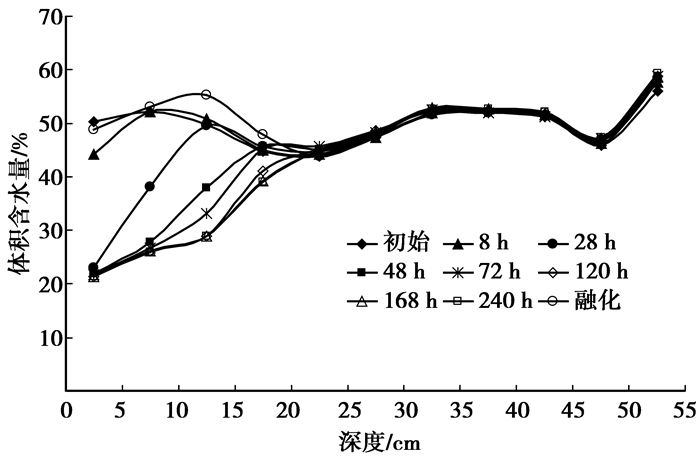
图 7为试样经历不同时间后的含水量分布。可以看出,冻结前试样中初始含水量测试结果并非全部均匀一致,这是由于土样拌和、装样及水分传感器测试误差所致。结合图 5,在试验开始阶段(顶部土体温度到达0 ℃之前)试件降温幅度比较大,尽管土体内部已出现较大的温差,但整个土体温度在正温范围内,此时对应的土体内部的含水量无明显变化,这表明在正温范围内温度梯度对水分迁移的影响很小,亦即由于温差存在所引起的温度势对水分迁移的影响甚微。随着冻结时间的推移,试样在8 h时顶部土体含水量已经开始减小。此时顶部已处于冻结状态,顶部含水量减小是因为土体内部水分发生冻结的缘故(此时所测水分为冻土中的未冻水含量)。随着冻结深度的前移,试样上部冻结区含水量随时间的变化逐渐减小,当土体内部温度场达到稳定时,上部冻结区含水量不再减小,达到某一负温下的相对稳定值。值得注意的是,冻结稳定时在与冻结锋面(深度约为17.5 cm处)邻近的未冻区含水量减小,其下水分传感器的测试数据基本无变化。分析其原因,冻结锋面邻近未冻区含水量减小是因为水分在温度梯度的作用下迁移到冻结区的缘故,这证明了水分有向冻结区迁移的倾向。前面的分析已经表明温度势对水分迁移的影响甚微,水分在温度梯度作用下之所以向冻结区迁移是因为当温度的变化致使土体发生冻结时,冻结区的液态水含量急剧减小,从而引起其基质势能的急剧降低,促使土中未冻水沿着温度降低的方向迁移。此外,由于试验采用的土样为高液限粘质黄土,其渗透系数的数量级相对比较小,导致其水分迁移的速率是比较小的,加上试验时间的限制,冻结过程中下部未冻区水分来不及向上迁移,因而下部未冻区水分传感器的测试数据基本无变化。由土样融化后的含水量曲线也可以看出,与初始含水量相比,顶部含水量略有增加,这进一步说明冻结邻近未冻区含水量在温度梯度作用下向顶部发生了迁移。另外,靠近冷板处的含水量在冻结前后基本无变化,主要原因在于该范围(约2.5 cm)的土体快速冻结,水分迁移不充分,该现象称之为人工冻结试验的“顶端效应”。
|
图 7 不同时刻体积含水量随试样深度的变化曲线 |
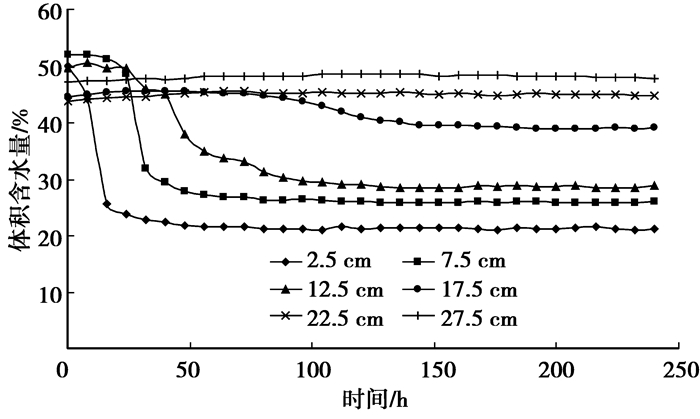
图 8所示为不同深度处水分传感器测试数据随时间的变化趋势。为方便作图,这里只给出试件上部6个水分传感器测试数据的变化规律。从图中可以看出,土样上部2.5、7.5、12.5、17.5 cm处水分传感器测出的含水量变化较大,说明在此处必然出现冻结现象,产生冰晶体。前面温度场分析时已经知道,上述水分传感器相应深度处的温度传感器测试数据出现负温,因而温度场测试数据与水分场测试数据是相吻合的。此外,图中揭示出冻结过程中下部未冻区水分传感器测试数据无明显变化,原因在前面分析时已经指出,主要与土质及试验的时间有关。
|
图 8 试样不同深度体积含水量随时间的变化曲线 |
根据能量守恒定律,若不考虑对流传热和蒸发潜热,仅考虑介质的热传导和冰水相变问题,则二维形式的热流输运方程可表示如下
| $ \rho C\frac{{\partial T}}{{\partial t}} = \frac{\partial }{{\partial x}}\left( {\lambda \frac{{\partial T}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {\lambda \frac{{\partial T}}{{\partial y}}} \right) + L{\rho _{\rm{i}}}\frac{{\partial {\theta _{\rm{i}}}}}{{\partial t}}, $ | (1) |
式中:C为路基土的比热;λ为路基土的导热系数;θi为体积含冰量;ρi为冰的密度;ρ为路基土的密度;T为路基土的温度;L为冰的融化潜热。
应用显热容法[12],假设相变是发生在Tm附近的一个温度范围(Tm±ΔT)内,导热系数λ和比热C在固相和液相区分别取为λf、λu、Cf、Cu,构造的热容表达式和导热系数的表达式为
| $ C = \left\{ \begin{array}{l} {C_{\rm{f}}},T < {T_{\rm{m}}} - \Delta T,\\ \left( {{C_{\rm{f}}} + {C_{\rm{u}}}} \right)/2,{T_{\rm{m}}} - \Delta T \le T \le {T_{\rm{m}}} + \Delta T,\\ {C_{\rm{u}}},T > {T_{\rm{m}}} + \Delta T。\end{array} \right. $ | (2) |
| $ \begin{array}{l} \lambda = \\ \left\{ \begin{array}{l} {\lambda _{\rm{f}}},T < {T_{\rm{m}}} - \Delta T,\\ {\lambda _{\rm{f}}} + \frac{{{\lambda _{\rm{u}}} - {\lambda _{\rm{f}}}}}{{2\Delta T}}\left[ {T - \left( {{T_{\rm{m}}} - \Delta T} \right)} \right],{T_{\rm{m}}} - \Delta T \le T \le {T_{\rm{m}}} + \Delta T\\ {\lambda _{\rm{u}}},T > {T_{\rm{m}}} + \Delta T。\end{array} \right. \end{array} $ | (3) |
根据修正的达西定律亦即白金汉-达西定律,非饱和土体中水分流动所应满足的运动方程可以表示如下
| $ \begin{array}{*{20}{c}} {V = - K\left( {{\theta _{\rm{u}}}} \right)\nabla \psi = - K\left( {{\theta _{\rm{u}}}} \right)\nabla \left( {{\psi _{\rm{m}}} + z} \right) = }\\ { - K\left( {{\theta _{\rm{u}}}} \right)\nabla \left( {\frac{p}{{{r_{\rm{w}}}}} + z} \right),} \end{array} $ | (4) |
式中:V为渗流速度;θu为土体体积液态水含量(在冻土内就是未冻水含量);K(θu)为非饱和渗透系数,为液态体积含水量或饱和度的函数;ψ为土水总势能;ψm为基质势;z为重力势;p为孔隙负压;rw为水的容重。
根据质量守恒定律,假定空气和水蒸气迁移对于纯水迁移的影响可以忽略,则非饱和冻土二维形式的连续性方程可以表示如下
| $ \frac{{\partial {\theta _{\rm{u}}}}}{{\partial t}} + \frac{{{\rho _{\rm{i}}}}}{{{\rho _{\rm{w}}}}}\frac{{\partial {\theta _{\rm{i}}}}}{{\partial t}} = - \left[ {\frac{{\partial {V_x}}}{{\partial x}} + \frac{{\partial {V_y}}}{{\partial y}}} \right], $ | (5) |
式中:Vx,Vy为x,y 2个方向上的渗流速度;ρw为水的密度;t为时间。
将运动方程式(4)代入连续性方程式(5)中,非饱和土冻结和融化过程二维形式的水分运动偏微分方程可以表示如下
| $ \frac{{\partial {\theta _{\rm{u}}}}}{{\partial t}} + \frac{{{\rho _{\rm{i}}}}}{{{\rho _{\rm{w}}}}}\frac{{\partial {\theta _{\rm{i}}}}}{{\partial t}} = \frac{1}{{{r_{\rm{w}}}}}\frac{\partial }{{\partial x}}\left[ {K\frac{{\partial p}}{{\partial x}}} \right] + \frac{1}{{{r_{\rm{w}}}}}\frac{\partial }{{\partial y}}\left[ {K\frac{{\partial p}}{{\partial y}}} \right] + \frac{{\partial K}}{{\partial y}}, $ | (6) |
式中的K为综合导水系数,它可以表示为
| $ K = \left\{ \begin{array}{l} {K_{\rm{f}}},T < {T_{\rm{m}}} - \Delta T,\\ \left( {{K_{\rm{f}}} + {K_{\rm{u}}}} \right)/2,{T_{\rm{m}}} - \Delta T \le T \le {T_{\rm{m}}} + \Delta T,\\ {K_{\rm{u}}},T > {T_{\rm{m}}} + \Delta T。\end{array} \right. $ | (7) |
引入总体积含水量θ
| $ \theta = {\theta _{\rm{u}}} + {\theta _{\rm{i}}}。$ | (8) |
这样,热量传递方程(1)、水分迁移方程(6)及方程(8)组成了描述非饱和渗流场与温度场耦合问题的控制微分方程组。此方程组中包括5个未知函数θ、θu、T、θi、p,所以必须另外引入2个补充方程才能求解,在这里首先根据室内试验引入未冻水含量与温度的关系函数
| $ {\theta _{\rm{u}}} = f\left( T \right),T < {T_{\rm{f}}}, $ | (9) |
式中Tf为土中孔隙水的起始冻结温度。
其次,根据室内试验引入非饱和土体孔隙水压力与体积液态水含量之间的定量关系函数(土水特征曲线)
| $ p = p\left( {{\theta _{\rm{u}}}} \right)。$ | (10) |
热量传递方程(1),水分迁移方程(6)、方程(8)~(10)及一定的初始条件和边界条件组成了描述非饱和正冻土水热耦合过程完整的偏微分方程组,由于属于拟线性偏微分方程组,目前无法用解析法或半解析法求解,需要利用有限元方法进行数值求解。
2.2 数值计算模型与参数 2.2.1 数值模型基于封闭系统下土体单向冻结过程水分迁移试验的试样尺寸,计算过程中土体高度取为57.5 cm,直径为20 cm。另外,考虑到模型的轴对称特性,计算中为了减少单元和节点数目,可取其中一个轴对称平面进行计算,其网格划分的剖面图如图 9所示,模型中共有92个单元和331个节点。

|
图 9 数值计算网格模型 |
模型两端温度属于第一类边界条件,通过对实测温度数据进行回归分析,得出试样两端温度随时间的变化规律。
| $ \begin{array}{l} 顶板处\left( {y = 57.5} \right):\\ \left. \begin{array}{l} T = 2.4095{t^2} - 17.357t + 23.733,\;\;\;0 \le t \le 3.5h\\ T = 0.0394{t^2} - 0.7245t - 4.7576,3.5h < t \le 8h\\ T = - 0.0143t - 8.177,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;8h < t \le 58h\\ T = - 9.1,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;58h < t \le 244h \end{array} \right\}, \end{array} $ | (11) |
| $ \begin{array}{l} 底板处\left( {y = 0} \right):\\ \left. \begin{array}{l} T = 0.8913{t^2} - 6.9354t + 20.998,\;\;\;\;0 \le t \le 4h\\ T = 0.0545{t^2} - 1.2545t + 11.539,\;\;\;\;\;4h < t \le 8h\\ T = - 0.2133t + 6.7222,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;8h < t \le 12h\\ T = 4,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;12h < t \le 244h \end{array} \right\}。\end{array} $ | (12) |
土体侧面已用保温材料包裹好,因而模型两侧温度属于绝热边界条件,即
| $ \frac{{\partial T}}{{\partial n}} = 0。$ | (13) |
由于试验是在封闭系统下(无补水条件)进行,因而模型四周均为不透水边界,用公式可以表示为
| $ - \frac{k}{{{r_{\rm{w}}}}}\left( {l\frac{{\partial p}}{{\partial x}} + m\frac{{\partial p}}{{\partial y}}} \right) - km = \overline {{v_n}} = 0, $ | (14) |
式中:l,m分别为边界外法线方向余弦;
根据现场实测及有关参考资料[13],将计算中所需的热物理参数归纳为表 2。
| 表 2 试验土样热物理参数 |
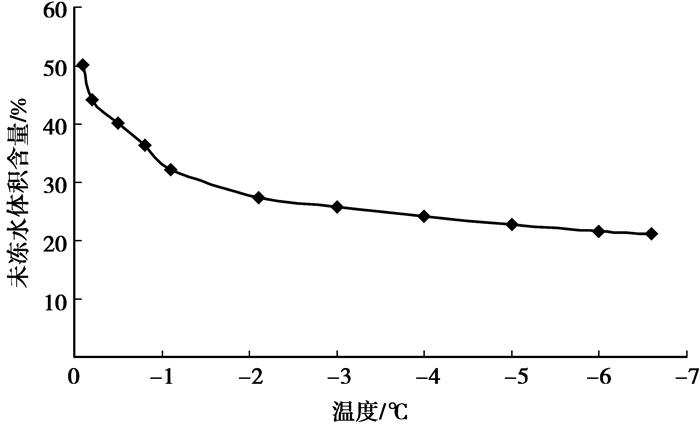
不同温度下土样未冻水体积含量的测试结果如图 10所示。
|
图 10 粘质黄土未冻水体积含量随温度的变化 |
由图可见,未冻水含量始终和负温保持动态平衡关系,可表示为
| $ {\theta _u} = f\left( T \right) = a{T^b}, $ | (15) |
式中:θu为未冻水含量,%;T为负温绝对值,℃;a和b为与土质因素有关的经验常数。
| 表 3 未冻水含量与温度的关系 |
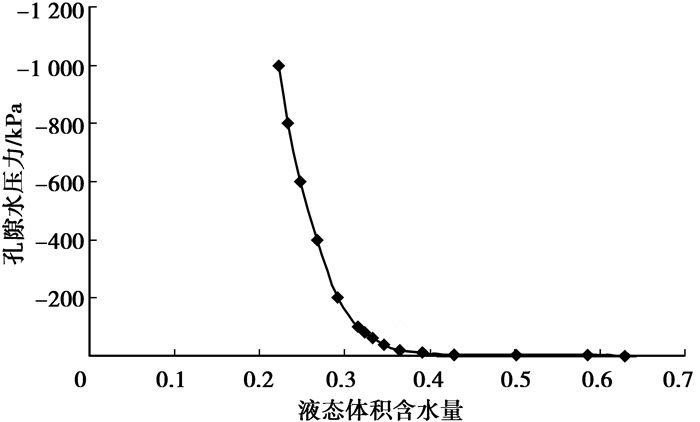
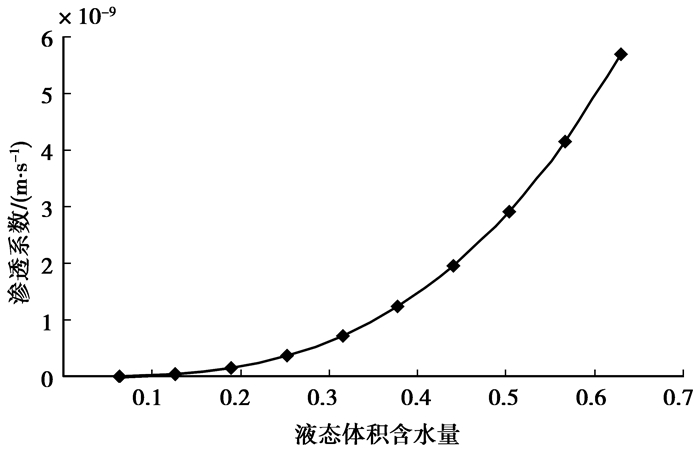
计算模型采用的土水特征曲线由日立高速冰冻离心机法测得的土水特征曲线经过拟合分析得到[14],见图 11。计算过程中所采用的非饱和渗透系数如图 12所示,进行曲线拟合,可以得到非冻结区土体导水系数的表达式为
| $ {K_{\rm{u}}} = 2.28 \times {10^{ - 8}}\theta _{\rm{u}}^3。$ | (16) |
|
图 11 土-水特征曲线 |
|
图 12 渗透系数随液态体积含水量的变化 |
冻土中冰的存在阻断了部分水流通道,使得冻土的导水能力有所下降,故在研究冻土水热迁移问题中引入阻抗系数I的概念[15],认为冻土的导水率降低到相同未冻水含量融土的1/I。阻抗系数的大小取决于土体中体积含冰量θi的多少,可用下式表示
| $ I = {10^{10{\theta _{\rm{i}}}}}。$ | (17) |
由此,冻结区土体导水率的值可以表示为
| $ {K_{\rm{f}}} = {K_{\rm{u}}}/I。$ | (18) |
利用大型有限元分析软件abaqus 6.8建立了温度场和水分场的耦合计算平台,通过二次开发编写了计算程序,对前面所建立的非饱和正冻土水热耦合数学模型进行有限元计算,并与试验结果进行对比。
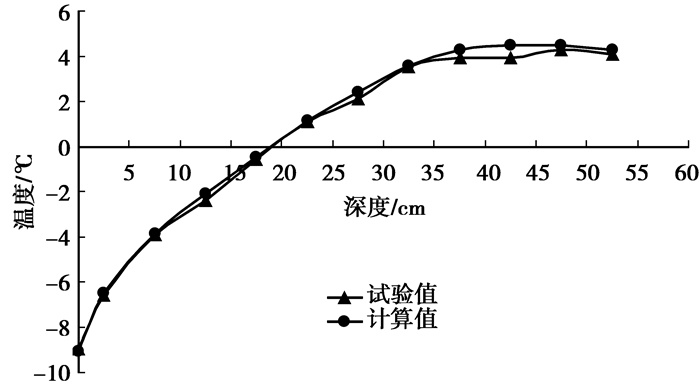
2.3.1 温度场分析在实际情况中,往往关心的是最终结果,所以选取t=240 h冻结稳定时土体温度场的计算值和试验值进行对比分析。图 13为试验温度和计算温度的对比。可以看出:模型计算温度较为平顺,试验温度变化相对较多,但土体计算的温度曲线符合试验的规律,与试验值吻合较好(最大误差0.6 ℃左右),即试样冻结段温度梯度较大,到试样未冻结段较小。因此用温度场与水分场耦合模型计算封闭系统土体内部温度场的变化是可行的。分析误差产生的原因,一是由于试验过程中人为因素比较大,并且测量仪器的精确度不高,造成试验值本身存在一定误差;第二,冻土是复杂的多相体,涉及到相的转变,热交换参数和水力参数对最终的计算结果影响很大,但参数的测定始终是个难点,特别是导水系数和土水势并无成熟的测定方法,会带来较大的误差。
|
图 13 试样在第240 h不同深度温度的计算值和试验值比较图 |
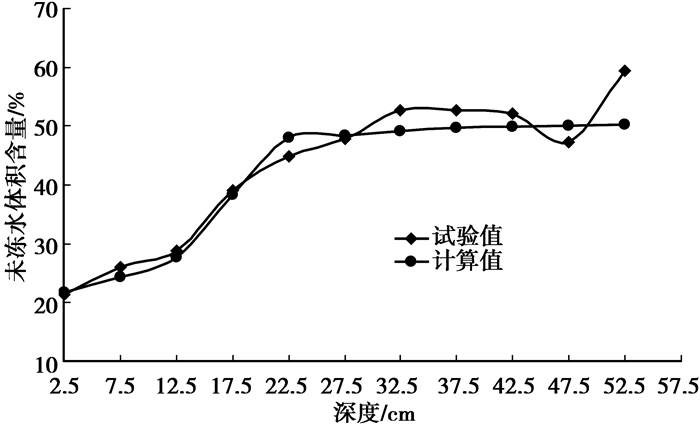
与温度场的分析相对应,选取t=240 h冻结稳定时土体未冻水体积含量的计算值和试验值进行对比分析。图 14为未冻水含量试验测试值和计算值的对比。可以看出,未冻水含量的计算值和试验值曲线基本吻合,都表现为冻结后未冻水含量在冻土段(试样表面以下约17.5 cm深度内)减小较大,冻结后冻土段的液态孔隙水部分被冻结。由此,该耦合模型计算封闭系统土体内部水分场的变化亦是可行的。值得注意的是,未冻水含量计算值和试验值仍然存在些许差异,尤其是在试件的融土段,最大误差在10%左右,分析其原因主要是在设置初始条件产生误差。
|
图 14 试样在第240 h不同深度未冻水含量的计算值和试验值比较图 |
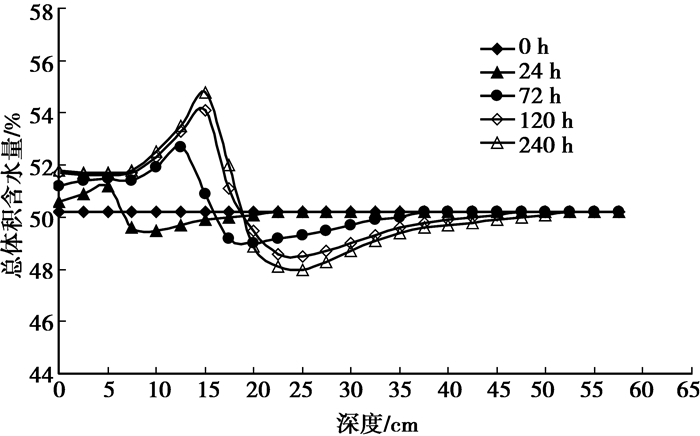
为了进一步揭示土体冻结过程中水分的迁移变化特征,作出不同冻结时间总体积含水量计算值沿试样高度的分布曲线,如图 15所示。可以看到一个总的趋势,即经过一定的冻结时间后,试样上部的总体积含水量增大。经过240 h的冻结后,总体积含水量计算值与前面试样融化后总体积含水量的试验观测值基本吻合(见图 7),即含水量增大的范围主要集中在冻结段(试样表面以下约17.5 cm深度内),而17.5 cm到50 cm的深度内总含水量却产生部分下降,在50 cm以下的总含水量基本保持不变。分析其原因是,随着冻结过程,孔隙水在土水势梯度的作用下源源不断的向冻结锋面迁移,然后被冻结成固体冰,所以在冻土段总含水量(包括未冻水和冰)将大于初始含水量。冻结层下的孔隙水在温度梯度的作用下向上迁移后,又没有毛细水的补给,所以未冻结段的含水量减小。值得注意的是,试样总体积含水量计算值与试验值之间仍然存在一定差异,原因主要是设置含水量的初始条件以及水分运动参数的选取产生误差。此外,冻结稳定后试样含水量产生突增位置在15 cm左右,此处的温度在-2~0 ℃之间(具体数值约为-1.2 ℃),位于冻土的相变温度区间之内,因而此处产生冻结锋面,致使试样下部水分向冻结锋面迁移;在25 cm处含水量最小,分析其原因在于该处的水分向上迁移,而试验采用的土样为高液限粘质黄土,其渗透系数的数量级相对比较小,导致其水分迁移的速率较小,加上试验时间的限制,致使下部的水分不能及时补给土柱的中层。
|
图 15 不同冻结时间试样不同深度总含水量的变化 |
1) 以沈哈高速铁路沿线的粘质黄土为研究对象,对土样冻结过程中封闭系统下的水分迁移过程进行了水分场和温度场的动态试验观测。
2) 试验结果表明,降温初期试样温度变化较快,随着冻结时间的推移,土体温度场的变化逐渐减小,最终试样内部温度随深度的变化呈现出一个稳定的温度梯度分布。温度势对水分迁移的影响甚微;温度梯度是导致含水量梯度产生的一个重要诱导因素,当温度的变化致使土体发生冻结时,冻结区的液态水含量急剧减小,从而引起其基质势能的急剧降低,促使土中未冻水沿着温度降低的方向迁移。
3) 在试验研究的基础上,基于能量平衡原理和质量守恒定律,建立了非饱和正冻土二维温度场和水分场耦合效应模型,并应用有限元数值方法对室内封闭系统下模型试件的温度场、水分场进行了数值模拟。
4) 通过数值模拟结果可以看出,试样温度、未冻水含量以及总体积含水量的试验观测值与计算值基本吻合,其中温度和未冻水含量的最大误差分别在0.6 ℃和10%左右。因此,数值模拟可以较好地反映非饱和正冻土冻结过程中温度场和水分场的发展变化过程。该模型可用于模拟季节性冰冻地区路基土体中水分迁移的变化规律,为冻胀防治提供依据。
| [1] |
汪仁和, 李栋伟.
正冻土中水热耦合数学模型及有限元数值模拟[J]. 煤炭学报, 2006, 31(6): 757–760.
WANG Renhe, LI Dongwei. Moisture-temperature coupling mahematical model in freezing soil and fnite element numerical simulation[J]. Journal of China Coal Society, 2006, 31(6): 757–760. (in Chinese) |
| [2] |
毛雪松, 王秉刚, 胡长顺, 等.
冻土路基水热迁移问题的理论模型及数值模拟[J]. 中外公路, 2006, 26(1): 23–26.
MAO Xuesong, WANG Binggang, HU Changshun, et al. A theoretical model of moisture and heat transfer for frozen soil subgrade and numerical simulation[J]. Journal of China & Foreign Highway, 2006, 26(1): 23–26. (in Chinese) |
| [3] |
马琳, 王清, 原国红.
长春地区季节冻土水热迁移的分析与模拟[J]. 辽宁工程技术大学学报:自然科学版, 2010, 29(1): 52–55.
MA Lin, WANG Qing, YUAN Guohong. Analysis and simulation of moisture and heat translocation in seasonal freezing soil in Changchun[J]. Journal of Lianing Technical University:Natural Science, 2010, 29(1): 52–55. (in Chinese) |
| [4] | Wang T H, Su L J. Experimental study on moisture migration in unsaturated loess under effect of temperature[J]. Journal of Cold Regions Engineering, 2010, 24(3): 77–86. |
| [5] | Heitman J L, Horton R, Ren T, et al. An improved approach for measurement of coupled heat and water transfer in soil cells[J]. Soil Science Society of America Journal, 2007, 71(3): 872–880. |
| [6] | Heitman J L, Horton R, Ren T, et al. A test of coupled soil heat and water transfer prediction under transient boundary temperatures[J]. Soil Science Society of America Journal, 2008, 72(5): 1197–1207. |
| [7] |
张树光, 屈小民.
非等温条件下道路水分迁移的数值模拟[J]. 岩土力学, 2004, 25(Sup2): 231–234.
ZHANG Shuguang, QU Xiaomin. Numerical simulation of moisture migration in roadway under condition of transient temperature[J]. Rock and Soil Mechanics, 2004, 25(Sup2): 231–234. (in Chinese) |
| [8] |
谷宪明, 王海波, 梁士忠, 等.
季冻区路基土水分迁移数值模拟分析[J]. 公路交通科技:应用技术版, 2007, 9: 51–54.
GU Xianming, WANG Haibo, LIANG Shizhong, et al. Numerical simulation of moisture migration in subgrade soil in seasonal froen ground[J]. Journal of Highway and Transportation Research and Development:Applied Technique, 2007, 9: 51–54. (in Chinese) |
| [9] | 王威娜. 季节性冰冻地区路基变形数值模拟[D]. 西安: 长安大学硕士学位论文, 2009. |
| [10] |
宋存牛, 王选仓.
季节冻土区风积沙土路基冻结过程中水热迁移数值分析[J]. 冰川冻土, 2007, 29(6): 997–1003.
SONG Cunniu, WANG Xuancang. Numerical analysis of coupled mosture and heat transfer within a freezing aeolian sandy embankment in seasonally frozen soil regions[J]. Journal of Glaciology and Geocryology, 2007, 29(6): 997–1003. (in Chinese) |
| [11] | Mao X S, Hou Z J, Ma B. Affection of the seeping of accumulative water on the thermal stability of the subgrade along Qinghai-Tibet highway[C]//Proceedings of the Eighth International Symposium on Pemafrost Engineering, October 14-17, 2009, Xi'an, China. Beijing:Chinese Academy of Science, 2009:63-69. |
| [12] | Lai Y M, Wang Q S, Niu F J, et al. Three-dimensional nonlinear analysis for temperature characteristic of ventilated embankment in permafrost regions[J]. Cold Regions Science and Technology, 2004, 38(2/3): 165–184. |
| [13] |
刘为民, 何平, 张钊.
土体导热系数的评价与计算[J]. 冰川冻土, 2002, 24(6): 770–773.
LIU Weimin, HE Ping, ZHANG Zhao. A calculation method of thermal conductivity of soils[J]. Journal of Glaciology and Geocryology, 2002, 24(6): 770–773. (in Chinese) |
| [14] | 许健. 季节冻土区路基土体冻胀机理及防治工程效果研究[D]. 北京: 中国科学院大学博士学位论文, 2010. |
| [15] | Tailor G S, Luthin J N. A model for coupled heat and moisture transfer during soil freezing[J]. Canadian Geotechnical Journal, 1978, 15(4): 548–555. |
 2013, Vol. 36
2013, Vol. 36


