隧道工程在交通建设中的数量越来越多、规模越来越大、地位越来越重要,且大量已建成和拟建的隧道工程都位于中国地震活动频繁的西南地区、西北地区、华北地区、东南沿海的广东、福建地区以及台湾省及其附近海域的23条地震带上,必须对其抗震计算方法予以高度重视[1]。目前,中国交通行业参照的隧道抗震规范主要有《公路工程抗震设计规范JTJ 044-89》、《地铁设计规范》以及《铁路工程抗震设计规范》。根据震害调查和试算,规范[2]规定:在Ⅲ级及以上围岩条件较差的洞口、浅埋、偏压隧道和明洞,以及穿越地质不良地质地带的区域,地震烈度大于7度时,需要进行抗震设计。抗震计算方法规定为地震系数法。在实际工程应用中,对高烈度区深埋隧道采用地震系数法计算所得到的结构地震附加内力与工程实际及震害现象严重不符[3-4]。这是由于地震系数法在隧道埋深增大到一定程度后夸大了地震惯性力的影响,这与地下结构的振动特性不符。因此,若要提高现有地震系数法的适应性,迫切需要对其进行修正。文中首先依据地震系数法进行抗震计算,分析其局限性;然后通过反应位移法[5-10]、动力时程法[11-14]的计算结果对地震系数法进行修正,提出在Ⅴ级围岩条件下, 不同洞径跨度采用地震系数法隧道上覆土柱合理计算高度,以供隧道工程抗震计算参考。
1 地震系数法现行的隧道抗震设计地震力计算方法有静力法和动力法两大类。静力法主要有:地震系数法、反应位移法、瑞利波法(浅埋隧道)、福氏法(深埋隧道)等。动力法可以考虑结构物及地层的非线性特性,模拟结构物和地层的相互作用,能够较好地反映隧道结构和围岩的地震响应特征,但动力法在计算模型和计算参数选择、地震波及其输入方式、边界条件确定等方面还需要进行更深入研究,而且其求解复杂,耗时大,目前在实际工程中广泛使用还存在困难。
地震系数法计算方法简单,计算工作量小,参数易于确定,目前在我国交通隧道规范中被采用,但需要对其进一步修正,提高适应性。
1.1 地震系数法计算理论当地震发生时,结构物受到一种惯性力的作用,这种由地震引起的惯性力称为地震力。结构物在进行抗震验算时,一般只计算水平地震力的作用。《铁路工程抗震设计规范》8.1.2规定隧道的地震作用应按设计地震采用静力法计算。地震力的作用系短暂的、偶然性的,按特殊荷载考虑。
地震引起的荷载只考虑水平地震力的作用,作用大小由水平地震系数确定。水平地震系数Kh及相应的地震角按表 1取值。
| 表 1 地震系数 |
水平地震力修正系数ηc岩石地基取0.20,非岩石地基取0.25。
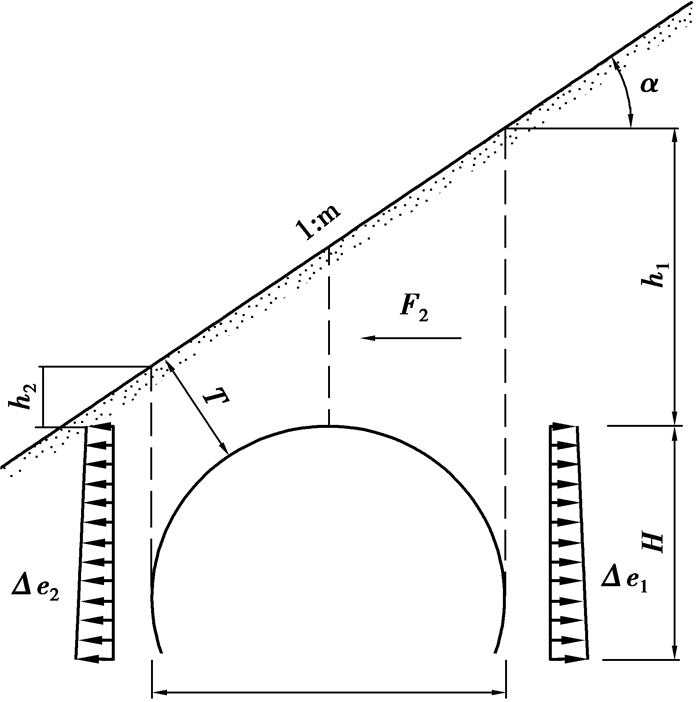
衬砌承受地震力主要由自重水平地震力、地震侧压力增量、上覆土柱水平地震力3部分组成。如图 1所示(图中只表示了地震时附加地震力部分)。
|
图 1 隧道地震引起的特殊荷载 |
该地震力是由于水平地震加速度引起的结构本身的惯性力,根据《铁路工程抗震设计规范》,作用于衬砌上任一质点的水平地震力,按式(1)计算。
| $ {F_{ihe}} = {\eta _c} \cdot {A_g} \cdot {m_i}。$ | (1) |
水平加速度大小为a=ηcKhg;各单元受自重惯性力F1=mia。其中:Kh为水平地震系数,按表 1选取;g为重力加速度;mi为衬砌单元质量。
1.1.2 侧向土压力增量| $ 内侧:{e_{1i}} = \gamma {h_i}\left( {{\lambda _1} - \lambda } \right) = \gamma {h_1}\Delta {\lambda _1}, $ | (2) |
| $ 外侧:{e_{2i}} = \gamma {h_i}^\prime \left( {{\lambda _2} - \lambda '} \right) = \gamma {h_2}\Delta {\lambda _2}, $ | (3) |
式中:λ、λ′为内、外侧非地震时侧压力系数;h1、h2为内、外侧拱顶水平至地面的高度;hi、h′i为内、外侧任一点i至地面的距离;γ为围岩重度;Δλ1、Δλ2为内、外侧侧压力系数增量;λ1、λ2为内、外侧地震时侧压力系数,分别按式(4)、(5)计算:
| $ \left. {\begin{array}{*{20}{l}} {{\lambda _1} = \frac{{\left( {{\rm{tg}}{\beta _1} - {\rm{tg}}{\varphi _1}} \right)\left( {1 - {\rm{tg}}{\theta _1}{\rm{tg}}\theta } \right)}}{{\left( {{\rm{tg}}{\beta _1} - {\rm{tg}}\alpha } \right)\left[ {1 + {\rm{tg}}{\beta _1}\left( {{\rm{tg}}{\varphi _1} - {\rm{tg}}{\theta _1}} \right) + {\rm{tg}}{\varphi _1}{\rm{tg}}{\theta _1}} \right]}}}\\ {{\lambda _2} = \frac{{\left( {{\rm{tg}}{\beta _2} - {\rm{tg}}{\varphi _2}} \right)\left( {1 - {\rm{tg}}{\theta _2}{\rm{tg}}\theta } \right)}}{{\left( {{\rm{tg}}{\beta _2}{\rm{ + tg}}\alpha } \right)\left[ {1 + {\rm{tg}}{\beta _2}\left( {{\rm{tg}}{\varphi _2} - {\rm{tg}}{\theta _2}} \right) + {\rm{tg}}{\varphi _2}{\rm{tg}}{\theta _2}} \right]}}} \end{array}} \right\}, $ | (4) |
| $ \left. {\begin{array}{*{20}{l}} {{\rm{tg}}{\beta _1} = {\rm{tg}}{\varphi _1} + \sqrt {\frac{{\left( {{\rm{t}}{{\rm{g}}^2}{\varphi _1} + 1} \right)\left( {{\rm{tg}}{\varphi _1} - {\rm{tg}}\alpha } \right)}}{{\left( {{\rm{tg}}{\varphi _1} - {\rm{tg}}{\theta _1}} \right)}}} }\\ {{\rm{tg}}{\beta _2} = {\rm{tg}}{\varphi _2} + \sqrt {\frac{{\left( {{\rm{t}}{{\rm{g}}^2}{\varphi _2} + 1} \right)\left( {{\rm{tg}}{\varphi _2}{\rm{ + tg}}\alpha } \right)}}{{\left( {{\rm{tg}}{\varphi _2} - {\rm{tg}}{\theta _2}} \right)}}} } \end{array}} \right\}, $ | (5) |
式中:φg为围岩计算摩擦角,(°);θ0为土柱两侧摩擦角,(°);α为地面坡度角,(°),当地面为平坡时α=0;β1、β2为内、外侧产生最大推力时的破裂角,(°);其中:φ1=φg-θ,φ2=φg+θ,θ1=θ0-θ,θ2=θ0+θ。
1.1.3 上覆土柱的水平地震力《铁路工程抗震设计规范》及《隧规》并未明确规定上覆土柱地震水平力计算方法,而根据《隧道手册》地震水平力的作用点于土柱质心。
上覆土柱垂直土压力大小由式(6)计算,分布图形与地面坡一致。
| $ P = \frac{\gamma }{2}\left[{\left( {{h_1} + {h_2}} \right)B-\left( {{\lambda _1}h_1^2 + {\lambda _2}h_2^2} \right){\rm{tg}}{\theta _0}} \right], $ | (6) |
式中B为坑道跨度,m。
则上覆土柱水平地震力
| $ {F_2} = {\eta _c}{K_h}P\;\;\left( {作用点为土柱质心} \right)。$ | (7) |
根据手册假定,F2作用点在土柱质心,那么洞顶土柱水平地震力将对衬砌有个弯矩作用效应,弯矩的大小为作用点到衬砌的距离H。
1.2 地震系数法计算及分析文中以某单线隧道140 km/h(隧道最大内净空跨度B为6.4 m)、双线隧道140 km/h(B为10.6 m)和双线隧道200 km/h(B为13.2 m)为例,采用地震系数法计算不同埋深情况下对应的衬砌弯矩最大值。在Ⅴ级围岩中,地震烈度为7度/8度时,对应水平地震动峰值加速度值为0.15 g/0.30 g。单线隧道140 km/h计算的埋深分别为0.5B、1B、1.5B和2B,双线隧道140 km/h计算的埋深分别为0.5B、1B和1.5B,双线隧道200 km/h计算的埋深分别为0.5B、1B和1.5B。3种断面的弯矩最值统计见表 2。不同断面型式衬砌的弯矩最大值随埋深的关系曲线如图 2所示。
| 表 2 不同断面型式和埋深下的控制弯矩值 |
|
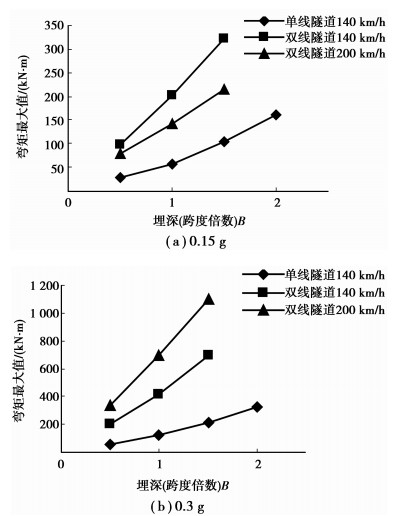
图 2 不同断面型式衬砌的弯矩与埋深的关系 |
从图 2可知,对相同断面的隧道结构,衬砌弯矩最大值随着埋深的增加而增大;对不同跨度的隧道结构,衬砌弯矩最大值随着跨度的增加而增大。这是因为根据地震系数法,上覆土柱的惯性力作用随埋深和跨度的增加而变大,所以衬砌的弯矩响应也随之变大。在一定的埋深时,采用地震系数法进行抗震计算的结果与实际工程一致。当隧道埋深增加到一定程度后,地震系数法计算地震作用下的衬砌弯矩峰值急剧增大,这与工程实际情况不相符合,且与地下结构的地震响应机理也不符,地下结构物是随着地层而振动,其埋深越大,地震震害越轻。文中基于地震系数法的这一局限性进行研究,以期获得地震系数法上覆土柱合理计算高度,提高现有地震系数法的适应性。
2 地震系数法的修正在Ⅴ级围岩、输入水平地震加速度峰值为0.15 g/0.3 g的条件下,分别对单线140 km/h(B=6.4 m)、双线140 km/h(B=10.6 m)和双线200 km/h(B=13.2 m)3种断面的隧道型式采用地震系数法、反应位移法和动力时程法进行不同埋深下的抗震计算,并对3种方法的计算结果进行比较分析。长期实践证明:动力时程分析能很好地处理介质中的非均匀性、各向异性、非线性及复杂几何边界条件,得到地层和结构在地震全时段的内力和位移反应,较好地揭示隧道在地震荷载作用下的反应规律。但由于动力时程分析复杂且求解代价很大,工程实际应用中广泛推广还有困难。反应位移法和动力时程法的弯矩最大值计算结果在趋势上保持一致,量值上也比较接近,而且通过振动台模型试验也验证了该结论(限于篇幅,未涉及振动台试验部分,可参见另文)。鉴于此,通过反应位移法和动力时程法的计算结果对地震系数法的计算埋深进行合理修正,提出Ⅴ级围岩条件下,隧道采用地震系数法的上覆土柱合理计算高度。
2.1 水平地震动峰值加速度值0.15 g 2.1.1 单线140 km/h隧道在输入地震动水平加速度峰值为0.15 g时,对Ⅴ级围岩中的单线140 km/h分别采用地震系数法、反应位移法和动力时程法在不同埋深条件下进行抗震计算,并对计算的弯矩结果进行统计,3种方法计算结果的比较分析如图 3所示。
|
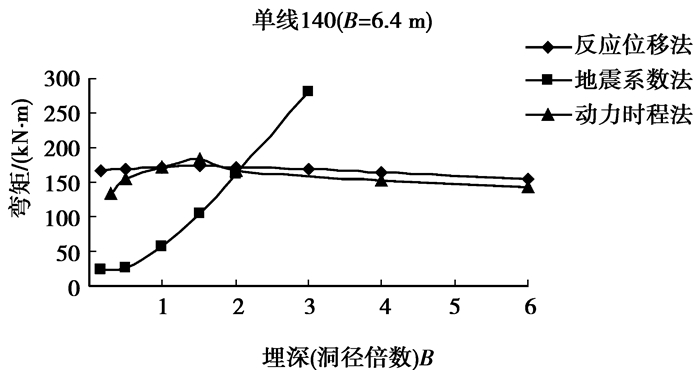
图 3 单线140 km/h隧道弯矩与埋深的关系曲线 |
从图 3可以看出:在Ⅴ级围岩、地震动水平加速度峰值为0.15 g条件下,对于单线140 km/h隧道,当埋深约为2B时,地震系数法、反应位移法和动力时程法计算的衬砌弯矩最大值结果非常接近。埋深超过2B后,地震系数法计算的弯矩最大值随埋深的加大急剧增大,与工程实际、地震响应特征和震害现象都不符合;但在埋深小于2B工况下,地震系数法的结果又偏小,这也可能是过去一直沿用地震系数法进行隧道抗震设防,在洞口等埋深较浅的位置发生震害较多的原因之一。而反应位移法与动力时程法的计算弯矩最大值随埋深的变化趋势一致,且数值非常接近。基于此,用反应位移法和动力时程法的计算结果对隧道内净空跨度B≤8 m时地震系数法上覆土柱地震作用的计算高度进行修正,取2B为其计算高度。
2.1.2 双线140 km/h隧道在输入地震动水平加速度峰值为0.15 g时,对Ⅴ级围岩中的双线140 km/h分别采用地震系数法、反应位移法和动力时程法在不同埋深条件下进行抗震计算,并对计算的弯矩结果进行统计,3种方法计算结果的比较分析如图 4所示。
|
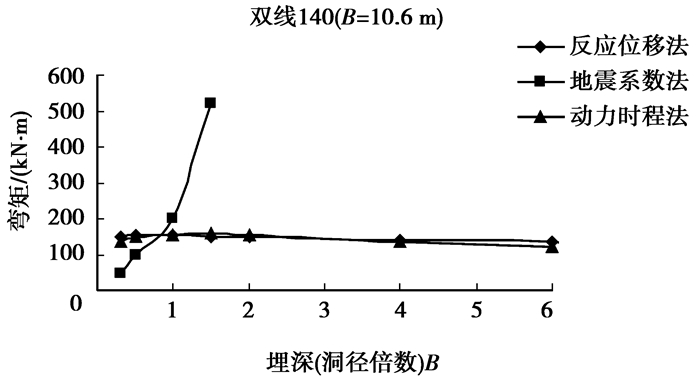
图 4 双线140 km/h隧道弯矩与埋深的关系曲线 |
从图 4可以看出:在Ⅴ级围岩、地震动水平加速度峰值为0.15 g条件下,对于双线140 km/h隧道,当埋深约为1B时,地震系数法、反应位移法和动力时程法计算的衬砌弯矩最大值结果非常接近。埋深超过1B后,地震系数法计算的弯矩最大值随埋深的加大急剧增大,但在埋深小于1B工况下,地震系数法的结果又偏小,而反应位移法与动力时程法的计算弯矩最大值随埋深的变化趋势一致,且数值非常接近。基于此,用反应位移法和动力时程法的计算结果对隧道内净空跨度8 m<B≤12 m时地震系数法上覆土柱地震作用的计算高度进行修正,取1B为其计算高度。
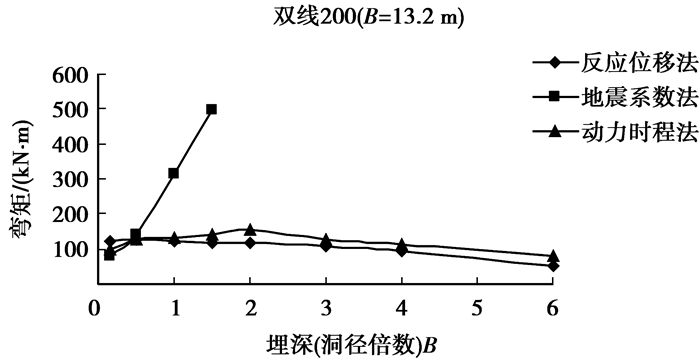
2.1.3 双线200 km/h隧道在输入地震动水平加速度峰值为0.15 g时,对Ⅴ级围岩中的双线200 km/h分别采用地震系数法、反应位移法和动力时程法在不同埋深条件下进行抗震计算,并对计算的弯矩结果进行统计,3种方法计算结果的比较分析如图 5所示。
|
图 5 双线200 km/h隧道弯矩与埋深的关系曲线 |
从图 5可以看出:在Ⅴ级围岩、地震动水平加速度峰值为0.15 g条件下,对于双线200 km/h隧道,当埋深约为0.5B时,地震系数法、反应位移法和动力时程法计算的衬砌弯矩最大值结果非常接近。埋深超过0.5B后,地震系数法计算的弯矩最大值随埋深的加大急剧增大,但在埋深小于0.5B工况下,地震系数法的结果又偏小。而反应位移法与动力时程法的计算弯矩最大值随埋深的变化趋势一致,且数值非常接近。基于此,用反应位移法和动力时程法的计算结果对隧道内净空跨度B>12 m时地震系数法上覆土柱地震作用的计算高度进行修正,取0.5B为其计算高度。
2.2 水平地震动峰值加速度值0.3 g在输入地震动水平加速度峰值为0.3 g时,对Ⅴ级围岩中的单线140 km/h、双线140 km/h和双线200 km/h分别采用地震系数法、反应位移法和动力时程法在不同埋深条件下进行抗震计算,并对计算的弯矩结果进行统计,3种方法计算结果的比较分析如图 6~8所示。
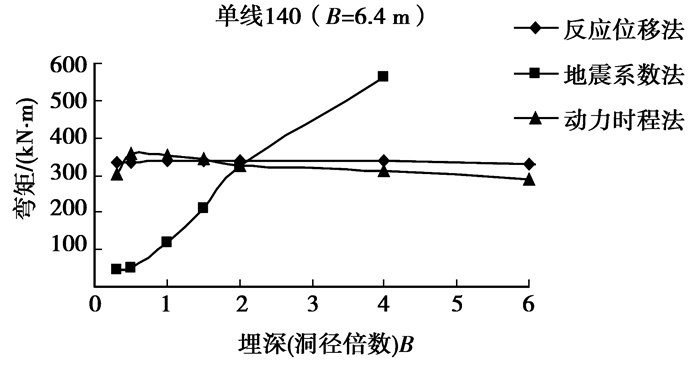
|
图 6 单线140 km/h隧道弯矩与埋深的关系曲线 |
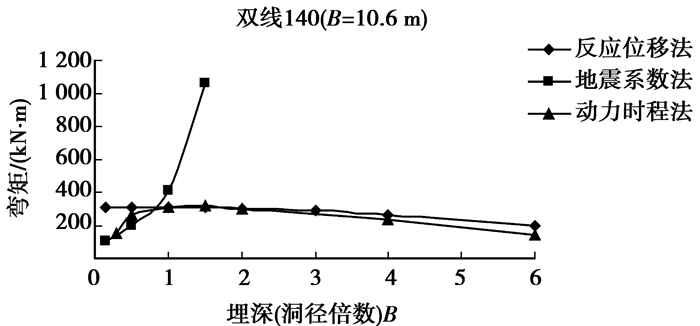
|
图 7 双线140 km/h隧道弯矩与埋深的关系曲线 |
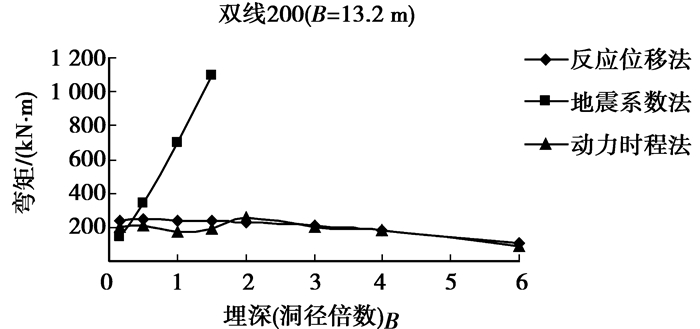
|
图 8 双线200 km/h隧道弯矩与埋深的关系曲线 |
从图 6~图 8可以看出:当Ⅴ级围岩、水平地震动峰值加速度为0.3 g时,对于单线140 km/h(B=6.4 m)、双线140 km/h(B=10.6 m)和双线200 km/h(B=13.2 m)隧道,反应位移法和动力时程法计算的衬砌弯矩最大值非常接近,随埋深的变化规律一致,而地震系数法分别约在埋深2.0B、0.8B及0.4B后出现弯矩急剧增大。
3 结论在不同地震动水平加速度峰值的情况下,地震系数法、反应位移法和动力时程法所得衬砌弯矩值分布规律大致相同,并不影响修正地震系数法上覆土柱地震作用的计算控制高度,因此埋深的选取与地震动水平加速度峰值无关(地震动水平峰值加速度为0.2 g和0.4 g的计算结果以及振动台实验结果所呈现的规律相似,由于篇幅所限,不再赘述)。
通过以上比较分析,同时考虑安全性的影响及实际工程的特征,可在此基础上乘以一定的安全系数,作为Ⅴ级围岩不同跨度条件下地震系数法上覆土柱地震作用的计算控制高度。按照《铁路工程抗震设计规范》的分类,隧道处于Ⅴ级围岩条件下,隧道衬砌的内净空最大跨度B≤8 m时,计算埋深取2.0B;8 m<B≤12 m时,计算埋深取1.0B;B>12 m时,计算埋深取0.5B。
| [1] | 钱七虎, 何川, 晏启祥. 隧道工程动力响应特性与汶川地震隧道震害分析及启示[C]//中国岩石力学与工程学会. 汶川大地震工程震害调查分析与研究论文集. 北京: 科学出版社, 2009: 633-643. |
| [2] | 中国人民共和国交通部. JTJ 004-89公路工程抗震设计规范[S]. 北京: 人民交通出版社, 1989. |
| [3] |
刘晶波, 李彬, 谷音.
地铁盾构隧道地震反应分析[J]. 清华大学学报:自然科学版, 2005, 45(6): 757–760.
LIU Jingbo, LI Bin, GU Yin. Seismic response analysis of shielded subway tunnels[J]. Journal of Tsinghua University:Science and Technology, 2005, 45(6): 757–760. (in Chinese) |
| [4] |
郑永来, 杨林德.
地下结构震害与抗震对策[J]. 工程抗震, 1999(4): 23–28.
ZHENG Yonglai, YANG Linde. Earthquake damage and resistant measure of underground structures[J]. Earthquake Resistant Engineering, 1999(4): 23–28. (in Chinese) |
| [5] |
黄先锋.
地下结构的抗震计算:位移响应法[J]. 铁道建筑, 1999(6): 3–6.
HUANG Xianfeng. Seismic calculation of underground structure, the displacement response method[J]. Railway Engineering, 1999(6): 3–6. (in Chinese) |
| [6] |
边金, 陶连金, 张印涛, 等.
地下结构抗震设计方法的比较与分析[J]. 现代隧道技术, 2008, 45(6): 50–55.
BIAN Jin, TAO Lianjin, ZHANG Yintao, et al. Comparison and analysis of the aseismic design methods for underground structures[J]. Modern Tunneling Technology, 2008, 45(6): 50–55. (in Chinese) |
| [7] |
刘如山, 胡少卿, 石宏彬.
地下结构抗震计算中拟静力法的地震荷载施加方法研究[J]. 岩土工程学报, 2007, 29(2): 237–242.
LIU Rushan, HU Shaoqing, SHI Hongbin. Study on seismic loading of pseudo-static approach used in the seismic design of underground structure[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(2): 237–242. (in Chinese) |
| [8] | 国家地震局. GB 50267-97核电厂抗震设计规范[S]. 北京: 中国计划出版社, 1997. |
| [9] | Kawamata K. Seismic design of underground structure[M]. Tokyo: Kajima Press, 1994. |
| [10] |
吕和林.
一种用于浅埋隧道抗震分析的拟静力数值方法[J]. 西南交通大学学报, 1999, 34(3): 315–319.
Lü Helin. A mimetic statics numeric method on earthquake resistance analysis of shallow buried tunnels[J]. Journal of Southwest Jiaotong University, 1999, 34(3): 315–319. (in Chinese) |
| [11] |
耿萍, 何川, 晏启祥.
盾构隧道纵向地震响应分析[J]. 西南交通大学学报, 2007, 42(3): 283–287.
GENG Ping, HE Chuan, YAN Qixiang. Analysis of longitudinal seismic response of shield tunnel[J]. Journal of Southwest Jiaotong University, 2007, 42(3): 283–287. (in Chinese) |
| [12] |
庄海洋, 陈国兴.
软弱地基浅埋地铁区间隧洞的地震反应分析[J]. 岩石力学与工程学报, 2005, 24(14): 2506–2512.
ZHUANG Haiyang, CHEN Guoxing. Earthquake response of shallow subway tunnels in soft foundation[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(14): 2506–2512. DOI:10.3321/j.issn:1000-6915.2005.14.016 (in Chinese) |
| [13] |
潘昌实.
隧道及地下结构物抗震问题的研究概况[J]. 现代隧道技术, 1996(5): 7–16.
PAN Changshi. Researches on aseismic besign of tunnels and underground structures[J]. Modern Tunnelling Technology, 1996(5): 7–16. (in Chinese) |
 2013, Vol. 36
2013, Vol. 36

