重庆大学 机械传动国家重点实验室, 重庆 400044
收稿日期: 2012-12-15
基金项目: 国家自然科学基金资助项目(51275541);机械传动国家重点实验室自主项目资助(SKLMT-ZZKT-2012 ZD06);中央高校基本科研业务费资助(CDJZR12280011)
作者简介:
王艳阳(1980-), 女, 重庆大学博士研究生, 主要从事车辆电磁悬架系统的研究。
Energy conversion analysis of vehicle electromagnetic suspension using power flow method
The State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, China
车辆行驶时,车轴与簧载质量之间的振动能量,在传统阻尼作用下以热能的形式耗散。一方面,这种热能的耗散影响了器件的工作性能和使用寿命;另一方面,在能源短缺的环境下这种能量耗散也是一种浪费。因此,为了回收车轴与簧载质量间的振动能量,馈能型悬架的研究应运而生[1-6]。电磁主动悬架作为一种高效的馈能型悬架与被动悬架、半主动悬架和液气压主动悬架相比具有作动频率宽、控制精度高和能量可回收等优点,得到了国内外学者的关注。
日本学者Suda等[7-8]研究了一种自供能主动电磁悬架系统。该系统把车辆动力学性能和电磁悬架的自供能特性进行了折中。在车辆动力学性能略做牺牲的前提下,实现了电磁悬架能量需求和能量反馈的平衡。Yu等[9]提出了一种电磁主动悬架的鲁棒控制,该控制采用内环和外环的控制结构。外环计算变参数情况下,电磁主动悬架所期望的控制力;内环通过控制电磁主动悬架的电流,跟踪所期望的控制力。荷兰学者Paulides研究组[10-12]针对电磁悬架系统设计了二次型调节控制器,在提高车辆乘坐舒适性,降低轮胎动载荷的同时分析了电磁悬架无场阻尼值对悬架馈能特性的影响。邓兆祥等[13]设计了一种具有行程大、推力大及响应快速等特点的新型电磁作动器。分析了电磁力与气隙密度、电源电压和频率等参数的关系。David等[14]提出了一种基于电磁悬架的车辆动力学性能和节能特性的双目标控制结构。根据不同的控制目标确定电磁悬架的工作模式:主动模式、被动模式和半主动模式,以期实现车辆动力学性能和节能特性的平衡。喻凡等[15]对近年来馈能型主动悬架的发展和研究进行了全面回顾和总结,重点分析了馈能式电磁悬架的核心问题,指出量化和提高馈能效率是馈能式悬架的核心问题之一。然而在上述研究中,电磁悬架能量转换和馈能效率的计算基准不尽相同。文献[1, 2, 14]仅考虑了悬架系统内部的能量转换和消耗;而文献[5, 10]则把悬架馈能功率与整车功率进行比较计算。电磁悬架能量转换量和转换率缺少统一的量化方法,而对于馈能悬架的最大馈能潜力更少有文献涉及。
笔者采用功率流的方法,分析了电磁悬架的馈能特性。给出了馈能式电磁悬架的能量转换量及转换率的量化方法。解决了馈能式电磁悬架系统的能量量化问题。通过对比分析馈能式主动电磁悬架系统、馈能式被动电磁悬架系统和最大馈能系统的馈能特性,得出了馈能式主动悬架系统和馈能式被动悬架系统的馈能特点,同时评估了悬架系统的最大馈能潜力。为车辆的乘坐舒适性、操纵稳定性和节能性的综合控制提供了理论基础。
1 馈能式电磁悬架模型
1.1 1/4悬架模型
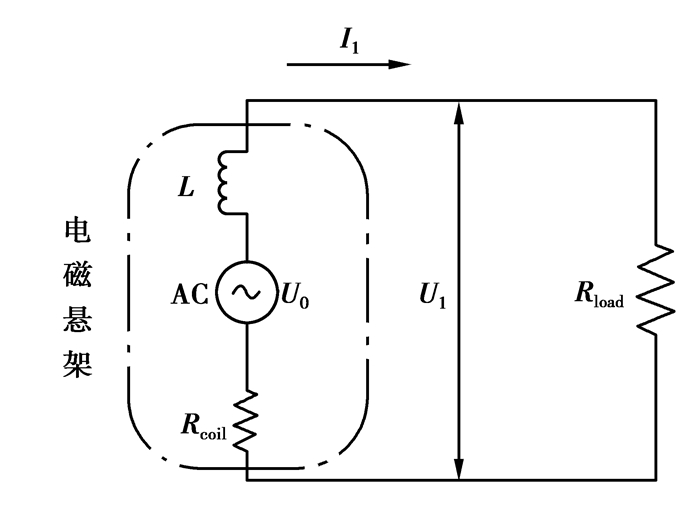
图 1为1/4馈能式电磁悬架模型。其中虚线框内为电磁减振器的等效电路。L、AC和Rcoil分别为减振器的等效电感、等效电源和等效电阻。
当路面激励传递给非簧载质量时,簧载质量和非簧载质量之间发生相对运动。电磁悬架将这部分振动转变为线圈与磁场间的相对运动。根据法拉利定律,闭合线圈中的磁场强度发生变化时,线圈内将产生感应电压U0和电磁反力Fem。当|U0|≤U1时,外部电路向电磁减振器提供电能;U0>U1时,电磁减振器向超级电容正向充电;当U0<-U1时,电磁减振器向超级电容反向充电。根据牛顿定律,可得二自由度馈能式悬架系统的运动微分方程为
|
$
\left\{ \begin{array}{l}
{m_{\rm{s}}}{{\ddot z}_{\rm{s}}} = - {d_{\rm{p}}}\left( {{{\dot z}_{\rm{s}}} - {{\dot z}_{\rm{u}}}} \right) - {k_{\rm{s}}}\left( {{z_{\rm{s}}} - {z_{\rm{u}}}} \right) - {F_{{\rm{em}}}},\\
{m_{\rm{u}}}{{\ddot z}_{\rm{u}}} = {d_{\rm{p}}}\left( {{{\dot z}_{\rm{s}}} - {{\dot z}_{\rm{u}}}} \right) + {k_{\rm{s}}}\left( {{z_{\rm{s}}} - {z_{\rm{u}}}} \right),\\
- {k_t}\left( {{z_{\rm{u}}} - q} \right) + {F_{{\rm{em}}}}。\end{array} \right.
$
|
(1) |
式中:ms为簧载质量;mu为非簧载质量;zs为簧载质量位移;zu为非簧载质量位移;q为路面位移激励;ks为悬架弹簧等效刚度;kt为轮胎等效刚度;dp为电磁作动器等效无场阻尼;Fem为电磁悬架作动力。
电磁减振器所提供的阻尼力为
|
$
{F_{{\rm{em}}}} = K{I_1},
$
|
(2) |
式中:K为减振器常数;I1为减振器电流。
1.2 馈能电路模型
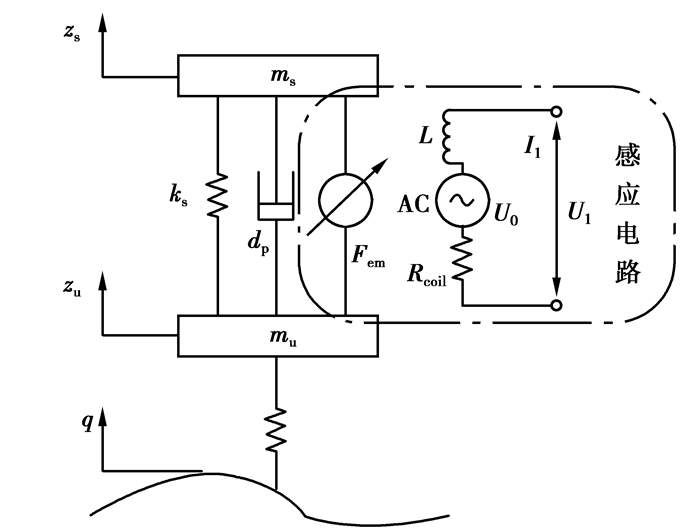
图 2为电磁减振器作为发电机的馈能电路模型。Rvar为可变电阻,通过调整Rvar可以控制流过减振器的电流,从而改变减振器所产生的阻尼力。
二极管D把减振器产生的交流电转换为直流电给电容充电,因此有I2=|I1|。电磁悬架产生的感应电压U0为
x为簧载质量与非簧载质量相对速度,即
|
$
x = {{\dot z}_{\rm{s}}} - {{\dot z}_{\rm{u}}}。$
|
(4) |
根据基尔霍夫定律可得
|
$
{U_0} = L{{\dot I}_1} + \left( {{R_{{\rm{coil}}}} + {R_{{\mathop{\rm var}} }}} \right){I_1} + 2{V_{\rm{F}}} + {U_{\rm{c}}},
$
|
(5) |
式中:VF为二极管两端压降;Uc为电容两端电压。
电磁减振器两端的电压为
|
$
{U_1} = {U_{{\mathop{\rm var}} }} + 2{V_{\rm{F}}} + {U_{\rm{c}}}。$
|
(6) |
由于电磁减振器的电感相对较小,因此在电路中忽略电感对馈能电路的影响。由公式(3)~(6)可得减振器作为发电机时,流过减振器的电流为
|
$
{I_1} = \left\{ \begin{array}{l}
0,\left| {{U_0}} \right| \le {U_1};\\
\left( {K\dot x - 2{V_{\rm{F}}} - {U_{\rm{c}}}} \right)/\left( {{R_{{\rm{coil}}}} + {R_{{\mathop{\rm var}} }}} \right),{U_0} > {U_1};\\
\left( {K\dot x + 2{V_{\rm{F}}} + {U_{\rm{c}}}} \right)/\left( {{R_{{\rm{coil}}}} + {R_{{\mathop{\rm var}} }}} \right),{U_0} < - {U_1}。\end{array} \right.
$
|
(7) |
由公式(7)可得
|
$
{R_{{\mathop{\rm var}} }} = \left\{ \begin{array}{l}
0,\left| {{U_0}} \right| \le {U_1};\\
\left( {K\dot x - 2{V_{\rm{F}}} - {U_{\rm{c}}} - {I_1}{R_{{\rm{coil}}}}} \right)/{I_1},{U_0} > {U_1};\\
\left( {K\dot x + 2{V_{\rm{F}}} + {U_{\rm{c}}} - {I_1}{R_{{\rm{coil}}}}} \right)/{I_1},{U_0} < - {U_1}。\end{array} \right.
$
|
(8) |
1.3 放电电路模型
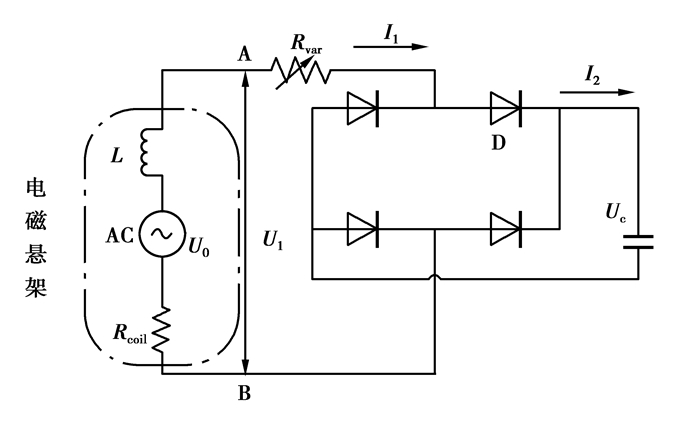
图 3为电磁减振器作为电动机的电路模型。流过减振器的电流为
|
$
{I_1} = \left\{ \begin{array}{l}
\left( {{U_1} - {U_0}} \right)/{R_{{\rm{coil}}}},\left| {{U_0}} \right| \le {U_1};\\
0,{U_0} > {U_1};\\
0,{U_0} < - {U_1}。\end{array} \right.
$
|
(9) |
1.4 最大馈能电路模型
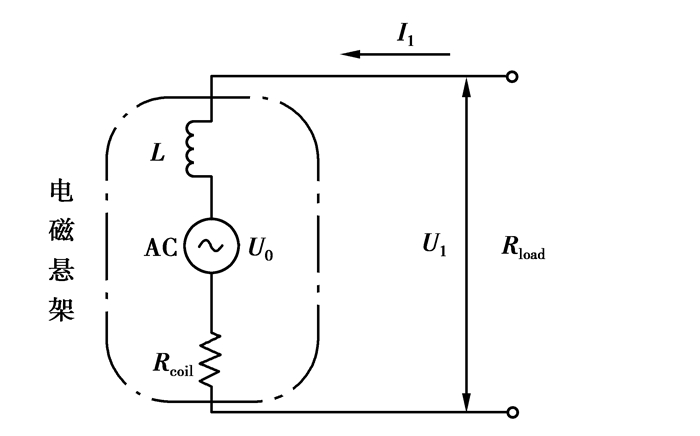
为了研究馈能式悬架系统的最大馈能潜力,根据阻抗匹配原理设计了最大馈能电路,其等效电路如图 4所示。
当减振器的外部负载Rload等于内部电阻Rload时,系统输出的功率Pout最大。流过减振器的电流为
|
$
{I_1} = K\dot x/\left( {{R_{{\rm{coil}}}} + {R_{{\rm{load}}}}} \right)。$
|
(10) |
2 馈能式电磁悬架功率流分析
2.1 功率流分析
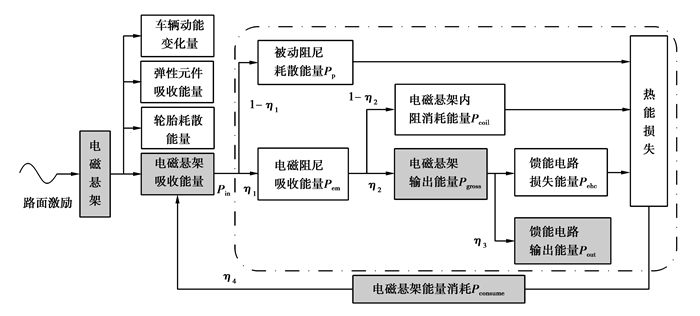
图 5为馈能式电磁悬架功率流图。根据能量守恒定律,由路面激励输入给车体的能量主要转换为4种形式:车体动能的变化量、轮胎耗散的能量、弹性元件吸收的能量和车辆悬架阻尼损失的能量Pin。
车辆安装馈能式电磁悬架后,Pin一部分被电磁悬架的无场阻尼消耗掉Pp;另一部分被电磁阻尼吸收Pem。Pem的一部分能量通过电磁减振器的内阻以热能形式耗散Pcoil;其余的能量输出给馈能电路Pgross。而Pgross的能量一部分被馈能电路损耗掉Pehc,其余的能量输出给超级电容存储Pout。当电磁减振器工作在电动机的状态时,Pout可以为之供电。据能量守恒定律得
|
$
\begin{array}{l}
{P_{{\rm{in}}}} = {P_{\rm{p}}} + {P_{{\rm{em}}}} = \\
\;\;\;\;\;\;\;\;{P_{\rm{p}}} + {P_{{\rm{coil}}}} + {P_{{\rm{gross}}}} = \\
\;\;\;\;\;\;\;\;{P_{\rm{p}}} + {P_{{\rm{coil}}}} + {P_{{\rm{ehc}}}} + {P_{{\rm{out}}}}。\end{array}
$
|
(11) |
2.2 各部分能量转换量及转换率
当馈能式减振器工作在发电机的状态,各部分功率为
|
$
{P_{{\rm{em}}}} = {F_{{\rm{em}}}}\dot x,
$
|
(12) |
|
$
{P_{\rm{p}}} = {d_{\rm{p}}}{{\dot x}^2},
$
|
(13) |
|
$
{P_{{\rm{coil}}}} = I_1^2{R_{{\rm{coil}}}},
$
|
(14) |
|
$
{P_{{\rm{ehc}}}} = 2{V_{\rm{F}}}\left| {{I_1}} \right| + I_1^2{R_{{\mathop{\rm var}} }},
$
|
(15) |
|
$
{P_{{\rm{out}}}} = {U_{\rm{c}}}\left| {{I_1}} \right|,
$
|
(16) |
|
$
{{\bar P}_{\rm{p}}} = \frac{1}{{{t_2} - {t_1}}}\int\limits_{{t_1}}^{{t_2}} {{P_{\rm{p}}}{\rm{d}}t} ,
$
|
(17) |
|
$
{{\bar P}_{{\rm{em}}}} = \frac{1}{{{t_2} - {t_1}}}\int\limits_{{t_1}}^{{t_2}} {{P_{{\rm{em}}}}{\rm{d}}t} ,
$
|
(18) |
|
$
{{\bar P}_{{\rm{ehc}}}} = \frac{1}{{{t_2} - {t_1}}}\int\limits_{{t_1}}^{{t_2}} {{P_{{\rm{ehc}}}}{\rm{d}}t} ,
$
|
(19) |
|
$
{{\bar P}_{{\rm{out}}}} = \frac{1}{{{t_2} - {t_1}}}\int\limits_{{t_1}}^{{t_2}} {{P_{{\rm{out}}}}{\rm{d}}t} 。$
|
(20) |
各部分能量转换率为
|
$
{\eta _1} = \frac{{{{\bar P}_{{\rm{em}}}}}}{{{{\bar P}_{{\rm{in}}}}}} = \frac{{{{\bar P}_{{\rm{em}}}}}}{{{{\bar P}_{{\rm{em}}}} + {{\bar P}_P}}},
$
|
(21) |
|
$
{\eta _2} = \frac{{{{\bar P}_{{\rm{gross}}}}}}{{{{\bar P}_{{\rm{em}}}}}} = \frac{{{{\bar P}_{{\rm{ehc}}}} + {{\bar P}_{{\rm{out}}}}}}{{{{\bar P}_{{\rm{em}}}}}},
$
|
(22) |
|
$
{\eta _3} = \frac{{{{\bar P}_{{\rm{out}}}}}}{{{{\bar P}_{{\rm{gross}}}}}} = \frac{{{{\bar P}_{{\rm{out}}}}}}{{{{\bar P}_{{\rm{out}}}} + {{\bar P}_{{\rm{ehc}}}}}},
$
|
(23) |
|
$
\eta = \frac{{{{\bar P}_{{\rm{out}}}}}}{{{{\bar P}_{{\rm{in}}}}}} = {\eta _1} \cdot {\eta _2} \cdot {\eta _3}。$
|
(24) |
当减振器工作在电动机状态,减振器消耗的功率为
|
$
{P_{{\rm{consume}}}} = I_1^2{R_{{\rm{coil}}}} + {U_0}{I_1},
$
|
(25) |
|
$
{{\bar P}_{{\rm{consume}}}} = \frac{1}{{{t_2} - {t_1}}}\int\limits_{{t_1}}^{{t_2}} {{P_{counsume}}{\rm{d}}t} ,
$
|
(26) |
|
$
{\eta _4} = \frac{{{{\bar P}_{{\rm{consume}}}}}}{{{{\bar P}_{{\rm{in}}}}}}。$
|
(27) |
当减振器工作在最大馈能状态,各部分功率转换量及转换率为
|
$
{P_{\rm{p}}} = {d_{\rm{p}}}{{\dot x}^2},
$
|
(28) |
|
$
\begin{array}{l}
{P_{{\rm{em}}}} = U_0^2/\left( {{R_{{\rm{coil}}}} + {R_{{\rm{load}}}}} \right) = \\
\;\;\;\;\;\;\;\;\;{\left( {K\dot x} \right)^2}/\left( {2{R_{{\rm{coil}}}}} \right),
\end{array}
$
|
(29) |
|
$
{P_{{\rm{coil}}}} = U_0^2/{R_{{\rm{coil}}}} = {\left( {K\dot x} \right)^2}/{R_{{\rm{coil}}}},
$
|
(30) |
|
$
{P_{{\rm{out}}}} = I_1^2{R_{{\rm{load}}}},
$
|
(31) |
|
$
{\eta _1} = \frac{{{{\bar P}_{{\rm{em}}}}}}{{{{\bar P}_{{\rm{in}}}}}} = 1 - \frac{{2{d_{\rm{p}}}{R_{{\rm{coil}}}}}}{{{K^2} + 2{d_{\rm{p}}}{R_{{\rm{coil}}}}}},
$
|
(32) |
|
$
{\eta _2} = \frac{{{{\bar P}_{{\rm{gross}}}}}}{{{{\bar P}_{{\rm{em}}}}}} = \frac{{{{\bar P}_{{\rm{out}}}}}}{{{{\bar P}_{{\rm{em}}}}}} = \frac{{{R_{{\rm{coil}}}}}}{{2{R_{{\rm{coil}}}}}} = 0.5,
$
|
(33) |
|
$
{\eta _3} = \frac{{{{\bar P}_{{\rm{out}}}}}}{{{{\bar P}_{{\rm{gross}}}}}} = \frac{{{{\bar P}_{{\rm{out}}}}}}{{{{\bar P}_{{\rm{out}}}}}} = 100,
$
|
(34) |
|
$
\eta = \frac{{{{\bar P}_{{\rm{out}}}}}}{{{{\bar P}_{{\rm{in}}}}}} = {\eta _1} \cdot {\eta _2} \cdot {\eta _3}。$
|
(35) |
3 仿真及结果分析
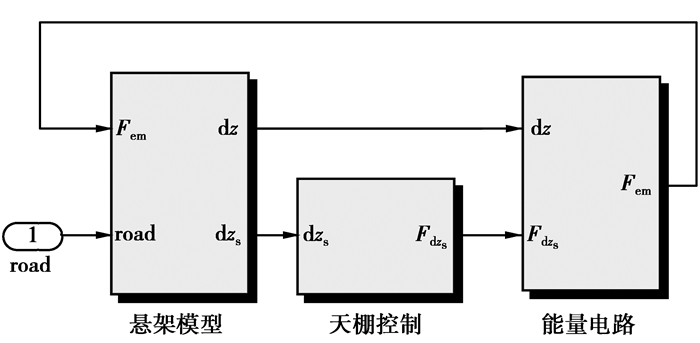
为了研究馈能式电磁悬架的馈能规律,设计了馈能式被动系统、馈能式主动系统和最大馈能系统。图 6为馈能式主动系统,其控制器采用了天棚控制。
天棚控制器根据车辆的状态计算期望的控制力及其控制电阻值;馈能电路调整控制电阻,使减振器跟踪期望的控制力,对车辆进行控制。仿真在保证车辆舒适性和稳定性的基础上,对车辆的馈能特性进行了分析。表 1为馈能式电磁悬架参数。仿真车速为80 km/h,取C级路面输入。
表 1(Table 1)
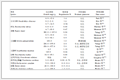
表 1 馈能式悬架模型参数
| 名称 |
符号 |
单位 |
名义值 |
| 簧载质量 |
ms |
kg |
250 |
| 非簧载质量 |
mu |
kg |
40 |
| 悬架刚度 |
ks |
N/m |
19 600 |
| 轮胎刚度 |
kt |
N/m |
309 511 |
| 悬架等效阻尼 |
dp |
N·s/m |
1 600 |
| 电机常数 |
K |
N/A |
115 |
| 电容 |
C |
F |
10 |
|
表 1 馈能式悬架模型参数
|
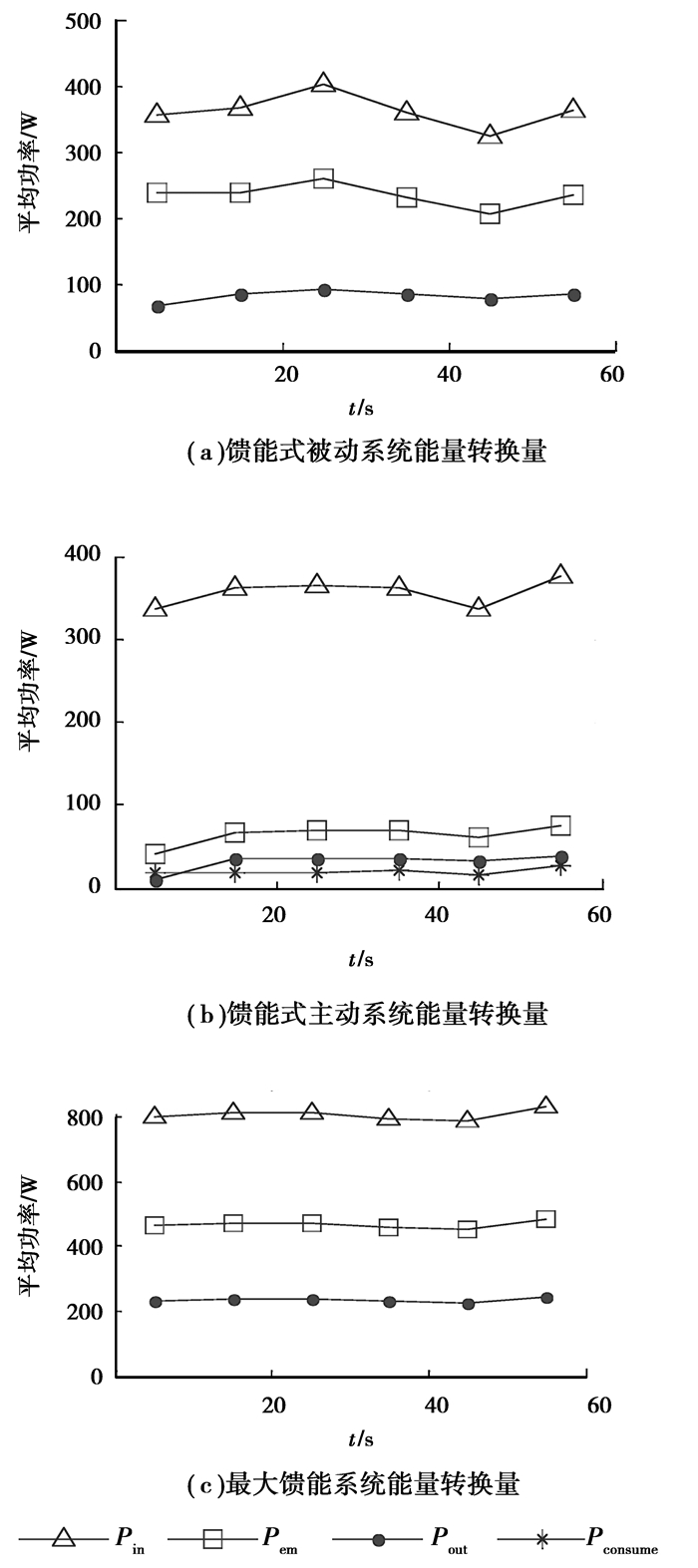
由图 7可以看出各部分能量转换量在时间历程上呈现出非线性特性。这主要是由于路面激励的非线性造成的。比较图 7(a)、(b)和(c)可知,馈能式被动系统、馈能式主动系统和最大馈能系统的输出量分别约为100、40和200 W。这表明馈能式主动系统的馈能能力小于被动系统,并且主动系统和被动系统的馈能量皆小于最大馈能式系统,二者还有很大的改进空间。
由图 7(a)和(b)可以看出,馈能式被动系统和主动系统在工作前10 s,各项转换量偏低。在大约10 s以前,馈能式主动系统的输出能量Pout约为10 W,而能量需求量Pconsume约为20 W,系统输出的能量无法满足系统需要。然而在系统工作10 s以后,Pout升高至约40 W。这主要是由于馈能系统开始启动时,电容电压低于其额定电压,使其充电能力降低。随着馈能时间的延长,电容电压逐渐升高,系统的充电能力加强。从总体上来讲,主动馈能系统输出的能量可以满足系统的需要,系统可以实现自供能。
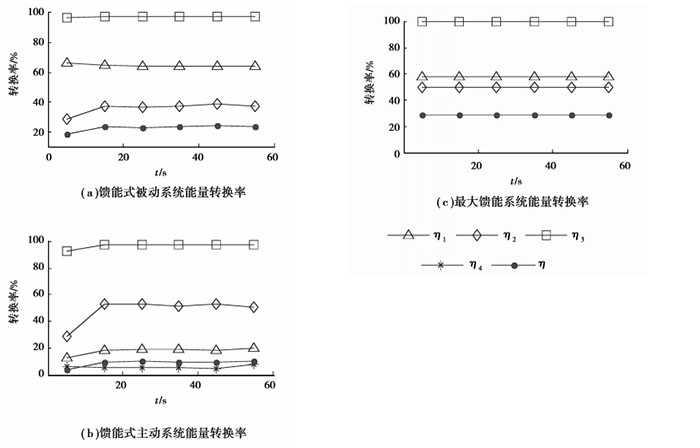
图 8为馈能式被动系统、馈能式主动系统和最大馈能系统的能量转换率。由图 8可见,馈能式主动系统和馈能式被动系统的能量转换率在时间历程上呈现出非线性特性,而最大馈能系统的各部分能量转换量呈现出线性特性。这一结论与公式(21)~(24),公式(27)和公式(32)~ (35)相一致。
表 2列出了在B、C级路面下,馈能式悬架的能量转换。由表 2可知,在B级路面下各部分能量转换量显著小于C级路面,然而二者的能量转换率差别相对较小。这表明馈能式电磁悬架系统的馈能量受路面激励的影响较为显著;而馈能率主要由系统内部结构决定,外在激励对馈能率的影响相对较小。
表 2(Table 2)

表 2 能量转换量及转换率
| 路面 |
模式 |
Pin/W |
Pem/W |
Pout/W |
Pconsume/W |
η1/% |
η2/% |
η3/% |
η4/% |
η/% |
| B |
主动 |
90.24 |
17.08 |
10.09 |
6.38 |
18.77 |
56.84 |
91.60 |
7.02 |
10.99 |
| 被动 |
122.27 |
77.58 |
40.01 |
0 |
63.57 |
52.57 |
97.02 |
0 |
32.35 |
| 最大 |
204.23 |
118.33 |
59.16 |
0 |
57.94 |
50.00 |
100.00 |
0 |
28.97 |
| C |
主动 |
356.38 |
63.75 |
30.79 |
20.19 |
17.81 |
48.36 |
96.73 |
5.64 |
8.57 |
| 被动 |
369.55 |
233.57 |
81.28 |
0 |
64.58 |
35.78 |
97.38 |
0 |
22.49 |
| 最大 |
816.95 |
473.35 |
236.67 |
0 |
57.94 |
50.00 |
100.00 |
0 |
28.97 |
|
表 2 能量转换量及转换率
|
在馈能式主动系统中,C级路面下的输出能量Pout为30.79 W,消耗的能量Pconsume为20.19 W,系统除了自供能以外,可以储存的能量为10.6 W;而被动系统可以存储的能量为81.28 W。结果表明,馈能式主动系统的馈能能力要小于被动系统。分析B级路面下的相关数据,可以得到同样的结论。
4 结论
1) 采用功率流的方法对馈能式电磁悬架的馈能特性进行了分析。给出了各项能量转换量和转换率的计算方法。解决了馈能式电磁悬架的能量量化问题。
2) 比较分析了馈能式主动悬架系统、馈能式被动悬架系统和最大馈能系统的馈能特性。结果表明:被动悬架系统在馈能特性上优于主动系统。
3) 比较分析了B、C级路面下馈能式悬架系统的馈能特性。结果表明:馈能式悬架系统的各项馈能量受路面激励的影响较大,而馈能效率受路面激励的影响相对较小。
4) 电容对馈能系统的馈能特性有一定的影响。馈能系统在开始启动工作时,由于电容的电压没有达到额定值,此时系统的馈能量较低。在该时间段内,馈能式主动悬架系统反馈的能量小于消耗的能量,系统需要外部供能。而在整个时间历程上来看,馈能式主动系统可以实现自供能。
 2013, Vol. 36
2013, Vol. 36


